Structures de données exotiques: Merkle modifiée Patricia Trie

"Quel genre de diable devrais-je me souvenir par cœur de tous ces fichus algorithmes et structures de données?"

À ce sujet se résume aux commentaires de la plupart des articles sur le passage des entretiens techniques. La thèse principale, en règle générale, est que tout ce qui est utilisé d'une manière ou d'une autre a déjà été mis en œuvre dix fois et il est très peu probable que ce programmeur ordinaire doive y faire face. Eh bien, dans une certaine mesure, cela est vrai. Mais, il s'est avéré que tout n'était pas implémenté, et moi, malheureusement (ou heureusement?), Je devais encore créer une structure de données.

Mystérieuse Merkle modifiée Patricia Trie.

Puisqu'il n'y a aucune information sur cet arbre sur le habr et sur le milieu - un peu plus, je veux vous dire de quel type d'animal il s'agit et avec quoi il est mangé.

Qu'est ce que c'est

Avertissement: la principale source d'informations pour la mise en œuvre pour moi était le papier jaune , ainsi que les codes source parity-ethereum et go-ethereum . Il y avait un minimum d'informations théoriques sur la justification de certaines décisions, donc toutes les conclusions sur les raisons de prendre certaines décisions m'appartiennent. Au cas où je me tromperais sur quelque chose - je serai heureux des corrections dans les commentaires.

Un arbre est une structure de données qui est un graphe acyclique connecté. Ici, tout est simple, tout le monde le sait.

L'arbre des préfixes est l'arbre racine dans lequel les paires clé-valeur peuvent être stockées car les nœuds sont divisés en deux types: ceux qui contiennent une partie du chemin (préfixe) et les nœuds feuilles qui contiennent la valeur stockée. Une valeur est présente dans un arbre si et seulement si, à l'aide de la clé, nous pouvons aller jusqu'à la racine de l'arbre et trouver un nœud avec une valeur à la fin.

L'arbre PATRICIA est un arbre de préfixe dans lequel les préfixes sont binaires - c'est-à-dire que chaque nœud clé stocke des informations sur un bit.

L' arbre Merkle est un arbre de hachage construit sur une sorte de chaîne de données, agrégeant ces mêmes hachages en un seul (racine), stockant des informations sur l'état de tous les blocs de données. Autrement dit, le hachage racine est une sorte de "signature numérique" de l'état de la chaîne de blocs. Cette chose est utilisée activement dans la blockchain, et plus d'informations à ce sujet peuvent être trouvées ici .

Total: Merkle modifié Patricia Trie (ci-après MPT pour faire court) est un arbre de hachage qui stocke les paires clé-valeur, et les clés sont présentées sous forme binaire. Et en quoi consiste exactement «Modifié», nous le découvrirons un peu plus tard lorsque nous discuterons de l'implémentation.

Pourquoi ça?

MPT est utilisé dans le projet Ethereum pour stocker des données sur les comptes, les transactions, les résultats de leur exécution et d'autres données nécessaires au fonctionnement du système.
Contrairement au Bitcoin, dans lequel l'état est implicite et est calculé par chaque nœud indépendamment, le solde de chaque compte (ainsi que les données qui lui sont associées) sont stockés directement sur la blockchain en direct. De plus, l'emplacement et l'immuabilité des données doivent être fournis cryptographiquement - peu de gens utiliseront la crypto-monnaie dans laquelle le solde d'un compte aléatoire peut changer sans raisons objectives.

Le principal problème rencontré par les développeurs d'Ethereum est la création d'une structure de données capable de stocker efficacement des paires clé-valeur et en même temps de vérifier les données stockées. Alors MPT est apparu.

Comment est-ce?

MPT est un arbre de préfixe PATRICIA dans lequel les clés sont des séquences d'octets.

Les bords de cet arbre sont des séquences de quartets (demi-octets). En conséquence, un nœud peut avoir jusqu'à seize descendants (correspondant aux branches de 0x0 à 0xF).

Les nœuds sont divisés en 3 types:

• Noeud de branche. Le nœud utilisé pour la ramification. Contient jusqu'à 1 à 16 liens vers des nœuds enfants. Peut également contenir une valeur.
• Noeud d'extension. Un nœud auxiliaire qui stocke une partie du chemin commun à plusieurs nœuds enfants, ainsi qu'un lien vers le nœud de branche, qui se trouve ci-dessous.
• Nœud foliaire. Un nœud contenant une partie du chemin et la valeur stockée. C'est la fin de la chaîne.

Comme déjà mentionné, MPT est construit au-dessus d'un autre référentiel kv, qui stocke les nœuds sous la forme de "lien" => "nœud codé RLP ".

Et nous arrivons ici avec un nouveau concept: RLP. En bref, il s'agit d'une méthode de codage de données représentant des listes ou des séquences d'octets. Exemple: [ "cat", "dog" ] = [ 0xc8, 0x83, 'c', 'a', 't', 0x83, 'd', 'o', 'g' ] . Je n'entrerai pas dans les détails en particulier, et dans la mise en œuvre, j'utilise une bibliothèque prête à l'emploi, car la couverture de ce sujet gonflera également un article déjà assez volumineux. Si vous êtes toujours intéressé, vous pouvez en savoir plus ici . Nous nous limitons au fait que nous pouvons encoder des données en RLP et les décoder à nouveau.

Un lien vers un nœud est défini comme suit: si la longueur du nœud codé RLP est de 32 octets ou plus, alors le lien est un hachage keccak de la représentation RLP du nœud. Si la longueur est inférieure à 32 octets, le lien est la représentation RLP du nœud lui-même.

De toute évidence, dans le deuxième cas, vous n'avez pas besoin d'enregistrer le nœud dans la base de données, car il sera entièrement enregistré dans le nœud parent.

La combinaison de trois types de nœuds vous permet de stocker efficacement des données dans le cas où il y a peu de clés (alors la plupart des chemins seront stockés dans les nœuds d'extension et de feuille, et il y aura peu de nœuds de branche), et dans le cas où il y a beaucoup de nœuds (les chemins ne seront pas stockés explicitement, mais ils "se rassembleront" pendant le passage à travers des nœuds de branche).

Un exemple complet d'arbre utilisant toutes sortes de nœuds:

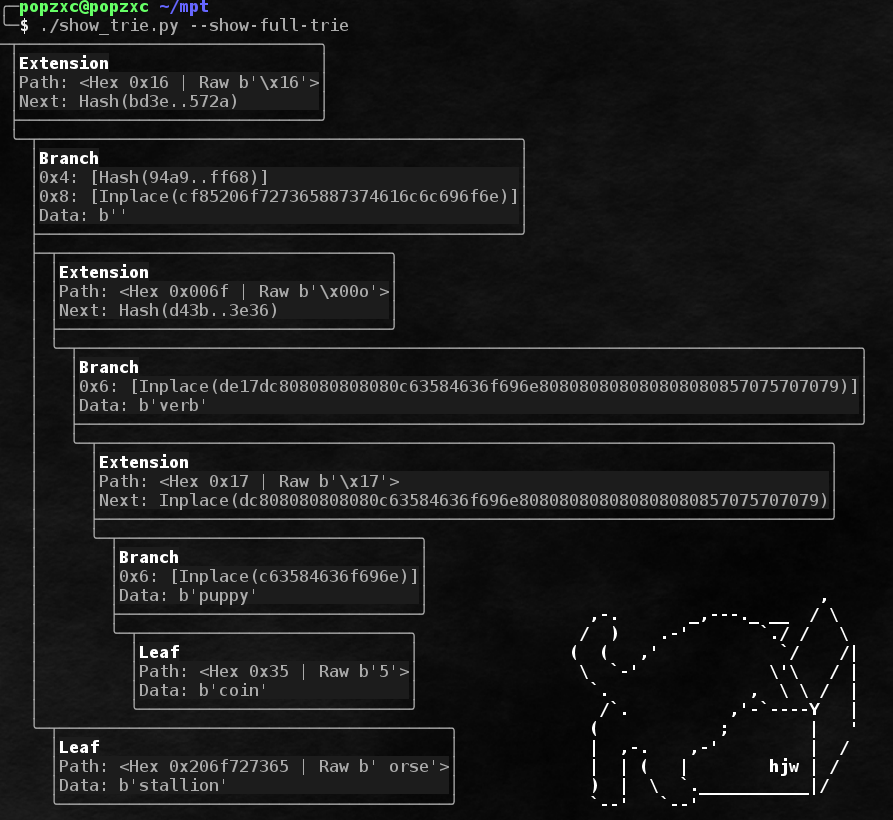
Comme vous l'avez peut-être remarqué, les parties stockées des chemins sont préfixées. Les préfixes sont nécessaires à plusieurs fins:

1. Distinguer les nœuds d'extension des nœuds feuilles.
2. Pour aligner des séquences d'un nombre impair de grignotages.

Les règles de création des préfixes sont très simples:

• Le préfixe prend 1 quartet. Si la longueur du chemin (à l'exclusion du préfixe) est impaire, le chemin commence immédiatement après le préfixe. Si la longueur du chemin est pair, pour aligner après le préfixe, le quartet 0x0 est ajouté en premier.
• Le préfixe est initialement 0x0.
• Si la longueur du chemin est impaire, alors 0x1 est ajouté au préfixe, si pair - 0x0.
• Si le chemin mène à un nœud Leaf, 0x2 est ajouté au préfixe, si 0x0 est ajouté au nœud Extension.

Sur les beatiks, je pense que ce sera plus clair:

 0b0000 =>  , Extension  0b0001 =>  , Extension  0b0010 =>  , Leaf  0b0011 =>  , Leaf  

Suppression qui n'est pas une suppression

Malgré le fait que l'arborescence ait pour effet de supprimer des nœuds, en fait, tout ce qui a été ajouté une fois reste dans l'arborescence pour toujours.

Cela est nécessaire pour ne pas créer une arborescence complète pour chaque bloc, mais pour ne stocker que la différence entre l'ancienne et la nouvelle version de l'arborescence.

Par conséquent, en utilisant différents hachages racine comme point d'entrée, nous pouvons obtenir l'un des états dans lesquels l'arbre a déjà été.

Ce ne sont pas toutes des optimisations. Il y a plus, mais nous n'en parlerons pas - et donc l'article est volumineux. Cependant, vous pouvez lire par vous-même.

Implémentation

La théorie est terminée, passons à la pratique. Nous utiliserons la lingua franca du monde informatique, c'est-à-dire le python .

Puisqu'il y aura beaucoup de code, et pour le format de l'article beaucoup devra être réduit et divisé, je laisserai immédiatement un lien vers github .
Si nécessaire, vous pouvez voir l'image entière.

Tout d'abord, nous définissons l'interface d'arbre que nous voulons obtenir en conséquence:

 class MerklePatriciaTrie: def __init__(self, storage, root=None): pass def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass 

L'interface est extrêmement simple. Les opérations disponibles sont l'obtention, la suppression, l'insertion et la modification (combinées dans la mise à jour), ainsi que l'obtention du hachage racine.

Le stockage sera transféré à la méthode __init__ - une structure de données de type dict dans laquelle nous __init__ les nœuds, ainsi que la root - le "sommet" de l'arborescence. Si None est passé en tant que root , nous supposons que l'arborescence est vide et fonctionne à partir de zéro.

_Remarque: vous vous demandez peut-être pourquoi les variables dans les méthodes sont nommées en tant que encoded_key et encoded_value , et pas seulement key / value . La réponse est simple: selon la spécification, toutes les clés et valeurs doivent être encodées en RLP . Nous ne nous en préoccuperons pas et laisserons cette occupation sur les épaules des utilisateurs de la bibliothèque._

Cependant, avant de commencer à implémenter l'arbre lui-même, deux choses importantes doivent être faites:

1. Implémentez la classe NibblePath , qui est une chaîne de grignotages, afin de ne pas les coder manuellement.
2. Pour implémenter la classe Node dans le cadre de cette classe - Extension , Leaf et Branch .

Nibblepath

Alors, NibblePath . Puisque nous nous déplacerons activement dans l'arborescence, la base de la fonctionnalité de notre classe devrait être la possibilité de définir le "décalage" depuis le début du chemin, ainsi que de recevoir un quartet spécifique. Sachant cela, nous définissons la base de notre classe (ainsi que quelques constantes utiles pour travailler avec les préfixes ci-dessous):

 class NibblePath: ODD_FLAG = 0x10 LEAF_FLAG = 0x20 def __init__(self, data, offset=0): self._data = data # ,   . self._offset = offset #      def consume(self, amount): # "" N      . self._offset += amount return self def at(self, idx): #      idx = idx + self._offset #    ,   ,    , #   ,    -      . byte_idx = idx // 2 nibble_idx = idx % 2 #   . byte = self._data[byte_idx] #      . nibble = byte >> 4 if nibble_idx == 0 else byte & 0x0F return nibble 

C'est assez simple, non?

Il ne reste plus qu'à écrire des fonctions d'encodage et de décodage d'une séquence de quartets.

 class NibblePath: # ... def decode_with_type(data): #   : # ,     ,    . is_odd_len = data[0] & NibblePath.ODD_FLAG == NibblePath.ODD_FLAG is_leaf = data[0] & NibblePath.LEAF_FLAG == NibblePath.LEAF_FLAG #    ,     #    . offset  , #       "" . offset = 1 if is_odd_len else 2 return NibblePath(data, offset), is_leaf def encode(self, is_leaf): output = [] #    ,       . nibbles_len = len(self._data) * 2 - self._offset is_odd = nibbles_len % 2 == 1 #  . prefix = 0x00 #    ,    . #      (self.at(0))     . #           (0x0). prefix += self.ODD_FLAG + self.at(0) if is_odd else 0x00 #  ,  Leaf node,  . prefix += self.LEAF_FLAG if is_leaf else 0x00 output.append(prefix) # ,      ,  . pos = nibbles_len % 2 #          , #     2 ,    , #     , #    . while pos < nibbles_len: byte = self.at(pos) * 16 + self.at(pos + 1) output.append(byte) pos += 2 return bytes(output) 

En principe, c'est le minimum nécessaire pour un travail pratique avec des amuse-gueules. Bien sûr, dans l'implémentation actuelle, il existe encore un certain nombre de méthodes auxiliaires (telles que combine , fusionner deux chemins en un seul), mais leur implémentation est très triviale. Si vous êtes intéressé, la version complète peut être trouvée ici .

Noeud

Comme nous le savons déjà, nos nœuds sont divisés en trois types: Leaf, Extension et Branch. Tous peuvent être encodés et décodés, et la seule différence réside dans les données stockées à l'intérieur. Pour être honnête, c'est ce que les types de données algébriques sont demandés, et dans Rust , par exemple, j'écrirais quelque chose dans l'esprit:

 pub enum Node<'a> { Leaf(NibblesSlice<'a>, &'a [u8]), Extension(NibblesSlice<'a>, NodeReference), Branch([Option<NodeReference>; 16], Option<&'a [u8]>), } 

Cependant, il n'y a pas d'ADT en python en tant que tel, nous allons donc définir la classe Node , et à l'intérieur, il y a trois classes correspondant aux types de nœuds. Nous implémentons le codage directement dans les classes de nœuds et le décodage dans la classe de Node .

La mise en œuvre est cependant élémentaire:

Feuille:

 class Leaf: def __init__(self, path, data): self.path = path self.data = data def encode(self): #    --    , #   -  ,   -  . return rlp.encode([self.path.encode(True), self.data]) 

Extension:

 class Extension: def __init__(self, path, next_ref): self.path = path self.next_ref = next_ref def encode(self): #    --    , #   -  ,   -    . next_ref = _prepare_reference_for_encoding(self.next_ref) return rlp.encode([self.path.encode(False), next_ref]) 

Succursale:

 class Branch: def __init__(self, branches, data=None): self.branches = branches self.data = data def encode(self): #    --    ,  #  16 -     (  ), #   -   (  ). branches = list(map(_prepare_reference_for_encoding, self.branches)) return rlp.encode(branches + [self.data]) 

Tout est très simple. La seule chose qui peut poser des questions est la fonction _prepare_reference_for_encoding .

Ensuite, je l'avoue, j'ai dû utiliser une petite béquille. Le fait est que la bibliothèque rlp décode les données de manière récursive, et le lien vers un autre nœud, comme nous le savons, peut être des données rlp (dans le cas où le nœud codé fait moins de 32 caractères). Travailler avec des liens dans deux formats - octets de hachage et nœud décodé - est très gênant. Par conséquent, j'ai écrit deux fonctions qui, après décodage du nœud, renvoient les liens au format octet, et les décodent si nécessaire, avant d'enregistrer. Ces fonctions sont:

 def _prepare_reference_for_encoding(ref): #    ( ,   ) --  . #       :) if 0 < len(ref) < 32: return rlp.decode(ref) return ref def _prepare_reference_for_usage(ref): #     -   . #          . if isinstance(ref, list): return rlp.encode(ref) return ref 

Terminez avec les nœuds en écrivant une classe Node . Il n'y aura que 2 méthodes: décoder le nœud et transformer le nœud en lien.

 class Node: # class Leaf(...) # class Extension(...) # class Branch(...) def decode(encoded_data): data = rlp.decode(encoded_data) # 17  -  Branch . if len(data) == 17: branches = list(map(_prepare_reference_for_usage, data[:16])) node_data = data[16] return Node.Branch(branches, node_data) #    17,   2.   - . #      ,     . path, is_leaf = NibblePath.decode_with_type(data[0]) if is_leaf: return Node.Leaf(path, data[1]) else: ref = _prepare_reference_for_usage(data[1]) return Node.Extension(path, ref) def into_reference(node): #    . #      32 , #   -   . #       . encoded_node = node.encode() if len(encoded_node) < 32: return encoded_node else: return keccak_hash(encoded_node) 

Une pause

Fuh! Il y a beaucoup d'informations. Je pense qu'il est temps de se détendre. Voici un autre chat pour vous:

Milota, c'est ça? Bon, revenons à nos arbres.

MerklePatriciaTrie

Hourra - les éléments auxiliaires sont prêts, nous passons aux plus délicieux. Au cas où, je rappellerai l'interface de notre arbre. Dans le même temps, nous implémentons la méthode __init__ .

 class MerklePatriciaTrie: def __init__(self, storage, root=None): self._storage = storage self._root = root def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass 

Mais avec les méthodes restantes, nous traiterons un par un.

obtenir

La méthode get (comme, en principe, les autres méthodes) comprendra deux parties. La méthode elle-même préparera les données et amènera le résultat à la forme attendue, tandis que le vrai travail se fera à l'intérieur de la méthode auxiliaire.

La méthode de base est extrêmement simple:

 class MerklePatriciaTrie: # ... def get(self, encoded_key): if not self._root: raise KeyError path = NibblePath(encoded_key) #       #  ,    ,    . result_node = self._get(self._root, path) if type(result_node) is Node.Extension or len(result_node.data) == 0: raise KeyError return result_node.data 

Cependant, _get pas beaucoup plus compliqué: pour arriver au nœud souhaité, nous devons aller de la racine à l'ensemble du chemin fourni. Si à la fin nous avons trouvé un nœud avec des données (feuille ou branche) - hourra, les données sont reçues. S'il n'a pas été possible de passer, la clé requise est manquante dans l'arborescence.

Réalisation:

 class MerklePatriciaTrie: # ... def _get(self, node_ref, path): #      . node = self._get_node(node_ref) #    --   . #   ,      . if len(path) == 0: return node if type(node) is Node.Leaf: #     Leaf-,     , #      . if node.path == path: return node elif type(node) is Node.Extension: #    -- Extension,    . if path.starts_with(node.path): rest_path = path.consume(len(node.path)) return self._get(node.next_ref, rest_path) elif type(node) is Node.Branch: #    -- Branch,     . #   ,           #  :      . branch = node.branches[path.at(0)] if len(branch) > 0: return self._get(branch, path.consume(1)) #    ,        , #     . raise KeyError 

Eh bien, en même temps, nous écrirons des méthodes pour sauvegarder et charger des nœuds. Ils sont simples:

 class MerklePatriciaTrie: # ... def _get_node(self, node_ref): raw_node = None if len(node_ref) == 32: raw_node = self._storage[node_ref] else: raw_node = node_ref return Node.decode(raw_node) def _store_node(self, node): reference = Node.into_reference(node) if len(reference) == 32: self._storage[reference] = node.encode() return reference 

mettre à jour

La méthode de update est déjà plus intéressante. Il suffit d'aller jusqu'au bout et d'insérer le nœud Feuille ne fonctionnera pas toujours. Il est probable que le point de séparation des clés se trouve quelque part à l'intérieur du nœud Feuille ou Extension déjà enregistré. Dans ce cas, vous devrez les séparer et créer plusieurs nouveaux nœuds.

En général, toute la logique peut être décrite par les règles suivantes:

1. Alors que le chemin coïncide entièrement avec les nœuds existants, nous descendons récursivement l'arbre.
2. Si le chemin est terminé et que nous sommes dans le nœud Branche ou Feuille, cela signifie que la update met simplement à jour la valeur correspondant à cette clé.
3. Si les chemins sont divisés (c'est-à-dire que nous ne mettons pas à jour la valeur, mais en insérons une nouvelle), et que nous sommes dans le nœud Branche, créez un nœud Feuille et spécifiez un lien vers celui-ci dans la branche de branche branche correspondante.
4. Si les chemins sont divisés et que nous sommes dans le nœud Feuille ou Extension, nous devons créer un nœud Branche qui sépare les chemins et, si nécessaire, un nœud Extension pour la partie commune du chemin.

Exprimons progressivement cela dans le code. Pourquoi progressivement? Parce que la méthode est volumineuse et il sera difficile de la comprendre en vrac.
Cependant, je vais laisser un lien vers la méthode complète ici .

 class MerklePatriciaTrie: # ... def update(self, encoded_key, encoded_value): path = NibblePath(encoded_key) result = self._update(self._root, path, encoded_value) self._root = result def _update(self, node_ref, path, value): #       (,   ), #       . if not node_ref: return self._store_node(Node.Leaf(path, value)) #          #    . node = self._get_node(node_ref) if type(node) == Node.Leaf: ... elif type(node) == Node.Extension: ... elif type(node) == Node.Branch: ... 

Il n'y a pas assez de logique générale, le plus intéressant est à l'intérieur if art.

if type(node) == Node.Leaf

Voyons d'abord les nœuds Leaf. Seuls 2 scénarios sont possibles avec eux:

1. Le reste du chemin que nous suivons est exactement le même que le chemin stocké dans le nœud Feuille. Dans ce cas, il suffit de modifier la valeur, d'enregistrer le nouveau nœud et de lui renvoyer un lien.

   
   

2. Les chemins sont différents.
   Dans ce cas, vous devez créer un nœud de branche qui sépare les deux chemins.
   Si l'un des chemins est vide, sa valeur sera transférée directement au nœud de branche.
   Sinon, il faudra créer deux nœuds Leaf raccourcis de la longueur de la partie commune des chemins + 1 quartet (ce quartet sera indiqué par l'index de la branche correspondante du nœud Branch).

   
   

Vous devrez également vérifier s'il existe une partie commune du chemin afin de comprendre si nous devons également créer un nœud d'extension.

Dans le code, cela ressemblera à ceci:

 if type(node) == Node.Leaf: if node.path == path: #  .       . node.data = value return self._store_node(node) #    . #    . common_prefix = path.common_prefix(node.path) #      . path.consume(len(common_prefix)) node.path.consume(len(common_prefix)) #  Branch . branch_reference = self._create_branch_node(path, value, node.path, node.data) # ,    Extension-. if len(common_prefix) != 0: return self._store_node(Node.Extension(common_prefix, branch_reference)) else: return branch_reference 

La procédure _create_branch_node est la suivante:

 def _create_branch_node(self, path_a, value_a, path_b, value_b): #    Branch-. branches = [b''] * 16 # ,     Branch- . branch_value = b'' if len(path_a) == 0: branch_value = value_a elif len(path_b) == 0: branch_value = value_b #    Leaf-,  . self._create_branch_leaf(path_a, value_a, branches) self._create_branch_leaf(path_b, value_b, branches) #  Branch-     . return self._store_node(Node.Branch(branches, branch_value)) def _create_branch_leaf(self, path, value, branches): # ,     Leaf-. if len(path) > 0: #    ( ). idx = path.at(0) #  Leaf-   ,     . leaf_ref = self._store_node(Node.Leaf(path.consume(1), value)) branches[idx] = leaf_ref 

if type(node) == Node.Extension

Dans le cas du nœud Extension, tout ressemble à un nœud Leaf.

1. Si le chemin du nœud Extension est un préfixe pour notre chemin, nous allons simplement de manière récursive.

   
   

2. Sinon, nous devons faire la séparation en utilisant le nœud Branch, comme dans le cas décrit ci-dessus.

   
   

En conséquence, le code:

 elif type(node) == Node.Extension: if path.starts_with(node.path): #         . new_reference = \ self._update(node.next_ref, path.consume(len(node.path)), value) return self._store_node(Node.Extension(node.path, new_reference)) #  Extension-. #     . common_prefix = path.common_prefix(node.path) #  . path.consume(len(common_prefix)) node.path.consume(len(common_prefix)) #  Branch- ,  ,    . branches = [b''] * 16 branch_value = value if len(path) == 0 else b'' #     Leaf-  Extension- . self._create_branch_leaf(path, value, branches) self._create_branch_extension(node.path, node.next_ref, branches) branch_reference = self._store_node(Node.Branch(branches, branch_value)) # ,    Extension-. if len(common_prefix) != 0: return self._store_node(Node.Extension(common_prefix, branch_reference)) else: return branch_reference 

La procédure _create_branch_extension logiquement équivalente à la procédure _create_branch_leaf , mais fonctionne avec le nœud Extension.

if type(node) == Node.Branch

Mais avec le nœud Branch, tout est simple. Si le chemin est vide, nous enregistrons simplement la nouvelle valeur dans le nœud Branch actuel. Si le chemin n'est pas vide, nous en «mordons» un quartet et descendons récursivement.

Le code, je pense, n'a pas besoin de commentaires.

 elif type(node) == Node.Branch: if len(path) == 0: return self._store_node(Node.Branch(node.branches, value)) idx = path.at(0) new_reference = self._update(node.branches[idx], path.consume(1), value) node.branches[idx] = new_reference return self._store_node(node) 

effacer

Fuh! La dernière méthode reste. Il est le plus gai. La complexité de la suppression est que nous devons remettre la structure dans l'état dans lequel elle serait tombée si nous avions fait toute la chaîne de update , à l'exclusion uniquement de la clé supprimée.

Ceci est extrêmement important, car sinon une situation est possible dans laquelle le hachage racine différera pour deux arbres contenant les mêmes données. Et une telle «fonctionnalité», comme vous le comprenez, effacera tout le sens de cette structure de données.

Cette exigence donne lieu à un assez grand nombre de scénarios d'action possibles. De plus, la fonction au N-ème niveau d'imbrication après suppression directe devra savoir ce qui s'est passé au niveau N + 1. Pour ce faire, nous allons introduire une énumération supplémentaire - DeleteActionque nous reviendrons en haut.

Le cadre de la méthode deleteressemblera à ceci:

 class MerklePatriciaTrie: # ... # Enum, ,         . class _DeleteAction(Enum): #    . #     , #        (_DeleteAction, None). DELETED = 1, #    (,    ). #     ,    #    : (_DeleteAction, ___). UPDATED = 2, #    Branch-  .   -- #    : # (_DeleteAction, (___, ___)) USELESS_BRANCH = 3 def delete(self, encoded_key): if self._root is None: return path = NibblePath(encoded_key) action, info = self._delete(self._root, path) if action == MerklePatriciaTrie._DeleteAction.DELETED: #   . self._root = None elif action == MerklePatriciaTrie._DeleteAction.UPDATED: #   . new_root = info self._root = new_root elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #   . _, new_root = info self._root = new_root def _delete(self, node_ref, path): node = self._get_node(node_ref) if type(node) == Node.Leaf: pass elif type(node) == Node.Extension: pass elif type(node) == Node.Branch: pass 

, get update . . .

if type(node) == Node.Leaf

. . — , , .

:

 if type(node) == Node.Leaf: if path == node.path: return MerklePatriciaTrie._DeleteAction.DELETED, None else: raise KeyError 

, "" — . , . .

if type(node) == Node.Extension

C Extension- :

1. , Extension- . — .
2. _delete , "" .
3. . :

• . .
• . .
• Branch-. . , Branch- . , , Leaf-. — Extension-.

:

 elif type(node) == Node.Extension: if not path.starts_with(node.path): raise KeyError #   . #       . action, info = self._delete(node.next_ref, path.consume(len(node.path))) if action == MerklePatriciaTrie._DeleteAction.DELETED: return action, None elif action == MerklePatriciaTrie._DeleteAction.UPDATED: #    ,     . child_ref = info new_ref = self._store_node(Node.Extension(node.path, child_ref)) return action, new_ref elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #     Branch-. stored_path, stored_ref = info # ,     Branch-. child = self._get_node(stored_ref) new_node = None if type(child) == Node.Leaf: #  branch-  . #     Leaf-  Extension. path = NibblePath.combine(node.path, child.path) new_node = Node.Leaf(path, child.data) elif type(child) == Node.Extension: #  Branch-  Extension-. #       . path = NibblePath.combine(node.path, child.path) new_node = Node.Extension(path, child.next_ref) elif type(child) == Node.Branch: #  Branch-      Branch-. #    Extension-    . path = NibblePath.combine(node.path, stored_path) new_node = Node.Extension(path, stored_ref) new_reference = self._store_node(new_node) return MerklePatriciaTrie._DeleteAction.UPDATED, new_reference 

if type(node) == Node.Branch

.

, . Branch-, …

Pourquoi? Branch- Leaf- ( ) Extension- ( ).
, . , — Leaf-. — Extension-. , , 2 — Branch- .

? :

:

1. , .
2. , _delete .

:

 elif type(node) == Node.Branch: action = None idx = None info = None if len(path) == 0 and len(node.data) == 0: raise KeyError elif len(path) == 0 and len(node.data) != 0: node.data = b'' action = MerklePatriciaTrie._DeleteAction.DELETED else: #   ,    . #    . idx = path.at(0) if len(node.branches[idx]) == 0: raise KeyError action, info = self._delete(node.branches[idx], path.consume(1)) #  ,   ,  . #      -    #    . node.branches[idx] = b'' 

_DeleteAction .

1. Branch- , ( , ). .

 if action == MerklePatriciaTrie._DeleteAction.UPDATED: #   . next_ref = info node.branches[idx] = next_ref reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #    . _, next_ref = info node.branches[idx] = next_ref reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference 

1. ( , ), , .

. :

• . , , , . , .
• , . Leaf- . .
• , . , , .
• , , Branch- . , _DeleteAction — UPDATED .

 if action == MerklePatriciaTrie._DeleteAction.DELETED: non_empty_count = sum(map(lambda x: 1 if len(x) > 0 else 0, node.branches)) if non_empty_count == 0 and len(node.data) == 0: # Branch- ,  . return MerklePatriciaTrie._DeleteAction.DELETED, None elif non_empty_count == 0 and len(node.data) != 0: #  ,   . path = NibblePath([]) reference = self._store_node(Node.Leaf(path, node.data)) return MerklePatriciaTrie._DeleteAction.USELESS_BRANCH, (path, reference) elif non_empty_count == 1 and len(node.data) == 0: #  ,   . return self._build_new_node_from_last_branch(node.branches) else: #  1+   ,  2+ . # Branch-  ,   - UPDATED. reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference 

_build_new_node_from_last_branch .

— Leaf Extension, , .

— Branch, Extension , , Branch.

 def _build_new_node_from_last_branch(self, branches): #    . idx = 0 for i in range(len(branches)): if len(branches[i]) > 0: idx = i break #     . prefix_nibble = NibblePath([idx], offset=1) #     child = self._get_node(branches[idx]) path = None node = None #   . if type(child) == Node.Leaf: path = NibblePath.combine(prefix_nibble, child.path) node = Node.Leaf(path, child.data) elif type(child) == Node.Extension: path = NibblePath.combine(prefix_nibble, child.path) node = Node.Extension(path, child.next_ref) elif type(child) == Node.Branch: path = prefix_nibble node = Node.Extension(path, branches[idx]) #  . reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.USELESS_BRANCH, (path, reference) 

Le reste

. , … root .

Ici:

 class MerklePatriciaTrie: # ... def root(self): return self._root 

, .

… . , , Ethereum . , , , . , :)

, , pip install -U eth_mpt — .

Résultats

?

, -, , - , , . — , .

-, , , — . , skip list interval tree, — , , .

-, , . , - .

-, — .

, , — !

: 1 , 2 , 3 . ! , .