Nous avons déjà discuté du
moteur d'indexation PostgreSQL, de
l'interface des méthodes d'accès et de trois méthodes: l'
index de hachage , l'
arborescence B et
GiST . Dans cet article, nous décrirons SP-GiST.
SP-GiST
Tout d'abord, quelques mots sur ce nom. La partie "GiST" fait allusion à une certaine similitude avec la méthode d'accès du même nom. La similitude existe: les deux sont des arbres de recherche généralisés qui fournissent un cadre pour la construction de diverses méthodes d'accès.
"SP" signifie partitionnement d'espace. L'espace ici est souvent juste ce que nous appelons un espace, par exemple un plan à deux dimensions. Mais nous verrons que tout espace de recherche est destiné, c'est-à-dire en fait n'importe quel domaine de valeur.
SP-GiST convient aux structures où l'espace peut être récursivement divisé en zones
sans intersection . Cette classe comprend les arbres quadruples, les arbres k-dimensionnels (arbres kD) et les arbres radix.
La structure
Ainsi, l'idée de la méthode d'accès SP-GiST est de diviser le domaine de valeur en
sous- domaines
non chevauchants, chacun pouvant à son tour également être divisé. Le partitionnement comme celui-ci induit
des arbres
non équilibrés (contrairement aux arbres B et au GiST standard).
Le fait de ne pas se croiser simplifie la prise de décision lors de l'insertion et de la recherche. En revanche, en règle générale, les arbres induits sont de faible ramification. Par exemple, un nœud d'un arbre quadruple a généralement quatre nœuds enfants (contrairement aux arbres B, où les nœuds s'élèvent à des centaines) et une plus grande profondeur. De tels arbres conviennent bien au travail en RAM, mais l'index est stocké sur un disque et, par conséquent, pour réduire le nombre d'opérations d'E / S, les nœuds doivent être regroupés dans des pages, et il n'est pas facile de le faire efficacement. En outre, le temps qu'il faut pour trouver différentes valeurs dans l'index peut varier en raison des différences de profondeur de branche.
Cette méthode d'accès, de la même manière que GiST, prend en charge les tâches de bas niveau (accès et verrous simultanés, journalisation et algorithme de recherche pur) et fournit une interface simplifiée spécialisée pour permettre l'ajout de la prise en charge de nouveaux types de données et de nouveaux algorithmes de partitionnement.
Un nœud interne de l'arborescence SP-GiST stocke les références aux nœuds enfants; une
étiquette peut être définie pour chaque référence. De plus, un nœud interne peut stocker une valeur appelée
préfixe . En fait, cette valeur n'est pas obligatoire un préfixe; il peut être considéré comme un prédicat arbitraire respecté pour tous les nœuds enfants.
Les nœuds feuilles de SP-GiST contiennent une valeur de type indexé et une référence à une ligne de table (TID). Les données indexées elles-mêmes (clé de recherche) peuvent être utilisées comme valeur, mais ne sont pas obligatoires: une valeur raccourcie peut être stockée.
De plus, les nœuds feuilles peuvent être regroupés dans des listes. Ainsi, un nœud interne peut référencer non seulement une valeur, mais une liste entière.
Notez que les préfixes, les étiquettes et les valeurs dans les nœuds terminaux ont leurs propres types de données, indépendants les uns des autres.
De la même manière que dans GiST, la fonction principale à définir pour la recherche est
la fonction de cohérence . Cette fonction est appelée pour un nœud d'arbre et renvoie un ensemble de nœuds enfants dont les valeurs "sont cohérentes" avec le prédicat de recherche (comme d'habitude, sous la forme "
expression d'opérateur de champ indexé "). Pour un nœud feuille, la fonction de cohérence détermine si la valeur indexée dans ce nœud correspond au prédicat de recherche.
La recherche commence par le nœud racine. La fonction de cohérence permet de savoir quels nœuds enfants il est logique de visiter. L'algorithme se répète pour chacun des nœuds trouvés. La recherche est la profondeur d'abord.
Au niveau physique, les nœuds d'index sont regroupés dans des pages pour rendre le travail avec les nœuds efficace du point de vue des opérations d'E / S. Notez qu'une page peut contenir des nœuds internes ou terminaux, mais pas les deux.
Exemple: quadtree
Un quadtree est utilisé pour indexer des points dans un plan. Une idée est de diviser récursivement les zones en quatre parties (quadrants) par rapport au
point central . La profondeur des branches dans un tel arbre peut varier et dépend de la densité des points dans les quadrants appropriés.
Voilà à quoi cela ressemble en chiffres, par exemple de la
base de données de démonstration augmentée par les aéroports du site
openflights.org . Soit dit en passant, nous avons récemment publié une nouvelle version de la base de données dans laquelle, parmi les autres, nous avons remplacé la longitude et la latitude par un champ de type "point".
Tout d'abord, nous avons divisé l'avion en quatre quadrants ...
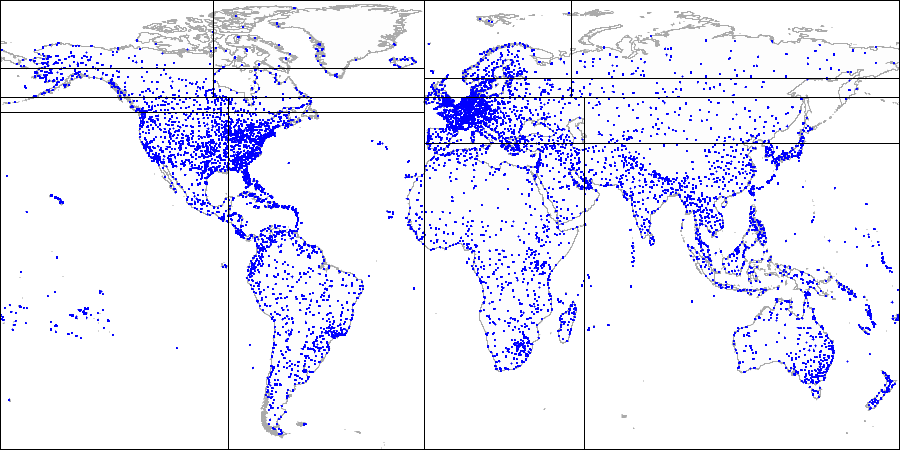Ensuite, nous avons divisé chacun des quadrants ...
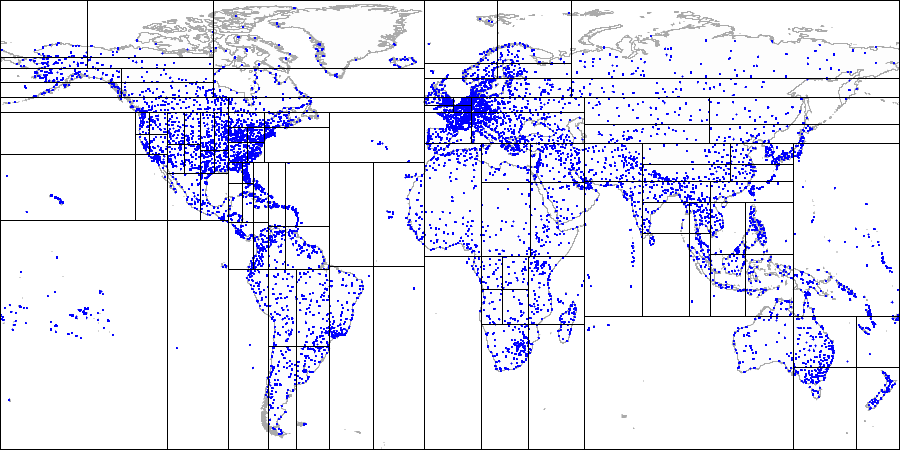Et ainsi de suite jusqu'à ce que nous obtenions le partitionnement final.Fournissons plus de détails sur un exemple simple que nous avons déjà considéré dans l'
article lié à GiST . Voyez à quoi le partitionnement peut ressembler dans ce cas:
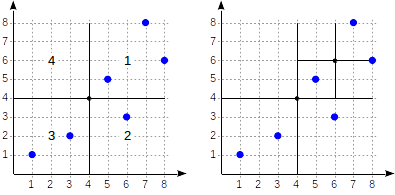
Les quadrants sont numérotés comme indiqué sur la première figure. Par souci de clarté, plaçons les nœuds enfants de gauche à droite exactement dans la même séquence. Une structure d'index possible dans ce cas est illustrée dans la figure ci-dessous. Chaque nœud interne fait référence à un maximum de quatre nœuds enfants. Chaque référence peut être étiquetée avec le numéro du quadrant, comme sur la figure. Mais il n'y a pas d'étiquette dans l'implémentation car il est plus pratique de stocker un tableau fixe de quatre références dont certaines peuvent être vides.
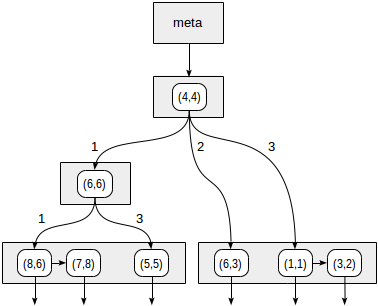
Les points qui se trouvent sur les limites se rapportent au quadrant avec le plus petit nombre.
postgres=# create table points(p point); postgres=# insert into points(p) values (point '(1,1)'), (point '(3,2)'), (point '(6,3)'), (point '(5,5)'), (point '(7,8)'), (point '(8,6)'); postgres=# create index points_quad_idx on points using spgist(p);
Dans ce cas, la classe d'opérateur "quad_point_ops" est utilisée par défaut, qui contient les opérateurs suivants:
postgres=# select amop.amopopr::regoperator, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'quad_point_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'spgist' and amop.amoplefttype = opc.opcintype;
amopopr | amopstrategy -----------------+-------------- <<(point,point) | 1 strictly left >>(point,point) | 5 strictly right ~=(point,point) | 6 coincides <^(point,point) | 10 strictly below >^(point,point) | 11 strictly above <@(point,box) | 8 contained in rectangle (6 rows)
Par exemple, regardons comment la requête
select * from points where p >^ point '(2,7)' sera exécuté (trouver tous les points qui se trouvent au-dessus de celui donné).
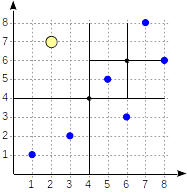
Nous commençons par le nœud racine et utilisons la fonction de cohérence pour sélectionner les nœuds enfants à descendre. Pour l'opérateur
>^ , cette fonction compare le point (2,7) avec le point central du nœud (4,4) et sélectionne les quadrants pouvant contenir les points recherchés, dans ce cas, les premier et quatrième quadrants.
Dans le nœud correspondant au premier quadrant, nous déterminons à nouveau les nœuds enfants à l'aide de la fonction de cohérence. Le point central est (6,6), et nous devons à nouveau regarder à travers les premier et quatrième quadrants.
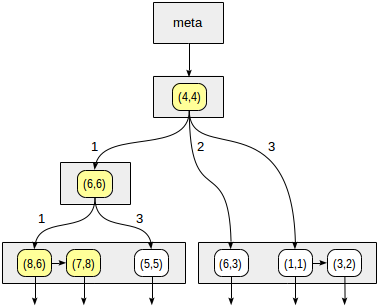
La liste des nœuds feuilles (8.6) et (7.8) correspond au premier quadrant, dont seul le point (7.8) remplit la condition de requête. La référence au quatrième quadrant est vide.
Dans le nœud interne (4.4), la référence au quatrième quadrant est également vide, ce qui termine la recherche.
postgres=# set enable_seqscan = off; postgres=# explain (costs off) select * from points where p >^ point '(2,7)';
QUERY PLAN ------------------------------------------------ Index Only Scan using points_quad_idx on points Index Cond: (p >^ '(2,7)'::point) (2 rows)
Internes
Nous pouvons explorer la structure interne des index SP-GiST en utilisant l'extension "
gevel ", qui a été mentionnée précédemment. La mauvaise nouvelle est qu'en raison d'un bogue, cette extension ne fonctionne pas correctement avec les versions modernes de PostgreSQL. La bonne nouvelle est que nous prévoyons d'étendre "pageinspect" avec la fonctionnalité de "gevel" (
discussion ). Et le bug a déjà été corrigé dans "pageinspect".
Encore une fois, la mauvaise nouvelle est que le patch est resté sans aucun progrès.
Par exemple, prenons la base de données de démonstration étendue, qui a été utilisée pour dessiner des images avec la carte du monde.
demo=# create index airports_coordinates_quad_idx on airports_ml using spgist(coordinates);
Tout d'abord, nous pouvons obtenir des statistiques pour l'indice:
demo=# select * from spgist_stats('airports_coordinates_quad_idx');
spgist_stats ---------------------------------- totalPages: 33 + deletedPages: 0 + innerPages: 3 + leafPages: 30 + emptyPages: 2 + usedSpace: 201.53 kbytes+ usedInnerSpace: 2.17 kbytes + usedLeafSpace: 199.36 kbytes+ freeSpace: 61.44 kbytes + fillRatio: 76.64% + leafTuples: 5993 + innerTuples: 37 + innerAllTheSame: 0 + leafPlaceholders: 725 + innerPlaceholders: 0 + leafRedirects: 0 + innerRedirects: 0 (1 row)
Et deuxièmement, nous pouvons sortir l'arbre d'index lui-même:
demo=# select tid, n, level, tid_ptr, prefix, leaf_value from spgist_print('airports_coordinates_quad_idx') as t( tid tid, allthesame bool, n int, level int, tid_ptr tid, prefix point,
tid | n | level | tid_ptr | prefix | leaf_value ---------+---+-------+---------+------------------+------------------ (1,1) | 0 | 1 | (5,3) | (-10.220,53.588) | (1,1) | 1 | 1 | (5,2) | (-10.220,53.588) | (1,1) | 2 | 1 | (5,1) | (-10.220,53.588) | (1,1) | 3 | 1 | (5,14) | (-10.220,53.588) | (3,68) | | 3 | | | (86.107,55.270) (3,70) | | 3 | | | (129.771,62.093) (3,85) | | 4 | | | (57.684,-20.430) (3,122) | | 4 | | | (107.438,51.808) (3,154) | | 3 | | | (-51.678,64.191) (5,1) | 0 | 2 | (24,27) | (-88.680,48.638) | (5,1) | 1 | 2 | (5,7) | (-88.680,48.638) | ...
Mais gardez à l'esprit que "spgist_print" ne produit pas toutes les valeurs de feuille, mais seulement la première de la liste, et montre donc la structure de l'index plutôt que son contenu complet.
Exemple: arbres k-dimensionnels
Pour les mêmes points dans le plan, nous pouvons également suggérer une autre façon de partitionner l'espace.
Dessinons
une ligne horizontale passant par le premier point indexé. Il divise l'avion en deux parties: supérieure et inférieure. Le deuxième point à indexer appartient à l'une de ces parties. À travers ce point, dessinons
une ligne verticale , qui divise cette partie en deux: droite et gauche. Nous dessinons à nouveau une ligne horizontale passant par le point suivant et une ligne verticale passant par le point suivant, et ainsi de suite.
Tous les nœuds internes de l'arborescence ainsi construits n'auront que deux nœuds enfants. Chacune des deux références peut conduire soit au nœud interne qui est le suivant dans la hiérarchie, soit à la liste des nœuds feuilles.
Cette méthode peut être facilement généralisée pour les espaces k-dimensionnels, et par conséquent, les arbres sont également appelés k-dimensionnels (arbres kD) dans la littérature.
Expliquer la méthode par l'exemple des aéroports:
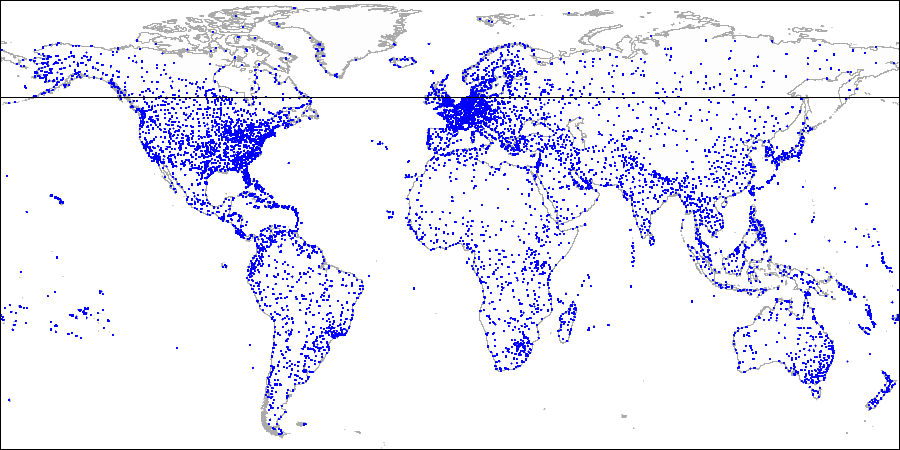Nous avons d'abord divisé l'avion en parties supérieure et inférieure ...
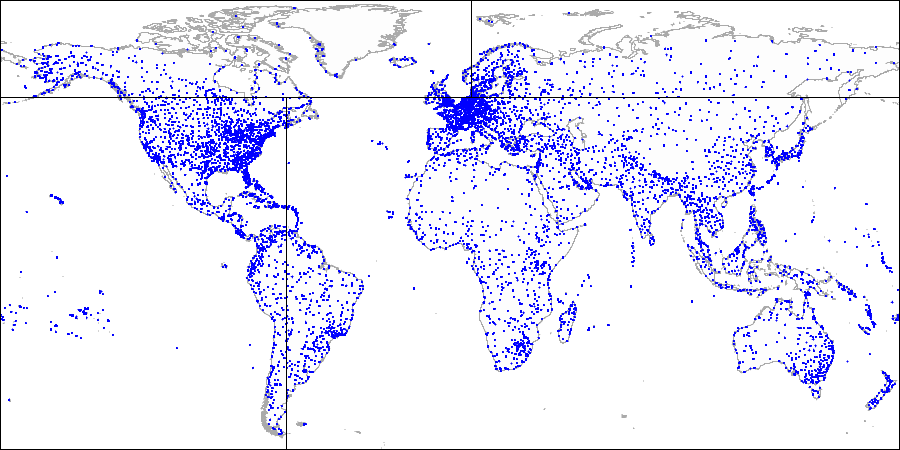Ensuite, nous avons divisé chaque partie en parties gauche et droite ...
Et ainsi de suite jusqu'à ce que nous obtenions le partitionnement final.Pour utiliser un partitionnement comme celui-ci, nous devons spécifier explicitement la classe d'opérateur
"kd_point_ops" lors de la création d'un index.
postgres=# create index points_kd_idx on points using spgist(p kd_point_ops);
Cette classe comprend exactement les mêmes opérateurs que la classe "par défaut" "quad_point_ops".
Internes
Lors de la recherche dans l'arborescence, nous devons tenir compte du fait que le préfixe dans ce cas n'est qu'une coordonnée plutôt qu'un point:
demo=# select tid, n, level, tid_ptr, prefix, leaf_value from spgist_print('airports_coordinates_kd_idx') as t( tid tid, allthesame bool, n int, level int, tid_ptr tid, prefix float,
tid | n | level | tid_ptr | prefix | leaf_value ---------+---+-------+---------+------------+------------------ (1,1) | 0 | 1 | (5,1) | 53.740 | (1,1) | 1 | 1 | (5,4) | 53.740 | (3,113) | | 6 | | | (-7.277,62.064) (3,114) | | 6 | | | (-85.033,73.006) (5,1) | 0 | 2 | (5,12) | -65.449 | (5,1) | 1 | 2 | (5,2) | -65.449 | (5,2) | 0 | 3 | (5,6) | 35.624 | (5,2) | 1 | 3 | (5,3) | 35.624 | ...
Exemple: arbre radix
Nous pouvons également utiliser SP-GiST pour implémenter un arbre radix pour les chaînes. L'idée d'un arbre Radix est qu'une chaîne à indexer n'est pas entièrement stockée dans un nœud feuille, mais est obtenue en concaténant les valeurs stockées dans les nœuds au-dessus de celui-ci jusqu'à la racine.
Supposons que nous devons indexer les URL des sites: "postgrespro.ru", "postgrespro.com", "postgresql.org" et "planet.postgresql.org".
postgres=# create table sites(url text); postgres=# insert into sites values ('postgrespro.ru'),('postgrespro.com'),('postgresql.org'),('planet.postgresql.org'); postgres=# create index on sites using spgist(url);
L'arbre se présente comme suit:
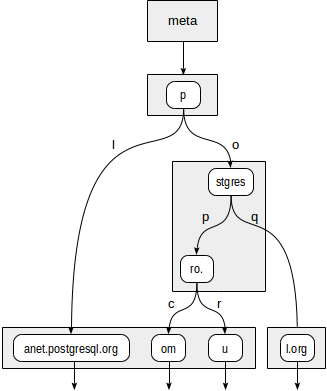
Les nœuds internes des préfixes de stockage d'arborescence communs à tous les nœuds enfants. Par exemple, dans les nœuds enfants de "stgres", les valeurs commencent par "p" + "o" + "stgres".
Contrairement à Quadtrees, chaque pointeur vers un nœud enfant est en outre étiqueté avec un caractère (plus exactement, avec deux octets, mais ce n'est pas si important).
La classe d'opérateur "Text_ops" prend en charge les opérateurs de type arbre B: "égal", "supérieur" et "inférieur":
postgres=# select amop.amopopr::regoperator, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'text_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'spgist' and amop.amoplefttype = opc.opcintype;
amopopr | amopstrategy -----------------+-------------- ~<~(text,text) | 1 ~<=~(text,text) | 2 =(text,text) | 3 ~>=~(text,text) | 4 ~>~(text,text) | 5 <(text,text) | 11 <=(text,text) | 12 >=(text,text) | 14 >(text,text) | 15 (9 rows)
La distinction des opérateurs avec des tildes est qu'ils manipulent des
octets plutôt que des
caractères .
Parfois, une représentation sous la forme d'un arbre radix peut s'avérer beaucoup plus compacte que l'arbre B car les valeurs ne sont pas entièrement stockées, mais reconstruites au fur et à mesure des besoins en descendant dans l'arbre.
Considérez une requête:
select * from sites where url like 'postgresp%ru' . Elle peut être réalisée à l'aide de l'index:
postgres=# explain (costs off) select * from sites where url like 'postgresp%ru';
QUERY PLAN ------------------------------------------------------------------------------ Index Only Scan using sites_url_idx on sites Index Cond: ((url ~>=~ 'postgresp'::text) AND (url ~<~ 'postgresq'::text)) Filter: (url ~~ 'postgresp%ru'::text) (3 rows)
En fait, l'index est utilisé pour rechercher des valeurs supérieures ou égales à "postgresp", mais inférieures à "postgresq" (Index Cond), puis les valeurs correspondantes sont choisies dans le résultat (Filter).
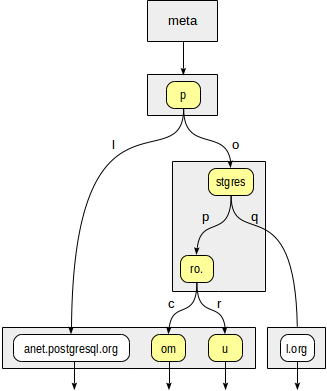
Premièrement, la fonction de cohérence doit décider vers quels nœuds enfants de la racine "p" nous devons descendre. Deux options sont disponibles: "p" + "l" (pas besoin de descendre, ce qui est clair même sans plonger plus profondément) et "p" + "o" + "stgres" (continuer la descente).
Pour le nœud "stgres", un appel à la fonction de cohérence est à nouveau nécessaire pour vérifier "postgres" + "p" + "ro". (continuer la descente) et "postgres" + "q" (pas besoin de descendre).
Pour "ro". nœud et tous ses nœuds feuilles enfants, la fonction de cohérence répondra "oui", donc la méthode d'index retournera deux valeurs: "postgrespro.com" et "postgrespro.ru". Une valeur correspondante en sera sélectionnée au stade du filtrage.
Internes
Lors de la recherche dans l'arborescence, nous devons prendre en compte les types de données:
postgres=# select * from spgist_print('sites_url_idx') as t( tid tid, allthesame bool, n int, level int, tid_ptr tid, prefix text,
Propriétés
Examinons les propriétés de la méthode d'accès SP-GiST (des requêtes
ont été fournies précédemment ):
amname | name | pg_indexam_has_property --------+---------------+------------------------- spgist | can_order | f spgist | can_unique | f spgist | can_multi_col | f spgist | can_exclude | t
Les index SP-GiST ne peuvent pas être utilisés pour le tri et pour la prise en charge de la contrainte unique. De plus, des index comme celui-ci ne peuvent pas être créés sur plusieurs colonnes (contrairement à GiST). Mais il est autorisé d'utiliser de tels index pour prendre en charge les contraintes d'exclusion.
Les propriétés de couche d'index suivantes sont disponibles:
name | pg_index_has_property ---------------+----------------------- clusterable | f index_scan | t bitmap_scan | t backward_scan | f
La différence avec GiST ici est que le clustering est impossible.
Et finalement, les propriétés de couche de colonne sont les suivantes:
name | pg_index_column_has_property --------------------+------------------------------ asc | f desc | f nulls_first | f nulls_last | f orderable | f distance_orderable | f returnable | t search_array | f search_nulls | t
Le tri n'est pas pris en charge, ce qui est prévisible. Les opérateurs de distance pour la recherche des voisins les plus proches ne sont pas disponibles pour l'instant dans SP-GiST. Très probablement, cette fonctionnalité sera prise en charge à l'avenir.
Il est pris en charge dans le prochain PostgreSQL 12, le correctif de Nikita Glukhov.
SP-GiST peut être utilisé pour l'analyse d'index uniquement, au moins pour les classes d'opérateurs décrites. Comme nous l'avons vu, dans certains cas, les valeurs indexées sont explicitement stockées dans les nœuds feuilles, tandis que dans les autres, les valeurs sont reconstruites partie par partie pendant la descente de l'arbre.
Nulls
Pour ne pas compliquer l'image, nous n'avons pas mentionné de NULL jusqu'à présent. Il ressort clairement des propriétés d'index que les valeurs NULL sont prises en charge. Vraiment:
postgres=# explain (costs off) select * from sites where url is null;
QUERY PLAN ---------------------------------------------- Index Only Scan using sites_url_idx on sites Index Cond: (url IS NULL) (2 rows)
Cependant, NULL est quelque chose d'étranger pour SP-GiST. Tous les opérateurs de la classe d'opérateur "spgist" doivent être stricts: un opérateur doit retourner NULL chaque fois que l'un de ses paramètres est NULL. La méthode elle-même garantit ceci: les valeurs NULL ne sont tout simplement pas transmises aux opérateurs.
Mais pour utiliser la méthode d'accès pour l'analyse d'index uniquement, les valeurs NULL doivent de toute façon être stockées dans l'index. Et ils sont stockés, mais dans un arbre séparé avec sa propre racine.
Autres types de données
En plus des arbres de points et de radix pour les chaînes, d'autres méthodes basées sur SP-GiST sont également implémentées PostgreSQL:
- La classe d'opérateur Box_ops fournit un quadtree pour les rectangles.
Chaque rectangle est représenté par un point dans un espace à quatre dimensions , donc le nombre de quadrants est égal à 16. Un indice comme celui-ci peut battre GiST en performance quand il y a beaucoup d'intersections des rectangles: dans GiST, il est impossible de tracer des frontières afin de séparer les objets qui se croisent les uns des autres, alors qu'il n'y a pas de tels problèmes avec les points (même en quatre dimensions).
- La classe d'opérateur "Range_ops" fournit un quadtree pour les intervalles.
Un intervalle est représenté par un point à deux dimensions : la limite inférieure devient l'abscisse et la limite supérieure devient l'ordonnée.
Continuez à lire .