👥 👨🏽‍💼 👩‍👩‍👧‍👧 Nous modélisons l'algorithme MUSIC pour déterminer la direction d'arrivée d'une onde électromagnétique 👧 🎋 👌🏼

aaspcats

Préface

Je vais commencer mon introduction de loin. Il était une fois, dans le lointain 2016-2017, votre humble serviteur a réussi à suivre une formation de six mois dans la ville éloignée d' Ilmenau (Allemagne), où il a réussi (dans l'ensemble) le programme de maîtrise Communications et traitement du signal . Le programme n’a pas été facile, mais maintenant il est même agréable de le rappeler. Parfois ...

Donc, à la fin de cette formation, en plus du diplôme, j'ai encore pas mal de matériel différent entre les mains, que je pensais mal de ne pas partager.

Un de ces matériaux est devant vous.

Quels objectifs ai-je poursuivis lors de la préparation du séminaire :

parler de certaines approches «intelligentes» déjà établies dans le domaine des réseaux d'antennes les plus accessibles et le faire en russe;
effectuer une petite simulation en Python 3 afin d'inciter les collègues ingénieurs radio à regarder de plus près les langages de programmation (si vous ne l'avez pas déjà regardé de près);
fournir des liens vers une bonne littérature de langue anglaise - sans lire des sources étrangères, maintenant, hélas, nulle part.

À considérer :

La méthode MUSIC (MUltiple SIgnal Classification) - celle-ci, en fait, se réfère à l'aperçu.

Un exemple de formation de graphiques et de la méthode MVDR peut être trouvé ici (s'il y a des questions ou des suggestions de matériel supplémentaire, la discussion peut être poursuivie sur Github.Gist).

Comme je l'ai dit plus haut, nous utiliserons Python, à savoir:

import numpy as np import matplotlib.pyplot as plt

Pourquoi pas MATLAB, l'un des candidats les plus populaires et les plus pratiques pour la modélisation d'algèbre linéaire, demandez-vous? Parce que, je veux montrer qu'un travail similaire peut être effectué en Python, et la portée de Python est beaucoup plus large que celle de MATLAB. Par conséquent, être familier avec la syntaxe Python est une chose utile, à mon avis.

Commençons!

Les formules sont préparées via https://upmath.me/ . Merci aux créateurs pour un excellent outil!

Énoncé du problème

Supposons qu'il existe un réseau d'antennes linéaire composé d'un certain nombre d'éléments espacés les uns des autres $\ Delta = \ frac {\ lambda} {2}$ (étape du réseau d'antennes), où $\ lambda$ - la longueur de l'onde électromagnétique porteuse (EM).

Des ondes électromagnétiques tombent sur ce réseau d'antennes de différentes directions.

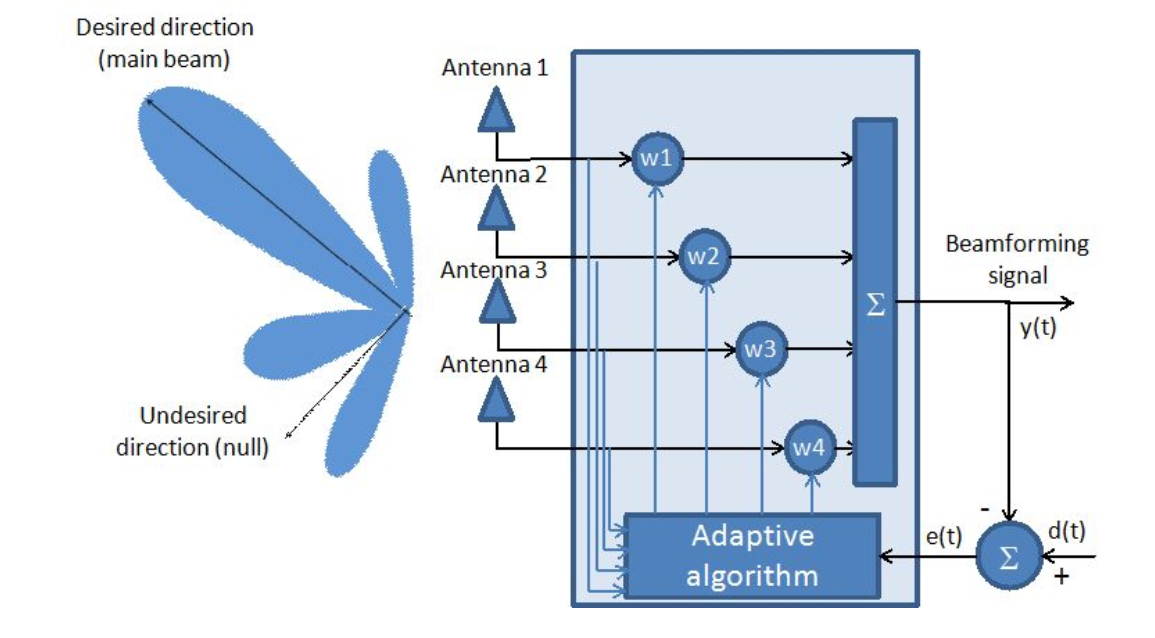
Fig. 1. Système d'antenne adaptatif.

Comme le montre la figure, le réseau d'antennes est considéré comme un filtre adaptatif.

En fait, trouver le vecteur optimal de coefficients ( $\ mathbf {w} _ {opt}$ ) est la tâche principale des réseaux d'antennes adaptatifs d'un point de vue mathématique.

Au départ, nous ne savons pas de quelles directions particulières proviennent les signaux et combien d'entre eux. C'est pour résoudre cette contradiction que nous utiliserons l'algorithme MUSIC, un algorithme d'estimation des fréquences spatiales à haute résolution.

Simulation de signal reçu

Nous pouvons présenter le modèle du signal reçu à travers la formule:

$\ mathbf {X} = \ mathbf {A} \ mathbf {S} + \ mathbf {N}$

où $\ mathbf {A} = [\ mathbf {a} (\ theta_1) \ quad \ mathbf {a} (\ theta_2) \ quad ... \ quad \ mathbf {a} (\ theta_d)]$ - matrice de vecteurs de balayage (vecteurs de direction) du réseau d'antennes ( $a_i = \ exp (-j \ mu m_i)$ , $m = 0, 1 ... (M-1)$ , $M$ - le nombre d'éléments du réseau d'antennes, $d$ - le nombre de sources d'ondes électromagnétiques, $\ thêta$ - l'angle de la direction d'arrivée de l'onde EM), $\ mathbf {S}$ - matrice de caractères transmis, et $\ mathbf {N}$ - matrice de bruit additif.

Fig. 2. Réseau d'antennes linéaires omnidirectionnelles (ULAA - réseau d'antennes linéaires uniformes) [1, p. 32].

Repensons cette formule de façon «quotidienne»: sur notre grille, nous obtenons un certain «désordre» de divers signaux, que nous désignons par $\ mathbf {X}$ . Nous ne recevons pas explicitement d'informations sur le nombre de sources et de directions, cependant, des informations à ce sujet sont néanmoins contenues dans le signal reçu.

Nous commençons à chercher!

Pour ce faire, ils procèdent généralement à des manipulations non pas avec les matrices d'amplitudes de signaux complexes elles-mêmes, mais avec leurs covariances (c'est-à-dire, essentiellement, avec des puissances):

$\ mathbf {R} _ {xx} = \ mathbf {X} \ mathbf {X} ^ H = \ mathbf {A} \ mathbf {R} _ {ss} \ mathbf {A} ^ H + \ mathbf {R} _ {nn}$

Les conditions

Nous introduisons une condition importante à considérer: la limite de résolution d'angle de Rayleigh:

$sin (\ theta_R) = \ frac {\ lambda} {D}$

où $D = M \ Delta$ Est la longueur du réseau linéaire.

Nous redéfinissons l'angle d'arrivée d'une onde électromagnétique à travers le concept de fréquence spatiale:

$\ mu_R = \ frac {2 \ pi} {\ lambda} \ Delta sin (\ theta_R) = \ frac {2 \ pi} {\ lambda} \ Delta \ frac {\ lambda} {\ Delta M} = \ frac { 2 \ pi} {M}$

où $\ mu_R$ - il existe une largeur standard du lobe principal du faisceau ( largeur de faisceau standard ).

Pour vérifier l'efficacité de notre méthode et dans quelles conditions, nous introduisons quelques valeurs données pour la séparation angulaire:

$\ mu_1 = - \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = \ mu_R \ quad$ - division en une largeur de faisceau;
$\ mu_1 = -0,5 \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = 0,5 \ mu_R \ quad$ - division en une seconde largeur de faisceau;
$\ mu_1 = -0.3 \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = 0.3 \ mu_R \ quad$ - division en trois dixièmes de la largeur du faisceau.

Définissez les paramètres d'entrée:

 M = 10 #    () SNR = 10 #  - (dB) d = 3 #     N = 50 #  "" (snapshots) S = ( np.sign(np.random.randn(d,N)) + 1j * np.sign(np.random.randn(d,N)) ) / np.sqrt(2) # QPSK W = ( np.random.randn(M,N) + 1j * np.random.randn(M,N) ) / np.sqrt(2) * 10**(-SNR/20) # AWGN #  : # sqrt(N0/2)*(G1 + jG2), #  G1  G2 -   . # .. Es( )  QPSK  1 ,    (noise spectral density): # N0 = (Es/N)^(-1) = SNR^(-1) [] (   ,  SNR = Es/N0); #    : # SNR_dB = 10log10(SNR) => N0_dB = -10log10(SNR) = -SNR_dB []; #    SNR    (..  ),   : # SNR = 10^(SNR_dB/10) => sqrt(N0) = (10^(-SNR_dB/10))^(1/2) = 10^(-SNR_dB/20) mu_R = 2*np.pi / M

Un peu de théorie sur la méthode elle-même

Tout d'abord, nous notons que l'ancêtre de la méthode MUSIC est la méthode Pisarenko (1973). Le problème considéré de la méthode de Pisarenko était d'estimer les fréquences de la somme des exponentielles complexes dans le bruit blanc. V.F. Pisarenko a démontré que des fréquences peuvent être trouvées à partir de vecteurs propres correspondant à la valeur propre minimale de la matrice d'autocorrélation. Par la suite, cette méthode est devenue un cas particulier de la méthode MUSIC. [2, p. 459]

Schmidt et ses collègues ont proposé l'algorithme de classification de signaux multiples (MUSIC) en 1979 [4]. L'approche principale de cet algorithme est de décomposer la matrice de covariance du signal reçu en valeurs propres. Puisque cet algorithme prend en compte le bruit non corrélé, la matrice de covariance générée a une forme diagonale. Ici, les sous-espaces de signal et de bruit sont calculés à l'aide d'une algèbre linéaire et sont orthogonaux entre eux. Par conséquent, l'algorithme utilise la propriété d'orthogonalité pour extraire les sous-espaces de signal et de bruit [5].

L'algorithme MUSIC généralisé peut être défini comme suit:

Trouver la matrice de covariance $\ mathbf {R} _ {xx}$
Trouvez des vecteurs propres via EVD ou un autre algorithme numérique approprié:

$\ mathbf {R} _ {xx} = \ mathbf {U} \ mathbf {\ Lambda} \ mathbf {U} ^ H \ qquad (1)$

Trouvez le pseudo-spectre (pourquoi avec le pseudo préfixe, nous discuterons ci-dessous) MUSIQUE à travers la formule suivante:

$P_ {MU} (e ^ {j \ omega}) = \ frac {1} {\ sum \ limits_ {i = d + 1} ^ {M} | \ mathbf {a} ^ H \ mathbf {u} _i | ^ 2} \ qquad (2)$

où $\ mathbf {a} = \ begin {bmatrix} e ^ {j0 \ omega} & e ^ {j1 \ omega} & e ^ {j2 \ omega} & ... & e ^ {j (M-1) \ omega } \ end {bmatrix} ^ T$ Est le vecteur des exponentielles pour la fréquence ω se situant dans une plage donnée, et $\ mathbf {u} _i$ - le i-ème vecteur propre de la matrice de covariance (1) correspondant au sous-espace de bruit de la matrice (1) - d'où l'indexation avec $d + 1$ ( $d$ Est le rang de la matrice (1)).

Pour plus de clarté, essayez d'exécuter le script MATLAB approprié fourni par référence . Faites attention à deux points principaux:
au lieu de calculer le carré de la deuxième norme du dénominateur (2), les auteurs appliquent l'algorithme FFT aux vecteurs propres, ce qui facilite la modélisation en utilisant des fonctions intégrées et, en général, ne contredit pas la théorie d'un point de vue mathématique;
la matrice de covariance est calculée à l'aide de matrices convolutionnelles; une approche différente a été montrée ci-dessus pour estimer les fréquences spatiales.

Comme vous pouvez le deviner d'après le nom, MUSIC est également une méthode classique pour estimer la direction de réception à haute résolution. L'algorithme de calcul des pseudo-spectres dans ce contexte est donné ci-dessous:

on retrouve la matrice de covariance du signal reçu;
trouver le sous-espace zéro $\ mathbf {U} _0$ :

$\ mathbf {U} = [\ mathbf {U} _s \ quad \ mathbf {U} _0]$

sélectionnez une plage de recherche:

$a (\ mu) = \ begin {bmatrix} e ^ {j0 \ mu_1} & ... & e ^ {j0 \ mu_Q} \\ ... & ... & ... \\ e ^ {j ( M-1) \ mu_1} & ... & e ^ {j (M-1) \ mu_Q} \ end {bmatrix}$

où $\ mu = - \ frac {2 \ pi f_c} {c} \ Delta sin \ theta = - \ frac {2 \ pi} {\ lambda} \ Delta sin \ theta$

calculer le pseudo-spectre:

$P_ {MU} (\ theta) = \ frac {\ mathbf {a} ^ H (\ theta) \ mathbf {a} (\ theta)} {\ mathbf {a} ^ H (\ theta) \ mathbf {U} _0 \ mathbf {U} _0 ^ H \ mathbf {a} (\ theta)}$

La relation entre l'analyse spectrale et l'analyse des angles d'arrivée (DoA - direction de l'arriaval) des ondes EM est décrite dans le tableau 1.

Tableau 1 Communication entre les applications MUSIC : traitement du réseau de signaux et recherche harmonique [6].

Variable	Traitement de la matrice de signaux	Recherche harmonique
$M$	Nombre de capteurs	Le nombre de périodes
$N$	Le nombre de périodes	Nombre d'expériences
$d$	Nombre de fronts d'onde	Le nombre de composants complexes
$\ mu$	Fréquences spatiales	Fréquences normalisées

En général, le processus de réception à travers des tableaux (réseaux) peut être comparé au processus de discrétisation classique, car en fait, chaque capteur, recevant une onde avec un certain retard de phase (c'est-à-dire avec un certain retard), remplit les fonctions d'une impulsion delta d'échantillonnage. Le nombre de réalisations (expériences) de l'analyse spectrale classique correspondra au nombre de segments temporels (instantanés). Chaque source aura son propre front d'onde, ce qui équivaut au nombre de sinusoïdes uniques du signal dans le cas de l'analyse spectrale.

Et maintenant revenons au moment du calcul des vecteurs propres. Nous avons déjà mentionné ci-dessus que les vecteurs $a (\ theta_i) \ epsilon A$ où $i = 1,2, .., d$ sont orthogonales au sous-espace de bruit de la matrice de covariance, à savoir:

$a (\ theta_i) ^ TU_0 = 0 ^ T$

En fait, nous voyons un système d'équations, résoudre dont nous pouvons trouver les racines - vecteurs propres. Une telle méthode, contrairement aux algorithmes numériques (qui, comme nous l'avons noté ci-dessus, s'applique à EVD), permet d'obtenir des valeurs propres réelles plutôt qu'approximatives. C'est pourquoi cette approche nous permet d'obtenir non pas un pseudospectre, mais un spectre. La même idée a formé la base de l'algorithme Root MUSIC .

Modélisation

Pouf! Enfin, toutes les formules sont décrites et quelque peu expliquées. Nous pouvons commencer la modélisation.

 cases = [[-1., 0, 1.], [-0.5, 0, 0.5], [-0.3, 0, 0.3],] for idxm, c in enumerate(cases): #   ( ): mu_1 = c[0]*mu_R mu_2 = c[1]*mu_R mu_3 = c[2]*mu_R #   a_1 = np.exp(1j*mu_1*np.arange(M)) a_2 = np.exp(1j*mu_2*np.arange(M)) a_3 = np.exp(1j*mu_3*np.arange(M)) A = (np.array([a_1, a_2, a_3])).T #    X = np.dot(A,S) + W #    R = np.dot(X,np.matrix(X).H) U, Sigma, Vh = np.linalg.svd(X, full_matrices=True) U_0 = U[:,d:] #   thetas = np.arange(-90,91)*(np.pi/180) #   mus = np.pi*np.sin(thetas) #    a = np.empty((M, len(thetas)), dtype = complex) for idx, mu in enumerate(mus): a[:,idx] = np.exp(1j*mu*np.arange(M)) # MVDR: S_MVDR = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MVDR[idx] = 1 / (np.dot(np.matrix(a_idx).H, np.dot(np.linalg.pinv(R),a_idx))) # MUSIC: S_MUSIC = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MUSIC[idx] = np.dot(np.matrix(a_idx).H,a_idx)\ / (np.dot(np.matrix(a_idx).H, np.dot(U_0,np.dot(np.matrix(U_0).H,a_idx)))) plt.subplots(figsize=(10, 5), dpi=150) plt.semilogy(thetas*(180/np.pi), np.real( (S_MVDR / max(S_MVDR))), color='green', label='MVDR') plt.semilogy(thetas*(180/np.pi), np.real((S_MUSIC/ max(S_MUSIC))), color='red', label='MUSIC') plt.grid(color='r', linestyle='-', linewidth=0.2) plt.xlabel('Azimuth angles θ (degrees)') plt.ylabel('Power (pseudo)spectrum (normalized)') plt.legend() plt.title('Case #'+str(idxm+1)) plt.show()

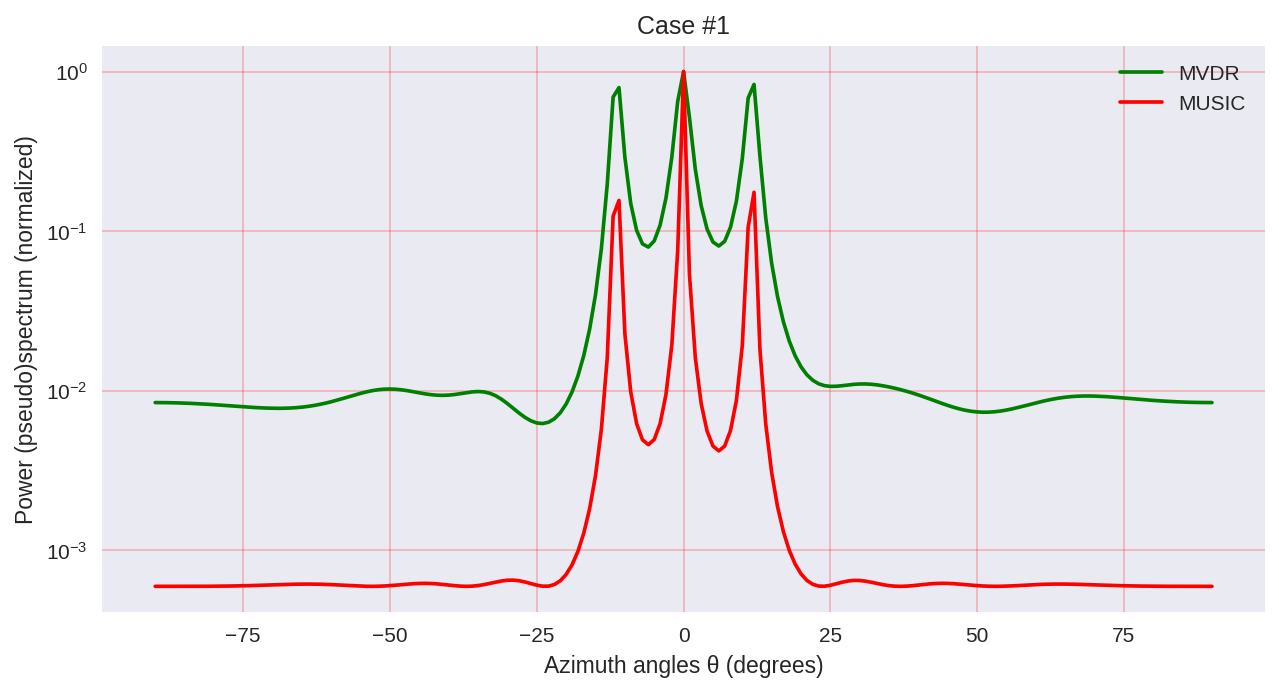
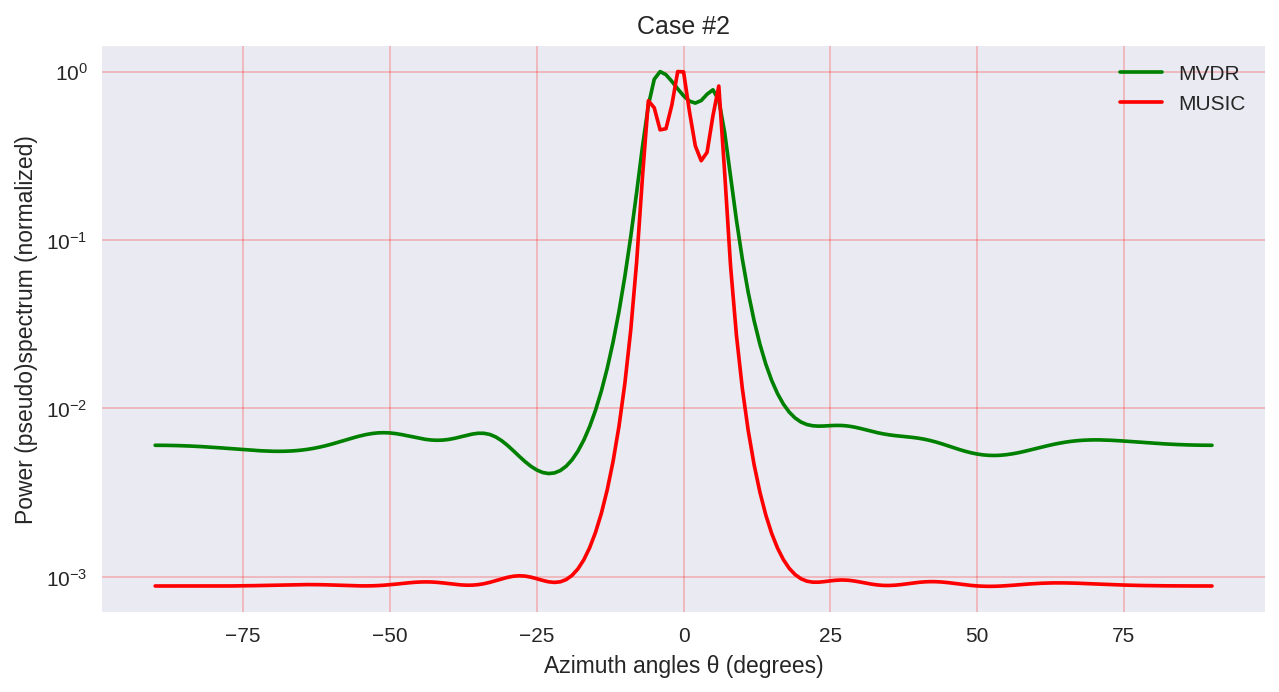
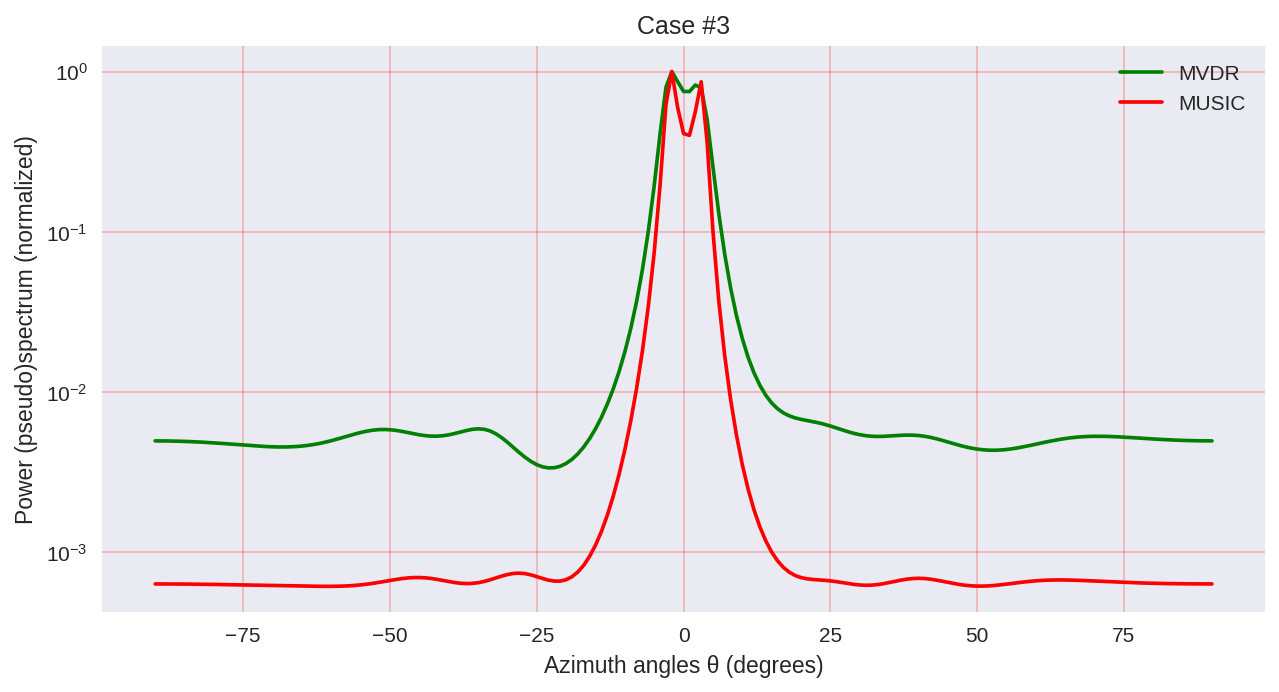
Comme nous pouvons le voir, MUSIC a une résolution plus élevée et permet d'obtenir, en général, de meilleurs résultats que, par exemple, le MVDR permet - le même représentant des méthodes paramétriques d'analyse spectrale.

Cependant, gardez à l'esprit que lorsque vous utilisez MUSIC, nous utilisons des algorithmes plus coûteux en calcul, tels que EVD ou SVD, qui sont à un certain prix pour une plus grande précision.

De telles choses.

Liste de la littérature utilisée:

Haykin, Simon et KJ Ray Liu. Manuel sur le traitement des réseaux et les réseaux de capteurs. Vol. 63. John Wiley & Sons, 2010. pp. 102-107
Hayes MH Traitement et modélisation numérique du signal statistique. - John Wiley & Sons, 2009.
Haykin, Simon S. Théorie du filtre adaptatif. Pearson Education India, 2008. pp. 422-427
Richmond, Christ D. «Algorithme de Capon, prédiction SNR du seuil d'erreur quadratique moyenne et probabilité de résolution». Transactions IEEE sur le traitement du signal 53.8 (2005): 2748-2764.
SKP Gupta, MUSIC et algorithme MUSIC amélioré pour estimer la dorection de l'arrivée, IEEE, 2015.
Conférences du professeur Martin Haardt ( array array )

Nous modélisons l'algorithme MUSIC pour déterminer la direction d'arrivée d'une onde électromagnétique