Deep Learning en calcul de flux optique

Avec l'avènement de nombreuses architectures de réseaux de neurones différentes, de nombreuses techniques classiques de vision par ordinateur appartiennent au passé. De moins en moins, les gens utilisent SIFT et HOG pour la détection d'objets et MBH pour la reconnaissance des actions, et s'ils l'utilisent, cela ressemble plus à des panneaux fabriqués à la main pour les grilles correspondantes. Aujourd'hui, nous allons examiner l'un des problèmes classiques de CV dans lesquels les méthodes classiques tiennent toujours la tête, tandis que les architectures DL les respirent langoureusement à l'arrière de la tête.

Estimation du flux optique

La tâche de calculer le flux optique entre deux images (généralement entre des images adjacentes d'une vidéo) est de construire un champ vectoriel $$$O$la même taille, d'ailleurs $$$O (i, j)$correspondra au vecteur de déplacement apparent des pixels $$$(i, j)$de la première image à la seconde. En construisant un tel champ vectoriel entre toutes les images adjacentes de la vidéo, nous obtenons une image complète de la façon dont certains objets s'y sont déplacés. En d'autres termes, c'est la tâche de suivre tous les pixels d'une vidéo. Le flux optique est extrêmement utilisé - dans les tâches de reconnaissance d'action, par exemple, un tel champ vectoriel vous permet de vous concentrer sur les mouvements se produisant sur la vidéo et de vous éloigner de son contexte [7]. Les applications encore plus courantes sont l'odométrie visuelle, la compression vidéo, le post-traitement (par exemple, l'ajout d'un effet de ralenti) et bien plus encore.



Il y a de la place pour certaines ambiguïtés - qu'est-ce qui est considéré exactement comme un biais visible du point de vue des mathématiques? Habituellement, on suppose que les valeurs des pixels passent d'une image à l'autre sans changement, en d'autres termes:

$$

$$I (i, j, t) = I (i + u_i, j + u_j, t + 1),$$

où $$$I (i, j, t)$- intensité des pixels en coordonnées $$$(i, j)$puis flux optique $$$(u_i, u_j)$montre où ce pixel s'est déplacé au point suivant dans le temps (c'est-à-dire sur la prochaine image).

Dans l'image, cela ressemble à ceci:





Visualiser un champ vectoriel directement avec des vecteurs est visuel, mais pas toujours pratique, donc la deuxième façon courante est de visualiser avec des couleurs:





Chaque couleur de cette image code pour un vecteur spécifique. Pour plus de simplicité, les vecteurs de plus de 20 sont rognés et le vecteur lui-même peut être restauré par couleur à partir de l'image suivante:




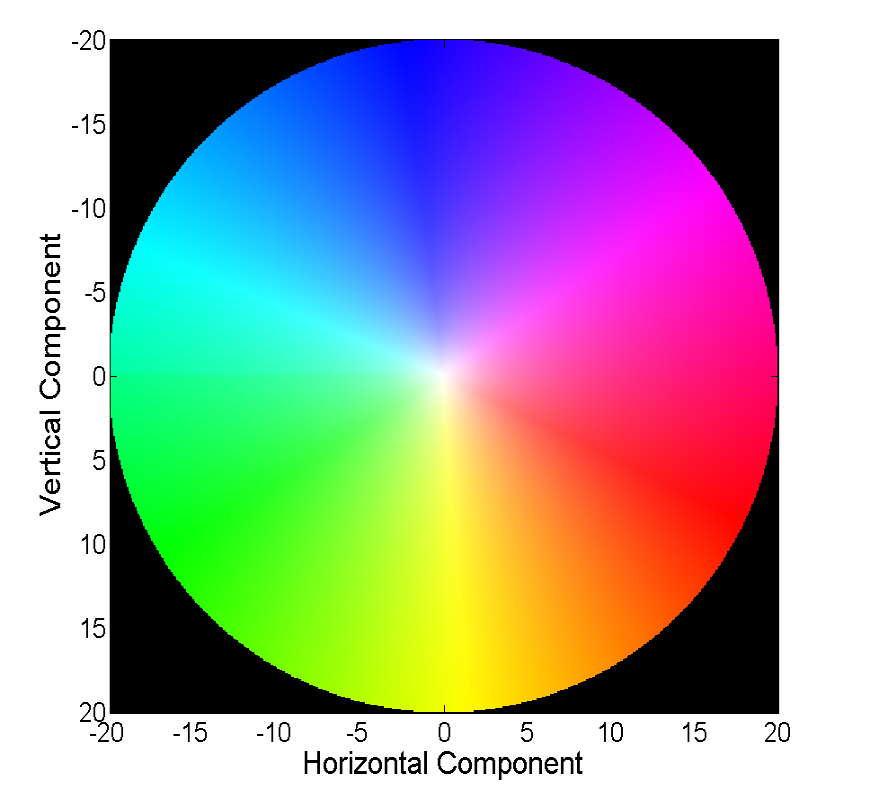
Les méthodes classiques ont atteint une assez bonne précision, ce qui a parfois un prix. Nous considérerons les progrès réalisés par les réseaux de neurones dans la résolution de ce problème au cours des 4 dernières années.

Données et métriques

Deux mots sur quels jeux de données étaient disponibles et populaires au début de notre histoire (c'est-à-dire 2015), et aussi comment ils mesurent la qualité de l'algorithme résultant.

Middlebury

Un petit ensemble de données de 8 paires d'images avec de petits décalages, qui, néanmoins, est parfois utilisé dans la validation d'algorithmes pour calculer le flux optique même maintenant.

Kitty

Il s'agit d'un ensemble de données balisé pour des applications pour les voitures autonomes et assemblé à l'aide de la technologie LIDAR. Il est largement utilisé pour valider les algorithmes de calcul de flux optique et contient de nombreux cas assez compliqués avec des transitions nettes entre les trames.

Sintel

Une autre référence très commune, créée sur la base de la bande dessinée ouverte et dessinée dans Blender Sintel en deux versions, qui sont désignées comme propres et finales. La seconde est beaucoup plus compliquée, car contient beaucoup d'effets atmosphériques, de bruit, de flou et d'autres problèmes pour les algorithmes de calcul du flux optique.

EPE

La fonction d'erreur standard pour la tâche de calcul du flux optique est End Point Error ou EPE. Il s'agit simplement de la distance euclidienne entre l'algorithme calculé et le véritable flux optique, moyenne sur tous les pixels.

Flownet (2015)

En se lançant dans la construction d'une architecture de réseau neuronal pour la tâche de calcul du flux optique en 2015, les auteurs (des universités de Munich et de Fribourg) ont rencontré deux problèmes: il n'y avait pas un grand ensemble de données marqué pour cette tâche, et le marquer manuellement serait difficile (essayez de marquer où je me suis déplacé) chaque pixel de l'image sur l'image suivante), tout d'abord. Cette tâche était très différente de toutes les tâches qui ont été résolues avec l'aide des architectures CNN avant cela, deuxièmement. En fait, il s'agit d'une tâche de régression pixel par pixel, ce qui la rend similaire à la tâche de segmentation (classification pixel par pixel), mais au lieu d'une image, nous avons deux entrées, et intuitivement, les signes doivent en quelque sorte montrer la différence entre les deux images. Comme première itération, il a été décidé de simplement insérer deux images RVB en entrée (après avoir reçu, en fait, une image à 6 canaux), entre lesquelles nous voulons calculer le flux optique, et de prendre U-net comme une architecture avec un certain nombre de changements. Ce réseau s'appelait FlowNetS (S signifie Simple):





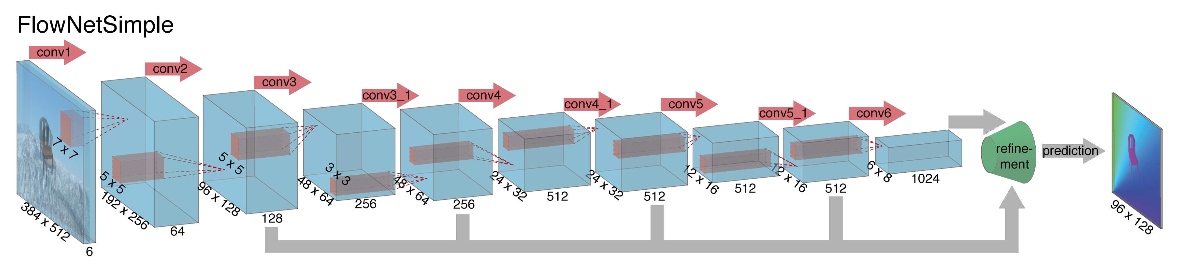
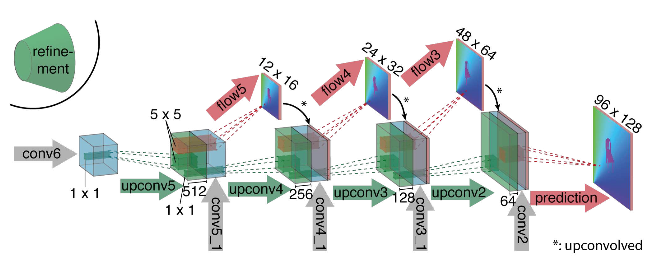
Comme on peut le voir sur le schéma, l'encodeur n'est pas perceptible en aucune façon, le décodeur diffère des options classiques à plusieurs égards:

1. La prédiction du flux optique se fait non seulement à partir du dernier niveau, mais aussi à partir de tous les autres. Pour obtenir la vérité au sol pour le i-ème niveau du décodeur, la cible d'origine (c'est-à-dire le flux optique) est simplement réduite (presque la même que l'image) à la résolution souhaitée, et le prédicat obtenu au i-ème niveau va plus loin, t c'est-à-dire qu'il est concaténé avec une carte des caractéristiques émergeant de ce niveau. La fonction générale des pertes d'entraînement sera une somme pondérée des pertes de tous les niveaux du décodeur, tandis que le poids lui-même sera d'autant plus important que le niveau sera proche de la sortie du réseau. Les auteurs ne donnent pas d'explication pourquoi cela est fait, mais la raison la plus probable est le fait que les mouvements nets sont mieux détectés à des niveaux précoces, alors les vecteurs ne seront pas si grands sur le flux optique de résolution inférieure.
2. Le diagramme montre que la résolution d'entrée des images est 384x512 et la résolution de sortie est quatre fois inférieure. Les auteurs ont remarqué que si vous augmentez cette sortie à 384x512 par simple interpolation bilinéaire, cela donnera la même qualité que si vous associez deux niveaux supplémentaires du décodeur. Vous pouvez également utiliser l'approche variationnelle [2], qui prouve la qualité (+ v dans le tableau avec la qualité).
3. Comme dans U-net, les cartes attributaires de l'encodeur sont envoyées au décodeur et concaténées comme indiqué dans le diagramme.

Pour comprendre comment les auteurs ont essayé d'améliorer leur ligne de base, vous devez savoir quelle est la corrélation entre les images et pourquoi elle peut être utile dans le calcul du flux optique. Donc, ayant deux images et sachant que la seconde est la prochaine image de la vidéo par rapport à la première, nous pouvons essayer de comparer la zone autour du point de la première image (pour laquelle nous voulons trouver un décalage vers la deuxième image) avec des zones de même taille dans la deuxième image. De plus, en supposant que le décalage ne puisse pas être trop important par unité de temps, la comparaison ne peut être envisagée que dans un certain voisinage du point de départ. Pour cela, une corrélation croisée est utilisée. Illustrons par un exemple.

Prenez deux images adjacentes de la vidéo, nous voulons déterminer où un certain point est passé de la première image à la seconde. Supposons qu'une zone autour de ce point ait changé de la même manière. En effet, les pixels voisins d'une vidéo sont généralement décalés ensemble, comme très probablement, visuellement, font partie d'un objet. Cette hypothèse est activement utilisée, par exemple, dans les approches différentielles, qui peuvent être lues plus en détail dans [5], [6].

fig, ax = plt.subplots(1, 2, figsize=(20, 10)) ax[0].imshow(frame1) ax[1].imshow(frame2); 

Essayons de prendre un point au centre de la patte du chaton et de le trouver sur la deuxième image. Prenez un espace autour d'elle.

 patch1 = frame1[90:190, 140:250] plt.imshow(patch1); 

Nous calculons la corrélation entre cette zone (dans la littérature anglaise, écrivez souvent un modèle ou un patch à partir de la première image) et la deuxième image. Le modèle «parcourra» simplement la deuxième image et calculera la valeur suivante entre lui-même et des morceaux de même taille dans la deuxième image:



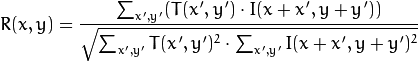
Plus la valeur de cette valeur est élevée, plus le modèle ressemble à la pièce correspondante dans la deuxième image. Avec OpenCV, cela peut être fait comme ceci:

 corr = cv2.matchTemplate(frame2, patch1, cv2.TM_CCORR_NORMED) plt.imshow(corr, cmap='gray'); 

Plus de détails peuvent être trouvés dans [7].

Le résultat est le suivant:



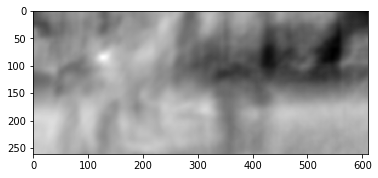
Nous voyons un pic clair, indiqué en blanc. Trouvez-le dans le deuxième cadre:

 min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(corr) h, w, _ = patch1.shape top_left = max_loc bottom_right = (top_left[0] + w, top_left[1] + h) frame2_copy = frame2.copy() cv2.rectangle(frame2_copy, top_left, bottom_right, 255, 2) plt.imshow(frame2_copy); 

Nous voyons que le pied a été trouvé correctement, selon ces données, nous pouvons comprendre dans quelle direction il s'est déplacé de la première image à la seconde et calculer le flux optique correspondant. De plus, il s'avère que cette opération est assez résistante aux distorsions photométriques, c'est-à-dire si la luminosité dans la deuxième image augmente fortement, le pic de corrélation croisée entre les images restera en place.

Compte tenu de tout ce qui précède, les auteurs ont décidé d'introduire la soi-disant couche de corrélation dans leur architecture, mais il a été décidé de ne pas considérer la corrélation en fonction des images d'entrée, mais en fonction des cartes de caractéristiques après plusieurs couches de l'encodeur. Une telle couche, pour des raisons évidentes, n'a pas de paramètres d'apprentissage, bien qu'elle soit essentiellement similaire à la convolution, mais au lieu de filtres, nous utilisons ici non pas des poids, mais une partie de la deuxième image:



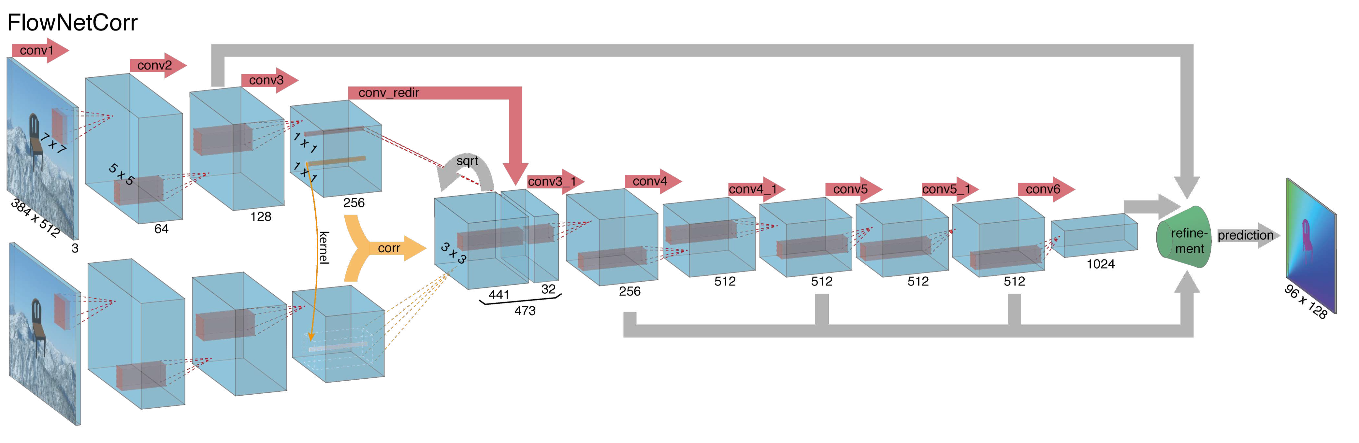
Curieusement, cette astuce n'a pas permis d'améliorer considérablement la qualité des auteurs de cet article, mais elle a été appliquée avec plus de succès dans d'autres travaux, et dans [9], les auteurs ont pu montrer qu'en modifiant légèrement les paramètres de formation, FlowNetC pouvait fonctionner beaucoup mieux.

Les auteurs ont résolu le problème de l'absence d'un ensemble de données d'une manière assez élégante: ils ont gratté 964 images de Flickr sur les thèmes: "ville", "paysage", "montagne" dans la résolution de 1024 × 768 et ont utilisé leur recadrage 512 × 384 comme arrière-plan, ce qui en a ensuite jeté quelques chaises à partir d'un ensemble ouvert de modèles 3D rendus. Ensuite, diverses transformations affines ont été appliquées indépendamment aux chaises et à l'arrière-plan, qui ont été utilisées pour générer la deuxième image d'une paire et le flux optique entre elles. Le résultat est le suivant:





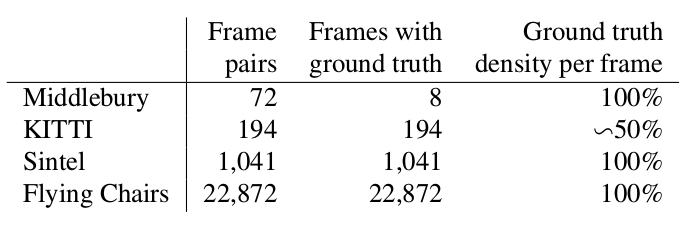
Un résultat intéressant a été que l'utilisation d'un tel ensemble de données synthétiques a permis d'obtenir une qualité relativement bonne pour les données d'un autre domaine. Le réglage fin des données correspondantes a bien sûr prouvé plus de qualités (+ ft dans le tableau ci-dessous):



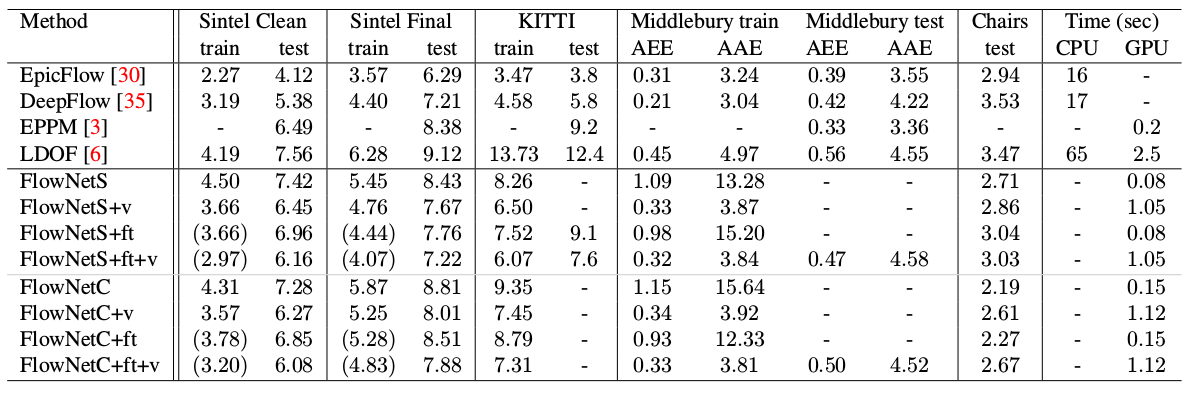
Le résultat sur de vraies vidéos peut être vu ici:

SpyNet (2016)

Dans de nombreux articles ultérieurs, les auteurs ont tenté d'améliorer la qualité en résolvant le problème de la mauvaise reconnaissance des mouvements brusques. Intuitivement, le mouvement ne sera pas capturé par le réseau si son vecteur dépasse considérablement le champ récepteur d'activation. Il est proposé de résoudre ce problème en raison de trois choses: une plus grande convolution, des pyramides et une «déformation» d'une image d'une paire en un flux optique. Tout est en ordre.

Donc, si nous avons quelques images dans lesquelles l'objet s'est fortement déplacé (10+ pixels), nous pouvons simplement réduire l'image (de 6 fois ou plus). La valeur absolue de l'offset diminuera de manière significative, et le réseau sera plus susceptible de «l'attraper», surtout si ses convolutions sont plus grandes que l'offset lui-même (dans ce cas, des convolutions 7x7 sont utilisées).



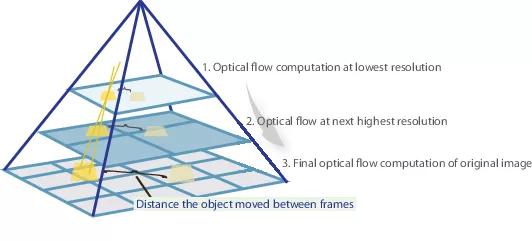
Cependant, lors de la réduction de l'image, nous avons perdu beaucoup de détails importants, nous devons donc passer au niveau suivant de la pyramide, dans lequel la taille de l'image est déjà plus grande, tout en tenant compte des informations que nous avons reçues auparavant lorsque nous avons calculé le flux optique à une taille plus petite. Cela se fait à l'aide de l'opérateur de déformation, qui raconte la première image en fonction de l'approximation disponible du flux optique (obtenue au niveau précédent). Une amélioration dans ce cas est que la première image qui est «poussée» selon l'approximation du flux optique sera plus proche de la seconde que l'originale, c'est-à-dire que nous réduisons encore la valeur absolue du flux optique, que nous devons prédire (rappel, petite valeur) les mouvements sont détectés beaucoup mieux, car ils sont complètement inclus dans une seule convolution). Du point de vue des mathématiques, ayant une image bitmap I et une approximation du flux optique V, l'opérateur de déformation peut être décrit comme suit:

$$

$$w (I, V) = I_w, \; \; I_w (x) = I (x + V (x)),$$

où $$$x = (i, j)$, c'est-à-dire un point spécifique de l'image $$$I$- l'image elle-même $$$V$- flux optique $$$I_w$- l'image résultante, "enveloppée" dans le flux optique.

Comment appliquer tout cela dans l'architecture CNN? Nous fixons le nombre de niveaux de pyramide $$$k$et un facteur par lequel chaque image suivante est réduite à un niveau à partir de la dernière $$$n$. Désigner par $$$d (*)$et $$$u (*)$les fonctions de sous-échantillonnage et de suréchantillonnage de l'image ou du flux optique par ce facteur.

Nous aurons également un ensemble de CNN-ok { $$$G_0 ... G_k$}, un pour chaque niveau de la pyramide. Alors $$$G_i$-le réseau acceptera quelques images avec $$$i$niveau de la pyramide et flux optique calculés sur $$$G_ {i-1}$niveau ( $$$G_0$acceptera simplement un tenseur de zéros à la place). Dans ce cas, nous enverrons l'une des images à la couche de déformation pour réduire la différence entre elles, et nous ne prédirons pas le flux optique à ce niveau, mais la valeur qui doit être ajoutée au flux optique augmenté (suréchantillonné) du niveau précédent pour obtenir le flux optique à ce niveau. Dans la formule, cela ressemble à ceci:

$$

$$v_k = G_k (I_k ^ 1, w (I_k ^ 2, u (V_ {k-1})), V_ {k-1})$$

Pour obtenir le flux optique lui-même, nous ajoutons simplement le prédicat de réseau et le flux accru du niveau précédent:

$$

$$V_k = u (V_ {k-1}) + v_k.$$

Pour obtenir la vérité sur le terrain pour le réseau à ce niveau, nous devons faire l'opération inverse - soustraire le prédicat de la cible (réduit au niveau souhaité) du niveau précédent de la pyramide. Schématiquement, cela ressemble à ceci:



L'avantage de cette approche est que nous pouvons enseigner chaque niveau indépendamment. Les auteurs ont commencé la formation à partir du niveau 0, chaque réseau suivant a été initialisé avec les paramètres du précédent. Depuis chaque réseau $$$G_i$résout le problème beaucoup plus simple que le calcul complet du flux optique dans une grande image, alors les paramètres peuvent être rendus beaucoup moins. À tel point que désormais l'ensemble peut tenir sur des appareils mobiles:



L'ensemble lui-même est le suivant (un exemple de pyramide à 3 niveaux):



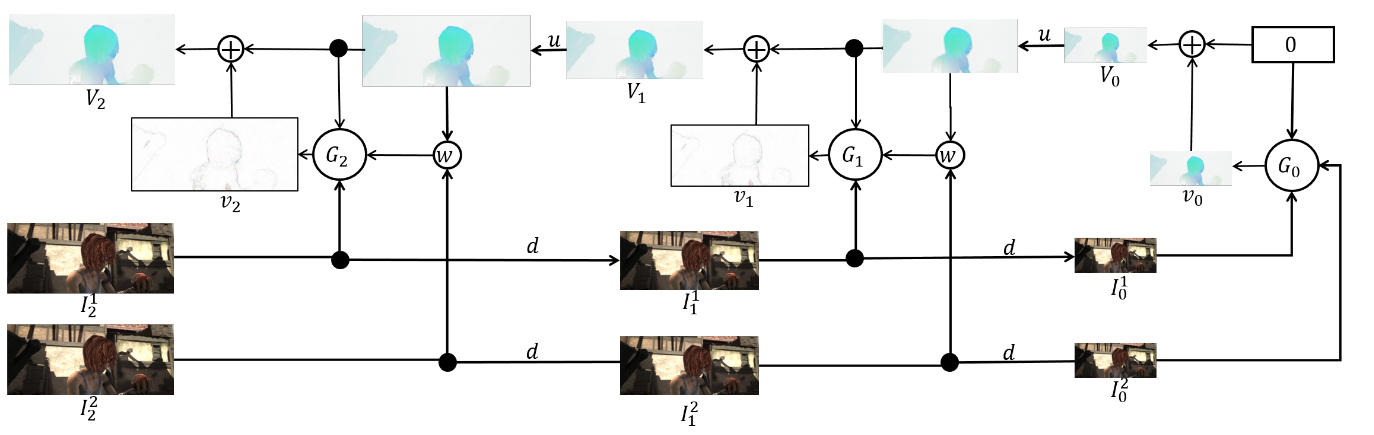
Reste à parler directement de l'architecture $$$G_i$réseau et faire le point. Chaque réseau $$$G_i$se compose de 5 couches convolutives, chacune se terminant par une activation ReLU, à l'exception de la dernière (qui prédit le flux optique). Le nombre de filtres sur chaque couche est respectivement { $$ }. Les entrées du réseau neuronal (l'image, la deuxième image «enveloppée» dans le flux optique et le flux optique lui-même) concaténent simplement en fonction de la dimension des canaux, leur tenseur d'entrée en a donc 8. Les résultats sont impressionnants:

PWC-Net (2018)

Inspirés par le succès de leurs collègues allemands, les gars de NVIDIA ont décidé d'appliquer leur expérience (et leurs cartes vidéo) pour améliorer encore le résultat. Leur travail était largement basé sur les idées du modèle précédent (SpyNet), donc PWC-Net traitera également des pyramides, mais des pyramides à convolution, pas des images originales, cependant, encore une fois - dans l'ordre.

L'utilisation d'intensités de pixels bruts pour calculer le flux optique n'est pas toujours raisonnable, car Un changement brusque de luminosité / contraste brisera notre hypothèse selon laquelle les pixels se déplacent d'une image à l'autre sans changements et l'algorithme ne sera pas résistant à de tels changements. Dans les algorithmes classiques de calcul du flux optique, diverses transformations sont utilisées pour atténuer cette situation, dans ce cas, les auteurs ont décidé de donner au modèle la possibilité d'apprendre de telles transformations. Par conséquent, au lieu de la pyramide d'images dans PWC-Net, des pyramides à convolution sont utilisées (d'où la première lettre dans Pwc-Net), c'est-à-dire il suffit de mettre en correspondance des cartes de différentes couches CNN, ce qui s'appelle ici un extracteur de pyramides d'objets.

Ensuite, tout est presque comme dans SpyNet, juste avant de soumettre à CNN, qui est appelé estimateur de flux optique, tout ce dont vous avez besoin, à savoir:

• image (dans ce cas, une carte d'entités de l'extracteur de pyramides d'entités),
• le flux optique suréchantillonné calculé au niveau précédent,
• la deuxième image, "enveloppée" (rappelez-vous la couche de déformation, donc la deuxième lettre dans pWc-Net) dans ce flux optique,

entre le deuxième cadre «enveloppé» et le premier habituel (encore une fois, je vous rappelle qu'au lieu d'images brutes, des cartes de caractéristiques avec extracteur de pyramides de fonctions sont utilisées ici), considérez ce qu'on appelle le volume des coûts (d'où la troisième lettre dans pwC-Net) et qui est essentiellement déjà précédemment considéré comme une corrélation entre deux images.



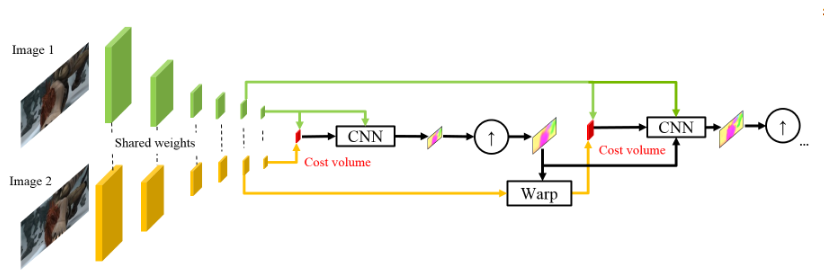
La touche finale est le réseau de contexte, qui est ajouté immédiatement après l'estimateur de flux optique et joue le rôle de post-traitement formé pour le flux optique calculé. Les détails architecturaux peuvent être consultés sous le spoiler ou dans l'article d'origine.


Les résultats sont encore plus impressionnants:



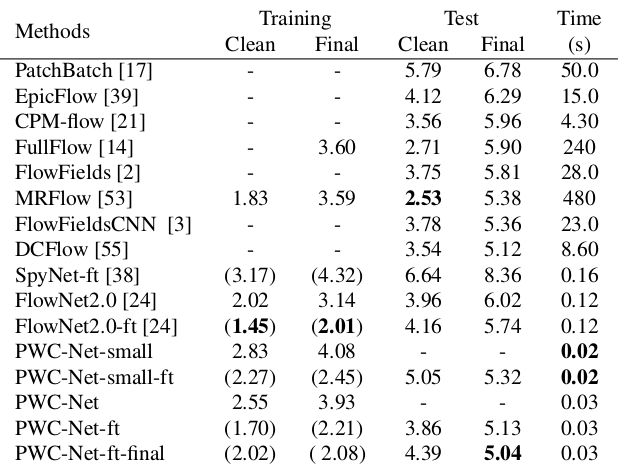
Comparé aux autres méthodes CNN de calcul du flux optique, PWC-Net réalise un équilibre entre la qualité et le nombre de paramètres:



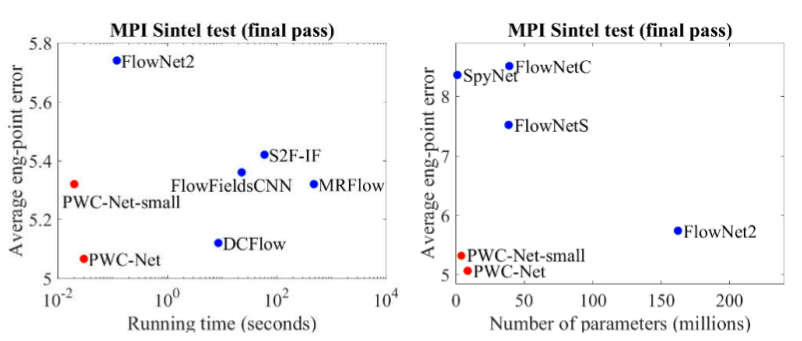
Il y a aussi une excellente présentation par les auteurs eux-mêmes, dans laquelle ils parlent du modèle lui-même et de leurs expériences:

Conclusion

L'évolution des architectures qui résolvent le problème du comptage de flux optique est un merveilleux exemple de la façon dont les progrès dans les architectures CNN et leur combinaison avec des méthodes classiques donnent le meilleur et le meilleur résultat. Et tandis que les méthodes CV classiques gagnent encore en qualité, les résultats récents donnent l'espoir que cela peut être résolu ...

Sources et liens

1. FlowNet: apprentissage du flux optique avec les réseaux convolutionnels: article , code .
2. Flux optique à grand déplacement: correspondance des descripteurs dans l'estimation du mouvement variationnel: article .
3. Estimation du flux optique à l'aide d'un réseau de pyramides spatiales: article , code .
4. PWC-Net: CNN pour le flux optique utilisant la pyramide, la déformation et le volume des coûts: article , code .
5. Ce que vous vouliez savoir sur le flux optique, mais avez été gêné de demander: article .
6. Calcul du flux optique par la méthode Lucas-Canada. Théorie: article .
7. Correspondance de modèle avec OpenCVP: dock .
8. Quo Vadis, reconnaissance d'action? Un nouveau modèle et l'ensemble de données cinétique: article .
9. FlowNet 2.0: évolution de l'estimation du flux optique avec les réseaux profonds: article , code .