👨🏼‍🚒 ✊🏼 🍩 Presque le canal MIMO le plus simple avec décoloration (modèle Kronecker inclus) 🛀🏾 ♑️ 🥅

Bonne journée à tous!

En ce qui concerne le thème de la diversité spatiale , nous avons déjà abordé les problèmes de décoloration dans les canaux de communication et pourquoi une telle décoloration se produit. Aujourd'hui, je propose de parler de ce sujet plus en détail.

De plus, dans l'article d'aujourd'hui, nous aborderons légèrement les questions de corrélation spatiale des canaux MIMO, qui sont traditionnellement discutées au cours du cours Communications mobiles ( CSP ) du professeur Haardt , et donc, à mon avis, une telle publication ne sera pas superflue. Et, je note tout de suite, l'éventail des problèmes ne se limite pas à une utilisation uniquement dans les communications mobiles.

En général, j'invite tous ceux qui s'intéressent au sujet des communications sans fil à lire, et c'est parti!

Colin Slater "Fading memories" . Oui, tout réduire à un seul sujet est probablement exagéré, mais avec une telle métaphore, je pense que vous pouvez imaginer ce que le récepteur reçoit après toutes sortes d'influences sur l'original, le signal d'information ...

De quoi parle-t-on?

Commençons par le fait que dans la nature il y a ce que l'on appelle des bruits multiplicatifs qui affectent la puissance du signal reçu - la décoloration .

Les termes, comme vous l'avez peut-être deviné, ne sont pas traduits directement en russe et en anglais, mais ce n'est pas très important.

Dans la littérature anglaise, le terme de décoloration implique une certaine influence qui, pour ainsi dire, fait que notre signal s'estompe, se "décolore".

Dans notre littérature, le terme évanouissement est généralement utilisé, et cela est principalement dû à l'effet de la propagation par trajets multiples: si une onde électromagnétique rencontre sa copie générée par les réflexions et la diffraction, et qu'elles sont en antiphase, les ondes s'annuleront - c'est-à-dire, le canal , pour ainsi dire, se fige .

La décoloration est rapide et lente (décoloration rapide et lente ).

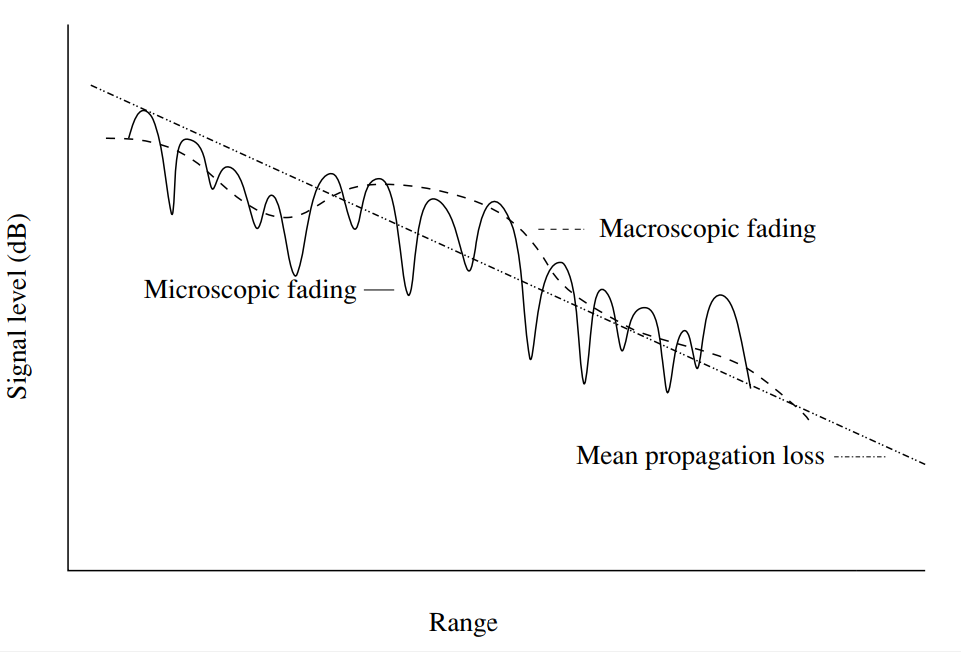
Fig. 1. Fluctuations de la puissance du signal dans les canaux sans fil en fonction de la distance. Le niveau moyen de perte de propagation augmente de façon monotone avec l'augmentation de la portée. Des écarts locaux peuvent survenir en raison de la décoloration macroscopique (lente) et microscopique (rapide) [1, p.14].

J'avoue tout de suite, aujourd'hui nous ne travaillerons pas avec une décoloration lente, mais nous parlerons des décolorations rapides avec suffisamment de détails.

Fig. 2. Illustration de l'effet d'ombrage: en règle générale, une décoloration lente se produit en raison de l'ombrage (ombrage). Pour la simulation, la distribution lognormale est généralement choisie.

Si vous voulez lire un peu sur la décoloration lente, en particulier, et sur la façon de simuler les chaînes satellite, en général, je vous invite ici !

Décoloration rapide

La décoloration rapide se produit, en règle générale, pour deux raisons principales:

en raison de la propagation par trajets multiples que nous avons déjà mentionnée et / ou
en raison des décalages de fréquence Doppler .

Ces derniers sont très visibles pour les systèmes à satellites , mais ils ne sont pas toujours pris en compte pour les cas de communications terrestres du fait que les stations de base dans ce cas sont généralement stationnaires.

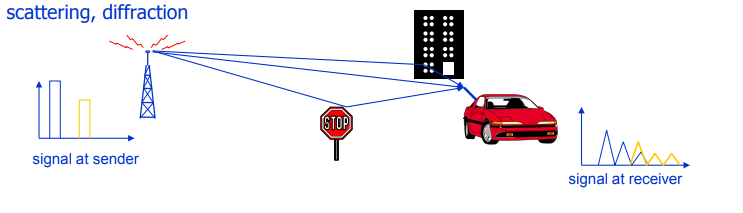
Fig. 3. Illustration des causes de la décoloration. Une attention particulière est portée à la diffusion et à la diffraction: c'est précisément à cause de ces phénomènes que la propagation dite multi-trajets se forme, conduisant à des interférences intersymboles ( ISI ).

Mais c'est loin d'être tout.

Décoloration sélective vs Décoloration plate

Ci-dessus, nous avons divisé notre ingérence selon la nature de l'événement . Cependant, les interférences peuvent également être divisées par la nature de l'effet sur le signal transmis . Et ici, nous avons besoin du concept de sélectivité de canal.

Nous donnons une petite classification selon [1, p. 14-18]. Ainsi, une décoloration rapide peut être:

Sélectif
a. Sélectif en fréquence
b. Sélectif dans le temps
c. Spatialement sélectif (cela concerne la question des angles d'arrivée et de départ des ondes électromagnétiques - nous n'analyserons pas aujourd'hui cette question)
Plat - gravitant davantage vers la nature de la décoloration lente (oui, c'est un tel paradoxe)

Ce que le dernier terme implique est expliqué à l'opposé.

Premièrement, si la largeur du spectre du signal transmis par nous dépasse la largeur de bande cohérente du canal , alors ils disent que nous avons affaire à des interférences sélectives en fréquence.

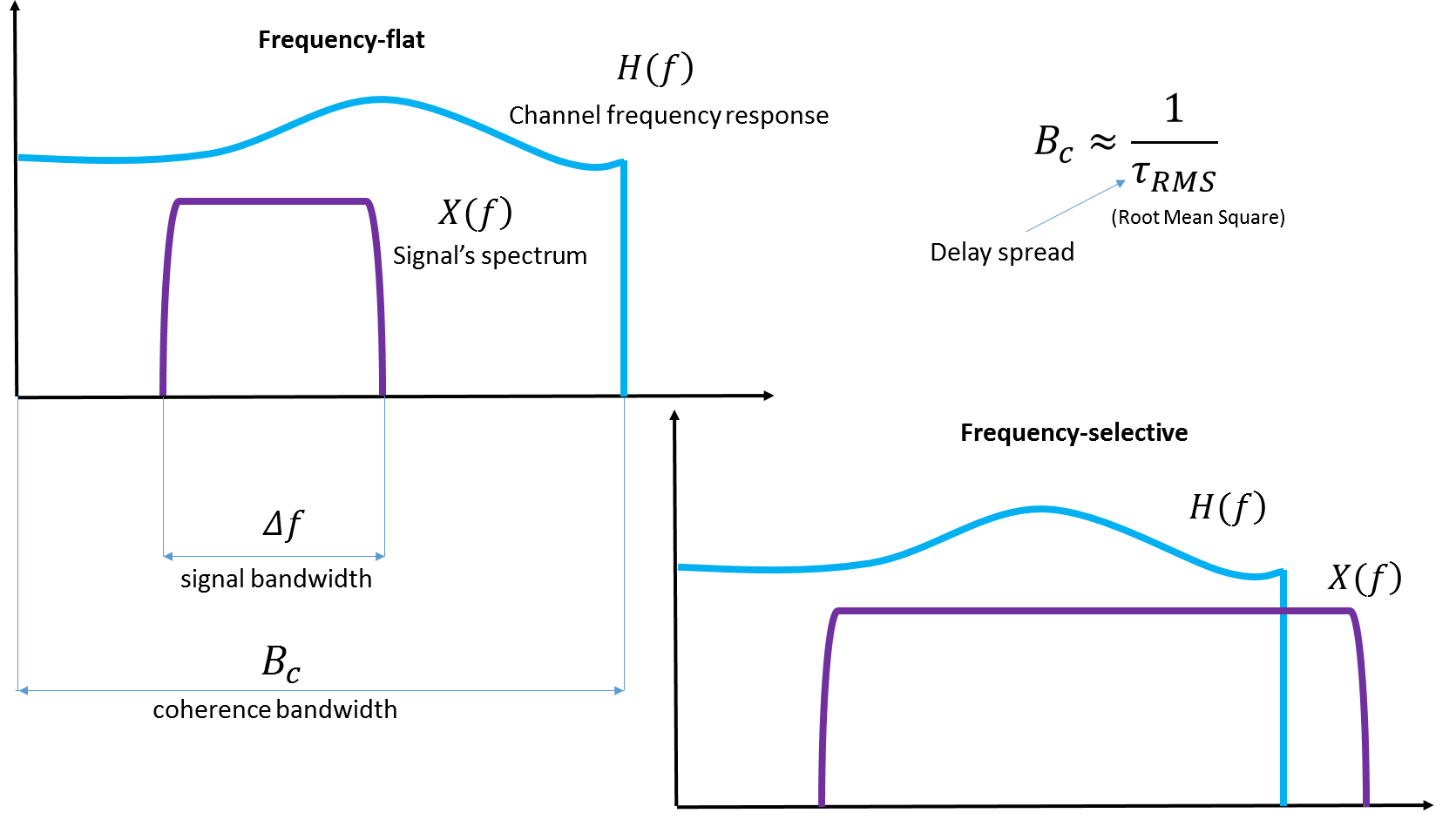
Fig. 4. Illustration d'une bande passante cohérente. Je pense que ce ne sera pas une mauvaise idée de joindre des illustrations de Wiki , s'il l'a lui-même ajouté.

Faites attention à l' écart de retard variable - la propagation des retards. C'est cet étalement des retards entre l'arrivée de différentes copies du même signal qui est mesuré lorsque les caractéristiques d'un canal réel particulier sont déterminées.

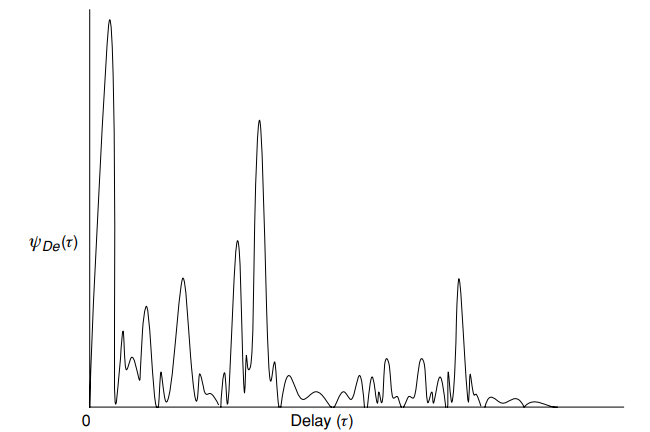
Fig. 5. Profil de retard (puissance) typique $\ psi_ {De} (\ tau)$ - puissance moyenne en fonction du retard $\ tau$ [1, p. 16]

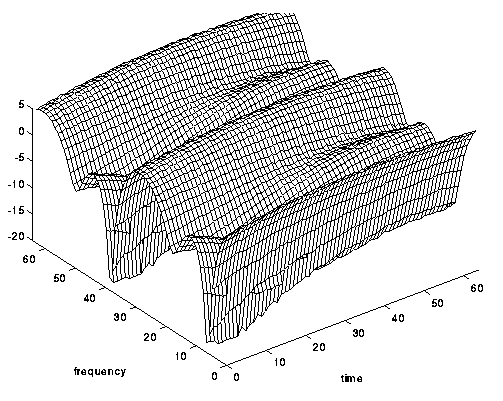
Fig. 6. Canal sélectif en fréquence, mais pas sélectif en fonction du temps .

Pour chaque plage, la bande cohérente sera différente.

Par exemple, pour la bande S (j'étais intéressé lorsque je cherchais des informations sur les systèmes à satellites) Bc = 0,5 - 2 MHz (Kanatas AG, Panagopoulos AD (éd.). Radio Wave Propagation and Channel Modeling for Earth - Space Systems. - CRC Press, 2016 . - p. 107).

Cela correspond très bien au débit en bauds , par exemple, d' un tel émetteur-récepteur satellite . Et il n'y a rien de surprenant: le débit de symboles des types linéaires de modulation numérique (PSK, QAM, OFDM) coïncide avec la bande occupée par le signal (voir Goldsmith A. Wireless communications . - Stanford University, 2004. - p. 140, 326), ce qui signifie ce serait bien d'essayer de presser le signal dans la bande cohérente au maximum. Les fréquences sont toujours une ressource précieuse.

Deuxièmement, si la longueur de notre signal dans le domaine temporel dépasse le temps de cohérence du canal , alors ils disent que nous avons affaire à un canal qui varie dans le temps.

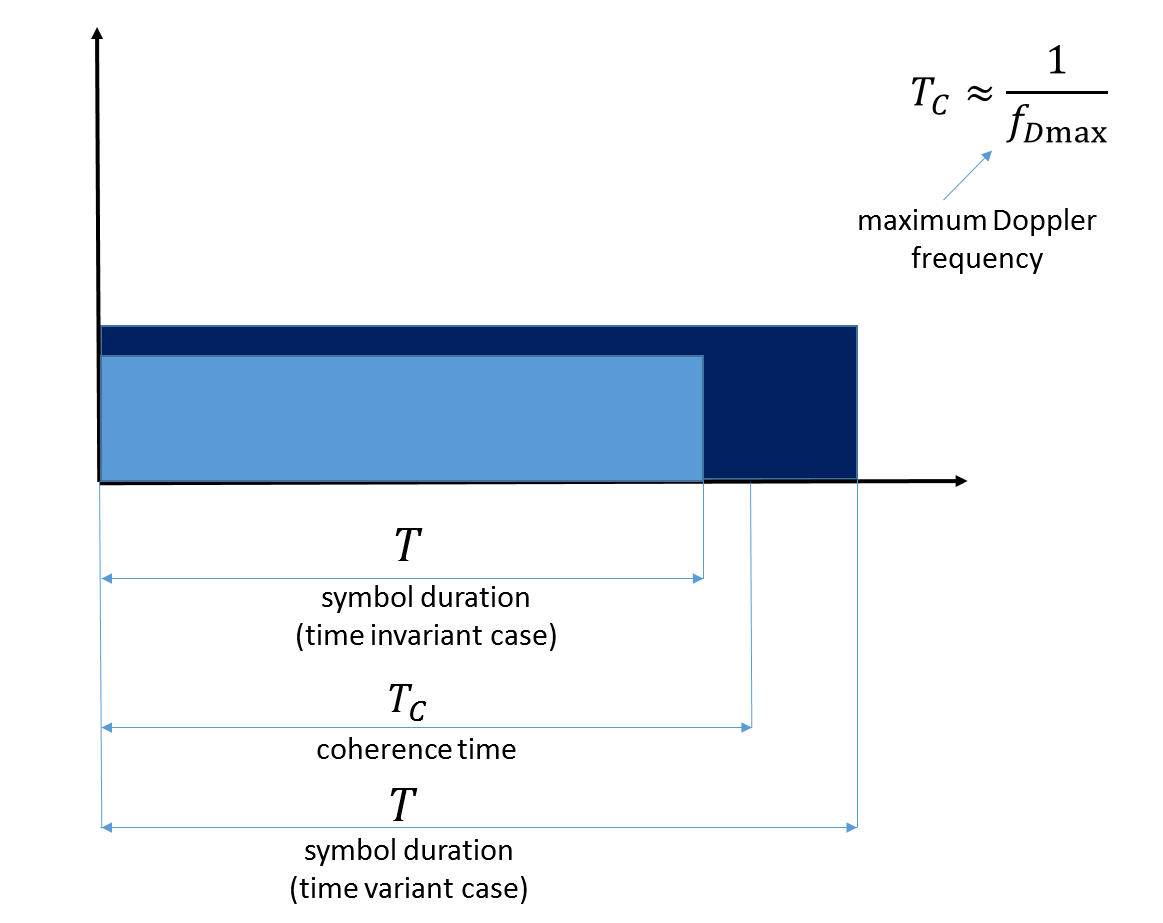
Fig. 7. Illustration du temps de cohérence. Veuillez noter qu'ici, la fréquence Doppler maximale reflète le mouvement du terminal mobile lui-même.

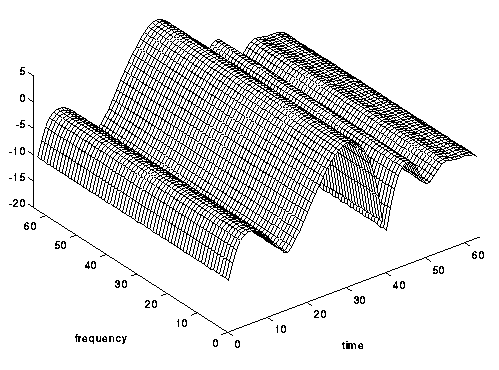
Fig. 8. Presque invisible dans le temps, mais sélective dans le temps: un canal en décomposition rapide.

Dans la vraie vie, malheureusement, il faut s'attendre aux deux.

Canal Rayleigh sélectif dans le temps et sélectif en fréquence; "La vraie situation."

Source de l'illustration: technologie sans fil Gigabit

Eh bien, et en conséquence, si nous parvenons à éviter ce qui précède, nous arriverons au cas le plus simple et le plus pratique - la décoloration plate [1, p. 14-18] [2, p. 88-92].

Le canal de fondu le plus simple

Vous avez peut-être déjà vu une manière similaire de simuler un canal plat qui s'estompe quelque part:

h = (1/sqrt(2))*(randn(size(msg)) + 1j*randn(size(msg))) % MatLab / Octave

Qu'est-ce que cela signifie:

manque de visibilité (cas justifié pour les communications terrestres)
canal à bande étroite (canal à bande étroite) - s'intègre dans la bande cohérente
- Soit dit en passant, nous avons considéré un exemple de canal à large bande dans cet article (Fig. 4).
il n'y a pas non plus de sélectivité en fréquence - s'intègre dans le temps cohérent
manque d'ombrage et décalages de fréquence Doppler

Autrement dit, il est ici en personne: un canal plat avec décoloration . Pour un boîtier sans ligne de visée, le canal est également appelé Rayleigh .

Lord Rayleigh

D'où vient un tel modèle?

Tout d'abord, en parlant des systèmes de communication modernes, nous entendons très probablement travailler avec des signaux numériques. De plus, nous travaillons aussi très probablement avec des types de modulation en quadrature ( I / Q ), c'est-à-dire avec des signaux complexes.

Fig. 9. La constellation de signaux QPSK . Coordonnées polaires, cercle unitaire. Par exemple, le symbole 11 correspondra à une coordonnée égale à environ 0,7 + 0,7i .

Il est logique de supposer l'effet de l'interférence sur la composante réelle et imaginaire. De plus, il vaut la peine de suivre le théorème de la limite centrale pour supposer également la nature gaussienne de tels effets. Nous écrivons la formule [1, p. 39]:

$Z = X + jY \ qquad (1)$

où $X \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ et $Y \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ Sont des variables aléatoires normalement distribuées.

Le plus souvent, un modèle avec une puissance moyenne normalisée est utilisé:

$var \ {Z \} = E \ {\ left | Z \ right | ^ 2 \} = 1 \ qquad (2)$

Et cela signifie $Z \ sim \ mathcal {N} (0, \, 1)$ .

Si nous supposons des distorsions indépendantes des composantes de l'enveloppe du signal: à la fois en phase ( I - en phase) et en quadrature ( Q - Quadrature), alors la position du nombre par lequel le symbole d'origine sera multiplié (d'où le bruit multiplicatif ), en coordonnées polaires, peut être calculé littéralement par le théorème de Pythagore:

$Z = \ sqrt {\ hat {X} ^ 2 + \ hat {Y} ^ 2} \ qquad (3)$

où $\ hat {X} \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ et $\ hat {Y} \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ - ce sont aussi des variables aléatoires normalement distribuées. Pour la puissance nominale $\ hat {X} \ sim \ mathcal {N} (0, \, 1)$ , $\ hat {Y} \ sim \ mathcal {N} (0, \, 1)$ .

Et nous avons ici la formule du processus de Rayleigh ! [2, p. 78]

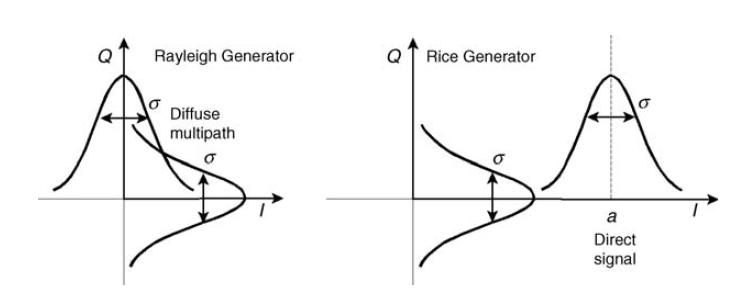
Fig. 10. Générateurs carrés gaussiens pour modéliser la décoloration de Rayleigh et Rice [3, p.125]. Nous parlerons de la chaîne Rice un peu plus tard.

Digression lyrique.

Personnellement, j'aime vraiment l'exemple avec le tir au canon : si deux canons tirent perpendiculairement l'un à l'autre un nombre suffisant de fois, alors pour chacun individuellement la distribution des coups sera normale, et la distribution totale des coups est Rayleigh. Quelque chose de similaire se produit avec notre interférence.

Si nous considérons le cas le plus simple sans aucune corrélation spatiale entre les canaux (disons que nous avons plusieurs canaux spatiaux - MIMO ), alors ils disent que le canal est spatialement blanc - spatialement blanc . Et comme tous les canaux sont indépendants, il est donc possible de «générer» non seulement des variables aléatoires réparties selon Rayleigh, mais aussi des vecteurs, des matrices et des tenseurs [3, p. 125]:

$\ mathbf {H} _ {NLoS} = \ sqrt {\ frac {1} {2}} \ left (\ mathbf {G} _1 + j \ mathbf {G} _2 \ right) \ qquad (4)$

où $\ mathbf {G} _1 \ sim \ mathcal {N} (0, \, 1)$ et $\ mathbf {G} _2 \ sim \ mathcal {N} (0, \, 1)$ Sont des matrices constituées de valeurs normalement distribuées.

D'où vient 1/2 sous la racine?

Tout est assez simple ici: comme nous l'avons dit plus haut, la puissance de réponse du canal doit être égale à l'unité, c'est-à-dire:

$P = E \ {hh ^ * \} = 1$

C'est pour cela que le facteur d'échelle est introduit $\ sqrt {\ frac {1} {2}}$ .

Démontrez (prenez python pour un changement):

 import numpy as np N = int(1e6) h = 1/np.sqrt(2)*(np.random.randn(N) + 1j*np.random.randn(N)) P = np.mean(h*np.conj(h)) print(np.round(P)) >>> (1+0j)

Pour résumer :
La composante d'interférence en l'absence de visibilité directe peut être décrite comme un vecteur à n dimensions (selon la dimension du canal) indépendant à distribution identique ( IID - indépendant à distribution identique) selon la loi gaussienne complexe avec symétrie circulaire et tapis nul. espérance ( ZMCSCG - Gaussien complexe à symétrie circulaire de moyenne nulle).

Un virelangue entier!

Presque le canal de fondu le plus facile

Et si la visibilité était toujours directe? Peut-être existe-t-il déjà des modèles mathématiques prêts à l'emploi sur cette partition?

Bien sûr qu'il y en a! Par exemple, ceci [4] , généralisé pour le cas avec plusieurs antennes de réception et d'émission (MIMO):

$\ mathbf {H} = \ sqrt {\ frac {K} {K + 1}} \ mathbf {H_ {LoS}} + \ sqrt {\ frac {1} {K + 1}} \ mathbf {H_ {NLoS} } \ qquad (5)$

où $$ \ mathbf {H}$ - il s'agit en fait de l'enveloppe complexe de la réponse impulsionnelle du canal (ou matrice de canal, si nous parlons de MIMO ), $$ \ mathbf {H_ {LoS}}$ Fait partie de la visibilité directe (ligne de visée), et $\ mathbf {H_ {NLoS}}$ - ceci est une composante du manque de visibilité directe (sans visibilité directe), nous l'avons déjà considéré.

Faites attention à la variable K - c'est ce qu'on appelle le facteur Rice (facteur Ricien / Ricain) - le rapport de la puissance du chemin de propagation directe à la puissance de tous les autres chemins. C'est lui qui détermine dans quelle mesure notre chaîne sera soumise à des interférences.

Stephen O. "Steve" Rice

Durée $\ sqrt {\ frac {K} {K + 1}} \ mathbf {H} _ {LoS} = E \ {H \}$ représente l'attente mathématique de la matrice de canaux et peut être modélisée en fonction de la géométrie des réseaux de réception et d'émission d'antennes:

$\ mathbf {H} _ {LoS} = \ mathbf {a} _R (\ theta_R) \ mathbf {a} _T (\ theta_T) ^ H \ qquad (6)$

où $\ mathbf {a} _R (\ theta_R)$ et $\ mathbf {a} _T (\ theta_T)$ - ce sont les réponses des réseaux de réception et d'émission d'antennes, respectivement, et $\ theta_R$ et $\ theta_T$ Sont les angles d'arrivée et de départ (angle de départ).

Les facteurs sont généralement symétriques et peuvent être décrits par la formule générale:

$\ mathbf {a} = \ left [1, e ^ {j2 \ pi d cos (\ theta)}, ..., e ^ {j2 \ pi d (N-1) cos (\ theta)} \ right] \ qquad (7)$

où $d$ Est la distance entre les antennes (espacement des antennes) en longueurs d'onde, et $N$ - c'est le nombre d'éléments dans le réseau d'antennes (Fig. 11).

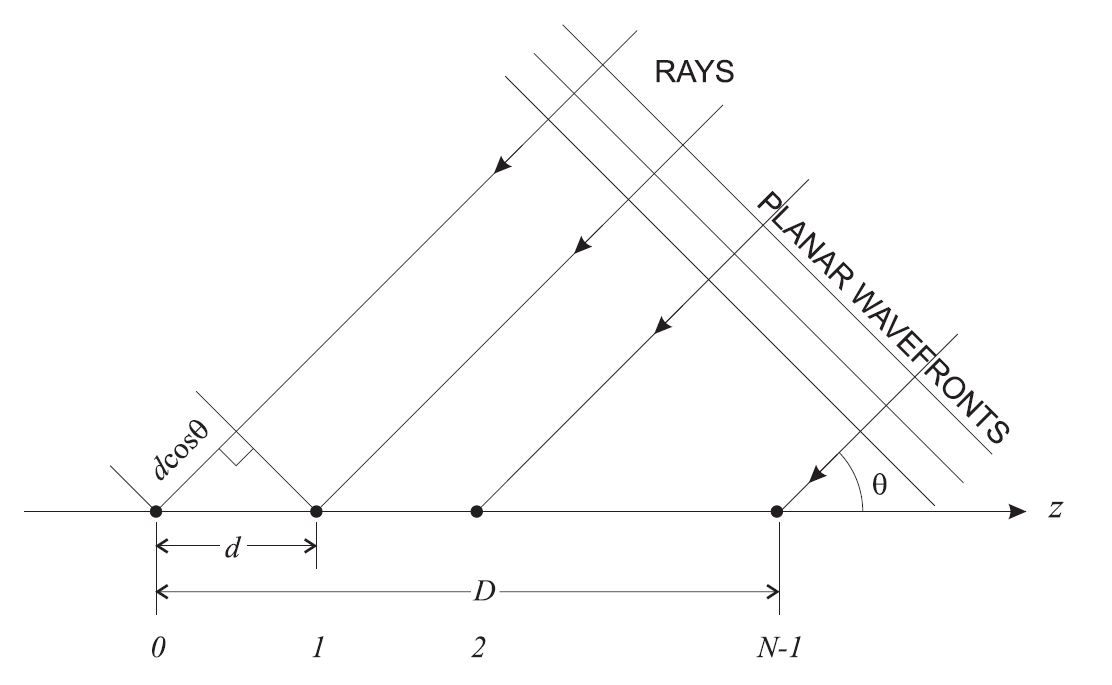
Fig. 11. La géométrie d'un réseau linéaire . Pour Massive MIMO, la géométrie sera bien sûr différente. Vous pouvez en savoir plus à ce sujet, par exemple ici .

Eh bien, maintenant que le modèle est au moins quelque peu démonté, vous pouvez le simplifier.

Pour le cas de SISO (le plus simple et le plus basique), la formule (5) prendra la forme:

$h = \ sqrt {\ frac {K} {K + 1}} + \ sqrt {\ frac {1} {2 (K + 1)}} \ left (G_1 + jG_2 \ right) \ qquad (8)$

pour pour 1 antenne d'émission et 1 antenne de réception $\ mathbf {a} _T (\ theta_T) \ mathbf {a} _R (\ theta_R) = 1$ .

Et cela, soit dit en passant, correspond au modèle de la figure 12.

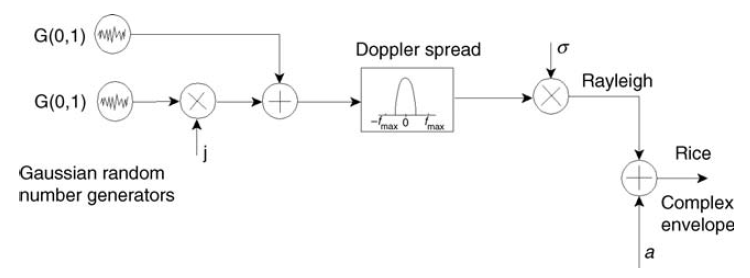
régime

Fig. 12. Le schéma de formation du canal de Rice (signal à bande étroite) [3, p.127]. À $K \ à 0$ le canal dégénérera de plus en plus en Rayleigh. C'est pourquoi j'ai utilisé le mot presque dans le sous-titre: le canal Rayleigh est un cas particulier du canal Rice. Cela ressort également de la formule (5).

Expliquons: $\ sigma = \ sqrt {\ frac {1} {2 (K + 1)}}$ Est le paramètre d'échelle ricienne, et $a = \ sqrt {\ frac {K} {K + 1}}$ Est un paramètre de non-centralité.

Si nous considérons le fondu plat, on suppose que le bloc Doppler Spread a une réponse de 1.

En général, dans le but de modéliser la propagation Doppler, vous rencontrerez très probablement un modèle Jakes (en forme de U) basé sur la technique de la somme des sinusoïdes . Théoriquement, le spectre d'un tel modèle ressemble à ceci:

La densité spectrale de puissance de l'atténuation de Rayleigh avec un décalage Doppler maximum de 10 Hz. Source

Cependant, dans la vie, à en juger par [1, p. 15] un tel spectre semble encore moins uniforme:

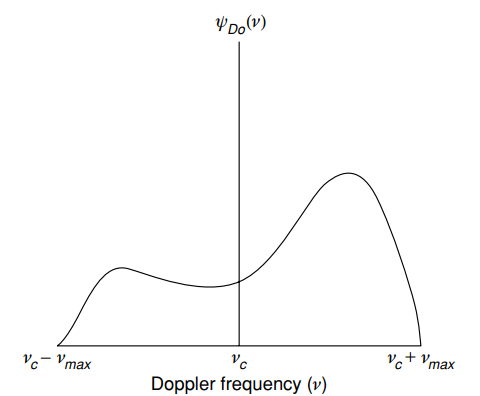
Spectre Doppler (énergie) typique $\ psi_ {Do} (v)$ - puissance moyenne en fonction de la fréquence Doppler $(v)$ [1, p. 15].

Attentes ... Réalité.

Il existe de tels schémas de combinaison avec une décoloration lente.

Par exemple, c'est pour le modèle Corazza-Vatalaro (C & V) :

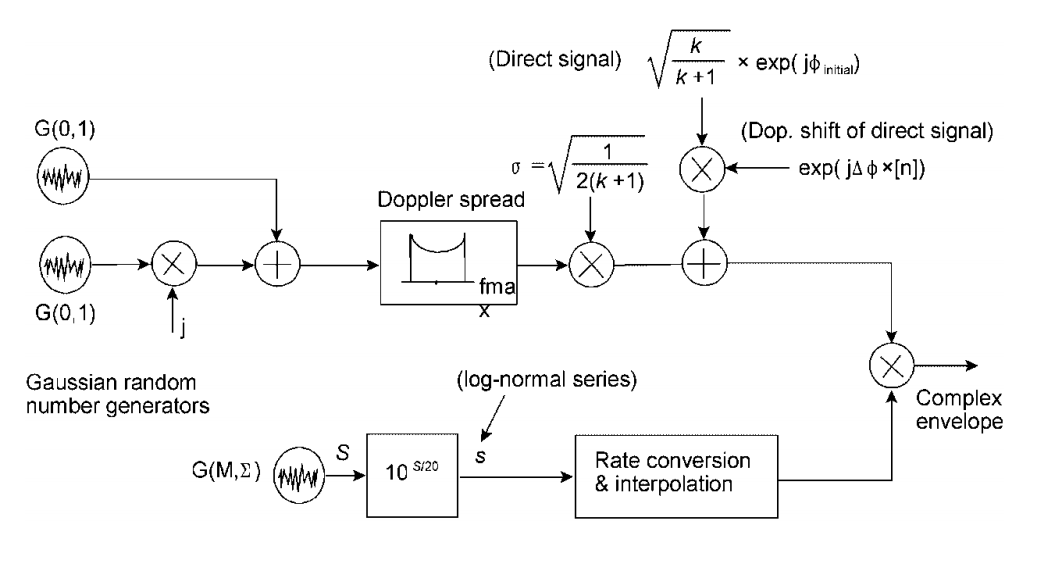
voir Fontan, FP, Mayo, A., Marote, D., Prieto - Cerdeira, R., Mariño, P., Machado, F., et Riera, N. (2008). Examen des modèles génératifs pour le canal de propagation par satellite mobile terrestre à bande étroite. Journal international des communications et des réseaux par satellite, 26 (4), 291-316.

Mais c'est une histoire complètement différente ...

Modéliser presque le canal d'évanouissement le plus facile dans MatLab

Comparons les calculs reçus avec quelque chose de déjà vérifié. Par exemple, avec des fonctions MatLab spéciales .

Pour tester le modèle, pour notre part, nous générons un message binaire aléatoire (la longueur du message est de 100 000 bits), le modulons à l'aide de M-PSK ou M-QAM , multiplions élément par élément le processus de décoloration, ajoutons du bruit gaussien blanc, égalisons l'égaliseur Zero-Forcing, démodulons et calculons taux d'erreur sur les bits (BER - taux d'erreur sur les bits) (Fig. 13). Le nombre de tests sera égal à cent.

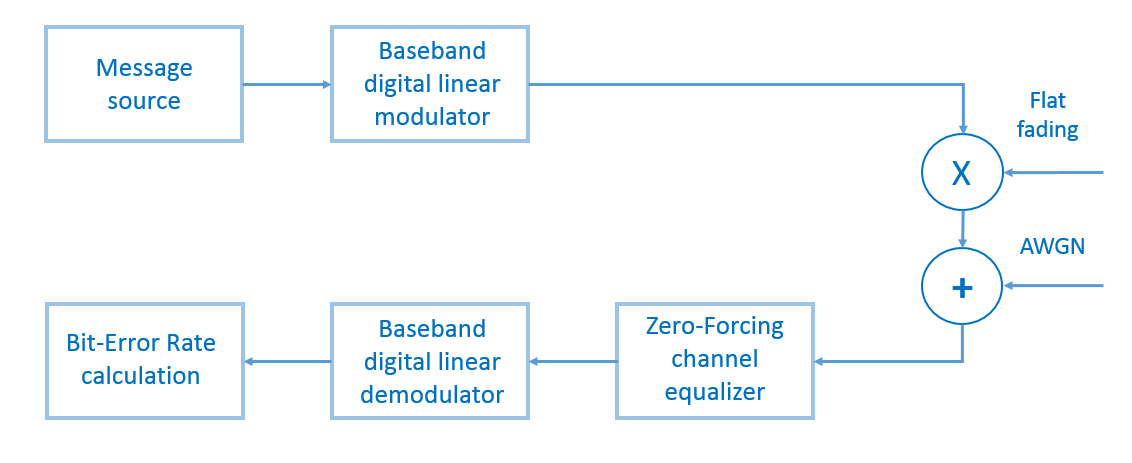
Fig.13. Le schéma de principe du modèle du système de transmission que notre script va décrire.

Le script peut être consulté ici.

Et téléchargez ici .

 clear all; close all; clc EbNo = 0:40; K = [4.0; 0.6]; M = [4; 8; 16; 64; 256]; %Positions of modulation (M-PSK or M-QAM) for k = 1:length(K) for m = 1:length(M) message = randi([0, M(m)-1], 100000, 1); if M(m) >= 16 mod_msg = qammod(message, M(m), pi/4, 'gray'); ric_ber(:, m, k) = berfading(EbNo,'qam',M(m),1,K(k)); else mod_msg = pskmod(message, M(m), pi/4, 'gray'); ric_ber(:, m, k) = berfading(EbNo, 'psk', M(m), 1, K(k)); end Es = mean(abs(mod_msg).^2); No = Es./((10.^(EbNo./10))*log2(M(m))); h = sqrt( K(k)/(K(k)+1)) +... sqrt( 1/(K(k)+1))*(1/sqrt(2))*(randn(size(mod_msg))... + 1j*randn(size(mod_msg))); ric_msg = mod_msg.*h; % Rician flat fading for c = 1:100 for jj = 1:length(EbNo) noisy_mod = ric_msg +... sqrt(No(jj)/2)*(randn(size(mod_msg))+... 1j*randn(size(mod_msg))); %AWGN noisy_mod = noisy_mod ./ h; % zero-forcing equalization if M(m) >= 16 demod_msg = qamdemod(noisy_mod, M(m), pi/4, 'gray'); else demod_msg = pskdemod(noisy_mod, M(m), pi/4, 'gray'); end [number,BER(c,jj)] = biterr(message,demod_msg); end end sum_BER(:,m, k) = sum(BER)./c; end end figure(1) semilogy(EbNo, sum_BER(:,1,1), 'b-o', EbNo, sum_BER(:,2,1), 'r-o',... EbNo, sum_BER(:,3,1), 'g-o', EbNo, sum_BER(:,4,1), 'c-o',... EbNo, sum_BER(:,5,1), 'k-o',... EbNo, ric_ber(:,1,1), 'b-', EbNo, ric_ber(:,2,1), 'r-',... EbNo, ric_ber(:,3,1), 'g-', EbNo, ric_ber(:,4,1), 'c-',... EbNo, ric_ber(:,5,1), 'k-', 'LineWidth', 1.5) title('Rician model (K = 4.0)') legend('QPSK(simulated)', '8-PSK(simulated)',... '16-QAM(simulated)', '64-QAM(simulated)' ,'256-QAM(simulated)',... 'QPSK(theory)','8-PSK(theory)', '16-QAM(theory)',... '64-QAM(theory)' ,'256-QAM(theory)','location','best') xlabel('EbNo (dB)') ylabel('BER') grid on figure(2) semilogy(EbNo, sum_BER(:,1,2), 'b-o', EbNo, sum_BER(:,2,2), 'r-o',... EbNo, sum_BER(:,3,2), 'g-o', EbNo, sum_BER(:,4,2), 'c-o',... EbNo, sum_BER(:,5,2), 'k-o',... EbNo, ric_ber(:,1,2), 'b-', EbNo, ric_ber(:,2,2), 'r-',... EbNo, ric_ber(:,3,2), 'g-', EbNo,ric_ber(:,4,2), 'c-',... EbNo, ric_ber(:,5,2), 'k-','LineWidth', 1.5) title('Rician model (K = 0.6)') legend('QPSK(simulated)', '8-PSK(simulated)',... '16-QAM(simulated)', '64-QAM(simulated)' ,'256-QAM(simulated)',... 'QPSK(theory)','8-PSK(theory)',... '16-QAM(theory)', '64-QAM(theory)' ,'256-QAM(theory)','location','best') xlabel('EbNo (dB)') ylabel('BER') grid on

Vous devriez obtenir quelque chose comme ceci:

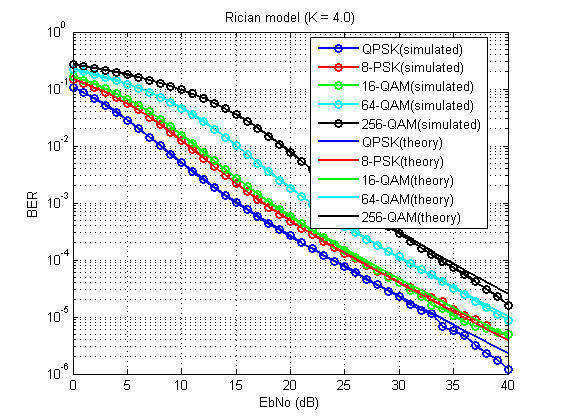
Fig. 14. Le coefficient des erreurs binaires pour le modèle considéré (K = 4,0).

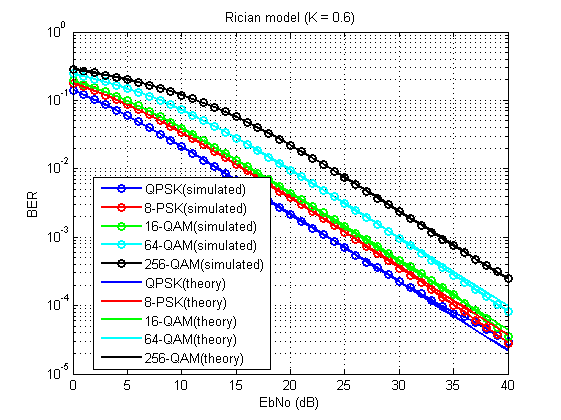
Fig. 15. Taux d'erreur sur les bits pour le modèle considéré (K = 0,6).

Pas sans défauts, bien sûr (en raison du nombre limité de moyennes), mais en général, on voit que ça marche!

D'accord, mais sera-t-il possible d'adapter l'expérience au cas du MIMO? Oui bien sûr.

Pour ce faire, nous faisons une hypothèse: la matrice des canaux sera constituée de chemins de propagation indépendants, chacun étant distribué selon Rice.

Dans quelles conditions est-ce possible?

Comme nous l'avons noté ci-dessus, le composant IID peut être généré dans n'importe quelle dimension. Cela signifie que tout canal MIMO spatialement blanc sans ligne de visée peut être modélisé comme un ensemble de canaux SISO (en fonction de la dimension du canal).

Avec le composant de ligne de visée un peu plus compliqué - vous devez prendre en compte la position des réseaux.

Considérons la formule (5): si notre matrice de la composante de la ligne de visée ne sera constituée que d'unités $\ mathbf {H} _ {LoS} = \ mathbf {1}$ , il semble que la composante de Raysov devienne également spatialement blanche.

Pour aborder cela, nous écrivons la composante de la ligne de visée plus en détail que dans la formule (6):

$\ mathbf {H} _ {LoS} = \ begin {bmatrix} 1 \\ \ exp (j2 \ pi dcos (\ theta_R)) \\. \\. \\. \\ \ exp (j (M_R-1) 2 \ pi dcos (\ theta_R)) \ end {bmatrix} \ begin {bmatrix} 1 & \ exp (j2 \ pi dcos (\ theta_T)) &. &. &. & \ exp (j (M_T-1) 2 \ pi dcos (\ theta_T)) \ end {bmatrix}$

Il est frappant de constater que si $\ theta_R = \ theta_T = 90 ^ o$ , alors la matrice sera composée d'une unité. Géométriquement, il s'agit d'une situation où deux tableaux d'éléments sont strictement orientés l'un vers l'autre:

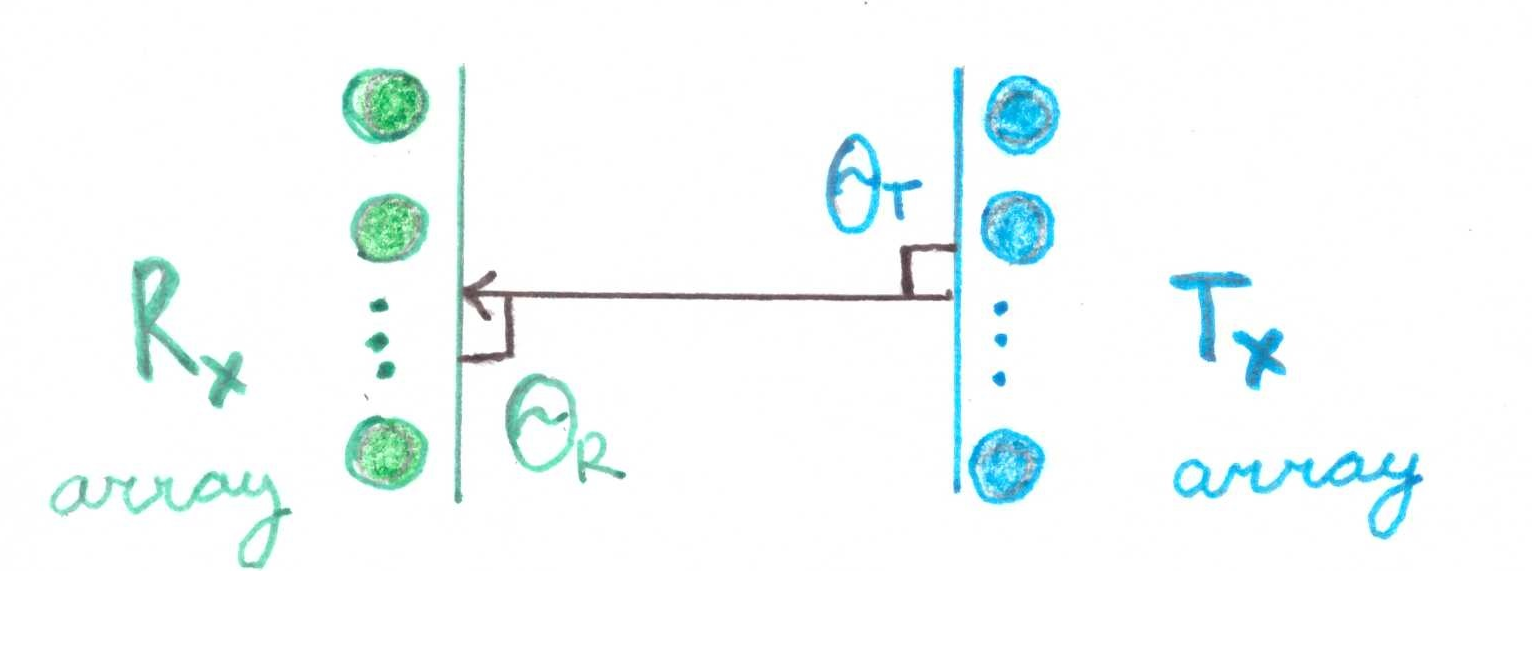
Faisons une petite démonstration mathématique:

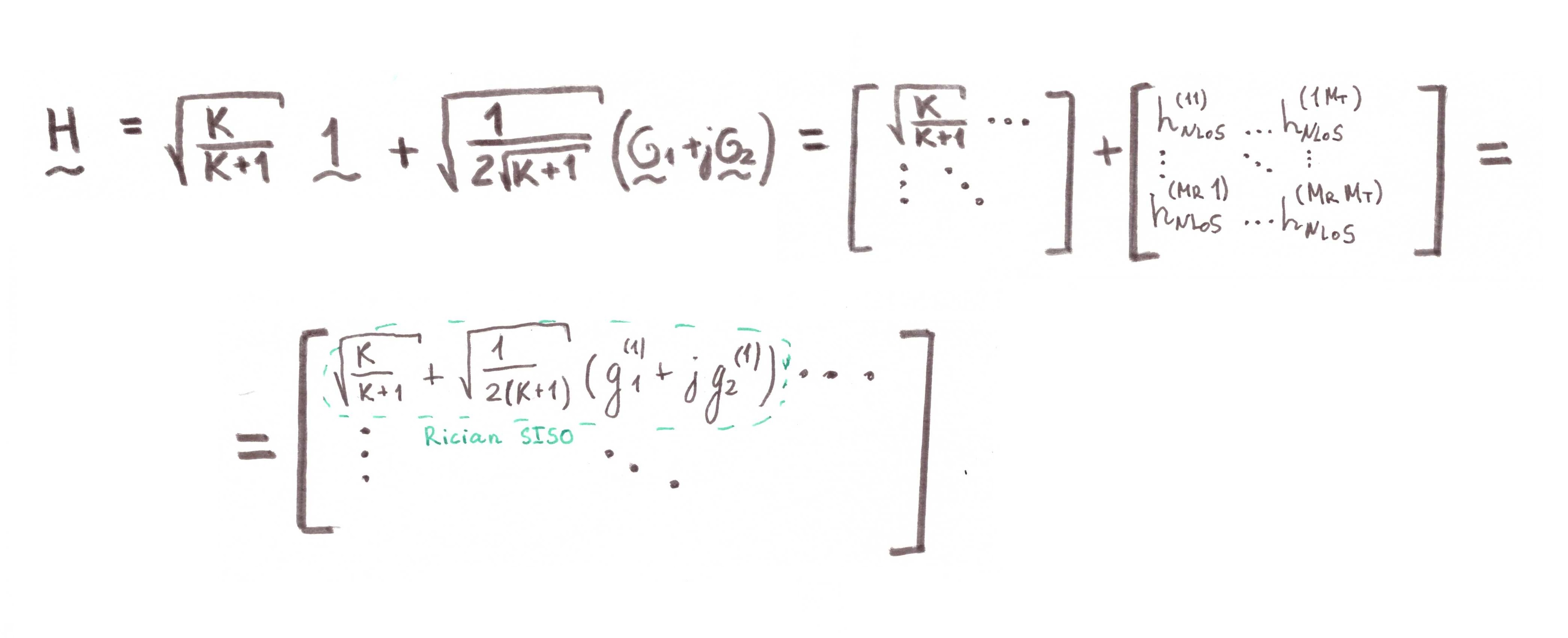
Pour la modélisation, nous prenons le schéma d'Alamouti comme base. Il devrait en résulter quelque chose comme ceci:

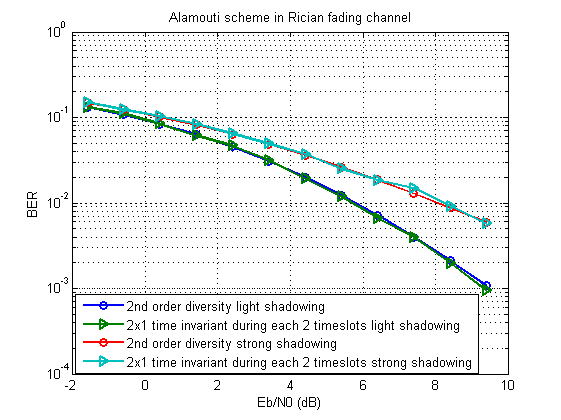
Le script étendu peut être téléchargé ici .

Bravo.

Presque le canal d'évanouissement et la corrélation spatiale les plus faciles

Et maintenant, en terminant notre voyage dans le monde des calculs statistiques, rapprochons-nous un peu de la réalité.

Ci-dessus, nous avons considéré le cas où la composante de l'absence de ligne de visée était spatialement blanche . Cependant, à partir de systèmes réels, il faut encore s'attendre à une certaine corrélation entre les antennes, et donc entre les trajets de propagation de l'onde EM.

Nous introduisons une nouvelle variable - la matrice de corrélation spatiale:

$\ mathbf {R} = E \ {vec (\ mathbf {H}) vec (\ mathbf {H}) ^ H \} \ qquad (8)$

où vec désigne une opération de vectorisation . Soit dit en passant, cette matrice n'affectera que la composante du manque de ligne de vue , et donc dans ce cas $\ mathbf {H} = \ mathbf {H} _ {NLoS}$ .

Exemple pour MIMO 2x2

Il est raisonnable de supposer que dans la vie réelle, cette matrice est d'abord déterminée par des mesures, puis seulement elles sont utilisées pour la modélisation:

$vec (\ mathbf {H} _ {NLoS}) = \ mathbf {R} ^ {1/2} vec (\ mathbf {H} _w) \ qquad (9)$

où $\ mathbf {H} _w$ Est la matrice IID ( w signifie spatialement w hite).

Notez que l'élévation d'une matrice à une puissance n'est pas une élévation à une puissance de chacun de ses éléments. Par conséquent, dans notre cas, la fonction sqrt () ne peut pas être utilisée dans MatLab . Utilisez l'opérateur ^ .
Pour Python, vous ne pouvez pas utiliser l'opérateur exponentiation ** et la méthode sqrt du module numpy populaire. Vous devez utiliser la méthode fractional_matrix_power du module scipy .

Si le récepteur et l'émetteur sont suffisamment indépendants l'un de l'autre, comme sur la figure 16, alors le modèle de Kronecker peut être appliqué [1, p. 40], pour réduire le nombre de coefficients de calcul:

$\ mathbf {R} = \ mathbf {R} ^ T_T \ otimes \ mathbf {R} _R \ qquad (10)$

où $\ otimes$ désigne une œuvre de Kronecker .

Léopold Kronecker

Nous considérons séparément les composants de la matrice d'expression:

$\ mathbf {R} _R = \ frac {1} {M_T} E \ left \ {\ left (\ mathbf {H} _ {NLoS} \ mathbf {H} ^ H_ {NLoS} \ right) ^ T \ right \ }$ Est la matrice de corrélation des antennes de réception,

$\ mathbf {R} _T = \ frac {1} {M_R} E \ left \ {\ mathbf {H} ^ H_ {NLoS} \ mathbf {H} _ {NLoS} \ right \}$ Est la matrice de corrélation des antennes d'émission

$M_R$ et $M_T$ - c'est le nombre d'antennes de réception et d'émission, respectivement. Les deux matrices sont des matrices hermitiennes semi-définies positives. De plus, le rang de la matrice $\ mathbf {H} _ {NLoS}$ limité par la valeur $min (rang (\ mathbf {R} _T), rang (\ mathbf {R} _R))$ .

Fig. 16.
Modèle de diffuseurs dans le cas d'un récepteur et émetteur non corrélés. Les points verts signifient les diffuseurs, le bleu et le rouge signifient le récepteur et l'émetteur. Je m'excuse pour la qualité, ceci est une capture d'écran d'un des devoirs de TU Ilmenau.

Dans ce cas, la matrice des canaux peut s'écrire:

$\ mathbf {H} = \ sqrt {\ frac {K} {K + 1}} \ mathbf {H} _ {LoS} + \ sqrt {\ frac {1} {K + 1}} \ mathbf {R} ^ {1/2} _R \ mathbf {H} _ {w} \ left (\ mathbf {R} ^ {1/2} _T \ right) ^ H \ qquad (11)$

Cependant, pour des situations telles que, par exemple, dans la figure 17, vous devez toujours utiliser la matrice de corrélation complète (voir formule (9)).

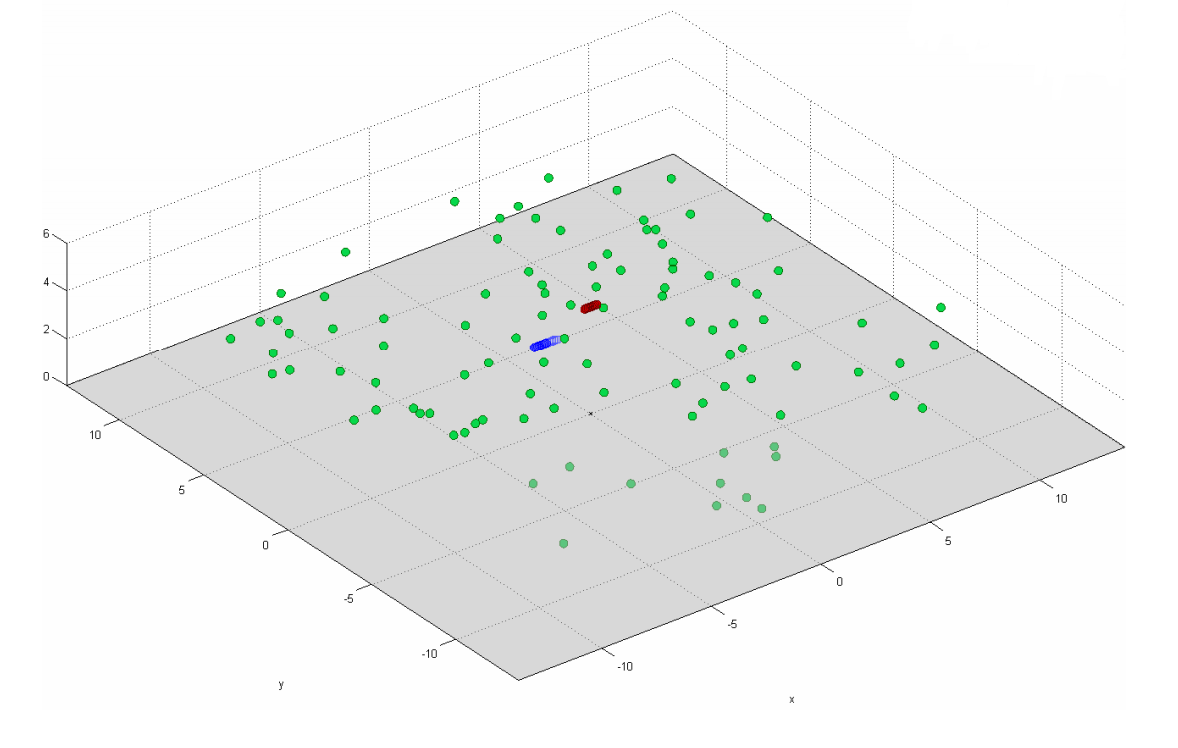
Fig. 17. Modèle de diffuseurs dans le cas de corrélation récepteur et émetteur. Les points verts signifient les diffuseurs, le bleu et le rouge signifient le récepteur et l'émetteur.

Afin de consolider ce que nous avons appris et de voir comment la corrélation spatiale complique la vie, essayons de calculer la bande passante des canaux. Par exemple, pour MIMO 2x2.

Pour ce faire, nous prenons les cas suivants (nous entendons tout de même le fondu plat, pour plus de simplicité nous ne considérons également que le canal de Rayleigh):

1) Canal spatialement blanc;
2) Modèle de Kronecker avec une corrélation relativement faible:

$\ mathbf {R} _T = \ mathbf {R} _R = \ begin {bmatrix} 1 & 0.4 \\ 0.4 & 1 \ end {bmatrix}$

3) Modèle de Kronecker avec une corrélation relativement forte:

$\ mathbf {R} _T = \ mathbf {R} _R = \ begin {bmatrix} 1 & 0.6 \\ 0.6 & 1 \ end {bmatrix}$

Nous utiliserons Python 3.4 dans cette partie. La fonction de calcul de la bande passante sera tirée d' une de mes publications précédentes .

 import numpy as np from numpy import linalg as LA import matplotlib.pyplot as plt from scipy.linalg import fractional_matrix_power def openloop_capacity(H_chan, SNR_dB): SNR = 10**(SNR_dB/10) Mt = np.shape(H_chan)[1] H_sq = np.dot(H_chan,np.matrix(H_chan, dtype=complex).H) lambdas = LA.eigvals(H_sq) lambdas = np.sort(lambdas)[::-1] c = 0 for eig in lambdas: c = c + np.log2(1 + SNR*eig/Mt) return np.real(c)

Définissez les principaux paramètres du système:

 Mr = 2 # number of receive antennas Mt = 2 # number of transmit antennas Rr1 = np.array([[1., .4], [.4, 1.]]) # case 1 Rr2 = np.array([[1., .6], [.6, 1.]]) # case 2 Rt1 = np.array([[1., .4], [.4, 1.]]) # case 1 Rt2 = np.array([[1., .6], [.6, 1.]]) # case 2 Rr1_half = fractional_matrix_power(Rr1, 0.5) Rr2_half = fractional_matrix_power(Rr2, 0.5) Rt1_half = fractional_matrix_power(Rt1, 0.5) Rt1_half_H = np.conj(Rt1_half).T Rt2_half = fractional_matrix_power(Rt2, 0.5) Rt2_half_H = np.conj(Rt2_half).T

Nous commençons la simulation:

 counter = 1000 SNR_dBs = [i for i in range(1, 21)] C_MIMO_uncorr = np.empty((len(SNR_dBs), counter)) C_MIMO_kron1 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron2 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron3 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron4 = np.empty((len(SNR_dBs), counter)) for c in range(counter): H_uncorr = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2) H_kron1 = np.dot(Rr1_half, np.dot(H_uncorr, Rt1_half_H)) H_kron2 = np.dot(Rr2_half, np.dot(H_uncorr, Rt2_half_H)) for idx, SNR_dB in enumerate(SNR_dBs): C_MIMO_uncorr[idx, c] = openloop_capacity(H_uncorr, SNR_dB) C_MIMO_kron1[idx, c] = openloop_capacity(H_kron1, SNR_dB) C_MIMO_kron2[idx, c] = openloop_capacity(H_kron2, SNR_dB) C_MIMO_uncorr_erg = np.mean(C_MIMO_uncorr, axis=1) C_MIMO_kron1_erg = np.mean(C_MIMO_kron1, axis=1) C_MIMO_kron2_erg = np.mean(C_MIMO_kron2, axis=1)

Dessin

 plt.figure(figsize=(7, 5), dpi=100) plt.plot(SNR_dBs, C_MIMO_uncorr_erg,'g-o', label='Uncorrelated') plt.plot(SNR_dBs, C_MIMO_kron1_erg, 'm-o', label='Kronecker model, case 1') plt.plot(SNR_dBs, C_MIMO_kron2_erg, 'r-o', label='Kronecker model, case 2') plt.title("Rayleigh flat fading (MIMO 2x2)") plt.xlabel('SNR (dB)') plt.ylabel('Ergodic capacity (bps/Hz)') plt.legend() plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()

Nous obtenons:

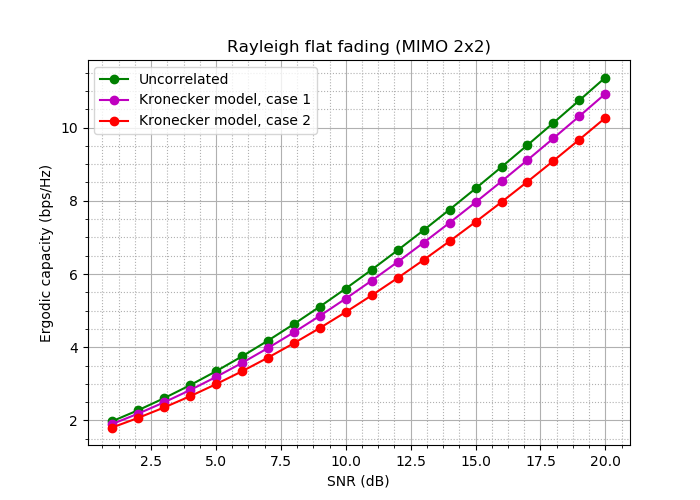
Fig. 18. Courbes de largeur de bande pour ces expériences.

Eh bien: la différence, bien que non critique, est!

Postface

Peut-être que l'un des lecteurs a peut-être remarqué que presque tout ce que nous avons examiné aujourd'hui (en détail et en passant) est assez bon sur les paramètres de l'objet matlab comm.MIMOChannel . Ce fait me semble très important:

premièrement, il systématise en outre ce qui est décrit ci-dessus,
et, deuxièmement, il souligne que nous nous attaquons aux problèmes actuels.

Eh bien, et maintenant, si vous utilisez de tels blocs, j'espère que ce sera plus clair pourquoi et quels stylos vous devez tordre.

Merci à tous pour votre attention!

J'ajouterai ici un lien vers les diapositives sur le sujet de Reiner S. Thomä (Ilmenau), sur lesquelles il nous a donné des conférences à l'époque. Je pense que quelqu'un sera utile!

Littérature

Paulraj, Arogyaswami, Rohit Nabar et Dhananjay Gore. Introduction aux communications sans fil spatio-temporelles. Cambridge University Press, 2003.
Goldsmith A. Communications sans fil. - Cambridge University Press, 2005.
Fontæn, Fernando Pærez et Perfecto Mariæo Espiæeira. Modélisation du canal de propagation sans fil: une approche de simulation avec Matlab. Vol. 5. John Wiley & Sons, 2008.
Farrokhi, Farrokh R. et al. "Efficacité spectrale des systèmes sans fil FDMA / TDMA avec réseaux d'antennes d'émission et de réception." Transactions IEEE sur les communications sans fil 1.4 (2002): 591-599.

Presque le canal MIMO le plus simple avec décoloration (modèle Kronecker inclus)