Fractales en nombre irrationnel. 2e partie

Partie 0: fractales en nombres premiers.
Partie 1: fractales en nombre irrationnel.



L'article contient des images Gif et contrastées. Les épileptiques peuvent avoir une crise d'épilepsie.

Dans un article précédent, nous avons examiné un algorithme de visualisation de séquence binaire. Souvenons-nous.

Prenez la séquence binaire. À titre d'exemple, les premiers bits d'une séquence fractale discutés dans un article précédent:

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

0100110110010011001001101100

Nous dessinons un champ de cellules carrées. Nous définissons les bits à la limite supérieure. La distance entre les bits est de deux cellules:



Pour chaque bit, tracez un tracé en pointillés le long de la diagonale (à travers la cellule). Pour les zéros, tracez le premier trait vers la droite:



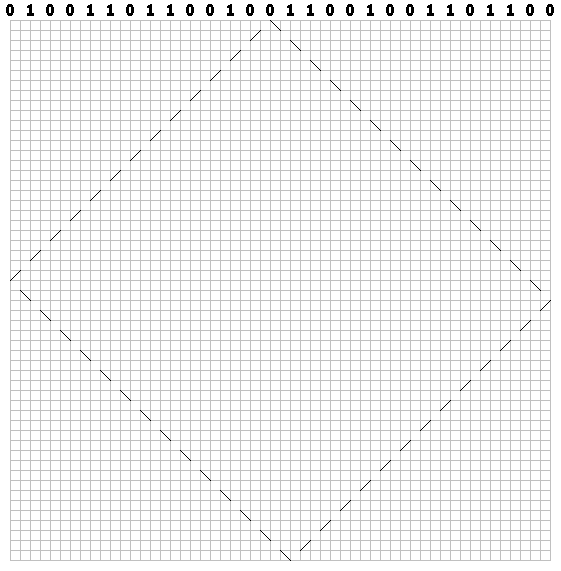
Pour les unités - à gauche:



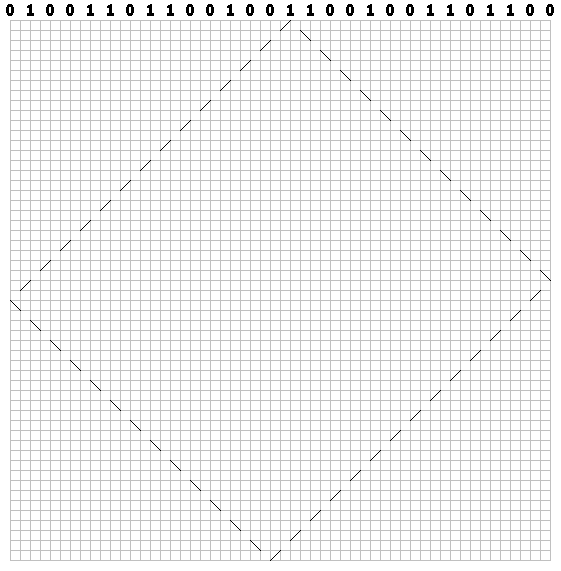
Tracez une trajectoire pour chaque bit. Nous avons obtenu un modèle de «billard»:



Un motif identique (sans défaut diagonal - la séquence est infinie, nous l'avons visualisée comme une séquence finale) peut être obtenu d'une autre manière. Inversez chaque bit pair de la séquence:

0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0 0 1 1 1 0 0 1

Ensuite, pour chaque bit, tracez des lignes pointillées verticales:



Nous mettons les bits sur la gauche, dessinons des lignes horizontales:



Nous combinons:



Après avoir écrit le premier article, deux questions sont restées sans réponse:

1. Est-il possible de dessiner un modèle fractal pour des nombres irrationnels. Tu peux. Le problème a été résolu dans un article précédent. Dans l'image ci-dessus - une partie du motif fractal pour $$$\ sqrt {2}$. Si vous sélectionnez l'une des courbes de ce modèle:



Obtenez la courbe fractale bien connue - «Fibonacci mot fractal».

2. La deuxième question est de savoir s'il est possible d'écrire un algorithme qui peint un motif:



Le deuxième problème sera abordé dans cet article. Nous colorerons les motifs à l'aide d'un métier à tisser, dont nous simulerons le travail à l'aide de JavaScript.



Dans le diagramme ci-dessus - la machine la plus simple. Il se compose de deux cadres à travers lesquels les fils sont étirés. Les cadres sont connectés aux pédales. Lorsque vous appuyez sur l'une des pédales, l'un des cadres monte. Les fils tirés à travers ce cadre montent et un fil transversal est étiré dans l'espace résultant entre les fils. Si vous étirez les fils pairs et impairs à travers différents cadres, vous obtenez un tissage en damier:



Dans les machines plus complexes, quatre cadres ou plus sont utilisés:


Métier à tisser Ashford à 4 puits

Afin de ne pas confondre quelle pédale appuyer, ils font un diagramme.



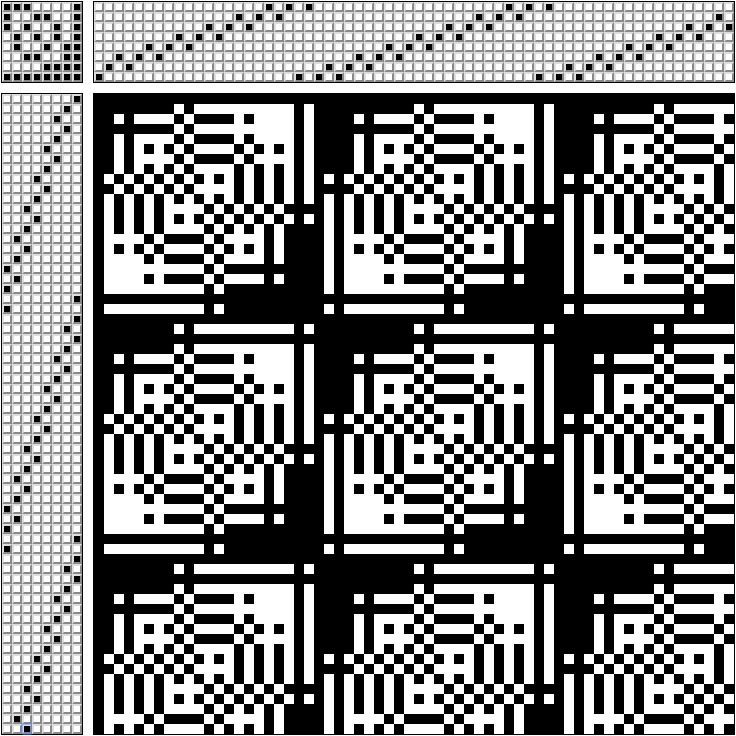
Dans la partie supérieure droite du motif, il est indiqué à travers quels cadres les fils passent (modèle pour un métier à 8 cadres).

Dans le coin supérieur gauche - quelles pédales serrer en même temps (chaque pédale est connectée uniquement avec son propre cadre).

Dans la partie inférieure gauche - dans quel ordre pédaler.

Dans la partie inférieure droite - quel tissage nous obtenons. Si vous étirez le fil blanc à travers le noir - nous obtenons un motif monochrome.

«Entrer» immédiatement le principe peut sembler un peu difficile. L'image ci-dessous montre comment le motif de tissage est formé:



Écrivons un script. Nous allons étirer les threads à travers les cadres en utilisant le tableau matriciel unidimensionnel2. Dans le tableau matriciel unidimensionnel1, nous écrivons la séquence de serrage des pédales. Dans array3 (tableau binaire 8x8), nous écrivons les pédales à bloquer en même temps.

for(var i=0;i<length;i++){ for(var j=0;j<length;j++){ if(array3[array1[i]][array2[j]]){ context.fillRect(i, j, 1, 1); } } } 

Script (fonctionne dans Google Chrome).

Avec l'aide de notre métier à tisser improvisé, nous pouvons dessiner une grande variété de motifs:



Mais historiquement, la personne moyenne n'a pas plus de deux jambes. Par conséquent, il est commode de serrer simultanément pas plus de deux pédales. L'un des modèles les plus populaires pour un métier à tisser est le suivant:



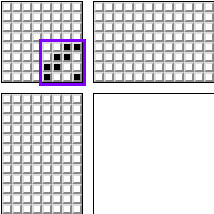
Pour 4 images. Et sa modification pour 8 images:



De façon inattendue, les modèles (ou un fragment de modèles) créés à l'aide de ce modèle sont similaires à nos modèles de «billard». De plus, ces motifs sont ombrés:



Vous pouvez apprendre à sélectionner des modèles de «billard» pour un métier à tisser. Un exemple:



Au début de l'article, nous avons déjà vu un fragment de ce modèle.

Terminez avec des métiers à tisser et écrivez un script pour visualiser les séquences binaires. Nous pouvons nous débarrasser de l'un des tableaux - le motif est diagonal symétrique. Comment remplir le tableau restant? Élémentaire:



Nous prenons la séquence pour $$$\ sqrt {2}$. Créez un tableau. Dans l'élément zéro du tableau, écrivez le bit zéro de la séquence. Prenez alternativement chaque bit de la séquence. Si le nième bit = 1 - écrivez dans le tableau a [n] = a [n-1] +1. Si bit = 0 - écrire a [n] = a [n-1] -1

$$

$$Q_n = \ lfloor n \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ... \\ a_n = \ begin {cases} a_ {n-1} +1, Q_n = 1; \\ a_ {n-1} -1, Q_n = 0 \ end { cas}$$

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } 

Nous vérifions:

  for(var i=0;i<size;i++){ context.fillRect(i, a[i]+50, 1, 1); } 

En fait, nous avons déjà reçu une fractale élémentaire, mais nous allons continuer.

Ensuite, nous traiterons de la matrice:



Résumer $$$x$et $$$y$. Divisez modulo par 4. Si le résultat résultant = 0 ou 1 - écrivez dans la matrice vrai. Pour 2 et 3, écrivez faux. On peut se passer d'une matrice (on ne sait pas à l'avance quelles valeurs maximales et minimales un [n] prend). Résumez un [x] et un [y]. Au montant résultant, ajoutez un certain nombre $$$C$(pour se débarrasser de ces cas lorsque le montant est un nombre négatif). Divisez le modulo par 4. Pour les valeurs 0 et 1, peignez le pixel avec les coordonnées $$$x$et $$$y$.

L'algorithme final ne prend que quelques lignes:

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } for(var x=0;x<size;x++){ for(var y=0;y<size;y++){ q=(a[x]+a[y]+512)%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); } } 

Visualisez nos séquences fractales.

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Vous pouvez facilement modifier le script afin d'obtenir une image RVB:

  q=(a[x]+a[y]+512)%4; /*if(q==0 || q==1) context.fillRect(x, y, 1, 1);*/ if(q==0) context.fillStyle = 'rgb(255,0,0)'; if(q==1) context.fillStyle = 'rgb(0,255,0)'; if(q==2) context.fillStyle = 'rgb(0,0,255)'; if(q==3) context.fillStyle = 'rgb(0,0,0)'; context.fillRect(x, y, 1, 1); 

Ci-dessus, nous avons ajouté un nombre à la somme a [x] + a [y] $$$C$. Si vous n'ajoutez pas ce nombre, la valeur minimale de la somme = -8, le maximum = 8 (pour $$$x$et $$$y$de 0 à 750). Si vous supprimez $$$C$- dans certains cas, la somme s'avère négative et non un multiple du 4e et pour ces cas le pixel n'est pas repeint (reste noir):

  q=(a[x]+a[y])%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); 

Vous pouvez l'imaginer comme si une partie de la fractale est en dessous d'une frontière imaginaire (en dessous de cette frontière, seules les valeurs négatives sont des multiples de 4: -4, -8, -12, ...).

Nous pouvons voir où se trouve cette frontière:

  if(a[x]+a[y]>=0) context.fillRect(x, y, 1, 1); 

Au lieu de diviser le modulo, nous pouvons comparer la somme avec une certaine valeur spécifique et ainsi peindre sur une seule «couche» de la fractale. À titre d'exemple, prenez la moyenne entre les valeurs minimale et maximale:

  q=(a[x]+a[y]); if(q==0) context.fillRect(x, y, 1, 1); 

En changeant les valeurs du minimum au maximum, nous pouvons voir comment les "couches" dans la dynamique changent:




De plus, nous pouvons «sur le front» comparer un [x] avec un [y] et également obtenir un motif fractal:

 if(a[x]==a[y]) context.fillRect(x, y, 1, 1); 

La séquence suivante:

$$

$$Q_n = \ lfloor n (\ sqrt {2} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fractale:



RVB:



Couche intermédiaire:



En dynamique:

$$

$$Q_n = \ lfloor n \ sqrt {3} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fractale:



RVB:



Couche intermédiaire:



En dynamique:

$$

$$Q_n = \ lfloor n (\ sqrt {3} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fractale:



RVB:



Couche intermédiaire:



En dynamique:

$$

$$Q_n = \ lfloor n \ sqrt {5} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

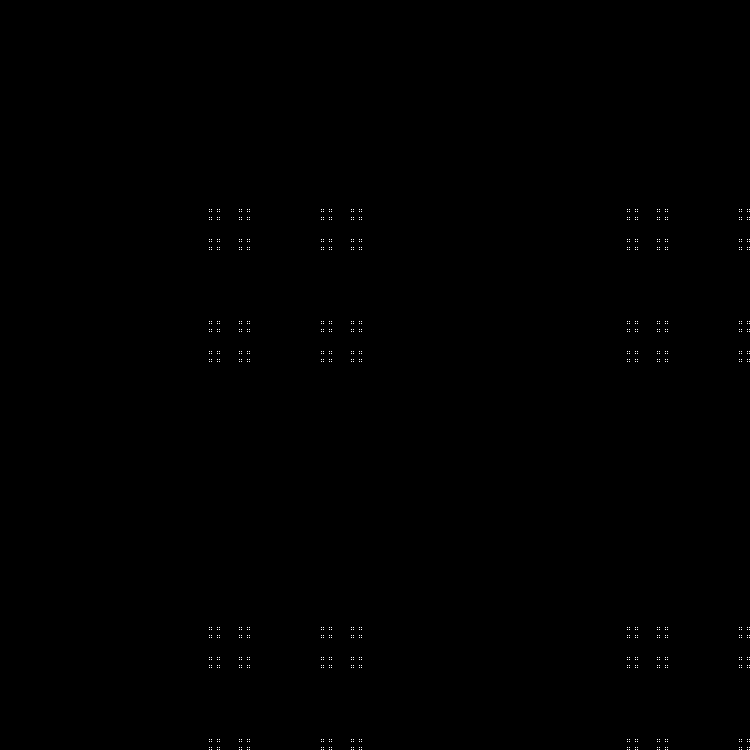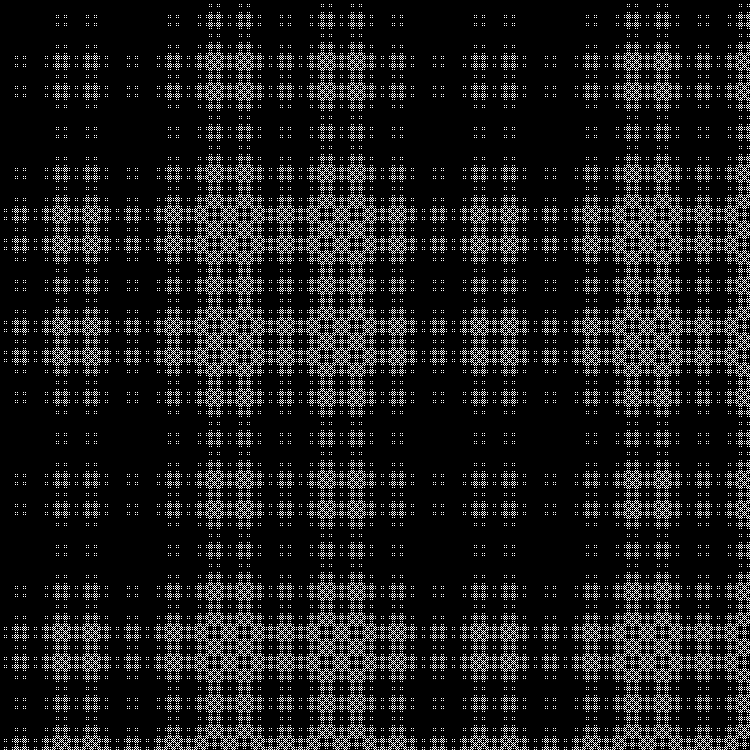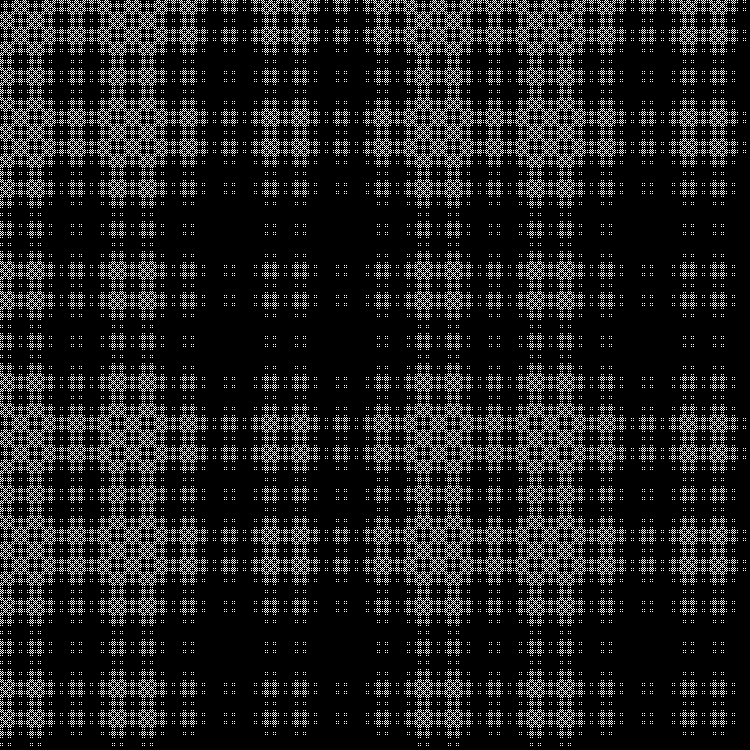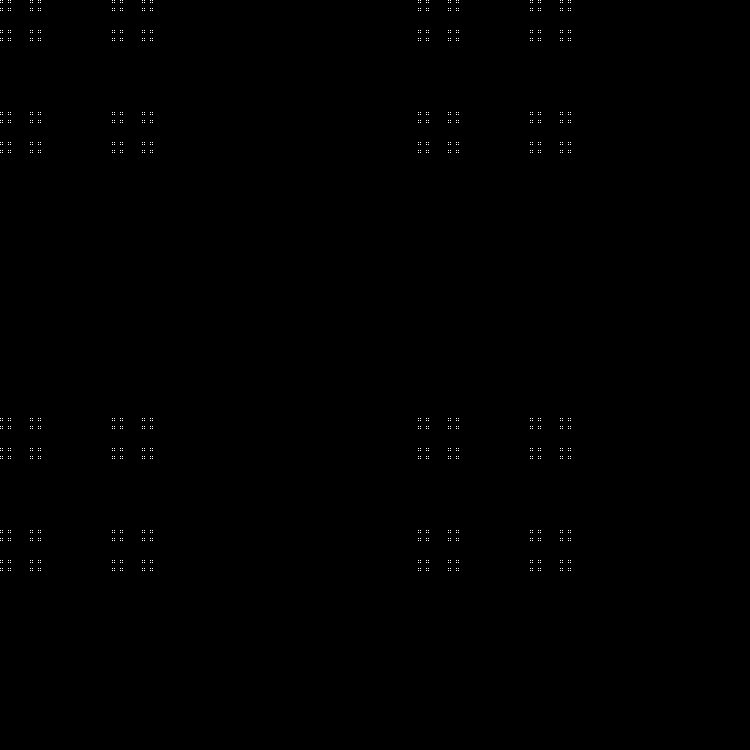
Fractale:



RVB:



Couche intermédiaire:



En dynamique:



Eh bien, notre fractale préférée (une partie de ce motif peut être dessinée à l'aide de billards, avec des tailles de côtés égales aux nombres de Fibonacci):

$$

$$Q_n = \ lfloor n (\ sqrt {5} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fractale:



RVB:



Couche intermédiaire:



En dynamique:



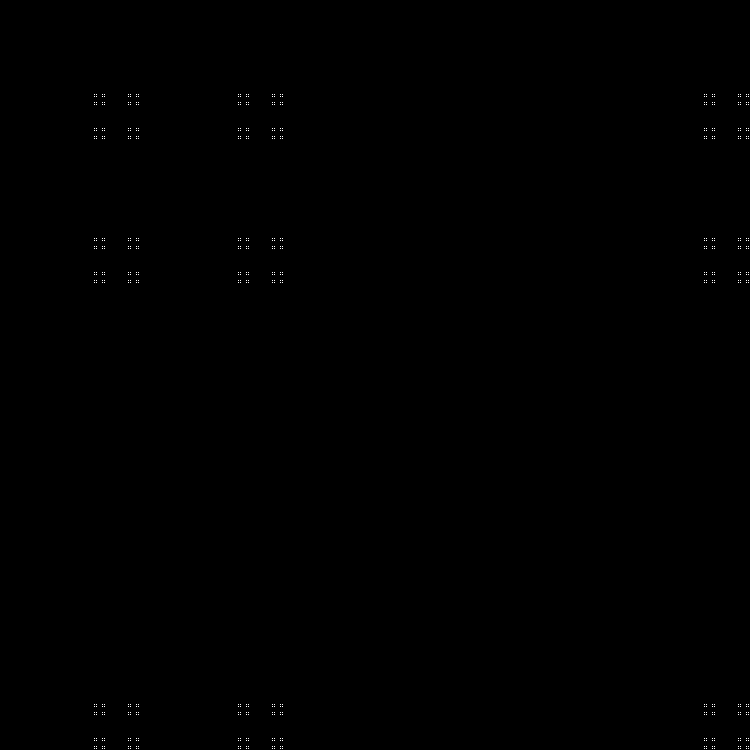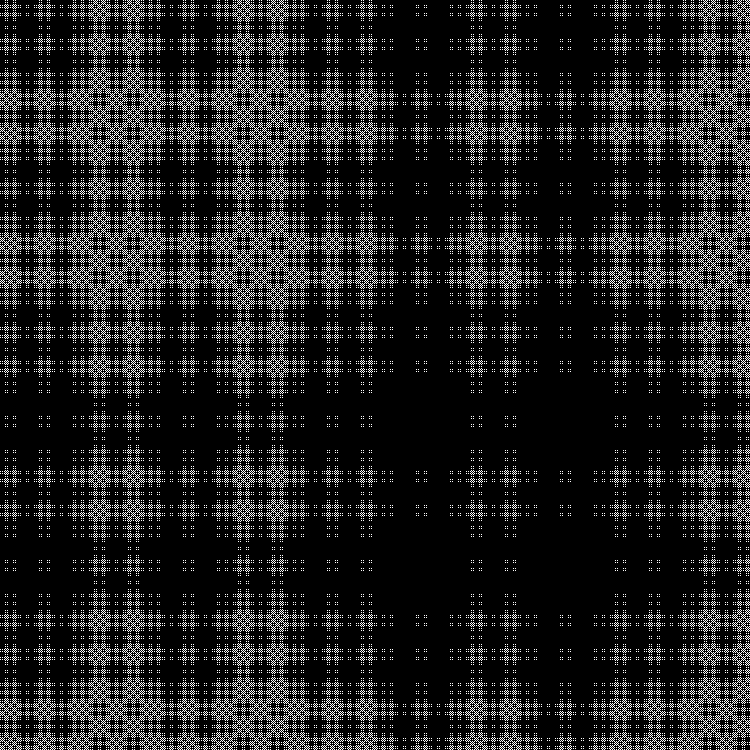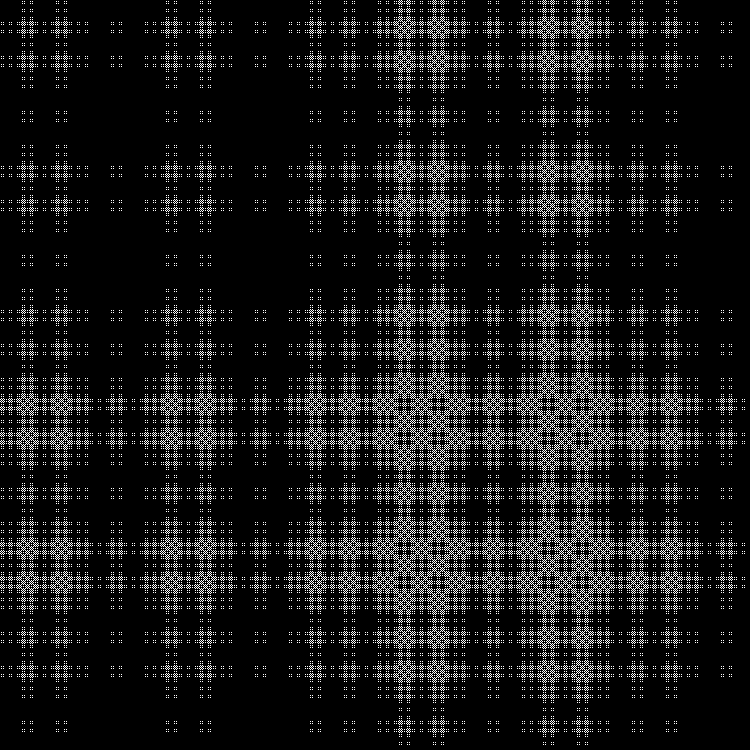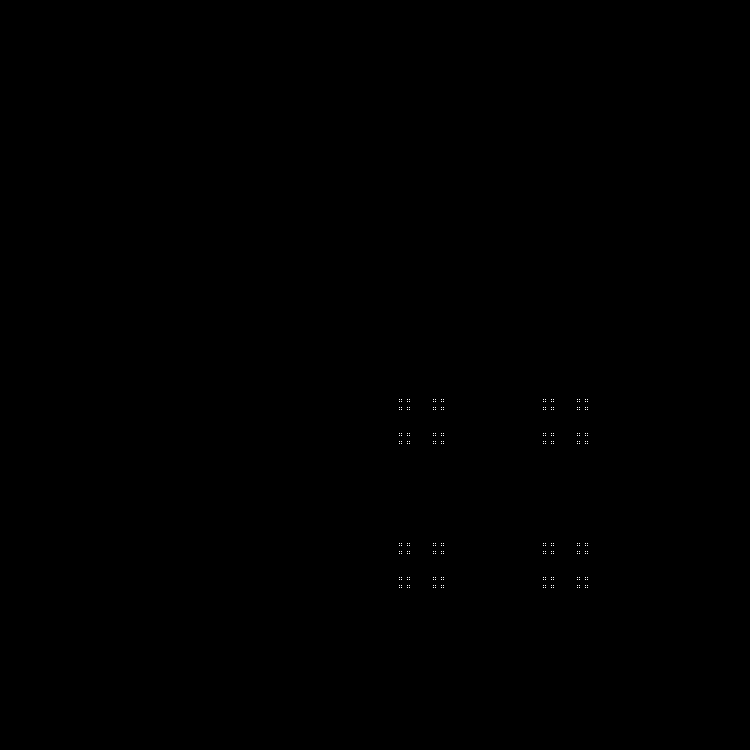
Une autre séquence à compléter:

$$

$$Q_n = \ lfloor n ^ {2} \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Motif:



RVB:



Couche intermédiaire:



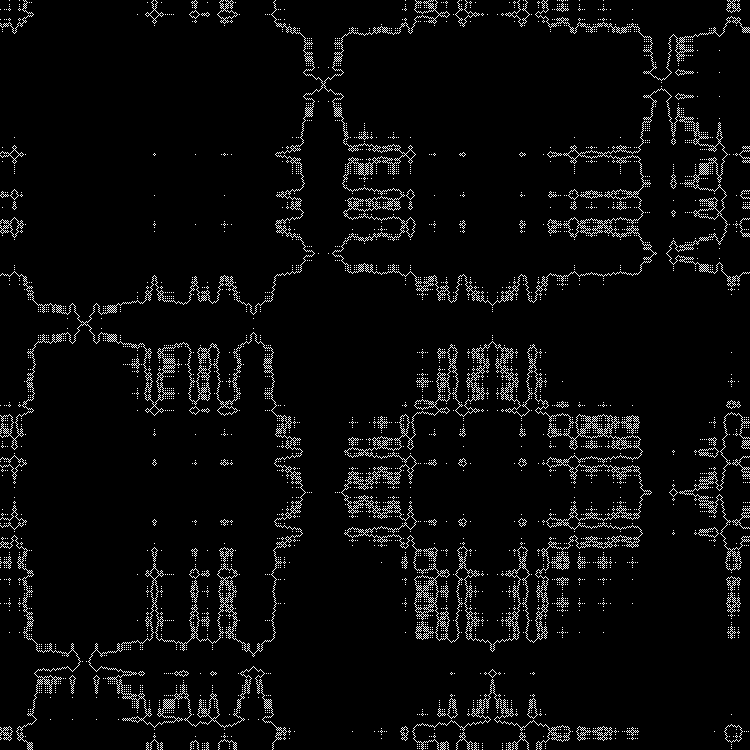
En dynamique:



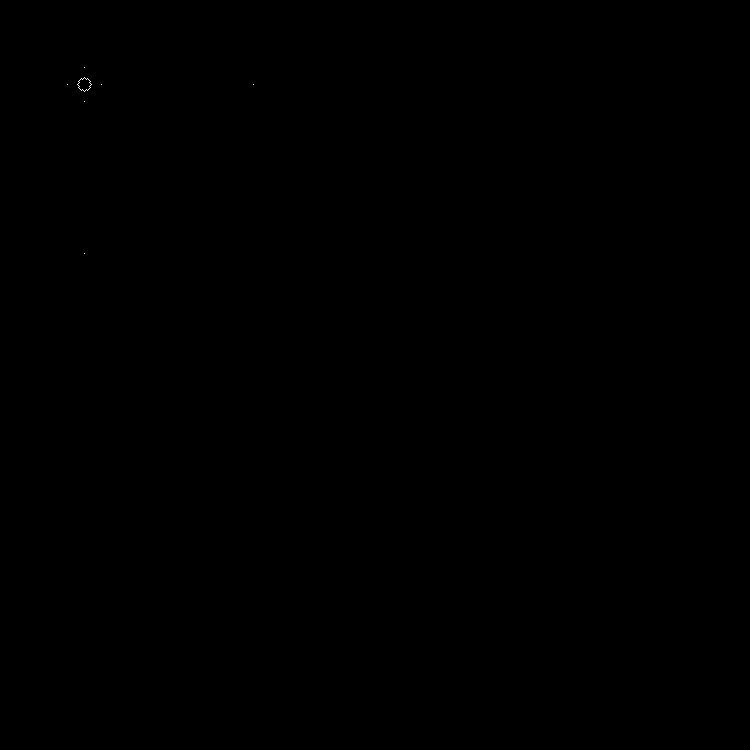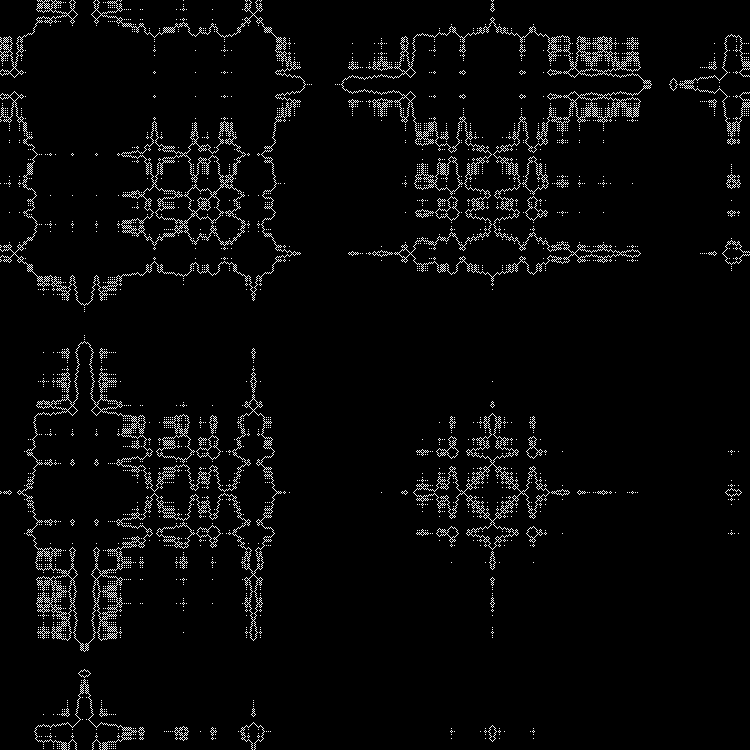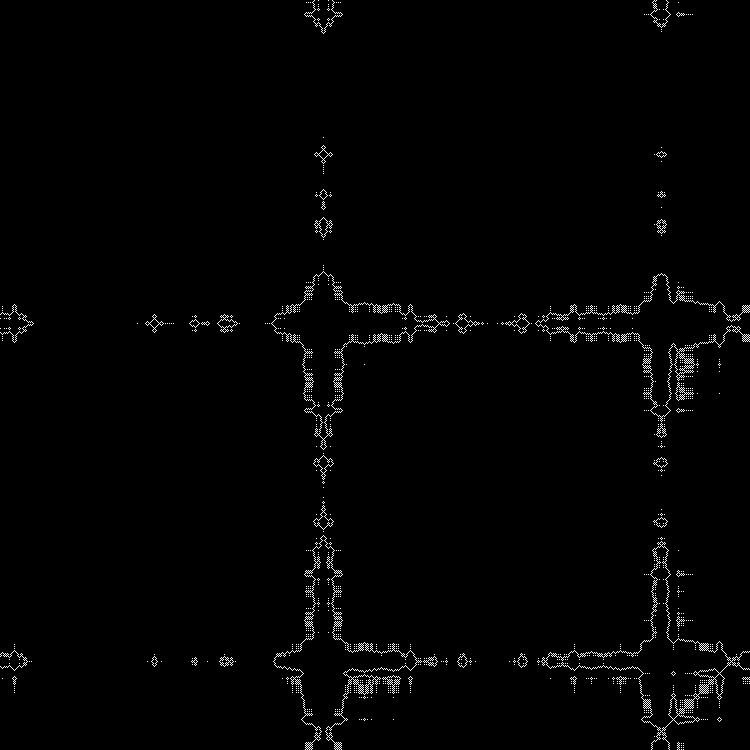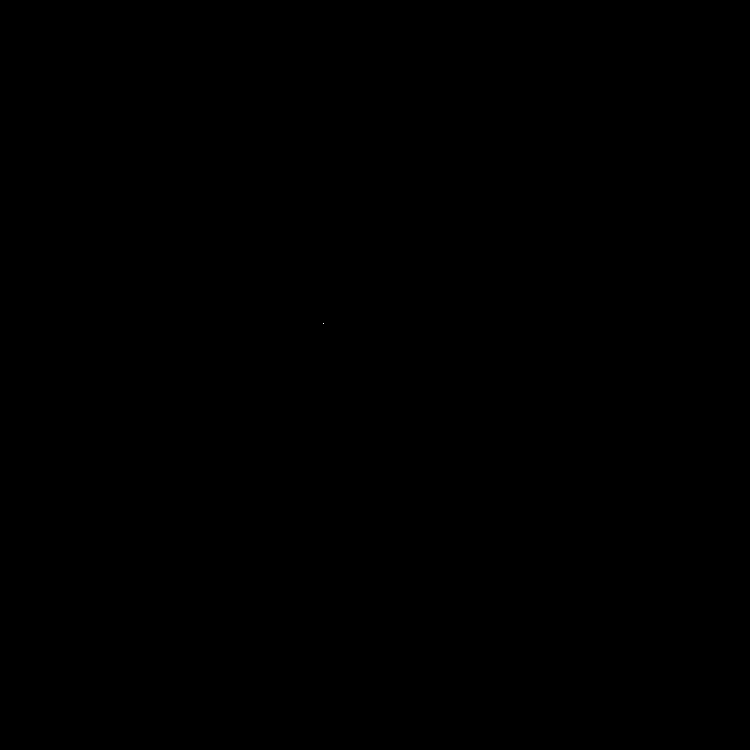
D'autres racines carrées peuvent être introduites dans le script . (Vous pouvez conduire en valeurs fractionnaires).

Dans le deuxième script, vous pouvez piloter la séquence manuellement.

Un autre script pour le billard. Coordonnées de la souris - dimensions du billard. Le motif de gauche est formé de la séquence obtenue en utilisant le reste de la division (détails dans l'article précédent). Du côté droit - parité $$$\ lfloor n \ frac {y} {x} \ rfloor$.