Présentation

À propos du projet

Le projet «Taux de change absolu» est engagé dans l'analyse des taux de change appariés, la répartition des taux de change absolus à partir d'eux et leur analyse. Dans le cadre du projet, une méthodologie de conversion des taux de paire en taux de change absolus a été obtenue. Pour cela, l'ABS en devise absolue est défini. Toutes les devises disponibles sont exprimées en termes d'ABS.

Une description détaillée de la technologie est donnée dans l'article «Des paires de devises aux taux de change absolus» .

À propos du problème

Cet article aborde le problème d'une analyse qualitative de la cohérence des taux de change.
La nécessité d'étudier la relation entre les devises est due aux exigences de sélection des instruments financiers dans le portefeuille d'investissement et à la capacité de prédire le comportement des devises sur la base de données sur d'autres devises qui leur sont associées.

Il est conseillé d'inclure des instruments à forte connectivité multidirectionnelle dans le portefeuille d'investissement. Cela vous permet de réduire le risque global du portefeuille.

Et, si vous trouvez des outils avec un haut degré de connectivité, alors en fonction du comportement de certains, vous pouvez prédire le comportement des autres.

À propos de l'expérience

Sélection de la méthode

Comme données initiales de l'expérience, il existe des séries de données avec des taux de change absolus (voir fichier source. Feuille «Taux de change absolus» ).



Pour étudier la connectivité d'une série de données numériques, il est préférable d'utiliser la corrélation de Pearson (voir Corrélation - Wikipedia ).

Le coefficient de corrélation a une plage de valeurs de «-1» à «+1». De grandes valeurs négatives indiquent une forte relation multidirectionnelle. De grandes valeurs positives indiquent une forte connectivité unidirectionnelle. La proximité du coefficient à «0» indique l'absence de communication.

Que voulez-vous obtenir?

Le but de l'expérience est d'obtenir des groupes de devises avec un haut degré de connectivité. De plus, le signe de la communication est également intéressant.

Lieu

Tous les calculs seront effectués dans le système Wolfram Mathematica (voir Wolfram Mathematica - Wikipedia ). Et nous utiliserons les ressources cloud gratuites de Wolfram.Cloud .

La ressource spécifiée vous permet de créer des cahiers en ligne avec des calculs et vous permet de fournir un accès pour une visualisation générale. Le cahier de cette expérience se trouve ici .

Plan

Nous effectuerons des calculs selon le plan suivant.

Tout d'abord, nous calculons la matrice de corrélation. Les colonnes et les lignes de la matrice correspondront aux différentes devises. À l'intersection de la colonne et de la ligne se trouve le coefficient de corrélation des paires.

Ensuite, nous sélectionnons des paires de devises avec les liens les plus forts. Placez les paires sélectionnées sur le graphique (voir Graphique (mathématiques) - Wikipedia ).

Les nœuds du graphique sont des devises. Les bords du graphique indiqueront la relation entre les devises. La couleur de la côte indiquera le signe de liaison. Le vert indique une relation positive et le rouge indique une relation négative.

La séquence de calculs indiquée sera effectuée à la fois pour les cours absolus et pour leurs modifications. Une analyse de la relation des cours absolus vous permet d'explorer des processus lents (plus d'une journée). Une analyse de la relation entre les variations des taux de change absolus nous permettra d'étudier les connexions rapides entre devises (un jour).

Résultats

Profondeur d'échantillonnage

Le fichier source contient les données des 150 derniers jours. Selon eux, le calcul sera effectué.

Nuage de devises

L'expérience a impliqué 45 devises.



Une liste complète des devises peut être consultée sur la feuille «Résumé des devises» du fichier source .

Corrélation de taux absolue

Ci-dessus (voir. Plan), il était prévu de calculer la matrice de corrélation des taux absolus. Le résultat est montré dans l'image ci-dessous.



Ici, le rouge correspond à une connexion positive et le bleu à une connexion négative. Pour la compréhension, une échelle de gradation est donnée. En dessous et à gauche se trouvent les tickers de devises (noms courts).

Graphique de dépendance de taux absolu

La matrice de corrélation a permis de distinguer deux groupes de devises à fort degré de connectivité. Pour ce faire, des paires avec une corrélation supérieure à 0,9 ont été sélectionnées et transférées sur le graphique.



Le premier groupe a rassemblé des devises fortement tributaires du dollar américain. Voici les devises de quatre pays arabes faisant du commerce de pétrole, le dollar de Hong Kong et le dollar américain lui-même. Toutes les dépendances sont positives (unidirectionnelles).

Le deuxième groupe a rassemblé les devises européennes. Au centre se trouve l'euro lui-même et autour de lui les monnaies de la Pologne, de la Roumanie et du Danemark. Toutes les dépendances sont positives (unidirectionnelles).

Variations relatives des taux absolus

Pour de plus amples recherches, nous avons calculé la série de changements relatifs des taux absolus. La formule pour les calculs est la suivante.



La différence entre les valeurs successives sera corrélée à la première des deux. Ainsi, nous recevrons une variation relative du taux absolu.

Corrélation des variations relatives des taux absolus

Comme pour les cours absolus, nous obtenons une matrice de corrélation pour les mesures relatives des cours absolus. Nous donnons un affichage graphique de la matrice.



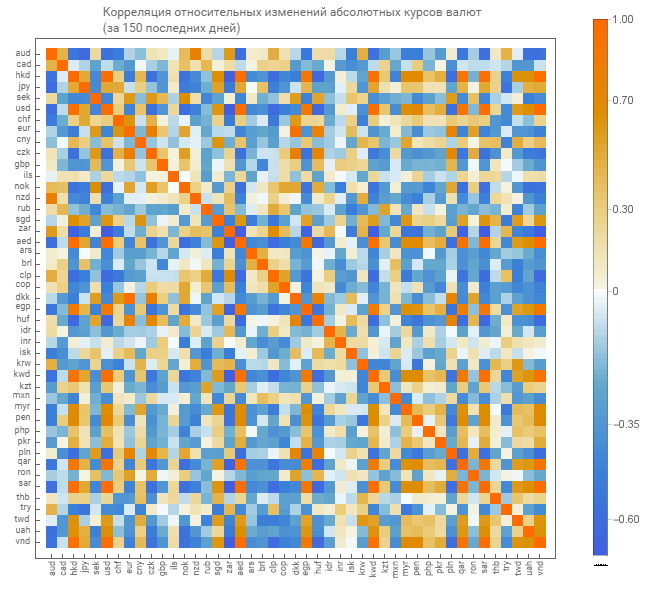
Il existe déjà une matrice de tons plus clairs. Ce qui indique un moindre degré de connectivité.

Graphique de dépendance des variations relatives des taux absolus

Dans la matrice de corrélation des changements relatifs, nous sélectionnons des paires de devises avec un haut degré de connectivité. Seul le niveau d'échantillonnage ici est déjà de 0,6 (ici et au-dessus, ce coefficient a été choisi en tenant compte d'un petit nombre de paires pour la sortie sur le graphique).



Dans le cas de changements relatifs reçus 3 groupes de devises. Le groupe supérieur combinait les devises de l'Australie et de la Nouvelle-Zélande. Le groupe inférieur regroupait les devises européennes. Le groupe intermédiaire autour du dollar de Hong Kong combinait les devises des États-Unis, du Vietnam, de cinq pays arabes - exportateurs de pétrole, d'Afrique du Sud et du Pérou.

De plus, la forte dépendance négative à l'égard du rand sud-africain présente une caractéristique intéressante.

Conclusions

À la suite de l'expérience, nous avons réussi à obtenir ce qui suit.

Placer les données de la matrice de corrélation dans un graphique mathématique est une bonne pratique de visualisation pour la matrice de corrélation. Une application plus poussée de cette méthode simplifiera la compréhension des relations dans le groupe de séries de nombres.

Une méthode formelle de regroupement des marchés monétaires est trouvée. Il a été possible de distinguer formellement les marchés de l'Europe, de l'Amérique avec l'Asie et l'Océanie. Cette méthode peut considérablement raccourcir la voie pour révéler les influences mutuelles entre les marchés de différents pays et devenir un bon outil pour un analyste financier.

L'inclusion du rand sud-africain dans le portefeuille d'investissement avec le dollar américain réduira les risques d'un tel portefeuille.

Catalogue d'articles