Compte tenu: 12 pièces, dont l'une est fausse, elle ne diffère que par son poids. Inconnu plus léger ou plus lourd. Des échelles à effet de levier sont données qui montrent que la charge d'un côté est plus lourde. Pour 3 pesées, vous devez trouver une fausse pièce.
Par expérience, je vous conseille de ne pas vous précipiter, de décider par écrit. Le puzzle «12 pièces, 3 pesées» a surgi plusieurs fois dans ma vie. La première fois que mon amie me l'a demandé, elle a décidé après les Jeux olympiques et j'ai dû me casser la tête pendant quelques heures. Et quelques années plus tard, cela ne m'a pas été donné immédiatement. Si vous voulez décider par vous-même - faites-le sur un morceau de papier.
Vous trouverez ci-dessous une analyse et les étapes de la solution. Les étapes seront réalisées selon une méthodologie universelle de résolution de problèmes, applicable à la fois à la programmation et à la vie. Avec l'approche, résoudre le puzzle sera facile.
Je vous propose, avant de lire, de proposer une solution. Avez-vous une réponse? Vérifié?
S'il s'agissait d'un logiciel, les questions seraient: «Avez-vous programmé, testé l'algorithme? Avez-vous examiné les cas de test et les avez-vous vérifiés? »
Comme l'expérience le montre, pour le résoudre, il est nécessaire de dessiner un arbre de décision et de vérifier les 12 cas.

1. AstucesDans le processus de résolution, cela aidera:1) Diminution de l'entropie (mesures de l'incertitude) et réponses aux questions:
- Qu'avez-vous appris à l'étape précédente?
- Qu'est-ce qui réduit l'incertitude?
- De quelles informations disposons-nous?
- Que devez-vous savoir d'autre?
Les questions conviennent à n'importe quelle tâche, projet. Les réponses à ces questions aident à réduire le risque de non-respect des délais, les dépassements de budget et le rattrapage des supérieurs.
2) Décomposition. L'approche du simple au complexe. Si vous préparez une solution aux cas les plus simples, puis utilisez-les pour résoudre le problème (diviser et conquérir l'algorithme), ce sera plus facile que de représenter la situation dans votre tête.
Les algorithmes de division et de conquête décomposent une tâche en deux sous-tâches ou plus du même type, mais plus petites en tâches élémentaires, et combinent leurs solutions pour obtenir une réponse au problème d'origine.Composez des questions pour la décomposition. Que suggéreriez-vous?
2. DécompositionQuelles questions avez-vous formulées pour la décomposition? Des matchs?
1) Quelle est la situation la plus élémentaire? Que pouvons-nous faire en une seule pesée?
Pour une pesée, nous pouvons déterminer quelle pièce est la plus lourde, si le poids des pièces est égal.
2) Si nous avons 2 pièces et, comme vous le savez, le faux est plus dur ou plus léger. Comment déterminer un faux en une seule pesée?
Il faut peser les pièces, et en fonction de la flèche de la balance, déterminer le faux.
3) Si nous avons 2 pièces et, on ne sait pas, la contrefaçon est plus difficile ou plus facile, comment déterminer la contrefaçon en une seule pesée?
Après avoir pesé l'une des 2 pièces présentées avec la troisième pièce, dont on sait qu'elle est authentique.
4) Si nous avons 3 pièces et, comme vous le savez, le faux est plus dur ou plus léger. Comment déterminer un faux en une seule pesée?
Il est nécessaire de comparer deux de ces pièces, si elles sont égales, la troisième pièce est fausse.
5) Si nous avons 3 pièces et, on ne sait pas, le faux est plus difficile ou plus facile. Est-il possible de déterminer un faux en une seule pesée?
Malheureusement non.
6) Si nous avons 4 pièces et que le faux inconnu est plus dur ou plus léger, pouvons-nous déterminer le faux en une seule pesée?
Malheureusement non.
7) Si nous avons 4 pièces et, on ne sait pas, le faux est plus dur ou plus léger, combien de pesées pouvez-vous déterminer comme faux?
Pour deux pesées.
Ensuite, à partir de cas élémentaires, nous collectons des situations de 8, 9, 10, 11 et 12 pièces. Comment voyez-vous la solution?
Voici la solution complète.
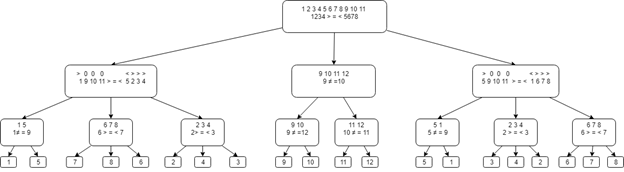
3. DécisionPremière étape: divisez les pièces en 3 groupes de 4: 1 2 3 4, 5 6 7 8, 9 10 11 12.
Comparez les deux premiers groupes. Trois options sont possibles:
- le premier groupe est plus lourd;
- le deuxième groupe est plus lourd;
- sont égaux.

1) Si les groupes sont égaux, la fausse pièce appartient au troisième groupe. Il faut trouver une fausse pièce de 4 pièces en deux pesées.
Divisez le troisième groupe en deux: 9 10 11 12
Comparez 9 et 10:
- s'ils sont égaux, alors la fausse pièce dans le deuxième groupe - comparer 9 et 11. Si 9 et 11 sont égaux, alors le faux - 12, sinon -11
- s'ils ne sont pas égaux, alors faux dans le premier groupe - comparer 10 et 12. Si 10 et 12 sont égaux - faux - 9, sinon - 10.
Nous avons donc trouvé une fausse pièce.
2) Considérons le deuxième cas. Si le premier groupe est plus lourd que le second, alors nous attribuons au premier groupe le signe ">", au deuxième groupe le signe "<", le troisième groupe - "0".
Nous divisons les pièces en groupes 1 9 10 11 et 5 2 3 4, pesés. Trois options sont possibles:
- Sont égaux. La pièce contrefaite est parmi les nombres: 6 7 8. Comparez 6 et 7, s'ils sont égaux, la contrefaçon est 8, si 6 est plus grand, la contrefaçon - 7, si 7 est plus grand, la contrefaçon - 6, puisque dans ce cas la pièce contrefaite est plus facile.
- Le premier groupe est plus lourd, puis la fausse pièce est 1 ou 5. Comparez 1 et 9 s'ils sont égaux - la fausse pièce - 5, sinon - 1.
- Le premier groupe est plus facile, puis faux entre les pièces 2 3 4, car on sait que 9, 10 et 11 sont réels, et le deuxième groupe ne peut être contrebalancé que par les pièces 2, 3 et 4. Comparez 2 et 3, s'ils sont égaux, faux 4, si 2 est plus lourd, alors faux est 2, sinon 3e est faux.
3) Le cas où le deuxième groupe est plus lourd que le premier est similaire au second.
Le diagramme général de l'arbre de décision est présenté ci-dessous.
ConclusionLorsqu'une tâche arrive pour révision ou débogage, il est bon d'appliquer l'approche ci-dessus:
- Décidez ce qui est donné?
- Quels cas / tâches élémentaires peuvent être décomposés?
- Qu'est-ce qui est inconnu pour résoudre le problème? Quelles expériences faut-il faire pour réduire l'entropie?
- Courez.
- Le problème est-il résolu? Non? Revenez à l'étape 1.
Solutions réussies.