Estimation de VaR et ConVaR pour le cours de bourse de la société kazakhe

Au cours des dernières décennies, l'économie mondiale tombe régulièrement dans ce tourbillon de crises financières qui ont touché chaque pays. Cela a presque conduit à l'effondrement du système financier existant, de ce fait, les experts en modélisation mathématique et économique ont tous recours à des méthodes pour contrôler les pertes de l'actif et du portefeuille dans le monde financier (Lechner, LA, et Ovaert, TC (2010). Il y a une tendance croissante à la modélisation mathématique d'un processus économique pour prédire le comportement du marché et une évaluation de sa durabilité (ibid). Ayant sans l'attention nécessaire pour contrôler et évaluer correctement les menaces, tout le monde comprend qu'il est capable de déclencher coût énorme dans le développement de l'organisation ou même faire faillite.

La Value at Risk (VaR) a finalement été une approche régulière pour attraper le risque parmi les institutions du secteur financier et son régulateur (Engle, R., et Manganelli S., 2004). Le modèle est initialement appliqué pour estimer la valeur de la perte dans le portefeuille de placements au cours d'une période de temps donnée et à une probabilité d'occurrence donnée. Outre le fait d'utiliser la VaR dans le secteur financier, il existe de nombreux exemples d'évaluation de la valeur à risque dans différents domaines tels que l'anticipation du personnel médical pour développer la gestion des ressources de santé Zinouri, N. (2016). Malgré sa primitivité appliquée dans une expérience réelle, le modèle comporte des inconvénients dans l'évaluation (ibid.).

L'objectif du rapport est une description du modèle de VaR existant, y compris l'une de ses versions de mise à niveau, à savoir, la valeur conditionnelle à risque (CVaR). Dans la section suivante et la section 3, l'algorithme d'évaluation et les tests du modèle sont expliqués. Pour une illustration éclatante, la perte attendue est estimée sur l'actif de l'une des sociétés kazakhes qui évolue sur le marché financier sur une longue période. Les dernières sections 4 et 5 discutent et démontrent les résultats des travaux de recherche.

Contexte

On pense que la première utilisation de la VaR par les organisations financières géantes il y a jusqu'à 40 ans et en conséquence la VaR est devenue populaire parmi d'autres sociétés de négoce, même les régulateurs financiers ont porté attention au modèle (Linsmeier, TJ, et Pearson, ND 2000). Par exemple, la Securities and Exchange Commission des États-Unis a inscrit la VaR sur une liste de méthodes quantitatives de calcul du risque de marché et des biens immobiliers en 1997 (ibid).

En fait, selon les articles de Lechner, LA et Ovaert, TC (2010) ainsi que de Linsmeier, TJ et Pearson, ND (2000), la VaR est une équation d'estimation exprimée en unités monétaires qui ne dépassent pas la perte d'amplitude. pendant une période donnée et un niveau de confiance donné. En règle générale, le niveau de confiance de l'estimation du modèle (99%, 97,5%, 95%) ou en d'autres termes la probabilité qu'un cas défavorable se soit produit et l'influence sur le marché sont égaux à 1, 2,5 et 5% (ibid).

L'équation bien connue de la VaR peut être décrite (Phelps S, 2018):

$$$(1) \ VaR (X) = \ min \ \ {x \ \ epsilon \ R: 1-F_x (-x) \ geq \ alpha \}$

Où X est une variable aléatoire qui effectue le montant de la valeur du portefeuille et est une fonction de distribution cumulative (ibid).

D'autre part, Hooper GP (1996, cité dans Lechner, LA, et Ovaert, TC 2010) dénote la VaR avec confiance alpha définit de manière assez élémentaire:

$$$(2) \ VaR ^ \ alpha (X) = \ sigma \ sqrt {\ delta t} N ^ {- 1} \ alpha$

O Where $$$\ sigma$est l'écart-type des rendements boursiers sélectionnés, $$$\ delta t$est la racine carrée de la période de temps fixe et $$$N ^ {- 1}$est la fonction de distribution cumulative (CDF) pour une distribution normale (Lechner, LA et Ovaert, TC 2010).

Bien que la VaR soit une méthode bien connue et gérée pour estimer le risque de portefeuille décidé, il existe des lacunes dans le cas où la mesure de la vulnérabilité aux problèmes ultimes du marché, à savoir, l'exemple est lié à la probabilité que des événements de marché extrêmes ne soient pas correctement pris dans la queue de la distribution normale (Capiński, MJ 2015). Pour résoudre ce problème, la valeur conditionnelle à risque (CVaR) a été créée qui tient compte de la valeur attendue de la perte au lieu de la VaR (ibid). CVaR définit comme:

$$$(3) \ CVaR ^ \ alpha (X) = \ frac {1} {\ alpha} \ int ^ \ alpha_0 VaR ^ \ beta (X) d \ beta = \ frac {-1} {\ alpha} q ^ \ beta (X) d \ beta$

$$$(4) \ CVaR ^ \ alpha (X) = - \ frac {1} {\ alpha} (E [X 1 _ {\ {X \ leq q ^ \ alpha (x) \}}] + q ^ \ alpha (X) (\ alpha-P [X \ leq q ^ \ alpha (X)]))$

Où Ahn D.-H. et.al (1999, cité dans Capiński, MJ 2015) interprètent $$$-q ^ \ alpha (X)$
en VaR de X variable aléatoire (retour d'un cours de bourse) avec probabilité $$$\ alpha$et définit comme le quantile supérieur de X.

De plus, Acerbi C. et Tasche D. (2002, cité dans Capiński, MJ 2015) confirment que «le CVaR est une mesure de risque cohérente». Rockafellar, RT et Uryasev, S. (2000) remarquent que CVaR a des caractéristiques supplémentaires: équivariantes aux transitions, positivement homogènes, convexes, etc.

Le chapitre suivant de l'article montre la mise en œuvre de la valeur à risque (VaR) et de la valeur conditionnelle à risque (CVaR) bien connues, également annoncées comme un déficit attendu (ES) constaté dans les travaux de Rockafellar, RT et Uryasev, S. (2000) en utilisant la technologie de l'information sur des données réelles.

Méthodologie

Examinons les méthodes de calcul de la VaR les plus couramment utilisées, ainsi que ses avantages et ses inconvénients.

Selon le rapport de Lechner, LA et Ovaert, TC (2010), la simulation historique est une approche répandue pour évaluer la VaR et sa modification. Dans la modélisation historique des données, nous prenons les valeurs des fluctuations financières du portefeuille qui sont déjà connues à partir des mesures passées. Ce n'est donc que la séquence logique que l'inconvénient de cette méthode est l'impossibilité de construire des prédictions pour les portefeuilles sans information à ce sujet. La méthode de Monte Carlo est à bien des égards identique à la méthode de modélisation historique, celle utilisée pour la technique de haute précision, la principale différence claire que le calcul de la simulation de Monte Carlo n'est pas basé sur des données réelles, mais réalisé sur des valeurs générées aléatoirement. L'avantage de cette méthode est la possibilité de considérer comme un grand nombre de situations, et d'émuler le comportement du marché dans des conditions extrêmes ainsi qu'il n'y a pas besoin d'une approximation entre les facteurs de risque et les changements dans un portefeuille (Glasserman, P., Heidelberger, P et Shahabuddin, P., 2002). L'inconvénient évident est les grandes ressources de calcul nécessaires pour mettre en œuvre cette approche (ibid).

Naturellement, ce ne sont pas les seules méthodes de calcul des modèles de VaR. De plus, il existe à la fois de simples modèles linéaires et quadratiques de prévision des prix et une méthode de variation assez compliquée, qui n'ont pas été abordés dans l'essai.

Analyse des données

En tant que données secondaires pour tester l'évaluation précise, le stock de minéraux KAZ est pris. Pour clarifier le travail, le prix de clôture ajusté est utilisé pour la simulation dans un modèle. Les actions de la société KAZ Minerals (KAZ.L) sont l'un des titres négociés avec succès parmi les entreprises kazakhes à la Bourse de Londres (LSE) et sont également classés dans la liste Premium Equity Commercial Companies (London Stock Exchange, 2019). L'entité se présente comme la société minière de cuivre massive au Kazakhstan (Kazminerals.com.2019).

Les données historiques du cours de l'action sont téléchargées à partir du site Web de Yahoo Finance (Finance.yahoo.com, 2019). Pour assurer la validité des travaux, la période d'un an du 22 mars 2018 au 22 mars 2019 est respectée. De plus, pour éviter la perturbation de l'information, dans l'analyse, les données historiques du cours de l'action KAZ.L sont téléchargées au format CSV (Comma-Separated Values) car le format CSV est compatible avec le programme Microsoft Excel (Excel) . Les données choisies du projet sont présentées sous forme de graphique linéaire à l'aide d'Excel dans la figure 1.

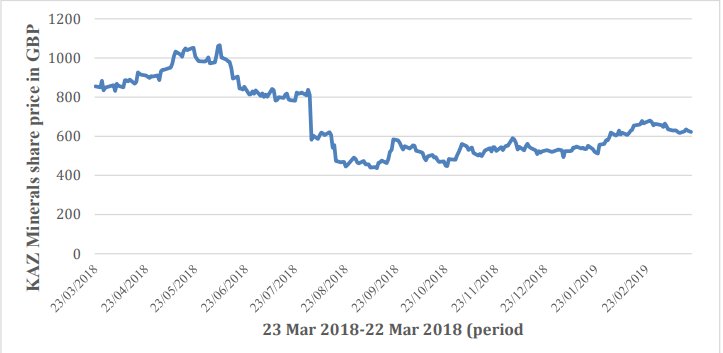
Figure 1. La dynamique du changement du cours de l'action KAZ Minerals pendant un an

En raison de la limitation de la chronologie du rapport, au lieu d'utiliser un langage de programmation comme Python pour la mise en œuvre de modèles d'évaluation, les données sont entièrement analysées dans Excel.

Constatations

Dans la section précédente, les modèles pour prévoir les pertes potentielles dans un portefeuille sur la base de l'équation VaR et CVaR et utilisé les variations du cours de l'action KAZ Minerals du 23 mars 2018 au 23 mars 2019, téléchargés à partir de la source Web officielle Yahoo Finance (Finance.yahoo. com, 2019). Les deux équations sont exécutées pour chaque date de la période choisie.

Le tableau 1 montre le rendement quotidien moyen des entreprises, un écart-type des rendements, une valeur minimale des rendements et une valeur maximale des rendements pour cet exemple.

Tableau 1. Rendement moyen partagé et écart type des rendements

La moyenne correspondante est de -0,0006 et l'écart type de 0,0355 des retours pour les titres de sécurité uniques sélectionnés KAZ Minerals. De plus, la variance des rendements est de 0,0013. En outre, cela devrait certainement être souligné que dans les travaux de recherche de Vee, DNC et Gonpot, P. N (2014), les rendements des actions kazakhs ont montré une valeur significative en volatilité, mais l'estimation était liée à l'indice de la Bourse du Kazakhstan en pré et en après la période 2008. En outre, il convient de mentionner que la valeur maximale parmi les rendements est de 0,0998, ainsi que la valeur minimale parmi les rendements est de -0,2829 dans la distribution des pertes. Le tableau 2 présente les valeurs maximales et minimales entre le cours de clôture ajusté (KAZ.L) en livre sterling (GBP) négocié à la Bourse de Londres du 23 mars 2018 au 22 mars 2019.

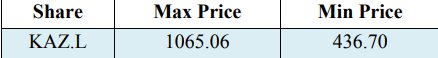
Tableau 2. Cours de l'action KAZ Minerals maximum et minimum en GBP

L'étape suivante est l'évaluation de la valeur à risque (VaR) et de la valeur conditionnelle à risque (CVaR) pour le niveau de confiance - 0,99, 0,972 et 0,95. Les valeurs sont révélées dans le tableau 3.

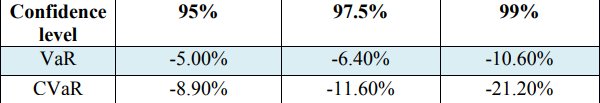
Tableau 3. Valeurs VaR et CVaR des rendements

La taille de l'échantillon de la simulation est prise à 252 unités du 23 mars 2018 au 22 mars 2019 pendant un an.

Discussionion

Dans le rapport, les équations VaR et CVaR démontrent la valeur crédible dans le cas des modèles d'estimation d'un cours de bourse de la société kazakhe à court terme. Avec ces valeurs d'une part, les deux méthodes présentent des résultats adéquats pour évaluer la valeur des menaces pour le portefeuille d'investissement (Linsmeier, TJ et Pearson, ND 2000; Lechner, LA et Ovaert, TC 2010).

De plus, selon les résultats du tableau 2, l'avis suivant est simple: les valeurs de CVaR sont plus massives par rapport aux valeurs de VaR pour toutes les mesures de niveau de confiance. On peut l'expliquer par le fait que le CVaR prend le risque moyen du portefeuille choisi, par conséquent, il est plus sensible en queue de la répartition des pertes que la VaR. Cela prouve une fois de plus que le CVaR est un risque cohérent (Acerbi C. et Tasche D., 2002, cité dans Capiński, MJ 2015; Rockafellar, RT et Uryasev, S. 2000). Par exemple, en ce qui concerne l'adéquation des deux modèles d'estimation, avec un niveau de confiance de 99%, la VaR et le CVaR illustrent le pourcentage significatif de perte résultant des rendements du stock. Pour être précis, il pourrait être détecté que la VaR est de -10,60% et la CVaR de -21,20%. Il est assez clair la raison des mesures colossales de CVaR avec un niveau de confiance donné de 99% en raison du fait que la fourchette de cours des actions au cours de la période, le prix maximum est de 1065,06 GBP, le prix minimum des actions est de 436,70 GBP, respectivement.

Conclusion

Après avoir examiné tout ce qui précède, il convient évidemment de mentionner à nouveau que l'objectif du rapport est de démontrer l'estimation de la valeur de la perte possible pour la société kazakhe (KAZ Minerals) sur une période allant du 23 mars 2018 au 22 mars 2019. formé sur les équations de la valeur à risque (VaR) et de la valeur conditionnelle à risque (CVaR). Les performances de la simulation sont comparées entre elles sur la même période. Les résultats montrent la valeur significative de chaque méthode et prouvent les travaux antérieurs sur le même domaine que CVaR a des mesures plus précises par rapport à VaR (Acerbi C. et Tasche D., 2002, cité dans Capiński, MJ 2015; Rockafellar, RT, et Uryasev, S.2000).

Malgré les critiques, la VaR est un outil répandu dans toutes les institutions financières à ce jour et il existe un large éventail de sa version de modification. En raison des obstacles du calcul complexe dans la recherche approfondie, l'expérience se fait en utilisant Microsoft Excel au lieu d'utiliser un langage de programmation comme Python, ainsi que les résultats sont révélés dans le rapport. Les résultats de l'essai peuvent servir de base à d'autres travaux sur l'utilisation d'une mesure d'évaluation complexe du risque pour le portefeuille dans l'industrie boursière, l'industrie des assurances et l'industrie des investissements.