Sur l'application de la théorie des processus ARMA dans la pratique de l'ingénierie

Ci-dessous, nous dirons quelques mots sur l'alternative en temps discret aux modèles mathématiques sous la forme d'équations différentielles linéaires, qui est généralement connue mais plutôt inattendue pour les ingénieurs, à savoir les modèles autorégressifs - moyenne mobile et perspectives très inhabituelles pour une telle modélisation, dont les capacités dépassent considérablement ce que vous avez l'habitude d'obtenir de LDU.

La liste des capacités potentielles de la technologie comprend l'analyse des systèmes avec une perturbation entrante inaccessible à l'observation, la détermination des propriétés de résonance de ces systèmes, le spectre et le processus d'excitation externe, l'estimation spectrale des processus par leurs courtes réalisations, la modélisation du comportement des systèmes à une faible fréquence d'échantillonnage dans le temps, etc.





Les procédés ARMA, bien connus des économistes (plus précisément, des «économétriciens»), sont beaucoup moins connus des spécialistes de la régulation automatique et, à mon avis, ne sont quasiment jamais utilisés par les ingénieurs mécaniciens et les ingénieurs radioélectroniques, notamment les «old school». L'article tente d'indiquer certains domaines d'application possibles de la théorie ARMA dans la pratique de l'ingénierie.
En bref, simplifié, pour ceux qui ne connaissent pas le sujet, dont il s'agit en fait. Le processus stochastique à temps continu x (t) pour des raisons "numériques" évidentes "correspond en pratique généralement à la séquence à temps discret x [i] avec l'intervalle d'échantillonnage Δt.
En principe, pour tout processus x [i] une représentation de la forme est possible

x [i] - a ₁ · x [i-1] - a ₂ · x [i-2] - ... - a _p · x [ip] = b ₀ · f [i] + b ₁ · f [i- 1] + ... + b _q · f [iq] (1),

où a _k et b _k sont des coefficients constants (pour ce modèle), appelés modèle de moyenne mobile à autorégression avec l'ordre d'autorégression p et la moyenne mobile q. ou un modèle ARMA (p, q), f [i] est une sorte de processus «entrant», dont un peu plus bas. Souvent (1) est écrit sous une forme légèrement différente (6).
Fondamentalement, c'est juste un filtre numérique qui a à la fois des parties AR récursives et des parties MA non récursives.
Il existe une correspondance entre les modèles ARMA (p, q) et les systèmes linéaires (par exemple mécaniques), par exemple, décrits par l'équation différentielle linéaire bien connue de la forme


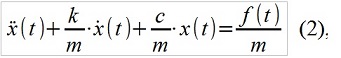
où m, c, k est la masse, la rigidité et l'amortissement du système mécanique, f (t) est la force externe. L'homologue ARMA ressemble à ceci:

x [i] - a ₁ · x [i-1] - a ₂ · x [i-2] = b ₁ · f [i-1] (3),

les coefficients du modèle peuvent être trouvés assez facilement à travers les valeurs propres λ ₁ et λ ₁ * (par souci de concision, le cas "oscillant" est considéré) du système linéaire et Δt:

a ₁ = z + z *, a ₂ = - z · z *, b ₁ = j (z * -z) · Δt / (2mω ₁ ),

où z = exp (λ ₁ · Δt), λ ₁ = -ε ₁ + jω ₁ , j est l'unité imaginaire, * est la conjugaison complexe

pour référence:

Pour le système d'essai, m = 1 kg, c = 100 N / m, k = 0,75 kg / s, Δt = 0,12 s.,
obtenu le modèle ARMA (2,1)

x [i] - 0,69433x [i-1] +0,91393 x [i-2] = 0,010696f [i-1]

(Une très brève explication de la façon dont (3) est obtenu à partir de (2). La fonction de transition d'impulsion de notre système linéaire, c'est-à-dire la réponse du système à une seule impulsion:



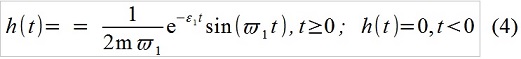
L'enregistrement (2) sous la forme «intégrale» est appelé «convolution» f (t) et h (t), ce qui signifie qu'il implique de considérer l'action extérieure comme une séquence d'impulsions élémentaires. En temps discret, écrivez bien, par exemple, comme ceci:



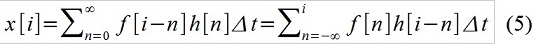
En ajoutant x [i], x [i-1] et x [i-2] en utilisant les facteurs sélectionnés 1, a ₁ et a _{2, ils} réalisent l'annihilation mutuelle des «queues» infinies h [i] - f [i] reste sur le côté droit · H [0] = f [i] · 0 et f [i-1] · h [1] = f [i-1] · b ₁ . Du point de vue de la théorie ARMA, le modèle de dimension infinie de la moyenne mobile MA (∞) est transformé en ARMA (2,1) (bien que certains diront qu'un modèle purement autorégressif AR (2) = ARMA (2,0) a été obtenu par accident.

Remarque 1. Un lecteur familiarisé avec le traitement numérique des processus dira que juste discrétiser h (t) n'est pas très correct - il faut limiter la fonction h (t) en fréquence à 1 / (2Δt) (filtre). Sinon, il y a une erreur de masquage de fréquence. Les graphiques de la réponse en fréquence et de la réponse en phase de notre système, les modèles «analytiques» et ARMA, montrent pourquoi cette erreur dans la plupart des cas d'ingénierie peut très probablement être négligée (Fig. 1) (ici, la réponse en fréquence est sur une échelle logarithmique).

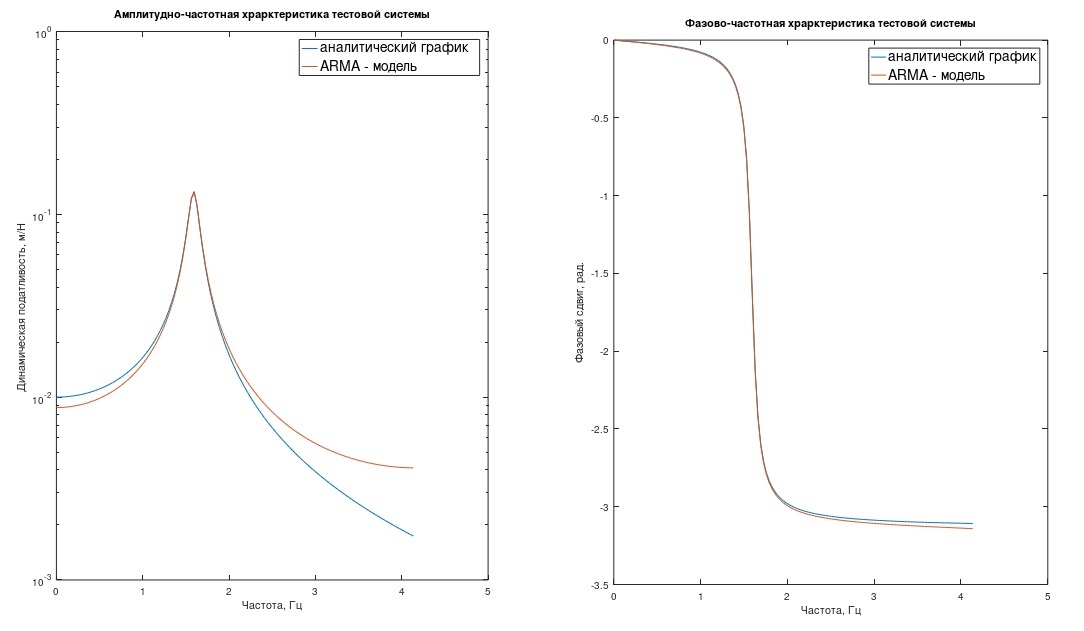
Fig. 1 Réponse en fréquence et réponse en phase du système de test.

Remarque 2. En pratique, l'ordre du modèle ARMA peut être significativement plus grand que l'exemple considéré ci-dessus, en raison, par exemple, de plusieurs degrés de liberté d'un système mécanique ou d'un spectre complexe d'influence externe réelle.

Remarque 3. Très important. Il existe des méthodes (non considérées ici - de nombreux autres articles peuvent être écrits à leur sujet) qui permettent d'estimer les paramètres du modèle ARMA (à savoir, l'ordre du modèle p et q et les coefficients a _k et b _k ) uniquement par le processus résultant x [i], sous l'hypothèse que f [i] est un bruit blanc hypothétique dont la variance peut également être estimée. En général, une telle évaluation est la partie principale de toute la théorie ARMA. Bien que ces méthodes ne diffèrent pas par leur perfection particulière, elles présentent un intérêt considérable.

Maintenant, pourquoi, en fait, tout cela peut (ou pourrait) être appliqué dans la pratique. En plus de la évidence - la construction rapide de sinusoïdes amorties (et non amorties) "manuellement" à partir des deux premiers points et de deux coefficients a ₁ et a ₂ , il y a, à mon avis, des applications plus sérieuses de ces modèles dans la pratique de l'ingénierie.

1. Eh bien, en fait, pour la simulation du fonctionnement du système - nous donnons un vrai signal externe f [i] à l'entrée, nous obtenons x [i] à la sortie:

x [i] = a ₁ · x [i-1] + a ₂ · x [i-2] + ... + a _p · x [ip] + b ₀ · f [i] + b ₁ · f [i- 1] + ... + b _q · f [iq] (6)

Le modèle ARMA fait mieux face à la tâche que le modèle à différences finies, cependant, cela n'est perceptible qu'à de grands intervalles d'échantillonnage Δt. (sur la figure 2, Δt = 0,12 s (à gauche) et 0,03 s). Dans quels cas, il est logique de jouer avec ARMA - vous décidez.

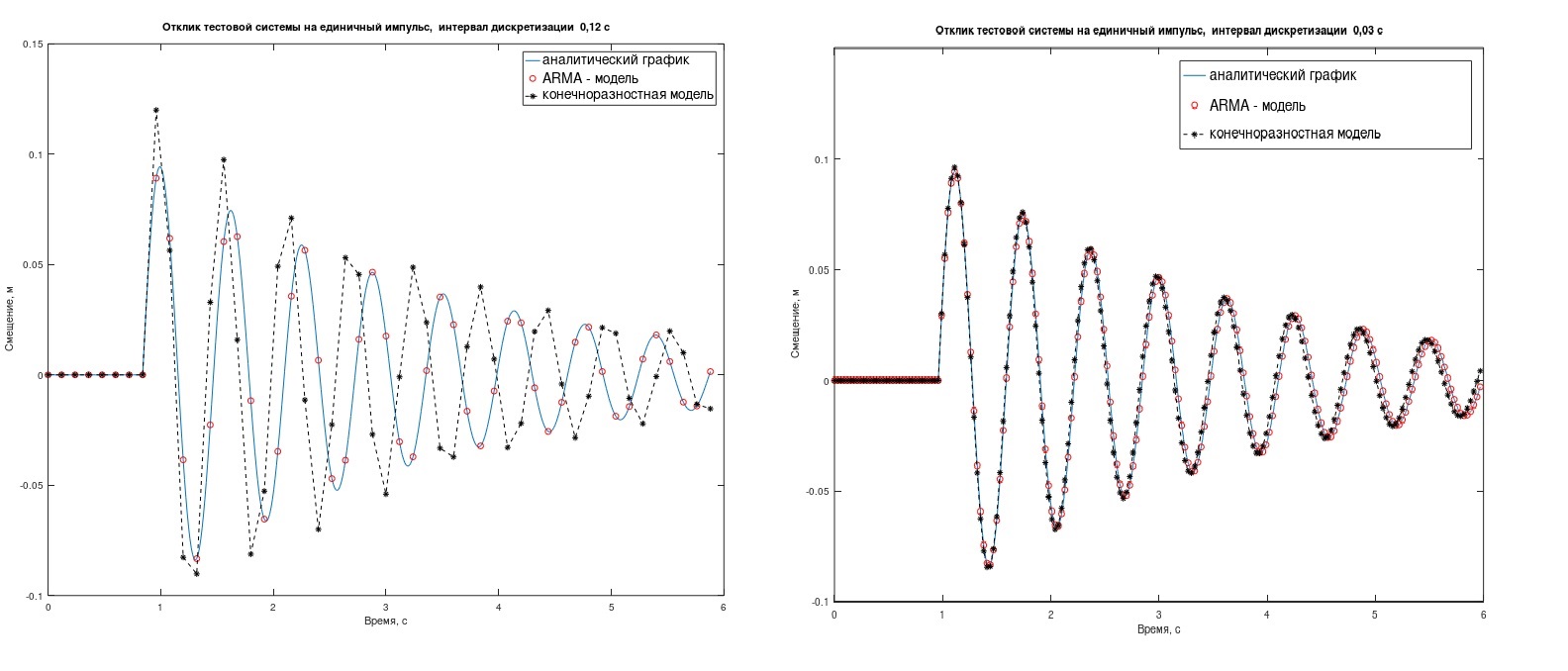
fig. 2. La réponse des systèmes de test à une seule impulsion.

2. Pour l'estimation spectrale, en particulier lorsque la longueur de mise en œuvre du processus stationnaire est insuffisante pour l'observation. Il s'agit peut-être de l'application d'ingénierie la plus connue des modèles ARMA. Puisqu'un certain filtre numérique et la variance du bruit blanc y entrant seront obtenus pour le processus à l'étude, la tâche de construire une estimation de la PSD est résolue de manière évidente. En effet, il est possible d'obtenir extérieurement des graphes SPM très "lisses" et en même temps de créer une impression de haute résolution. L'amélioration attendue de l'évaluation est associée au fait que le chercheur apporte des informations externes sur la nature du processus à la construction de l'évaluation - généralement en définissant un ordre de modèle connu.
En bref, vous devez savoir à quoi devrait ressembler approximativement ce PSD. Les études «exploratoires» de cette implémentation en utilisant des méthodes classiques ne peuvent pas faire grand-chose, se référant principalement à des études classiques (basées sur la FFT) de nature similaire, mais des réalisations significativement plus longues. Il y a un risque d'erreurs grossières.

3. Pour l'analyse des propriétés de résonance du système et du spectre de l'action extérieure, dans le cas où le véritable effet extérieur n'est pas disponible pour l'observation. Comme déjà noté, il est possible, connaissant le processus x [i], de déterminer tous les coefficients du modèle a _k et b _k (et la variance du bruit blanc entrant). En les utilisant, en déterminant les racines de deux polynômes avec les coefficients correspondants, il est facile de trouver p «pôles» et q «zéros» du modèle (λ _k et μ _k ) et de construire sa fonction de transfert - vous ne pourrez probablement même pas utiliser le formulaire ARMA (ici donné), et sous la forme «analytique» habituelle - comme nous l'avons vu ci-dessus (Fig. 1), la différence est faible. Par exemple, pour p = 5, q = 3 (en faisant abstraction des restrictions existantes, apparemment, sur le rapport de p et q), en option, nous avons:



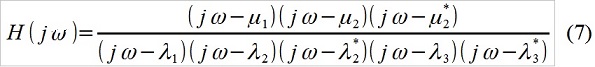
Tout est très, très simplifié, bien sûr. Sur la base de la nature connue de l'objet étudié (par exemple, ce sont des tests polygonaux de la douceur de roulement de la voiture) et de l'impact externe (microprofil de la route), le chercheur a décidé de réécrire la fonction de transfert, par exemple, comme ceci:




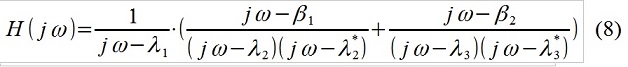
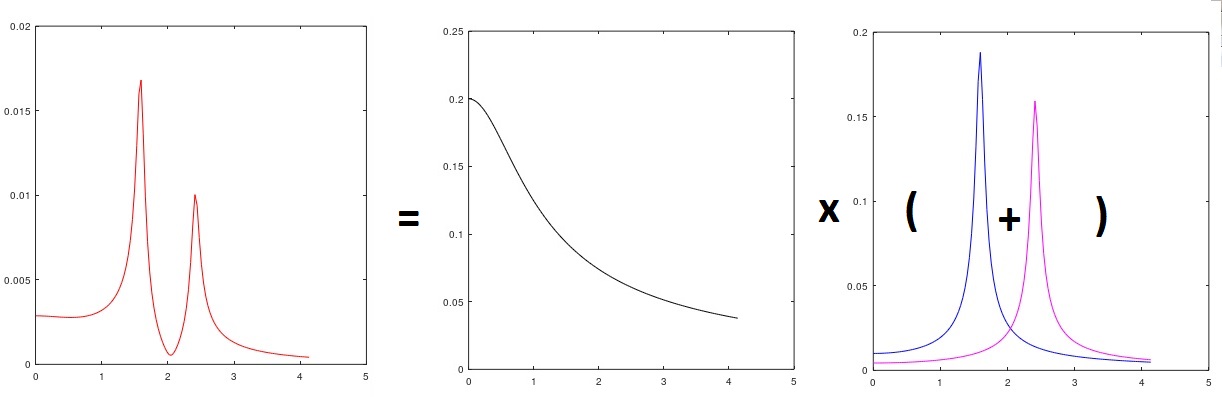
Fig.3 Analyse du spectre du signal avec attribution de la perturbation entrante

et commenté - la partie du modèle associée à λ ₁ est évidemment (jusqu'à la quadrature et la multiplication par la variance du bruit blanc hypothétique entrant) le microprofil "rose" de la route (Fig. 3) (c'est-à-dire que nous avons identifié un spectre inconnu de réel le signal d'entrée - sélectionné manuellement - il semble être "similaire"), λ ₂ et λ ₃ sont les propriétés de résonance du corps sur la suspension (éventuellement modes de vibration longitudinal-angulaire et vertical). Le principal problème sera, bien entendu, de déterminer les paramètres du modèle ARMA. Pour ce qui vient d'être décrit, vous pouvez parfois, sans ARMA, "ramper" à l'ancienne (quoique sous forme électronique) en fonction du graphique de densité spectrale et mesurer la largeur de crête au niveau de -3 dB, etc., ou appliquer une courbure, parfois même avec beaucoup de succès .

3. Pour la prédiction linéaire x [i]. Apparemment, la principale application de l'ARMA est celle des économétriciens. On peut voir à partir de (6) que si les coefficients du modèle ont été estimés en utilisant les méthodes décrites ci-dessus, la valeur suivante x [i] peut être estimée précise à un bruit blanc hypothétique inaccessible à l'observation b ₀ · f [i], la variance de ce bruit blanc est estimée avec les coefficients du modèle. Habituellement, dans ce cas, un ajustement dynamique (en temps réel) des paramètres du modèle est implicite. Apparemment, il peut être utile dans les systèmes de réduction active des vibrations et du bruit. Les spécialistes TAP connaissent le mieux.

4. Pour restaurer un processus inaccessible qui ne peut pas être observé. Lors de la division du modèle en parties, comme indiqué ci-dessus dans la section 3, sur la base des connaissances sur la nature du processus à l'étude, il est possible d'évaluer séparément le spectre de la perturbation entrante, et séparément, les propriétés oscillatoires du système physique (séparer le modèle en parties). Vous pouvez aller plus loin - créer un filtre (modèle ARMA, l'inverse du modèle d'origine) qui relie la sortie du système à l'entrée, et avec son aide du processus résultant x [i] obtenir une implémentation temporaire de la perturbation entrante. Par exemple, essayez de restaurer un signal non déformé enregistré avec des distorsions linéaires précisément inconnues par un équipement qui n'est pas disponible pour une étude distincte (par exemple, obtenu par télémétrie).

Sur la base de mes humbles connaissances, j'exprimerai donc un tel jugement subjectif. L'applicabilité des technologies ARMA aux problèmes d'ingénierie dépend fortement de la perfection des méthodes d'estimation des paramètres de ces modèles à partir du signal résultant, ou plutôt, à mon avis, est fortement limitée par l'imperfection de ces méthodes. L'accumulation d'expérience dans l'application de l'ARMA en ingénierie semble avoir du sens, principalement, en prévision d'une «percée» très probable dans ce domaine.