Préface

Je pense que nous devons expliquer brièvement pourquoi tout à coup un sujet aussi banal avec le calcul du budget énergétique et pourquoi exactement les satellites CubeSat? Eh bien, tout est assez simple ici: ma courte pratique d'enseignement a montré (pour moi) que ce sujet, bien que basique, était loin d'être compris par tout le monde la première fois, et d'ailleurs, il avait plusieurs questions qui n'étaient pas évidentes en première lecture. De plus, il semblerait que sur ces choses de base, ils publient toujours des articles dans IEEE et cela est loin d'être fait par les étudiants . Pourquoi exactement CubeSat? C'est encore plus simple ici: le format satellite est intéressant (le fait même de l'existence de micro et nanosatellites, comme il s'est avéré, plonge beaucoup dans un état de choc court), et donc il est très adapté à des fins éducatives.

La simulation sera effectuée en python 3 pour les mêmes raisons que celles que j'ai exprimées dans ma précédente publication . Nous allons considérer le cas de l'orbite basse (LEO - Low Earth Orbit), et calculer, en fait, le rapport signal / bruit (SNR - Rapport signal / bruit) à l'entrée du récepteur via une liaison descendante (DL - Down Link). Nous utiliserons plusieurs répertoires en accès libre et créerons des graphiques pour plus de clarté.

Tous les codes sources sont disponibles dans mon référentiel GitHub , j'invite toutes les personnes intéressées à le lire! Je serai très reconnaissant pour la révision du code et les critiques constructives!

C'est parti!

Quelles formules allons-nous calculer?

Tout d'abord, bien sûr, il s'agit d'une formule bien connue pour le rapport signal / bruit sur une échelle logarithmique (en décibels, simplement) pour tout le monde (impliqué dans le sujet), où nous prenons en compte toutes les pertes et amplifications possibles avec une certaine quantité d'abstraction:

$SNR = P_t + G_t + G_r + \ eta_ {t} + \ eta_ {r} - L_r - L_t - L - L_ {add} - N [dB] \ qquad (1)$

où - puissance totale du bruit thermique (a une relation connue avec la densité spectrale du bruit $N_0 = kT_ {bruit}$ ) en dBm (décibels par milliwatt), P_t - puissance transmise en dBm, G_t et G_r - gain d'antenne du côté de l'émetteur et du récepteur, respectivement (en dBi - décibels isotropes), $\ eta_ {t}$ et $\ eta_ {r}$ - gain de l'émetteur et du récepteur (en dB), L_t et L_r - pertes dans les départs (en dB), pertes sur le trajet de propagation de l'onde électromagnétique en dB, $L_ {ajouter}$ - pertes supplémentaires (pour ainsi dire, une certaine marge) en dB.

En général, avec les sept premiers termes, c'est plus ou moins clair: ce sont des données de référence. Les choses sont plus intéressantes avec les trois derniers participants au processus.

Puissance de bruit thermique

Comme vous le savez, il n'y a nulle part où se cacher de ce fléau des appareils électroniques, vous ne pouvez que prendre en compte:

$N = 10lg \ left (\ frac {kT_ {noise} B_ {noise}} {10 ^ {- 3}} \ right) [dBm] \ qquad (2)$

où - Constante de Boltzmann $T_ {bruit} = T_a + T_e$ - température de bruit équivalente, T_a - la somme de la perte d'antenne et du bruit (arrière-plan) du ciel, $T_e = T_0 (F_ {sys} -1)$ - température de bruit du récepteur ( T_0 = 290K et $F_ {sys} = 10 ^ {\ frac {NF} {10}}$ - le chiffre du bruit, qui peut être estimé à partir de l'image du bruit ( - facteur de bruit) de l'antenne de réception), et $B_ {bruit}$ - la largeur de la bande de fréquence du bruit. Vous pouvez prendre la bande de bruit égale à la bande passante du récepteur lui-même cependant, selon [1, p. 98] la largeur de bande de bruit $B_ {bruit}$ peut être évalué un peu plus précisément $\ gamma B$ où $\ gamma$ - constante de 1,002 à 1,57 (concerne la configuration du récepteur).

Pertes supplémentaires

Ici, vous pouvez soit prendre une sorte d'approvisionnement garanti, glané, en règle générale, dans les mêmes répertoires, soit approfondir et tout calculer vous-même.

Dans cette section, je m'appuie presque entièrement sur le bon vieux manuel Cantor, à savoir cette partie [1, p. 88-96]. Si les lecteurs ont des sources faisant autorité plus pertinentes - veuillez partager, je pense que cela sera utile à tout le monde.

Ce à quoi nous prêtons principalement attention:

Perte due à la réfraction et à l'inexactitude du pointage de l'antenne ( Perte du faisceau d'antenne )

Sont désignés comme $L_b = 10log_ {10} (1+ (2 \ theta / \ theta_ {0.5}) ^ 2)$ où $\ thêta$ - largeur de faisceau et $\ theta_ {0,5}$ - la largeur du faisceau à mi-puissance, et dépend, peu importe la difficulté de deviner, des caractéristiques de certains dispositifs d'antenne:

Effets de la phase atmosphérique

Si vous croyez aux classiques, ces pertes affectent principalement le taux de transfert de données en raison de la bande passante du récepteur, car il est conseillé de choisir la bande conformément au tableau 1 [1, p. 91]. Pour éviter la distorsion de phase.

Tab. 1. Bande passante maximale du récepteur pour différentes plages.

Fréquence porteuse, GHz	0,5	1	5	10
Bande passante du récepteur (B), MHz	10	25	270	750

Cependant, il convient de noter que les chiffres sont très impressionnants et souvent non pris en compte, en raison du bruit thermique.

Perte due à un décalage de polarisation d'antenne

Peut être estimé en fonction des coefficients d'ellipticité $e_1$ et $e_2$ (Je joins une coupure du livre soviétique comme figure 1).

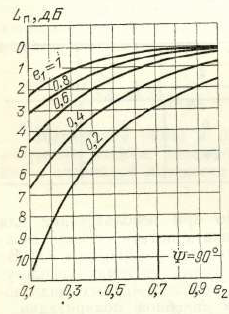
Fig.1. Dépendance des pertes dues à l'inadéquation de la polarisation entre les antennes d'émission et de réception sur l'ellipticité. [1, p. 93]

Cependant, je suis tombé sur ce paramètre comme référence. Par exemple, lors du calcul du budget énergétique du NanoCom AX100, la perte de polarisation est de 3 dB (la perte atmosphérique est de 2,1 dB, la perte ionosphérique est de 0,4 dB).

Atténuation atmosphérique

Nous pouvons évaluer ce paramètre intéressant soit selon les recommandations de l'UIT , soit le calculer nous-mêmes. Heureusement, il existe des bibliothèques spéciales comme celle-ci .

Atténuation le long du chemin de propagation des ondes électromagnétiques (perte de chemin)

Sans plus tarder, nous appliquons la formule Friis pour commencer :

$L = 20lg \ frac {\ lambda} {4 \ pi d} [dB] \ qquad (3)$

où $\ lambda$ - longueur d'onde électromagnétique (se rapporte de manière connue à la fréquence porteuse $f_0 = \ frac {c} {\ lambda}$ , Est la vitesse de l'onde électromagnétique (la vitesse de la lumière, si elle est plus simple)), et - la distance entre les satellites et la station au sol.

Et nous arrivons ici, peut-être, à la question la plus intéressante: quelle distance devons-nous prendre pour les calculs? Comme déjà mentionné dans l'introduction, nous envisageons les satellites LEO, ce qui signifie que notre satellite supposé se déplace par rapport à la Terre (contrairement au cas géostationnaire, dans lequel le satellite, pour ainsi dire, est suspendu sur un point).

Vous pouvez, bien sûr, tout simplifier autant que possible en prenant le schéma comme base (Fig. 2), lorsque l'on suppose que l'orbite du satellite de communication se situe, grosso modo, «au-dessus de la tête» de notre station au sol.

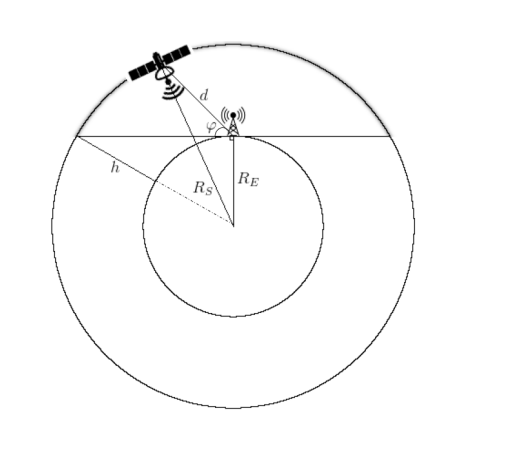
Fig. 2. Description schématique de la trajectoire du CubeSat en orbite terrestre basse [2].

Ensuite, la distance peut être calculée par la formule:

$d = \ sqrt {(R_E + h) ^ 2-R_E ^ 2cos ^ 2 \ phi} - R_Esin \ phi \ qquad (4)$

où R_E - il y a, en fait, le rayon de la Terre, - la hauteur de l'orbite du satellite, et $\ phi$ - angle d'élévation.

Cependant, vous pouvez vous étirer un peu plus, revenir au classique (déjà différent) [3, p.110-123] et calculer tout déjà par rapport aux coordonnées géographiques réelles de la station au sol (
$lat_ {gs}$ et $long_ {gs}$ ) et la position réelle du satellite (nœud ascendant instantané - $L_ {node}$ et pôle orbital - pôle orbital instantané ) Préparez-vous, il y aura beaucoup de trigonométrie:

$d_ {min} = R_E \ frac {\ sin \ lambda_ {min}} {\ sin \ eta_ {min}} \ qquad (5)$

où $\ sin \ lambda_ {min} = \ sin (90 ^ 0 - i) \ sin (lat_ {gs}) + \ cos (90 ^ 0 - i) \ cos (lat_ {gs}) \ cos (long_ {gs} - (L_ {nœud} - 90 ^ 0))$ - angle central minimal de la Terre, $\ eta_ {min} = arctan \ frac {\ sin \ rho \ sin \ lambda_ {min}} {1 - \ sin \ rho \ cos \ lambda_ {min}}$ - angle de nadir minimum, $\ rho = arcsin \ frac {R_E} {R_E + h}$ Est le rayon angulaire de la Terre. La distance maximale peut être calculée par:

$d_ {max} = R_E \ frac {\ sin \ lambda_ {max}} {\ sin \ eta_ {max}} \ qquad (6)$

où $\ sin \ eta_ {max} = \ sin \ rho \ cos \ epsilon_ {min}$ et $\ lambda_ {max} = 90 ^ 0 - \ epsilon_ {min} - \ eta_ {max}$ ( $\ epsilon_ {min}$ - angle d'élévation minimum du satellite).

Pour résumer un bref résumé des paramètres :

Que choisissons-nous comme points de départ : fréquence porteuse, altitude en orbite (peut-être la position du satellite et les coordonnées géographiques de la station au sol - dépend de la précision que nous voulons obtenir);
Nous trouvons des paramètres dépendants de l'équipement et réglables : puissance transmise, largeur de bande du récepteur;
Nous trouvons des données de référence : gain et perte d'antenne, gain et perte du feeder, température du bruit, perte supplémentaire.

Nous simulons ce qui s'est passé

En tant que source de paramètres techniques pour l'évaluation de la liaison descendante, nous avons des exemples réels d'émetteurs-récepteurs et d'antennes pour les satellites CubeSat, tels que le NanoCom AX100 et le NanoCom ANT430 . Pour des bandes passantes plus importantes, il est bien sûr préférable de considérer la bande S. L' antenne patch NanoCom ANT2000 et l'émetteur-récepteur NanoCom SR2000 sont disponibles pour cette gamme.

Nous commençons à vérifier ce qui s'est passé.

from SmallSatLB import * import pandas as pd

Toute logique est conditionnellement divisée en deux options: «tirant d'eau» , dans lequel la formule (4) est utilisée pour calculer la distance; et «précis» , dans lequel les formules (5) et (6) sont utilisées.

«projet»

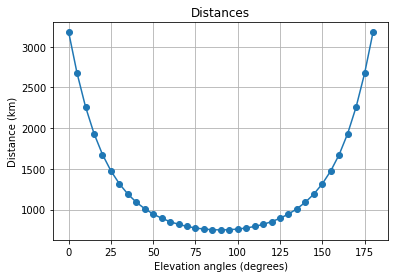
 l_d = LinkBudget(750*1e3, 'draft') #   (   ) d = l_d.distance() #   phi = np.pi*np.array(range(0,181,5))/180 #     plt.plot(180*phi/np.pi, d*1e-3, '-o') plt.title('Distances') plt.xlabel('Elevation angles (degrees)') plt.ylabel('Distance (km)') plt.grid()

 snr, EIRP = l_d.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) #  SNR plt.title('Expected SNRs') plt.xlabel('Elevation angles (degrees)') plt.ylabel('SNR (dB)') plt.legend() plt.grid()

La beauté!

«précis»

 l_p = LinkBudget(750*1e3, 'precise',\ L_node = 100+90, incl = 90 - 61.5,\ lat_gs = 22, long_gs = 200, eps_min = 5) snr, EIRP = l_p.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) print(min(snr)) print(max(snr))

 >>> 5.556823874020452 >>> 8.667000351847676

En général, ici: nous avons un petit outil pour les "estimations" primaires et les calculs de combien le signal va s'affaiblir, alors qu'il va du satellite à la Terre (ou vice versa).
Merci à tous pour votre attention!

Liste de la littérature utilisée :

Kantor L. Ya., Askinazi G.B. Communications et radiodiffusion par satellite: un ouvrage de référence . - Radio et communications, 1988.
Otilia Popescuy, Jason S. Harrisz et Dimitrie C. Popescuz, Designing the Communication Sub-System for Nanosatellite CubeSat Missions: Operational and Implementation Perspectives, 2016, IEEE
Wertz JR, Larson WJ Space Mission Analysis and Design, Space Technology Library. - Microcosm Press et Kluwer Academic Publishers, El Segundo, CA, USA, 1999.

Nous calculons le bilan énergétique d'une ligne radio pour un satellite au format CubeSat