Thermodynamique des trous noirs

Bonne fête de la cosmonautique! Nous avons remis à l'imprimerie un "petit livre sur les trous noirs" . C'est ces jours-ci que les astrophysiciens ont montré au monde entier à quoi ressemblent les trous noirs. Coïncidence? Nous ne pensons pas;) Alors attendez, bientôt un livre étonnant paraîtra, écrit par Stephen Gabser et Frans Pretorius, traduit par le merveilleux astronome Pulkovo alias Astroded Kirill Maslennikov, le légendaire Vladimir Surdin a fait une édition scientifique et la Fondation Trajectory a soutenu sa publication.

Extrait "Thermodynamique des trous noirs" sous la coupe.

Jusqu'à présent, nous avons considéré les trous noirs comme des objets astrophysiques qui se sont formés lors d'explosions de supernova ou se trouvent au centre des galaxies. Nous les observons indirectement, mesurant les accélérations d'étoiles proches d'eux. Le célèbre enregistrement des ondes gravitationnelles par le récepteur LIGO le 14 septembre 2015 est devenu un exemple d'observations plus directes des collisions de trous noirs. Les outils mathématiques que nous utilisons pour mieux comprendre la nature des trous noirs sont: la géométrie différentielle, les équations d'Einstein et les méthodes analytiques et numériques puissantes utilisées pour résoudre les équations d'Einstein et pour décrire la géométrie spatio-temporelle générée par les trous noirs. Et dès que nous pourrons donner une description quantitative complète de l'espace-temps généré par le trou noir, du point de vue astrophysique le sujet des trous noirs peut être considéré comme clos. Dans une perspective théorique plus large, il existe encore de nombreuses opportunités de recherche. Le but de ce chapitre est de parler de certaines réalisations théoriques de la physique moderne des trous noirs, dans lesquelles les idées de thermodynamique et de théorie quantique sont combinées avec la théorie générale de la relativité, donnant naissance à de nouveaux concepts inattendus. L'idée de base est que les trous noirs ne sont pas seulement des objets géométriques. Ils ont une température, ils ont une entropie énorme et peuvent présenter des manifestations d'intrication quantique. Notre discussion sur les aspects thermodynamiques et quantiques de la physique des trous noirs sera plus sommaire et superficielle que l'analyse des caractéristiques spatio-temporelles purement géométriques des trous noirs présentée dans les chapitres précédents. Mais ces aspects, et en particulier quantiques, sont une partie essentielle et vitale des études théoriques en cours sur les trous noirs, et nous nous efforcerons de transmettre, sinon des détails compliqués, du moins l'esprit de ces travaux.

Dans la théorie générale classique de la relativité - si nous parlons de la géométrie différentielle des solutions des équations d'Einstein - les trous noirs sont vraiment noirs dans le sens où rien ne peut en sortir. Stephen Hawking a montré que cette situation change complètement lorsque l'on prend en compte les effets quantiques: les trous noirs émettent un rayonnement d'une certaine température, connue sous le nom de température de Hawking. Pour les trous noirs de taille astrophysique (c'est-à-dire des trous noirs des masses stellaires au supermassif), la température de Hawking est négligeable par rapport à la température du fond micro-ondes cosmique - le rayonnement remplissant l'Univers entier, qui, soit dit en passant, peut lui-même être considéré comme une variante du rayonnement de Hawking. Les calculs effectués par Hawking pour déterminer la température des trous noirs font partie d'un programme de recherche plus large dans le domaine appelé la thermodynamique des trous noirs. Une autre partie importante de ce programme est l'étude de l'entropie des trous noirs, qui caractérise la quantité d'informations perdues à l'intérieur d'un trou noir. Les objets ordinaires (comme une tasse d'eau, une barre de magnésium pur ou une étoile) ont également une entropie, et l'une des déclarations centrales de la thermodynamique des trous noirs est qu'un trou noir de cette taille a plus d'entropie que toute autre forme de matière qui peut être logée dans une zone de même taille, mais sans formation de trou noir.

Mais avant de plonger profondément dans une discussion sur les problèmes associés au rayonnement de Hawking et à l'entropie des trous noirs, faisons une rapide excursion dans les domaines de la mécanique quantique, de la thermodynamique et de l'intrication. La mécanique quantique a été développée principalement dans les années 1920, et son objectif principal était de décrire de très petites particules de matière, telles que des atomes. Le développement de la mécanique quantique a conduit à l'érosion de concepts fondamentaux de la physique comme la position exacte d'une particule individuelle: il s'est avéré, par exemple, que la position d'un électron lorsqu'il se déplace autour d'un noyau atomique ne peut pas être déterminée avec précision. Au lieu de cela, les soi-disant orbites ont été attribuées aux électrons, dans lesquels leur position réelle ne peut être déterminée que dans un sens probabiliste. Pour nos besoins, cependant, il est important de ne pas passer trop rapidement à ce côté - probabiliste - des choses. Prenons l'exemple le plus simple: un atome d'hydrogène. Il peut être dans un certain état quantique. L'état le plus simple d'un atome d'hydrogène, appelé l'état fondamental, est l'état avec l'énergie la plus basse, et cette énergie est connue avec précision. Dans un sens plus général, la mécanique quantique nous permet (en principe) de connaître avec précision l'état de tout système quantique.

Les probabilités viennent à la scène lorsque nous posons un certain type de questions sur un système de mécanique quantique. Par exemple, si l'on sait définitivement que l'atome d'hydrogène est à l'état fondamental, on peut se demander: "Où est l'électron?" et selon les lois du quantum
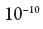
la mécanique, nous arrivons à cette question seulement une certaine estimation de la probabilité, environ quelque chose comme: "l'électron est probablement situé à une distance allant jusqu'à la moitié d'un angström du noyau d'un atome d'hydrogène" (un angström est égal à mètres). Mais nous avons la possibilité, grâce à un certain processus physique, de trouver la position de l'électron beaucoup plus précisément qu'avec un angström. Ce processus, assez courant en physique, consiste à lancer un photon de très courte longueur d'onde dans un électron (ou, comme disent les physiciens, à diffuser un photon sur un électron) - après quoi on peut reconstruire l'emplacement de l'électron au moment de la diffusion avec une précision approximativement égale à la longueur d'onde photon. Mais ce processus va changer l'état de l'électron, de sorte qu'après cela, il ne sera plus dans l'état fondamental de l'atome d'hydrogène et n'aura pas une énergie définie avec précision. Mais pendant un certain temps, sa position sera presque exactement déterminée (précise à la longueur d'onde du photon utilisé pour cela). Une évaluation préliminaire de la position de l'électron ne peut être effectuée que dans un sens probabiliste avec une précision d'environ un angström, mais dès que nous l'avons mesuré, nous savons exactement à quoi il était égal. En bref, si nous mesurons un système quantique-mécanique d'une certaine manière, alors, au moins dans le sens généralement accepté, nous lui donnons «de force» un état avec une certaine valeur de la quantité que nous mesurons.

La mécanique quantique est applicable non seulement aux petits, mais (comme nous le pensons) à tous les systèmes, mais pour les grands systèmes, les règles de mécanique quantique deviennent rapidement très complexes. Le concept clé est l'intrication quantique, dont un exemple simple est le concept de spin (rotation). Les électrons individuels ont un spin, donc en pratique un seul électron peut avoir un spin dirigé vers le haut ou vers le bas par rapport à l'axe spatial sélectionné. Le spin électronique est une quantité observée, car l'électron génère un champ magnétique faible, similaire au champ d'une barre magnétique. Ensuite, un spin pointant vers le haut signifie que le pôle nord de l'électron pointe vers le bas, et un spin pointant vers le bas signifie que le pôle nord «regarde vers le haut». Deux électrons peuvent être mis dans un état quantique conjugué, dans lequel l'un d'eux a un spin dirigé vers le haut et l'autre vers le bas, mais il est impossible de dire lequel des électrons a quel spin. En fait, dans l'état fondamental d'un atome d'hélium, deux électrons sont exactement dans un tel état, appelé spin-singlet, car le spin total des deux électrons est égal à zéro. Si nous séparons ces deux électrons sans changer leurs spins, nous pouvons continuer à affirmer qu'ils sont spin-singlet ensemble, mais nous ne pouvons toujours pas dire quel sera le spin de chacun d'eux individuellement. Maintenant, si nous mesurons l'un de leurs tours et établissons qu'il est dirigé vers le haut, alors nous serons complètement sûrs que le second est dirigé vers le bas. Dans cette situation, nous disons que les dos sont enchevêtrés - pas un en soi n'a une signification définie, alors qu'ensemble ils sont dans un état quantique défini.

Einstein était très préoccupé par le phénomène d'enchevêtrement: il semblait menacer les principes de base de la théorie de la relativité. Considérons le cas de deux électrons dans un état spin-singlet, lorsqu'ils sont éloignés l'un de l'autre dans l'espace. Pour être précis, laissez l'un d'eux prendre Alice et l'autre Bob. Supposons qu'Alice ait mesuré le spin de son électron et a constaté qu'il était vers le haut, et Bob n'a rien mesuré. Jusqu'à ce qu'Alice ait terminé sa mesure, il était impossible de dire quel était le spin de son électron. Mais dès qu'elle a terminé sa mesure, elle savait absolument que le spin de l'électron de Bob était dirigé vers le bas (dans la direction opposée au spin de son propre électron). Est-ce à dire que sa mesure a instantanément transféré l'électron de Bob à l'état lorsque sa rotation est dirigée vers le bas? Comment cela pourrait-il arriver si les électrons sont séparés spatialement? Einstein et ses collègues Nathan Rosen et Boris Podolsky ont estimé que l'histoire de la mesure des systèmes enchevêtrés était si sérieuse qu'elle menaçait l'existence même de la mécanique quantique. Le paradoxe Einstein - Podolsky - Rosen (EPR) formulé par eux utilise une expérience de pensée similaire à celle que nous venons de décrire pour conclure: la mécanique quantique ne peut pas être une description complète de la réalité. Maintenant, sur la base des recherches théoriques qui ont suivi et de nombreuses mesures, une opinion commune a été établie selon laquelle le paradoxe EPR contient une erreur et la théorie quantique est correcte. L'intrication quantique-mécanique est réelle: les mesures des systèmes enchevêtrés seront corrélées, même si ces systèmes sont très éloignés dans l'espace-temps.

Revenons à la situation où nous avons mis deux électrons dans un état spin-singlet et les avons distribués à Alice et Bob. Que dire des électrons avant de prendre des mesures? Que les deux ensemble, ils sont dans un certain état quantique (spin-singlet). Le spin de l'électron Alicin est également susceptible d'être dirigé vers le haut ou vers le bas. Plus précisément, l'état quantique de son électron avec la même probabilité peut être un (spin up) ou un autre (spin down). Maintenant, pour nous, le concept de probabilité prend un sens plus profond qu'auparavant. Avant, nous avons considéré un certain état quantique (l'état fondamental d'un atome d'hydrogène) et avons vu qu'il y avait des questions «inconfortables», telles que «Où est situé l'électron?», Questions dont les réponses n'existent que dans un sens probabiliste. Si nous posions de «bonnes» questions, par exemple: «Quelle est l'énergie de cet électron?», Nous obtiendrions certaines réponses. Maintenant, il n'y a pas de «bonnes» questions que nous pourrions poser sur l'électron d'Alice, dont les réponses ne dépendraient pas de l'électron de Bob. (Nous ne parlons pas de questions stupides comme "Est-ce que l'électron d'Alice a un spin du tout?" - des questions auxquelles il n'y a qu'une seule réponse.) Ainsi, nous devrons utiliser un langage probabiliste pour déterminer les paramètres de l'un des systèmes semi-confus. La certitude ne naît que lorsque nous considérons le lien entre les questions qu'Alice et Bob peuvent poser sur leurs électrons.

Nous avons délibérément commencé avec l'un des systèmes de mécanique quantique les plus simples que nous connaissions: les systèmes de spin des électrons individuels. On espère que les ordinateurs quantiques seront construits sur la base de ces systèmes simples. Le système de spin des électrons individuels ou d'autres systèmes quantiques équivalents sont maintenant appelés qubits (abréviation de "quantum bits"), ce qui souligne leur rôle dans les ordinateurs quantiques, semblable au rôle joué par les bits ordinaires dans les ordinateurs numériques.

Imaginez maintenant que nous avons remplacé chaque électron par un système quantique beaucoup plus complexe avec de nombreux et pas seulement deux états quantiques. Par exemple, ils ont donné des barres de magnésium pur à Alice et Bob. Avant qu'Alice et Bob ne se séparent dans des directions différentes, leurs barres peuvent interagir, et nous conviendrons que ce faisant, elles acquièrent un certain état quantique général. Dès qu'Alice et Bob divergent, leurs barres de magnésium cessent d'interagir. Comme dans le cas des électrons, chaque barre est dans un état quantique indéfini, bien qu'ensemble, comme nous le pensons, elles forment un état complètement défini. (Dans cette discussion, nous supposons qu'Alice et Bob sont capables de déplacer leurs barres de magnésium sans perturber leur état interne, tout comme nous avons précédemment supposé qu'Alice et Bob pouvaient séparer leurs électrons enchevêtrés sans changer leur rotation.) Mais la différence entre cette expérience de pensée et l'expérience avec les électrons est que l'incertitude dans l'état quantique de chaque barre est énorme. Une barre peut très bien acquérir plus d'états quantiques que le nombre d'atomes dans l'univers. C'est là que la thermodynamique entre en scène. Des systèmes définis de manière très imprécise peuvent cependant avoir des caractéristiques macroscopiques bien définies. Une telle caractéristique est, par exemple, la température. La température est une mesure de la probabilité avec laquelle n'importe quelle partie d'un système a une certaine énergie moyenne, une température plus élevée correspondant à une probabilité plus élevée d'avoir plus d'énergie. Un autre paramètre thermodynamique est l'entropie, qui est essentiellement égale au logarithme du nombre d'états que le système peut prendre. Une autre caractéristique thermodynamique qui serait importante pour une barre de magnésium est sa magnétisation totale, c'est-à-dire, en substance, un paramètre qui montre combien plus d'électrons peuvent être dans la barre avec le spin dirigé vers le haut qu'avec le spin dirigé vers le bas.

Nous avons impliqué la thermodynamique dans notre histoire comme un moyen de décrire des systèmes dont les états quantiques ne sont pas exactement connus en raison de leur enchevêtrement avec d'autres systèmes. La thermodynamique est un outil puissant pour analyser de tels systèmes, mais ses créateurs ne s'attendaient pas du tout à une telle application. Sadi Carnot, James Joule, Rudolph Clausius étaient les chefs de file de la révolution industrielle du XIXe siècle et s'intéressaient à leur question la plus pratique: comment fonctionnent les moteurs? La pression, le volume, la température et la chaleur sont la chair et le sang des moteurs. Carnot a découvert que l'énergie sous forme de chaleur ne peut jamais être complètement transformée en un travail utile comme le levage de marchandises. Une partie de l'énergie sera toujours gaspillée. Clausius a apporté la principale contribution à la création de l'idée d'entropie comme outil universel pour déterminer les pertes d'énergie au cours de tout processus associé à la chaleur. Sa principale réalisation a été de réaliser que l'entropie ne diminue jamais - dans presque tous les processus, elle croît. Les processus dans lesquels l'augmentation de l'entropie est appelée irréversible - précisément parce qu'ils ne peuvent pas s'inverser sans diminuer l'entropie. La prochaine étape dans le développement de la mécanique statistique a été faite par Clausius, Maxwell et Ludwig Boltzmann (parmi beaucoup d'autres) - ils ont montré que l'entropie est une mesure du désordre. Habituellement, plus vous agissez sur quelque chose, plus vous vous trompez. Et même si vous avez développé un processus dont le but est de rétablir l'ordre, au cours de celui-ci, plus d'entropie se formera inévitablement qu'elle ne sera détruite, par exemple lorsque la chaleur sera libérée. La grue, qui empile les poutres en acier dans un ordre parfait, crée de l'ordre en termes de l'emplacement des poutres, mais tellement de chaleur sera libérée pendant son fonctionnement que l'entropie totale continue de croître.

Mais encore, la différence entre la vue sur la thermodynamique des physiciens du 19e siècle et la vue associée à l'intrication quantique n'est pas aussi grande qu'il y paraît. Chaque fois qu'un système interagit avec un agent externe, son état quantique est confondu avec l'état quantique de l'agent. Habituellement, cet enchevêtrement conduit à une augmentation de l'incertitude de l'état quantique du système, en d'autres termes, à une augmentation du nombre d'états quantiques dans lesquels le système peut être. En raison de l'interaction avec d'autres systèmes, l'entropie, définie en termes de quantité d'états quantiques disponibles pour le système, augmente généralement.

En général, la mécanique quantique fournit une nouvelle façon de caractériser les systèmes physiques dans lesquels certains paramètres (par exemple, la position dans l'espace) deviennent incertains, tandis que d'autres (par exemple, l'énergie) sont souvent connus exactement. Dans le cas de l'intrication quantique, deux parties fondamentalement séparées du système ont un état quantique commun connu, et chaque partie séparément est un état indéfini. Un exemple standard d'enchevêtrement est une paire de spins dans un état singulet dans lequel il est impossible de dire quel spin est dirigé vers le haut et lequel est vers le bas.L'incertitude de l'état quantique dans un grand système nécessite une approche thermodynamique dans laquelle les paramètres macroscopiques, tels que la température et l'entropie, sont connus avec une grande précision, malgré le fait que le système possède de nombreux états quantiques microscopiques possibles.

Après avoir terminé notre brève excursion dans le domaine de la mécanique quantique, de l'intrication et de la thermodynamique, essayons maintenant de comprendre comment tout cela conduit à comprendre le fait que les trous noirs ont une température. Le premier pas vers cela a été fait par Bill Unruh - il a montré qu'un observateur accélérant dans un espace plat aura une température égale à son accélération divisée par 2π. La clé des calculs d'Unruh est qu'un observateur se déplaçant avec une accélération constante dans une certaine direction ne peut voir que la moitié de l'espace-temps plat. En fait, la seconde moitié se situe au-delà de l'horizon, semblable à l'horizon d'un trou noir. Au début, cela semble impossible: comment un espace-temps plat peut-il se comporter comme un horizon de trous noirs? Pour comprendre comment cela se passe, nous demandons l'aide de nos fidèles observateurs Alice, Bob et Bill.À notre demande, ils s'alignent, Alice se retrouvant entre Bob et Bill, et la distance entre les observateurs de chaque paire est exactement de 6 kilomètres. Il a été convenu qu'à temps zéro, Alice sauterait dans une fusée et volerait vers Bill (et donc depuis Bob) avec une accélération constante. Elle a une très bonne fusée, capable d'accélérer 1,5 billion de fois plus que l'accélération gravitationnelle avec laquelle les objets se déplacent près de la surface de la Terre. Bien sûr, il n'est pas facile pour Alice de résister à une telle accélération, mais, comme nous le verrons maintenant, ces chiffres sont choisis dans un but spécifique; après tout, nous ne faisons que discuter des potentialités, c'est tout. Exactement au moment où Alice saute dans sa fusée, Bob et Bill agitent la main. (Nous avons le droit d'utiliser l'expression "exactement au moment où ...", car alors qu'Alice n'a pas encore commencé à voler,elle est dans le même cadre de référence que Bob et Bill, afin qu'ils puissent tous synchroniser leurs horloges.) Alice, bien sûr, la voit agiter: si elle est dans la fusée, elle le verra plus tôt que cela ne se produirait, si elle est restée où elle était, parce que sa fusée avec elle vole précisément vers lui. Au contraire, elle s'éloigne de Bob, nous pouvons donc raisonnablement supposer qu'elle verra comment il lui fera signe, un peu plus tard qu'elle ne l'aurait vu, si elle était restée à son ancienne place. Mais la vérité est encore plus surprenante: elle ne verra pas du tout Bob! En d'autres termes, les photons qui volent de Bob en agitant à Alice ne la rattraperont jamais, même si elle ne peut jamais atteindre la vitesse de la lumière. Si Bob a commencé à agiter, étant un peu plus près d'Alice, alors les photons qui se sont envolés loin de lui au moment de son départ l'auraient dépassée,et s'il était un peu plus loin, encore plus pour qu'ils ne dépassent pas. C'est en ce sens que nous disons que seule la moitié de l'espace-temps est visible pour Alice. Au moment où Alice commence à bouger, Bob est un peu plus loin que l'horizon qu'Alice observe.

Dans notre discussion sur l'intrication quantique, nous sommes déjà habitués à l'idée que même si un système de mécanique quantique dans son ensemble a un certain état quantique, certaines parties de celui-ci peuvent ne pas l'avoir. En fait, lorsque nous discutons d'un système quantique complexe, une partie de celui-ci peut être mieux caractérisée précisément dans le cadre de la thermodynamique: on peut lui attribuer une température très définie, malgré l'état quantique très indéfini de l'ensemble du système. Notre dernière histoire impliquant Alice, Bob et Bill est un peu similaire à cette situation, mais le système quantique dont nous parlons ici est un espace-temps vide, et Alice n'en voit que la moitié. Nous faisons une réserve que l'espace-temps dans son ensemble est dans son état fondamental, ce qui signifie l'absence de particules en lui (bien sûr, sans compter Alice, Bob,Bill et roquettes). Mais cette partie de l'espace-temps qu'Alice voit ne sera pas à l'état fondamental, mais dans un état confondu avec cette partie qu'elle ne voit pas. L'espace-temps perçu d'Alice est dans un état quantique complexe indéfini caractérisé par une température finie. Les calculs d'Unruh montrent que cette température est d'environ 60 nanokelvins. En bref, alors qu'elle accélère, Alice plonge dans un bain de rayonnement chaud avec une température égale (en unités appropriées) à l'accélération divisée parcaractérisé par la température finale. Les calculs d'Unruh montrent que cette température est d'environ 60 nanokelvins. En bref, alors qu'elle accélère, Alice, pour ainsi dire, plonge dans un bain de rayonnement chaud avec une température égale (en unités appropriées) à l'accélération divisée parcaractérisé par la température finale. Les calculs d'Unruh montrent que cette température est d'environ 60 nanokelvins. En bref, alors qu'elle accélère, Alice, pour ainsi dire, plonge dans un bain de rayonnement chaud avec une température égale (en unités appropriées) à l'accélération divisée par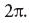



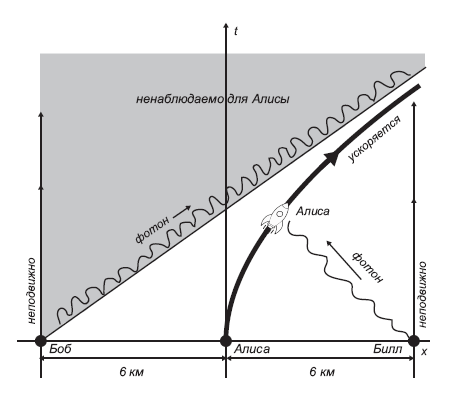
Fig. 7.1.Alice se déplace avec accélération d'un état de repos, tandis que Bob et Bill restent immobiles. L'accélération d'Alice est telle qu'elle ne voit jamais les photons que Bob envoie dans sa direction au moment t = 0. Cependant, elle reçoit les photons qu'au moment t = 0 Bill lui a envoyés. Le résultat est qu'Alice n'est capable d'observer que la moitié de l'espace-temps.

L’étrange des calculs d’Unruh est que, bien qu’ils se réfèrent à l’espace vide du début à la fin, ils contredisent les célèbres paroles du roi Lear «rien ne viendra de rien». Comment un espace vide peut-il être si compliqué? D'où peuvent provenir les particules? Le fait est que selon la théorie quantique, l'espace vide n'est en aucun cas vide. Ici et là, des excitations de courte durée, appelées particules virtuelles, dont l'énergie peut être à la fois positive et négative, apparaissent et disparaissent constamment. Un observateur d'un avenir lointain - appelons-la Carol - qui est capable de voir presque tout l'espace vide, peut confirmer qu'il n'y a pas de particules permanentes dans celui-ci. De plus, la présence de particules à énergie positive dans cette partie de l'espace-temps qu'Alice peut observer,en raison de l'intrication quantique, elle est associée à des excitations d'énergie de signe égale et opposée dans une partie inobservable de l'espace-temps. Toute la vérité sur l'espace-temps vide dans son ensemble est ouverte à Carol, et cette vérité est qu'il n'y a pas de particules. Cependant, l'expérience d'Alice lui dit qu'il y a des particules!

Mais il s'avère que la température calculée par Unruh ne semble être qu'une fiction - ce n'est pas tant une propriété de l'espace plat en tant que telle, mais une propriété d'un observateur connaissant une accélération constante dans l'espace plat. Cependant, la gravitation elle-même est la même force «fictive» en ce sens que «l'accélération» qu'elle provoque n'est rien d'autre qu'un mouvement le long d'une géodésique dans une métrique courbe. Comme nous l'avons expliqué au chapitre 2, le principe d'équivalence d'Einstein est que l'accélération et la gravité sont essentiellement équivalentes. De ce point de vue, il n'y a rien de particulièrement choquant que l'horizon d'un trou noir ait une température égale à la température de l'observateur accélérateur calculée par Unru. Mais peut-on demanderquelle valeur d'accélération devons-nous utiliser pour déterminer la température? En se déplaçant à une distance suffisamment grande du trou noir, nous pouvons arbitrairement affaiblir son attraction gravitationnelle. S'ensuit-il que pour déterminer la température effective du trou noir que nous mesurons, nous devons utiliser la petite valeur d'accélération correspondante? Cette question s'avère plutôt insidieuse, car, comme nous le pensons, la température d'un objet ne peut pas baisser arbitrairement. On suppose qu'il a une valeur finie fixe que même un observateur très éloigné peut mesurer.De quoi avons-nous besoin pour utiliser la petite valeur d'accélération correspondante afin de déterminer la température effective du trou noir que nous mesurons? Cette question s'avère plutôt insidieuse, car, comme nous le pensons, la température d'un objet ne peut pas baisser arbitrairement. On suppose qu'il a une valeur finie fixe que même un observateur très éloigné peut mesurer.De quoi avons-nous besoin pour utiliser la petite valeur d'accélération correspondante afin de déterminer la température effective du trou noir que nous mesurons? Cette question s'avère plutôt insidieuse, car, comme nous le pensons, la température d'un objet ne peut pas baisser arbitrairement. On suppose qu'il a une valeur finie fixe que même un observateur très éloigné peut mesurer.