🧠 ↖️ 🧖🏿 Entropie du Chaos 🤞 💇🏿 👩🏻‍🚒

Présentation

Il y a beaucoup de publications sur Habr qui discutent du concept d'entropie, en voici juste quelques-unes [1 ÷ 5]. Les publications ont été bien accueillies par les lecteurs et ont suscité un grand intérêt. Il suffit de donner la définition de l'entropie donnée par l'auteur de la publication [1]: «l'entropie est la quantité d'informations que vous ne connaissez pas sur le système». Les publications sur le phénomène du chaos sur Habr sont également suffisantes [6–9]. Cependant, la relation entre l'entropie et le chaos dans les deux groupes de publications n'a pas été prise en compte.

Cela est dû au fait que différents domaines de connaissances distinguent différents types de mesures du chaos:

informationnel;
thermodynamique;
différentiel;
culturel.

Les mesures du chaos sont également décrites en tenant compte de leur spécificité, même dans l'un de ces domaines est assez difficile.

En essayant de simplifier la tâche autant que possible, j'ai décidé de considérer la relation entre l'entropie informationnelle et le chaos en utilisant l'exemple de la similitude des régions de passage de l'ordre au chaos sur les diagrammes sous forme de cartographies ponctuelles et sur les graphiques du coefficient d'entropie pour ces régions.

Qu'est-ce qui est arrivé, vous apprendrez en regardant sous le chat.

Les mécanismes de transition de l'ordre au chaos

Une analyse des mécanismes de la transition de l'ordre au chaos dans des systèmes réels et divers modèles a révélé la polyvalence de relativement peu de scénarios de transition vers le chaos. La transition vers le chaos peut être représentée sous la forme d'un diagramme de bifurcation (le terme «bifurcation» est utilisé pour désigner des réarrangements qualitatifs du système avec l'émergence d'un nouveau mode de comportement).

L'entrée du système en mode imprévisible est décrite par une cascade de bifurcations qui se succèdent. La cascade de bifurcations conduit séquentiellement à un choix entre deux solutions, puis quatre et ainsi de suite, le système commence à osciller dans un mode chaotique et turbulent de doublement séquentiel du nombre de valeurs possibles.

Nous considérons les bifurcations du doublement des périodes et l'apparition du chaos dans les cartographies ponctuelles. L'affichage est une fonction qui montre la dépendance des valeurs suivantes des paramètres système par rapport aux valeurs précédentes:

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$

Considérez également la deuxième fonction couramment utilisée:

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

En utilisant des correspondances de points, les objets sont étudiés non pas avec un temps continu, mais avec un temps discret . Lors du passage à l'affichage, la dimension du système à l'étude peut diminuer.

Lors de la modification du paramètre externe \ lambda, les mappages de points présentent un comportement assez compliqué, qui devient chaotique avec un \ lambda suffisamment grand. Le chaos est une récession très rapide des trajectoires dans l'espace des phases.

La bifurcation est une restructuration qualitative du film. Les valeurs du paramètre de contrôle auquel les bifurcations se produisent sont appelées valeurs critiques ou bifurcations.

Pour construire les diagrammes, nous utiliserons les deux listes suivantes:

N ° 1. Pour la fonction:

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$

Liste des programmes

# -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0): x1=(a-1)/a#     def ff(x):#  return a*x*(1-x) def fl(x): return x x=x0;y=0;Y=[];X=[] for i in arange(1,1000,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y plt.title('   \n\ $x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n})$  $\lambda$ =%s  x0=%s '%(a,x0)) plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

No. 2. Pour la fonction

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Liste des programmes

 # -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0): x1=((a-1)/a)**0.5 def ff(x):#  return a*x*(1-x**2) def fl(x): return x x=x0;y=0;Y=[];X=[] for i in arange(1,1000,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y plt.title('   \n\ $x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n}^{2})$  $\lambda$ =%s  x0=%s '%(a,x0)) plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

Évaluer l'impact de la nature de la fonction logistique sur les valeurs critiques

$\ lambda$ considérer les diagrammes avec une fonction

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ Pour ce faire, nous utiliserons le listing n ° 1:

Pour 0 <\ lambda <1 pour

$\ lambda = 0,95$ et x0 = 0,47 on obtient le diagramme:

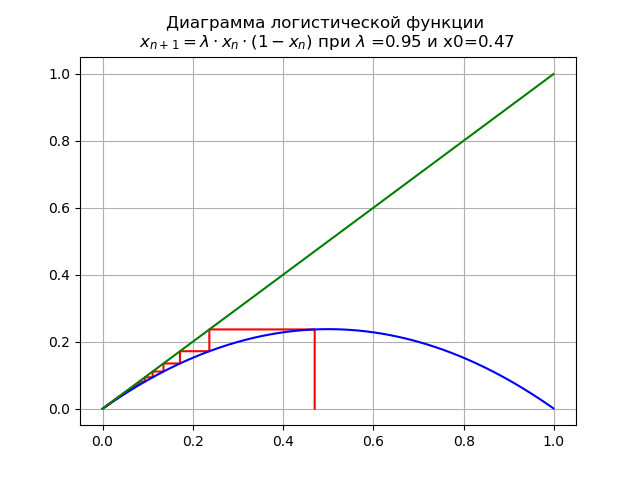
Dans ce cas, la carte a un seul point fixe

$x ^ {*} = 0$
qui est durable.

À

$1 <\ lambda <3$ pour

$\ lambda = 2,5$ x0 = 0,7 on obtient le diagramme:

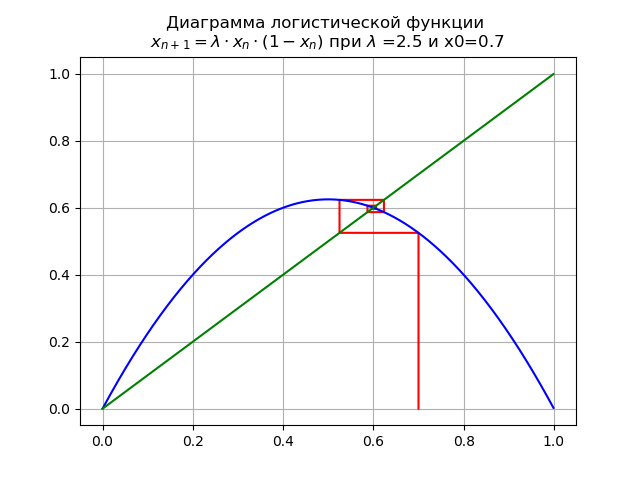
Sur le segment [0, 1], un autre point fixe fixe apparaît

$x_ {1} ^ {*} = 1-1 / \ lambda$

À

$1 <\ lambda <3$ pour

$\ lambda = 2,5$ et x0 = 0,01 on obtient le diagramme:

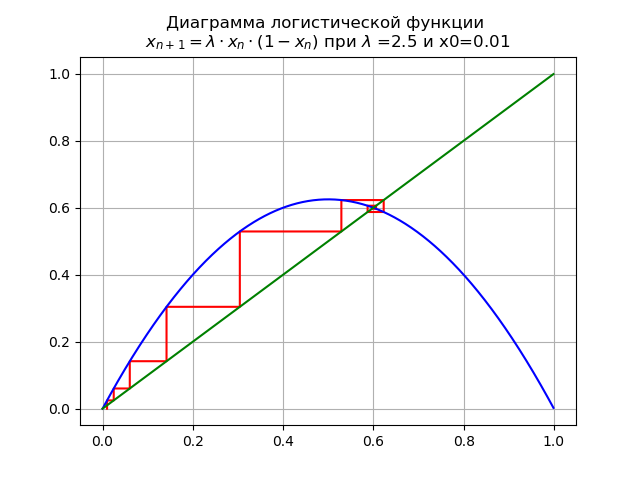
Point fixe

$x ^ {*} = 0$ perd sa stabilité.

À

$3 $ <\ lambda <3,45 $$ pour

$\ lambda = 3,43$ et x0 = 0,7 on obtient le diagramme:

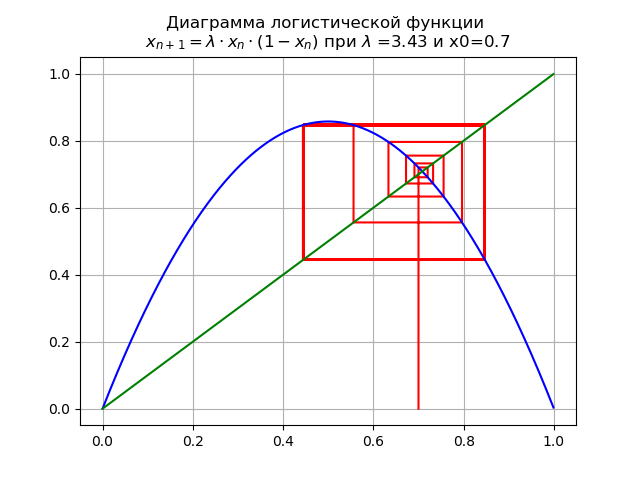
La cartographie subit une bifurcation: point fixe

$x_ {1} ^ {*}$ devient instable et un double cycle apparaît à la place.

À

$3,45 $ <\ lambda <4,0 $$ pour

$\ lambda = 3,55$
et x0 = 0,2 on obtient le diagramme:

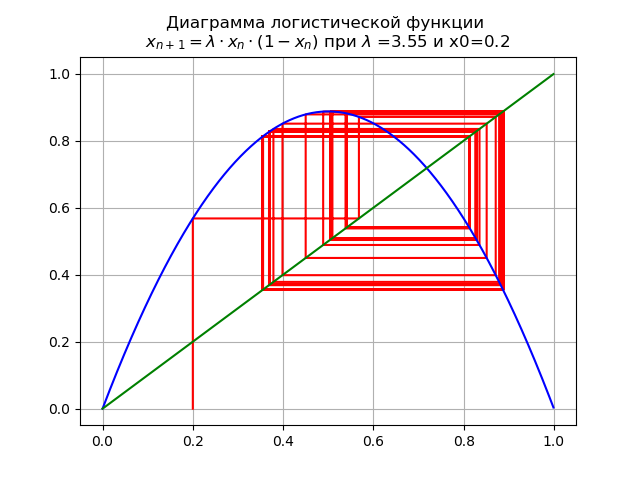
Lors du passage d'un paramètre

$\ lambda$ par la valeur

$\ lambda = 3,45$ , Un cycle de 2 fois devient un cycle de 4, et au-delà.

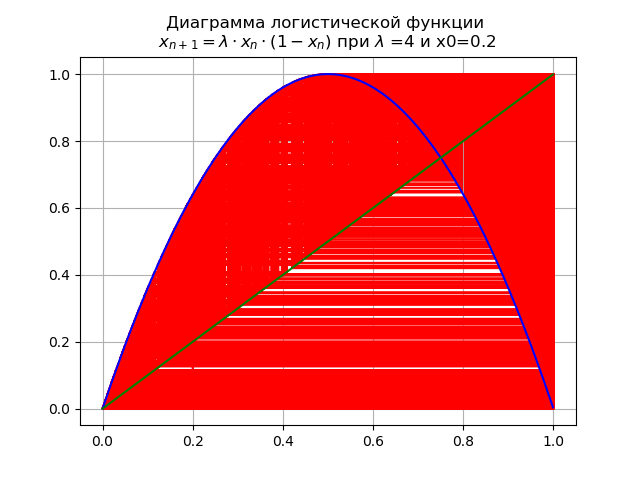
À la valeur finale

$\ lambda = 4$ le système a des cycles instables de toutes les commandes possibles:

Évaluer l'impact de la nature de la fonction logistique sur les valeurs critiques

$\ lambda$ considérer les diagrammes avec une fonction

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$ , pour cela, nous utiliserons la liste n ° 2.

À

$0 <\ lambda <= 1.0$ pour

$\ lambda = 0,5$ et x0 = 0,2:

La cartographie a un seul point fixe

$x ^ {*} = 0$ qui est durable.

À

$1 <\ lambda <= 1.998 ...$ pour

$\ lambda = 1,8$ et x0 = 0,55:

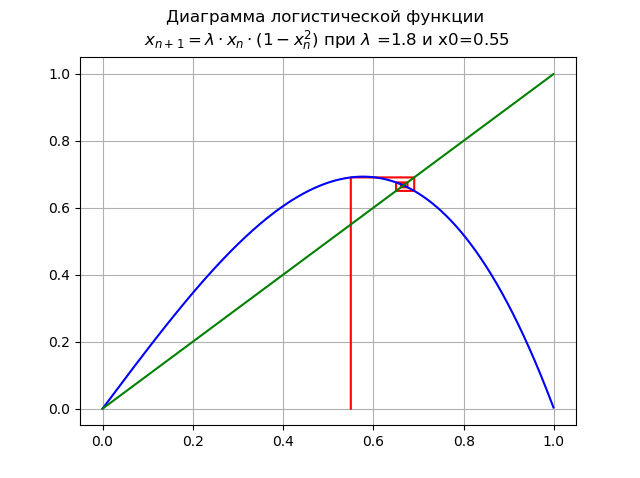
Point

$x ^ {*} = 0$ perd de sa stabilité, un nouveau point stable apparaît

$x_ {1} ^ {*}$

À

$1,99 $ <\ lambda <= 2,235 ... $$ pour

$\ lambda = 2,2$ et x0 = 0,2:

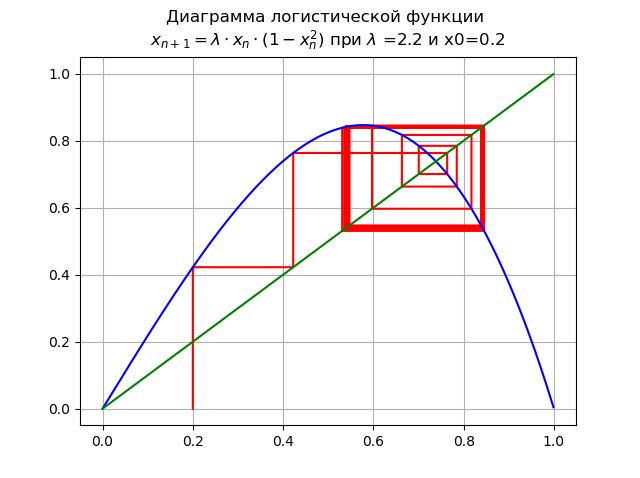
La bifurcation du doublement de la période se produit, un cycle double apparaît. Augmentation supplémentaire

$\ lambda$ conduit à une cascade de bifurcations doublant la période.

À

$2235 $ <\ lambda 2,5980 ... $$ pour

$\ lambda = 2,287$ et x0 = 0,2:

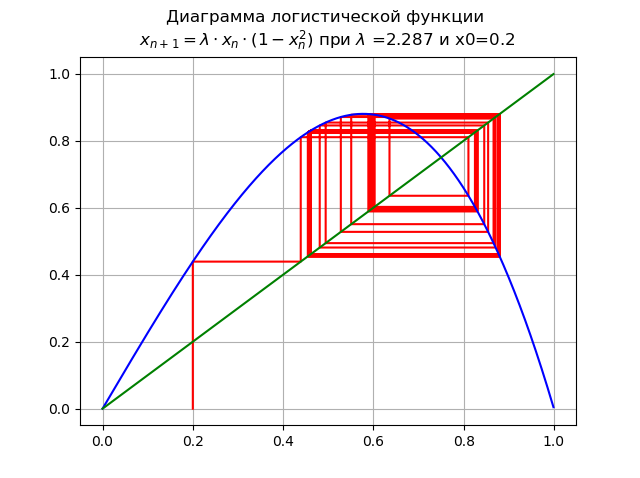
Augmenter

$\ lambda$ conduit à une cascade de bifurcations doublant période.

À

$\ lambda = 2,59$ le système a des cycles instables de toutes les périodes possibles:

Comme le montrent les diagrammes, avec une augmentation de l'ordre de la fonction logistique, l'amplitude du changement

$\ lambda$ diminue.

À l'aide de diagrammes, nous avons tracé le chemin de l'ordre au chaos, tout en définissant les valeurs

$\ lambda$ pour différentes fonctions logistiques. Reste à répondre à la question: comment mesurer le chaos? La réponse à certains des types de chaos énumérés au début de l'article est connue
- l'entropie est une mesure du chaos. Cette réponse peut être entièrement attribuée au chaos de l'information, cependant, quelle entropie est appliquée ici et comment comparer avec la valeur numérique déjà considérée

$\ lambda$ - Je vais essayer de répondre à cette question dans la prochaine partie de l'article.

Entropie de l'information et coefficient d'entropie

Nous considérerons l'entropie binaire des informations pour des événements aléatoires indépendants.

$x$ c

$n$ états possibles distribués avec probabilités

$p_ {i} (i = 1, .., n)$ . L'entropie binaire des informations est calculée par la formule:

$H (x) = - \ sum_ {i = 1} ^ {n} p_ {i} \ cdot log_ {2} (p_ {i})$

Cette valeur est également appelée entropie moyenne du message. Valeur

$H_ {i} = - log_ {2} (p_ {i})$ appelé entropie privée, caractérisant uniquement le i- ème état. Dans le cas général, la base du logarithme dans la définition de l'entropie peut être supérieure à 1; son choix détermine l'unité de mesure de l'entropie.

Nous utiliserons des logarithmes décimaux dans lesquels l'entropie et les informations sont mesurées en bits. La quantité d'informations en bits sera calculée correctement lorsque, par exemple, des variables

$X$ et

$\ Delta$ sera substitué dans les expressions correspondantes pour l'entropie, peu importe où, mais toujours dans les mêmes unités. En effet:

$q = H (x) -H (\ Delta) = log_ {10} \ left (X_ {2} -X_ {1} \ right) -log_ {10} (2 \ Delta) = log_ {10} (\ frac {X_ {2} -X_ {1}} {2 \ Delta})$

où X et

$\ Delta$ doit être dans les mêmes unités.

Une estimation de la valeur d'entropie d'une variable aléatoire à partir de données expérimentales est trouvée à partir d'un histogramme de la relation suivante:

$\ Delta_ {e} = \ frac {1} {2} e ^ {H (x)} = \ frac {d} {2} \ prod_ {i = 1} ^ {m} (\ frac {n} { n_ {i}}) ^ {\ frac {n_ {i}} {n}} = \ frac {dn} {2} 10 ^ {- \ frac {1} {n}} \ sum_ {i = 1} ^ {m} n_ {i} log_ {10} (n_ {i})$

où:

$d$ –Largeur de chaque colonne de l'histogramme;

$m$ - nombre de colonnes;

$n$ - quantité totale de données;

$n_ {i}$ - quantité de données dans

$i$ cette colonne.

Le coefficient d'entropie est déterminé à partir du rapport:

$k_ {e} = \ frac {\ Delta_ {e}} {\ sigma}$

où:

$\ sigma$ - écart type.

L'entropie de l'information comme mesure du chaos

Pour analyser les phénomènes de chaos de l'information en utilisant le coefficient d'entropie, nous créons d'abord un diagramme de branche pour la fonction

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ avec l'application des zones de transition obtenues lors de la construction des histogrammes:

Diagramme de branche

 import matplotlib.pyplot as plt import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(3.58,3.9,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-y[n-1]),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title("   3,6<= $\lambda$ <=3,9") plt.xlabel("r") plt.ylabel("$\lambda$ ") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.show()

Nous obtenons:

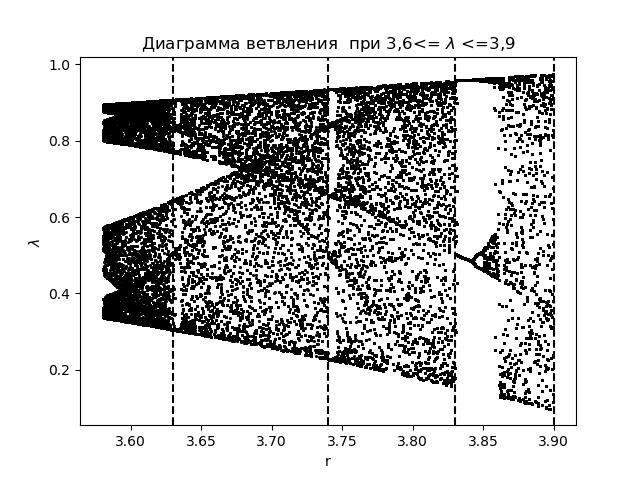
On trace le coefficient d'entropie pour les mêmes zones

$\ lambda$ :

Le graphique du coefficient d'entropie

 import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(3.58,3.9,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-M[i-1,j]) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.title("  ke  3,6<= $\lambda$ <=3,9") plt.plot(arange(3.58,3.9,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.grid() plt.show()

Nous obtenons:

En comparant le diagramme et le graphique, nous voyons un affichage identique des régions sur le diagramme et sur le graphique pour le coefficient d'entropie de la fonction

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ .

Pour une analyse plus approfondie des phénomènes de chaos de l'information en utilisant le coefficient d'entropie, nous créons un diagramme de branche pour la fonction logistique:

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$ avec l'application des zones de transition:

Diagramme de branche

 import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(2.25,2.56,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-(y[n-1])**2),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title("   2.25<=$\lambda$ <=2.56") plt.xlabel("$\lambda$ ") plt.ylabel("y") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.show()

Nous obtenons:

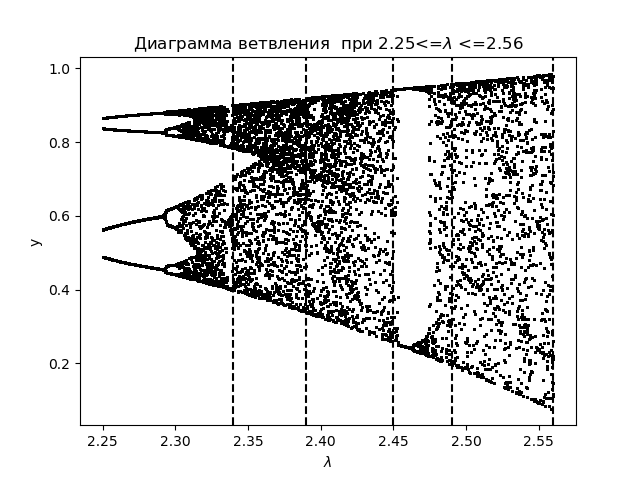
On trace le coefficient d'entropie pour les mêmes zones

$\ lambda$ :

Graphique du coefficient d'entropie

 import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(2.25,2.56,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-(M[i-1,j])**2) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.figure(2) plt.title("  ke  2.25<= $\lambda$ <=2.56") plt.plot(arange(2.25,2.56,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.grid() plt.show()

Nous obtenons:

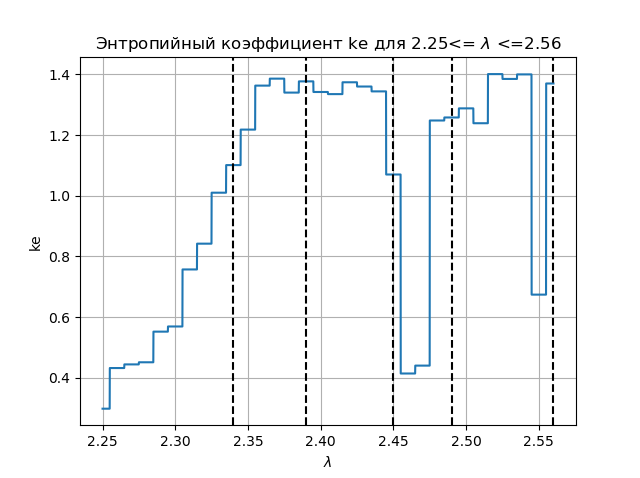
En comparant le diagramme et le graphique, nous voyons un affichage identique des régions sur le diagramme et sur le graphique pour le coefficient d'entropie de la fonction

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Conclusions:

Le problème éducatif est résolu dans l'article: l'entropie informationnelle est-elle une mesure du chaos, et la réponse à cette question est affirmativement donnée par Python.

Entropie du Chaos

Présentation

Les mécanismes de transition de l'ordre au chaos

Entropie de l'information et coefficient d'entropie

L'entropie de l'information comme mesure du chaos

Conclusions:

Les références

More articles: