Sur l'estimation autorégressive de la densité spectrale d'un signal stationnaire

Les méthodes d'estimation spectrale des processus aléatoires stationnaires basées sur la transformée de Fourier rapide (FFT) sont bien connues et largement utilisées dans la pratique de l'ingénierie. Leurs inconvénients incluent, en particulier, une dispersion élevée (faible précision) de l'estimation avec un intervalle d'observation insuffisamment long pour le processus, qui se manifeste visuellement généralement dans un graphique fortement "en retrait" de la densité spectrale de puissance (PSD). L'une des méthodes alternatives d'estimation spectrale est la méthode autorégressive, considérée dans l'exemple ci-dessous, qui est beaucoup moins connue dans la pratique de l'ingénierie. Dans de nombreux cas, la méthode permet d'obtenir relativement facilement une bien meilleure estimation de la PSD (Fig.1), et parfois même des informations plus approfondies sur le processus aléatoire à l'étude.


Fig. 1 Évaluation classique et autorégressive du processus «court» PSD

À des fins de démonstration, un signal à temps discret (séquence) x [i] a été synthétisé. Le signal est modélisé à l'aide d'un modèle ARMA (filtre numérique) simulant les propriétés d'un système mécanique (1) - déplacement du point matériel x (t) dans un oscillateur «simple masse» avec paramètres m = 1 kg, c = 100 N / m, k = 2, 5 kg / s, et par une perturbation de force - bruit gaussien «blanc» (en tenant compte de la discrétisation) f (t) avec une dispersion de 1 N ² , l'intervalle d'échantillonnage dans le temps Δt = 0,12 s.



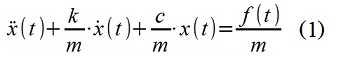
Modèle construit (2). La méthode de construction du modèle a déjà été examinée précédemment.

x [i] - 0,6388 · x [i-1] + 0,7408 · x [i-2] = 0,009667 · f [i-1] (2)

En utilisant (2), une séquence de 50 000 échantillons a été synthétisée, pour laquelle un générateur d'une variable aléatoire aléatoire normalement distribuée () d'un environnement logiciel bien connu a été utilisé.

Une fois la simulation du processus x [i] terminée, les paramètres quantitatifs du modèle (2) sont supposés inconnus - seuls le processus lui-même et, dans une certaine mesure, des informations sur les propriétés du modèle dans les termes les plus généraux sont disponibles pour la recherche.

Une estimation spectrale de la séquence de 50 000 points a été effectuée en utilisant la méthode Welch, la taille du segment a été prise égale à 256 échantillons, la fenêtre de Hamming et un chevauchement de 60% des segments ont été appliqués. L'écart type d'une telle estimation, basé sur le fait que la séquence a une longueur d'environ 200 segments sans chevauchement, peut être approximativement estimé à environ 7%.

De plus, en supposant que dans des conditions réelles de l'expérience, une séquence beaucoup plus courte soit disponible pour la recherche, des études n'ont été menées que sur les 500 premiers échantillons de ce signal.

Une estimation est obtenue par la méthode Welch avec les mêmes paramètres. L'écart type d'une telle estimation est de ~ 70%, une très forte «rugosité» du graphique est perceptible (Fig. 2).


Fig.2. Évaluation de la PSD des processus "long" et "short" par la méthode classique

Sur la base du fait que nous connaissons la forme approximative de la fonction (graphique) du processus SPM (par exemple, sur la base de la nature physique connue du processus - un oscillateur simple masse sous bruit blanc, ou en évaluant des processus similaires pour lesquels des implémentations plus longues sont disponibles), nous avons décidé d'évaluer avec en utilisant le modèle autorégressif du second ordre (AR (2), ou = ARMA (2.0)).

La détermination de l'ordre du modèle est un point très important; une erreur dans l'ordre peut conduire à des erreurs très grossières dans les résultats d'estimation. Il existe des méthodes qui ne sont pas encore prises en compte ici, permettant de déterminer l'ordre du modèle en fonction uniquement du processus analysé.

L'estimation des paramètres du modèle a été effectuée en utilisant les équations de Yule-Walker bien connues pour le processus autorégressif (légèrement modifiées pour simplifier légèrement la structure du script):



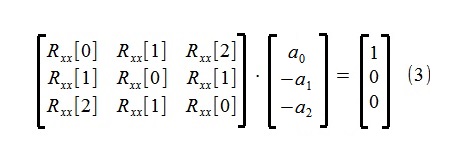
Comme le montrent les équations, pour déterminer les paramètres, seuls les trois premiers membres de la séquence autorégressive Rxx [0], Rxx [1], Rxx [2], qui ont été estimés à partir de la séquence initiale de 500 points x [i] par la méthode du corrélogramme, sont utilisés ~ 4,5%.

(Soit dit en passant, il est clair que les «inconvénients» avant ₁ , a2 ₂ , etc., sont extrêmement gênants. Ils sont apparus en raison de l'utilisation principalement «prédictive» des modèles ARMA dans l'économie, dans leurs sources «d'ingénierie» antérieures Non. Je doute déjà qu'il était nécessaire d'utiliser une telle compréhension des coefficients AR ici.)

En pratique, la matrice de corrélation de (3) a toujours une prévalence diagonale stricte | Rxx [0] | > | Rxx [i] |, y compris en raison de la présence de bruits d'observation, ce qui n'entraîne aucune difficulté de manipulation (trouver une solution (3)).

(Pour clarifier la question de l'ampleur de l'erreur de modélisation statistique, il est intéressant de mentionner, par exemple, l'estimation Rxx [0] = 2.2606e-04 m ² obtenue à partir de 500 échantillons, en comparaison avec le corrélogramme obtenu des estimations de dispersion à partir de 50.000 échantillons, = 2.4238e-04 m ² et l'estimation par l'intégrande de la zone PSD obtenue par la méthode de Welch pour 50 000 échantillons (Fig.2), = 2,4232e-04 m ² )

Après avoir substitué les estimations trouvées Rxx [i], nous avons:



Les paramètres de modèle suivants sont déterminés a ₀ = 11325,9; a ₁ = 7090,1; a ₂ = -8411,5; Comme on peut le voir à partir de (3), la dispersion du bruit blanc hypothétique entrant a été définie = 1 ici, déterminant à la place du gain a ₀ . Une estimation autorégressive de la PSD est construite par la transformée de Fourier sur une séquence de coefficients a ₀ , a ₁ , a ₂ :




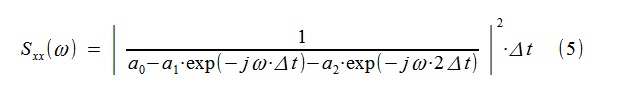
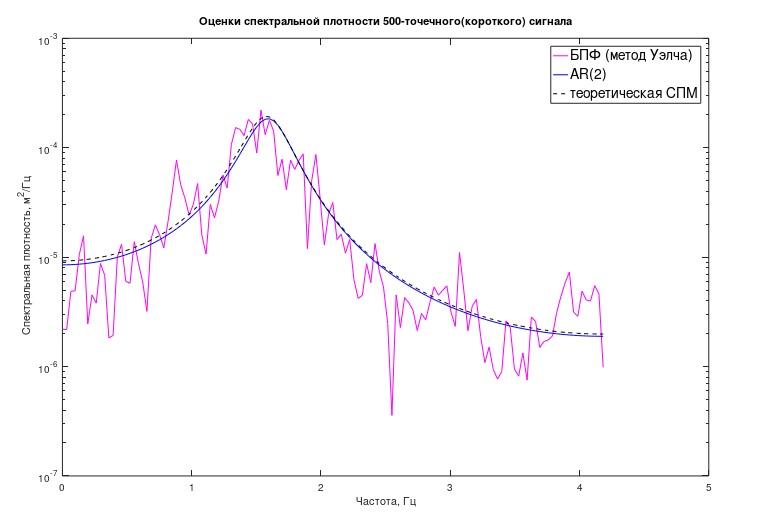Fig. 3 Évaluation classique et autorégressive du processus «court» PSD

De la même manière, selon une expression similaire à (5), le calendrier «théorique» du PSD a été construit plus tôt, seuls les coefficients du modèle y étaient, bien sûr, pris différemment (de (2)).
On peut voir sur le graphique que l'estimation AR de la PSD s'est avérée très proche de celle théoriquement attendue. En plus du graphique, il est possible d'essayer d'évaluer certaines caractéristiques analytiques du processus et du système mécanique associé. Dans ce cas, ce sont les "pôles" du modèle, caractérisant numériquement les fréquences des pics "résonants" du modèle et les "facteurs de qualité" associés.

A partir de (5) nous trouvons la relation pour rechercher les discontinuités de la fonction de transfert de notre modèle en utilisant la transformée de Laplace (en remplaçant jω par λ = -ε + jω):



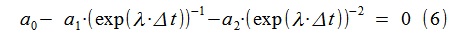
Pour le modèle AR obtenu, λ _1,2 = -1,5427 ± j · 10,1514 a été calculé de cette manière, ce qui est très proche du modèle original utilisé pour générer le processus
λ _1,2theor = -1,2500 ± j · 9,9216 (c'est-à-dire les positions du pic de résonance, respectivement, 1,615 Hz (en théorie) et 1,579 Hz (déterminé)).


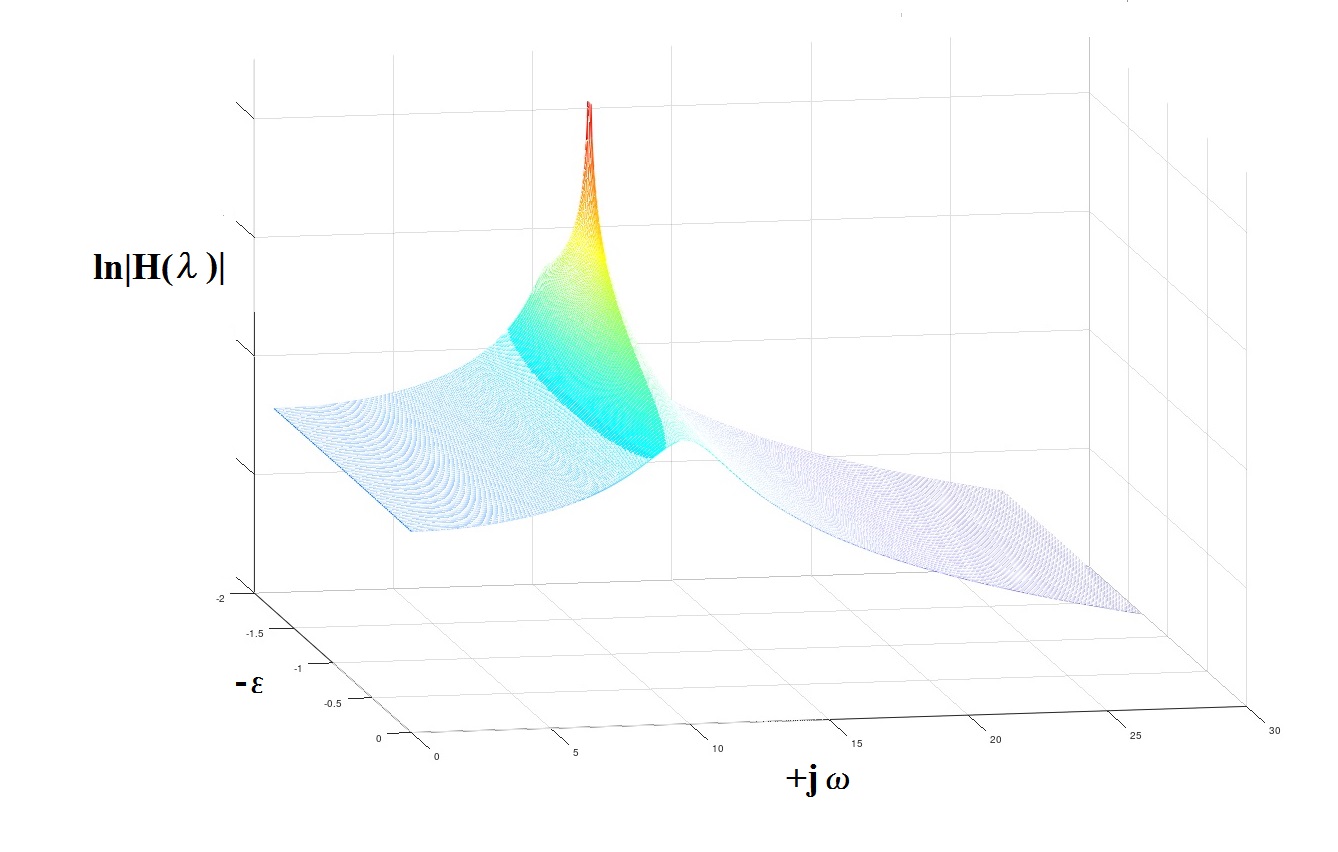Fig. 4 A propos du concept de "pôles"

Quelques commentaires et recommandations en conclusion.

1. L'ordre «excessif» (trop grand) du modèle AR est généralement beaucoup moins dangereux qu'insuffisant, du point de vue du risque d'obtenir une estimation PSD avec des erreurs grossières.
2. En règle générale, la modélisation AR permet de déterminer assez précisément les fréquences de résonance jω _k et beaucoup moins précisément de déterminer les largeurs des «pics» correspondants -ε _k
3. ARMA - le modèle peut s'avérer être beaucoup plus petit (taille) que le modèle AR, qui semble viser à améliorer la précision du modèle, selon de nombreuses sources. Cependant, l'évaluation de la partie MA du modèle est beaucoup plus difficile et peut généralement comprendre la première étape pour obtenir un modèle AR de grand ordre afin de le transformer davantage en partie MA. En relation avec ces sources, une opinion alternative est également exprimée sur l'opportunité d'utiliser exactement des modèles AR pour l'estimation spectrale, bien que d'un ordre supérieur.
4. Pour les processus très courts, ainsi que pour les processus non stationnaires, au lieu de la matrice d'estimations de la fonction d'autocorrélation, la matrice de covariance est généralement utilisée dans (3).
5. Pour une étude détaillée de la question de l'estimation spectrale autorégressive, S.L. Marple ml. «Analyse spectrale numérique et ses applications», M., Mir, 1990