
Dans la communauté scientifique, la visualisation des données et la conception de la théorie jouent un rôle très important. Les outils qui implémentent les commandes LaTeX , tels que Markdown et MathJax, sont souvent utilisés pour une présentation pratique et belle des formules.
Pour Julia, il existe également un ensemble de packages qui vous permettent d'utiliser la syntaxe de LaTeX , et en conjonction avec les moyens de l'algèbre symbolique, nous obtenons un outil puissant pour gérer les formules.
Téléchargez et connectez tout ce dont vous avez besoin pour aujourd'hui
using Pkg Pkg.add("Latexify") Pkg.add("LaTeXStrings") Pkg.add("SymEngine") using Latexify, LaTeXStrings, Plots, SymEngine
LaTeXStrings
LaTeXStrings est un petit package qui facilite la saisie d'équations LaTeX dans les littéraux de chaîne Julia. Lorsque vous utilisez des chaînes régulières dans Julia pour entrer un littéral de chaîne avec des équations LaTeX intégrées, vous devez éviter manuellement toutes les barres obliques inverses et les signes dollar: par exemple, $ \alpha^2 $ est écrit \$\\alpha^2\$ . De plus, bien que IJulia soit capable d'afficher des équations au format LaTeX (via MathJax ), cela ne fonctionnera pas avec les lignes régulières. Par conséquent, le package LaTeXStrings définit:
- La classe
LaTeXString (un sous-type de String ) qui fonctionne comme une chaîne (pour l'indexation, la conversion, etc.), mais s'affiche automatiquement sous forme de texte / latex dans IJulia. - Macros de chaîne
L"..." et L"""...""" qui vous permettent de saisir des équations LaTeX sans s'échapper des barres obliques inverses et des signes dollar (et qui vous ajoutent des signes dollar si vous les omettez).
S = L"1 + \alpha^2"
Le REPL affichera :
"\$1 + \\alpha^2\$"
et Jupyter affichera:
1+ alpha2
L'indexation fonctionne comme des lignes normales:
S[4:7] "+ \\a"
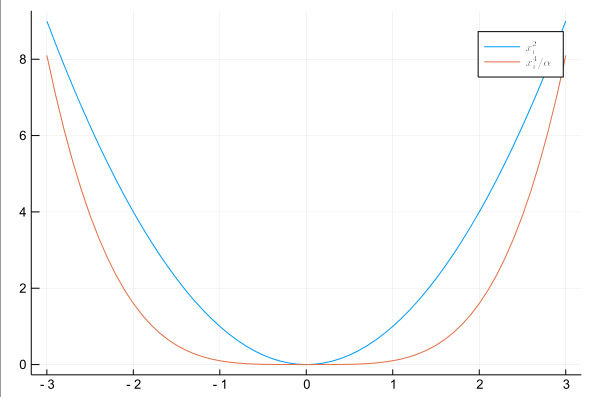
Ces lignes peuvent être utiles dans la conception de graphiques.
x = [-3:0.1:3...] y1 = x .^2 α = 10 y2 = x .^4 / α; plot(x,y1, lab = "\$x^2_i\$") plot!(x,y2, lab = L"x^4_i/\alpha")
Latexify
Un package plus fonctionnel est Latexify ( Guide ). Il est conçu pour générer des mathématiques LaTeX à partir d'objets Julia. Ce package utilise l'homologie de Julia pour convertir des expressions en chaînes au format LaTeX. Latexify.jl fournit des fonctions pour convertir un certain nombre d'objets Julia différents, notamment:
- Expressions
- Cordes
- Numéros (y compris rationnels et complexes),
- Expressions symboliques de SymEngine.jl,
- ParameterizedFunctions et ReactionNetworks de DifferentialEquations.jl
ainsi que des tableaux de tous les types pris en charge.
ex = :(x/(y+x)^2)
fracx gauche(y+x droite)2
str = "x/(2*k_1+x^2)"
fracx2 cdotk1+x2
Tableau d'éléments hétérogènes:
m = [2//3 "e^(-c*t)" 1+3im; :(x/(x+k_1)) "gamma(n)" :(log10(x))] latexify(m)
\ left [\ begin {array} {ccc} \ frac {2} {3} & e ^ {- c \ cdot t} & 1 + 3 \ textit {i} \\ \ frac {x} {x + k_ {1}} & \ Gamma \ left (n \ right) & \ log_ {10} \ left (x \ right) \\ \ end {array} \ right]
\ left [\ begin {array} {ccc} \ frac {2} {3} & e ^ {- c \ cdot t} & 1 + 3 \ textit {i} \\ \ frac {x} {x + k_ {1}} & \ Gamma \ left (n \ right) & \ log_ {10} \ left (x \ right) \\ \ end {array} \ right]
Vous pouvez spécifier une fonction qui affiche les formules et les copie dans le tampon sous la forme compréhensible pour Habr:
function habr(formula) l = latexify(formula) res = "\$\$display\$$l\$display\$\$\n" clipboard(res) return l end habr(ex)
fracx gauche(y+x droite)2
<p>$<!-- math>$$display$$\frac{x}{\left( y + x \right)^{2}}$$display$$</math -->$</p>
Gardez à l'esprit
latexify("x/y") |> display
fracxy
latexify("x/y") |> print
$\frac{x}{y}$
Symengine
SymEngine est un package qui fournit des calculs symboliques que vous pouvez visualiser dans votre Jupyter avec Latexify.
Vous pouvez spécifier des caractères dans les lignes et les guillemets ( quote ):
julia> a=symbols(:a); b=symbols(:b) b julia> a,b = symbols("ab") (a, b) julia> @vars ab (a, b)
Définissez la matrice et affichez-la magnifiquement
u = [symbols("u_$i$j") for i in 1:3, j in 1:3] 3×3 Array{Basic,2}: u_11 u_12 u_13 u_21 u_22 u_23 u_31 u_32 u_33 u |> habr
\ left [\ begin {array} {ccc} u_ {11} & u_ {12} & u_ {13} \\ u_ {21} & u_ {22} & u_ {23} \\ u_ {31} & u_ {32} & u_ {33} \\ \ end {array} \ right]
\ left [\ begin {array} {ccc} u_ {11} & u_ {12} & u_ {13} \\ u_ {21} & u_ {22} & u_ {23} \\ u_ {31} & u_ {32} & u_ {33} \\ \ end {array} \ right]
Supposons que nous ayons des vecteurs
C = symbols("Ω_b/Ω_l") J = [symbols("J_$i") for i in ['x','y','z'] ] h = [0, 0, symbols("h_z")] 3-element Array{Basic,1}: 0 0 h_z
qui doit être multipliée par vecteur
using LinearAlgebra × = cross latexify(J×h, transpose = true)
$$ afficher $$ \ commencer {équation} \ gauche [\ commencer {tableau} {c} J_ {y} \ cdot h_ {z} \\ - J_ {x} \ cdot h_ {z} \\ 0 \\ \ end {array} \ right] \ end {equation} $$ display $$
Calculs matriciels complets:
dJ = C*(u*J.^3)×h latexify( dJ, transpose = true) habr(ans)
$$ afficher $$ \ begin {equation} \ left [\ begin {array} {c} \ frac {h_ {z} \ cdot \ left (u_ {21} \ cdot J_ {x} ^ {3} + u_ { 22} \ cdot J_ {y} ^ {3} + u_ {23} \ cdot J_ {z} ^ {3} \ droite) \ cdot \ Omega_ {b}} {\ Omega_ {l}} \\ \ frac { - h_ {z} \ cdot \ left (u_ {11} \ cdot J_ {x} ^ {3} + u_ {12} \ cdot J_ {y} ^ {3} + u_ {13} \ cdot J_ {z} ^ {3} \ droite) \ cdot \ Omega_ {b}} {\ Omega_ {l}} \\ 0 \\ \ end {array} \ right] \ end {equation} $$ display $$
mais avec une chaîne aussi simple, vous pouvez trouver le déterminant et l'envoyer à Habr
u |> det |> habr
u11 cdot left(u22− fracu12 cdotu21u11 right) cdot left(u33− fracu13 cdotu31u11− frac left(u23− fracu13 cdotu21u11 droite) cdot gauche(u32− fracu12 cdotu31u11 droite)u22− fracu12 cdotu21u11 right)
Récursif! La matrice inverse est probablement calculée de manière similaire:
u^-1 |> habr
Spoiler$$ afficher $$ \ left [\ begin {array} {ccc} \ frac {1 - \ frac {u_ {12} \ cdot \ left (\ frac {- u_ {21}} {u_ {11}} - \ frac {\ left (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31 }} {u_ {11}} \ droite)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) } \ droite) \ cdot \ gauche (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ droite)} {u_ {33} - \ frac {u_ {13 } \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ { 21}} {u_ {11}}}} à droite)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} - \ frac {u_ {13} \ cdot \ left (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31 }} {u_ {11}} \ droite)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) } \ droite)} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u _ {12} \ cdot u_ {31}} {u_ {11}} \ droite)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}}}} {u_ {11}} & \ frac {\ frac {- u_ {12} \ cdot \ left (1 + \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {\ left (u_ {22 } - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} { u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ droite)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} } \ droite)} \ droite)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} + \ frac {u_ {13} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {\ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21} } {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23 } - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} { u_ {11}} \ droite)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ rig ht)}} {u_ {11}} & \ frac {\ frac {- u_ {13}} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12 } \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}} + \ frac { u_ {12} \ cdot \ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {\ left (u_ {22} - \ frac { u_ {12} \ cdot u_ {21}} {u_ {11}} \ droite) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ { 12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right)} } {u_ {11}} \\ \ frac {\ frac {- u_ {21}} {u_ {11}} - \ frac {\ left (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right)} \ right) \ cdot \ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ droite)} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ { 12} \ cdot u_ {31}} {u_ {11}} \ droite)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}}} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} & \ frac {1 + \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} { \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right)}} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} & \ frac {- \ left (u_ {23 } - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {\ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} { u_ {11}} \ droite) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac { u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right )} \\ \ frac {\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ droite)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ à droite)}} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} { u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}} & \ frac {- \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ droite)} {\ gauche (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ droite) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21 }} {u_ {11}} \ droite) \ cdot \ gauche (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ droite)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right)} & \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} { u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ c point \ gauche (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ droite)} {u_ {22} - \ frac {u_ {12} \ cdot u_ { 21}} {u_ {11}}} \ droite) ^ {- 1} \\ \ end {array} \ droite] $$ display $$
Si vous voulez blesser Matjax votre navigateur, mettez moins le deuxième degré (le carré de la matrice inverse)
Soit dit en passant, SymEngine considère les dérivés:
dJ[1] |> habr
frachz cdot left(u21 cdotJ3x+u22 cdotJ3y+u23 cdotJ3z àdroite) cdot Omegab Omegal
diff(dJ[1], J[1]) |> habr
frac3 cdotJ2x cdothz cdotu21 cdot Omegab Omegal
Soit dit en passant, Julia peut utiliser non seulement des formules, mais aussi des graphiques de LaTeX 'a. Et si vous avez installé MikTex et déjà téléchargé pgfplots , puis en utilisant l'environnement approprié, vous pouvez vous lier d' amitié avec Julia, qui vous donnera la possibilité de créer des histogrammes, des graphiques en trois dimensions, des erreurs et des reliefs avec des contours, puis de l'intégrer dans le document LaTeX.
C'est tout avec des formules, mais pas avec des calculs symboliques: Julia a toujours des solutions plus complexes et intéressantes pour l'algèbre symbolique, que nous allons certainement traiter la prochaine fois.