À propos de la proximité des sommets

«Avant de comprendre cela, cela semble être un miracle. Mais après cela, il n'y a plus rien de spécial. »

Non, pas sur les montagnes, sur les comptes. En mathématiques, il y a des questions dont la formulation est accessible à tous, mais la solution n'est pas triviale et sans préparation particulière est difficile à expliquer. Un de ces problèmes peut être brièvement exprimé comme suit: comment calculer correctement les distances dans les graphiques dirigés? Ce problème quelque peu abstrait peut être réduit à une tâche de motivation très spécifique. Il tient dans une seule image:

1. Énoncé du problème. Je vis de l'un, mais toi de l'autre.

Une petite ville est divisée (par exemple, par une rivière, bien que dans le contexte des sommets, la gorge soit plus appropriée) en deux quartiers (parties) $$$A$ et $$$B$ . La communication entre les quartiers s'effectue par une seule route (pont) à deux voies: sur le côté de $$$A$ à $$$B$ et vice versa. Dans le cadre de la croissance démographique, la question s'est posée d'augmenter la capacité de la route. L'argent comme d'habitude est à peine suffisant et suffisant pour une seule voie dans une seule direction. Il est clair que même une voie rapprochera les régions, mais la question est de savoir combien exactement? Vous êtes un mathématicien fou urbain, et c'est vous qui avez été invité afin de recevoir une réponse raisonnable .

À quel point les zones sont-elles plus proches si vous construisez une autre bande dans une direction?

Libellé pour avancé

Au lieu des ponts de Konigsberg , un langage de théorie des graphes légèrement plus rigoureux peut être utilisé. Donc, il y a un graphe orienté avec deux sommets (nœuds) $$$A$ et $$$B$ . L'amplitude de la connexion (conductivité, bande passante) dans le sens direct et inverse est initialement égale. La question est de savoir dans quelle mesure la distance entre les nœuds changera si la conductivité dans l'une des directions est doublée?

Et oui, si vous êtes un vrai soudeur mathématicien, vous pouvez proposer (et justifier) ​​une solution pour toutes les valeurs directes et de rétroaction. Idéalement, pour un graphique avec un nombre quelconque de nœuds et de liens.

Intimité et errances ivres

Il est clair que la distance habituelle (kilométrique) entre les régions ne dépend pas de la présence ou de l'absence de la route. Par conséquent, cela ne convient pas ici - nous devons compter sur la communication. Plus les districts sont connectés - plus ils sont proches - plus les résidents peuvent se rendre dans une autre zone par unité de temps.

Pour évaluer la mesure de proximité entre les nœuds d'un graphe non orienté, la distance dite résistive peut être utilisée. Plus tôt, nous avons déjà décrit les propriétés de cette distance sur le habr dans plusieurs articles .

La distance résistive est équivalente au concept de résistance efficace, lorsqu'il s'agit du réseau électrique. Par conséquent, en langage électrique, le problème peut être formulé comme suit. Entre deux nœuds, deux diodes de conductivités égales sont connectées dans le sens antihoraire. Comment la résistance entre ces points changera-t-elle si vous ajoutez une autre diode? (Je m'excuse si le langage électrique a échoué et j'ai écrit des bêtises ici).

En outre, une résistance efficace peut être interprétée dans le langage de Markov pour les probabilités de promenades aléatoires ivres (pour ceux qui souhaitent se plonger dans le sujet - google "Random Random and réseaux électriques").

La distance résistive est quadratique, - correspond au carré de la distance linéaire. Les distances quadratiques sont également appelées quadrans . Mais comme d'autres distances (linéaires) ne sont pas utilisées dans ce problème, nous n'avons pas besoin du terme quadrans ici. (Il y a suffisamment de langue d'oiseau même sans).

En général, le terme "distance résistive" ne semble pas bon non plus. Il implique que nous parlons d'une sorte de distance inhabituelle inconnue de la science. En fait, la distance résistive est la distance euclidienne habituelle. Mais dans l'espace affine. Nous en utilisons davantage cette fonctionnalité.

Et quel est en fait le problème?

Si nous savons ce qu'est une "distance résistive", alors pourquoi ne pouvons-nous pas "simplement la prendre et la calculer" pour un graphique donné?

Hm. En principe, c'est facile. Si nous parlons d'un graphe non orienté. Si la ville avait construit des bandes dans les deux sens, la distance résistive aurait diminué exactement de moitié. Puisque la résistance est inversement proportionnelle à la conductivité, et la conductivité (débit) a doublé. Et si j'ajoutais deux bandes dans chaque direction, la distance diminuerait de 3 fois. Tout est assez banal ici. (Et probablement, quelqu'un ici peut déjà deviner la forme générale de la solution. Et nous allons plus loin).

Lorsque les relations opposées ne sont pas égales, alors tout se complique. Et assez sévèrement.

Il n'y a pas de moyen juridique généralement accepté pour déterminer la proximité de pics (distances résistives) dans un graphique directionnel .

(Ceci est ma thèse - peut-être que quelqu'un peut me convaincre). «Non» - cela signifie ici que ce n'est pas dans les manuels, le wiki et dans les têtes (plus précisément - il existe de nombreuses façons différentes de différents auteurs qui nécessitent différentes hypothèses et définitions). Il y a un moyen (mais pas si simple). Dans cet article, nous ne faisons que le décrire.

La détermination même de la distance en présence de connexions dirigées nécessite une clarification si l'on parle d'un graphe orienté (métrique non commutative, je m'excuse). Vous pouvez parler de la distance de $$$A$ avant $$$B$ , mais vous pouvez $$$B$ avant $$$A$ . Et très probablement, ces distances ne sont pas toujours égales. De quels types de distances parlons-nous dans le problème?

Règles de distance euclidienne

Nous émergerons et prendrons une profonde respiration. Nous avons déjà mentionné que la distance résistive est l'euclidienne habituelle. Cela signifie que sa définition peut être réduite à la définition de la distance euclidienne comme norme de la différence de deux éléments:

$$$S (A, B) = | A - B | ^ 2 = (A - B) ^ 2 = (A - B) \ cdot (A - B) = S (B, A) \ quad (1)$

Cette définition ne dépend pas de l'ordre des éléments - c'est la distance commutative, la proximité (plus précisément, la distance) des éléments. Un point dans une expression signifie une opération de produit scalaire (espace métrique). En conséquence, l'expression (1) peut être divulguée:

$$$S (A, B) = S (B, A) = A ^ 2 + B ^ 2 - A \ cdot B - B \ cdot A \ quad (2)$

Ici $$$A ^ 2 = A \ cdot A$ , $$$B ^ 2 = B \ cdot B$ - normes d'éléments. En ce qui concerne les graphiques, les normes des éléments sont généralement nulles. Dans le problème d'origine, rien n'est dit sur les normes, vous pouvez donc les prendre à zéro (plus sur ce que signifient les normes des éléments dans l'espace affine. Ici , et encore plus de détails, ici ). L'expression de la distance souhaitée prend alors la forme:

$$$S (A, B) = - (A \ cdot B + B \ cdot A) = s_ {AB} + s_ {BA} \ quad (3)$

Selon l'expression (3), tout ce qui est nécessaire pour résoudre le problème est de trouver les produits scalaires des éléments (nœuds) dans un graphe orienté (c'est facile à dire, mais comment faire?).

En cours de route, la formule (3) montre que notre mesure générale (commutative) de proximité entre les éléments $$$A$ et $$$B$ est la somme de deux distances dirigées:

$$$s_ {AB} = - A \ cdot B$ - distance directionnelle de $$$A$ avant $$$B$ ,
$$$s_ {BA} = - B \ cdot A$ - distance directionnelle de $$$B$ avant $$$A$ .

2. La décision. Longue route dans les dunes

Le grondement s'apaisa. Le plaisir est terminé. Viennent ensuite les détails ternes de la description de l'essence de la méthode de calcul du produit scalaire entre les nœuds d'un graphe orienté. C'est la partie que je ne sais pas dire "de façon simple sur les doigts". Mais c'est là que la chose la plus importante dans l'article. Quelque chose qui mérite de perdre du temps.

Le raisonnement général est le suivant. Nous transférons soigneusement et sans émotions de nouvelles hypothèses supplémentaires les propriétés connues de la métrique des espaces symétriques aux espaces asymétriques. Il suffit de prendre en compte les particularités de la métrique dans les espaces affines.

Tout graphe connecté (orienté ou non) définit un espace métrique affine. Certaines propriétés de ces espaces dans l'exécution symétrique (commutative) ont été décrites (chaotiquement) dans la série d'articles déjà mentionnée ou plus précisément et en détail dans le longrid mentionné. Ne vous précipitez pas pour basculer - ci-dessous, nous donnons (bien que, par la langue tordue) les principales pressions.

Espace métrique affine (graphique non orienté)

Ce qui est important. Bien connu d'abord.

1. L'affinité de l'espace signifie que les concepts de vecteur et d'élément dans l'espace sont différents. Le vecteur est la différence des éléments. Cette caractéristique apparemment insignifiante entraîne des conséquences importantes si une métrique est définie dans l'espace.

2. L'espace est défini par une base composée d'éléments. Les sommets du graphique sont la base de l'espace. Les relations dans un graphique déterminent ses propriétés métriques.

3. Une caractéristique de connectivité du graphe est la matrice d'adjacence . Mais pour les propriétés métriques (et autres), le laplacien du graphique (matrice de Kirchhoff) est plus important $$$L$ .

4. Le laplacien d'un graphe est un tenseur presque métrique. «Presque» - signifie ici qu'il est incomplet. Le laplacien est une matrice dégénérée et donc non inversible. Et le tenseur métrique standard est complètement réversible.

Maintenant moins connu.

5. La différence entre les éléments et les vecteurs dans un espace affine métrique conduit à l'existence d'un vecteur nul en lui $$$\ mathbb z$ . Le produit scalaire des éléments avec un vecteur nul dans un espace commutatif (symétrique) est égal à l'unité (dans un espace non commutatif, cela dépend de la direction de la multiplication). Sans vecteur zéro, l'espace graphique n'est pas complet! C'est important.

6. Le centre orthogonal de la base est double par rapport au vecteur nul. $$$Z$ . Il s'agit d'un élément orthogonal à tous les autres éléments de la base (à l'exception du vecteur zéro). Rappelons que l'orthogonalité des éléments signifie que leur produit scalaire est nul. L'orthocentre d'un triangle est le cercle circonscrit . Oui, dans un espace affine complet, un élément avec une norme non nulle n'est pas un point, mais une sphère à n dimensions.

7. Le laplacien du graphique, ainsi que les coordonnées du centre orthogonal, devient complet (un tenseur métrique à part entière). En d'autres termes, laplacien complet $$$Lm$ Est un laplacien ordinaire $$$L$ mais bordé par les coordonnées barycentriques du centre orthogonal.

8. L'inversion du laplacien complet permet d'obtenir un Gramian complet $$$Gm$ - la matrice des produits scalaires des éléments de la base (dans notre cas, les sommets du graphe). Ce gramian est également un tenseur métrique à part entière de l'espace.

9. Le cadrage d'un gramme complet est un tuple d'unités (produits scalaires des éléments de base et un vecteur zéro). Dans le coin - zéro, c'est la norme du vecteur zéro lui-même.
La fameuse matrice Cayley-Menger est un Gramian presque régulier.

En conséquence, nous concluons que, selon la revendication 8, le problème de la détermination des produits scalaires (et, par conséquent, des distances) entre les nœuds du graphique est réduit à la détermination du tenseur métrique initial de la base $$$Gm$ .

Nous avons besoin d'une méthode pour construire un graphe gramme complet $$$Gm$ pour un laplacien donné (incomplet) $$$L$ .

Dans le cas des liaisons symétriques, la construction d'un Gramian complet à partir du laplacien (et vice versa) ne pose pas de difficultés particulières. Dans ce cas, les produits scalaires des éléments de la base et du vecteur zéro sont commutatifs - ils ne dépendent pas de l'ordre de multiplication:

$$$\ mathbb z \ cdot A = A \ cdot \ mathbb z = 1$

Pour les graphes dirigés (espaces non commutatifs) le problème est compliqué. Ne serait-ce que parce que le nombre même de connexions possibles dans le graphe orienté double.

Espace affine non commutatif (graphique orienté)

À propos des propriétés du laplacien du graphe orienté, nous avons également déjà écrit sur le Habr . Ils ont expliqué comment utiliser les potentiels du Laplacien pour classer les objets. En termes de bases, les potentiels du Laplacien sont les coordonnées duales du vecteur zéro (annihilateur du Laplacien).

Dans cet article, nous nous intéressons aux propriétés métriques. Si le graphique est dirigé, le produit scalaire entre ses sommets dépend de l'ordre:

$$$A \ cdot B \ ne B \ cdot A$

Cela signifie que les doubles coordonnées dans les graphiques dirigés sont divisées (en gauche et en droite). Les valeurs des produits scalaires du vecteur zéro et des éléments de la base (en bordure du gramme) dépendent également de l'ordre des facteurs. Et donc, contrairement à l'espace commutatif, ici la moitié des coordonnées doubles du vecteur zéro est inconnue et doit être déterminée.

$$$\ mathbb z \ cdot A \ ne A \ cdot \ mathbb z$

Cependant, il existe de nombreuses quantités connues.

Tout d'abord, le Laplacien lui-même est connu. De plus, il est connu que la somme de ses lignes est nulle (dans le cas général, c'est une exigence facultative, mais pour les Laplaciens de graphes dirigés c'est généralement le cas). Il est également important que les coordonnées barycentriques des éléments soient uniques, car elles sont indépendantes de la métrique spatiale. Autrement dit, la frontière du laplacien du graphique est symétrique à la fois pour le graphique dirigé et le graphique non dirigé (je n'ai pas immédiatement reconnu ce point). Enfin, nous connaissons les normes des éléments de la base (généralement dans les graphiques elles sont égales à zéro).

Il reste à substituer tout ce qui est connu et inconnu dans l'identité reliant le laplacien et le gramian:

$$$Lm \ Gm = I$

Ici $$$I$ Est une matrice d'identité. Dans cette identité, le sens du passage d'un laplacien incomplet à un complet.

Tais-toi et crois

Passons des mots aux actes. Voici à quoi ressemble le laplacien $$$L$ pour un graphe de deux nœuds:

$$$L = \ begin {bmatrix} c_1 & -c_1 \\ c_2 & -c_2 \ end {bmatrix}$

Pour simplifier, nous avons désigné la relation avec les nombres: $$$c_1 = c_ {AB}, c_2 = c_ {BA}$ . On suppose que les valeurs des liaisons sont connues - à travers elles, nous exprimerons toutes les autres quantités.

Laplacien complet $$$Lm$ comprend les coordonnées de l'orthocentre $$$[rz, az, bz]$ :

$$$Lm = \ begin {bmatrix} rz & az & bz \\ az & c_1 & -c_1 \\ bz & c_2 & -c_2 \ end {bmatrix}$

Ici $$$rz$ - la norme de l'orthocentre (dans le cas symétrique est interprétée comme le carré du rayon), $$$az$ et $$$bz$ - coefficients de décomposition de l'orthocentre sur la base $$$A, B$ (poids barycentriques).

Gramian complet $$$Gm$ Cela ressemble à ceci:

$$$Gm = \ begin {bmatrix} 0 & za & zb \\ 1 & 0 & g_1 \\ 1 & g_2 & 0 \ end {bmatrix}$

Voici les tuples $$$[za, zb]$ et $$$[1, 1]$ reflètent les coordonnées doubles du vecteur nul. Ces coordonnées sont des annihilateurs du laplacien (multipliées par le laplacien, elles donnent un vecteur zéro - à ne pas confondre avec un vecteur zéro!).

Pour résoudre le problème, nous devons trouver la somme des valeurs du gramme: $$$- (g_1 + g_2)$ .

Nous considérons le nombre d'inconnues: $$$rz, az, bz, za, zb, g_1, g_2$ - seulement 7 (oui, oui - pour connaître la valeur d'une distance malheureuse, nous devons calculer sept autres valeurs supplémentaires). Il y a deux connexions bien connues à l'entrée - $$$c_1$ et $$$c_2$ . Identité $$$Lm \ Gm = I$ donnera 9 équations. Total 7 + 2 = 9, - tout converge (étonnamment). Reste à résoudre simplement le système d'équations.

Pour un graphe de deux nœuds, la solution (toutes inconnues) peut être exprimée sous forme explicite. Nous donnons des expressions finies pour les quantités qui nous intéressent. Nous introduisons le concept de connectivité géométrique générale - c'est l'inverse de la norme du centre orthogonal $$$gc = 1 / rz$ . Sa dimension coïncide avec la dimension des liens du graphique. Pour un graphe de deux nœuds (et deux connexions), la connexion géométrique a une belle expression:

$$$gc = 1 / rz = (\ sqrt {c_1} + \ sqrt {c_2}) ^ 2$

Grâce à cette connexion, on peut exprimer des produits scalaires de nœuds:

$$$g_1 = -gc \ sqrt {c_2}, \ quad g_2 = -gc \ sqrt {c_1}$

Vous pouvez traduire des produits scalaires $$$g$ dans les distances directionnelles $$$s$ (3):

$$$s_ {BA} = gc \ sqrt {c_ {AB}}; \ quad s_ {BA} = gc \ sqrt {c_ {AB}}$

La distance commutative souhaitée entre les nœuds est déterminée par la somme:

$$$S (A, B) = s_ {BA} + s_ {AB} = 1 / \ sqrt {c_ {AB} c_ {BA}} \ quad (4)$

Grand-mère est arrivée

Enfin. Expression (4) - c'est la formule souhaitée.

La distance entre les sommets du graphe de deux nœuds est inversement proportionnelle à la racine carrée du produit des contre-liens.

Vous pouvez charger le manuel de l'école avec une autre formule inutile.

Si les connexions sont égales, le résultat coïncide avec la distance résistive dans les graphiques non orientés:

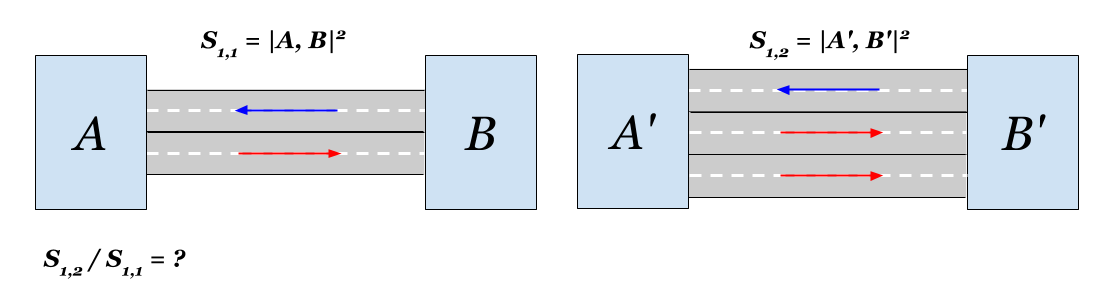
$$$S_ {c, c} (A, B) = 1 / c \ quad (4.1)$

Nous calculerons ce qu'il y a dans notre ville. Si vous posez une deuxième voie, la communication dans une direction doublera. En conséquence, la nouvelle distance $$$S_ {1, 2} (A, B)$ peut être exprimée en termes de l'original:

$$$S_ {1, 2} (A, B) = 1 / \ sqrt {2 c_ {AB} c_ {BA}} = 1 / \ sqrt {2} S_ {1, 1} (A, B)$

La distance entre les zones diminuera en $$$\ sqrt {2}$ fois. C'était évident, non?

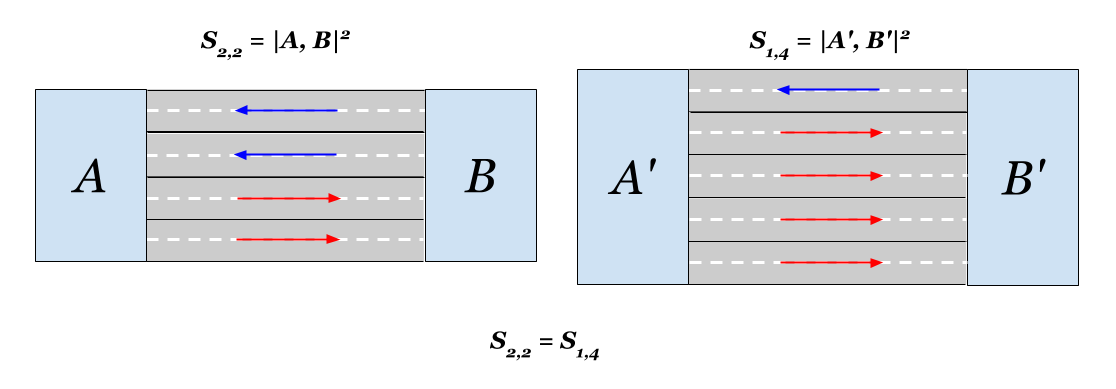
Il s'avère également qu'en termes de distance, l'ajout d'une voie à chaque route à deux voies de chaque côté équivaut à l'ajout de trois voies d'un côté. La proximité euclidienne doublera dans les deux cas. Intéressant.



C’est tout. Merci de votre attention).