En mathématiques, où la preuve est tout, les faits sont également importants. Cependant, les faits sont bons, seulement tant que le modèle est bon et que la construction de modèles est une profession peu fiable. Alors, combien de faits suffiront?

Pouvez-vous trouver le numéro suivant dans la séquence?
1, 2, 4, 8
Voici un numéro de plus si vous avez besoin de plus de données pour prendre une décision:
1, 2, 4, 8, 16
Le prochain numéro devrait être 32, non? Le schéma est clair: pour trouver le numéro suivant, vous devez doubler le précédent. 1 × 2 = 2; 2 × 2 = 4; 4 × 2 = 8; 8 × 2 = 16. Donc, le nombre suivant devrait être 16 × 2 = 32. Combien de faits supplémentaires sont nécessaires pour confirmer cela?
Mais, bien qu'il soit raisonnable de supposer que le nombre suivant est 32, ce ne sera pas toujours vrai. Considérez la séquence suivante: nous compterons le nombre de sections dans lesquelles le cercle est divisé par des lignes reliant les points situés sur un cercle.
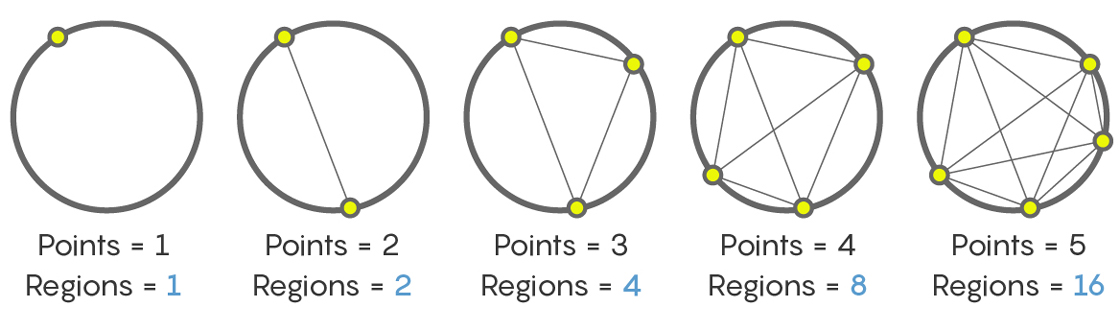
Un point donne une section (toute la partie intérieure du cercle). Deux points - deux sections. Trois points - quatre sections. Cinq et six sont respectivement huit et seize. Le résultat est une séquence
1, 2, 4, 8, 16
Et combien de sections apparaîtront après avoir connecté les lignes de six points sur le cercle? Personne ne vous condamnera si vous, comme beaucoup de personnes confrontées à cette tâche pour la première fois, dites 32. Mais ce n'est pas le cas. En fait, aussi ennuyeux soit-il, la réponse sera - 31! Racontez-vous, puis vérifiez à nouveau.
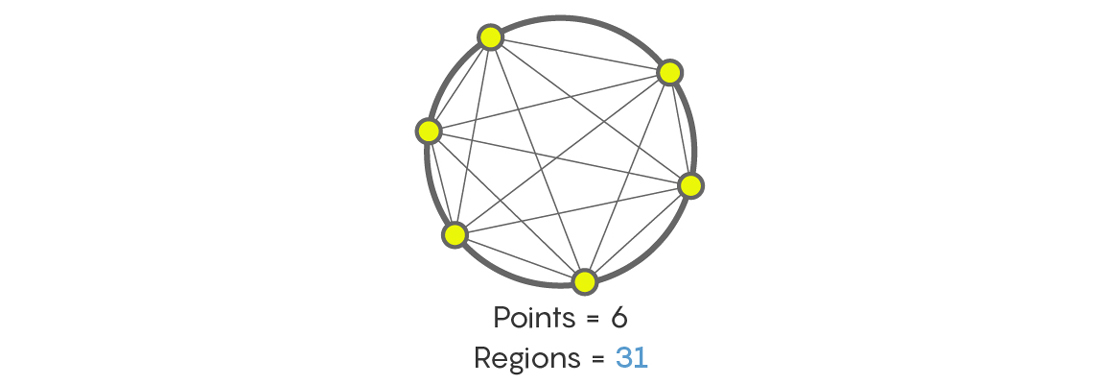
Bien sûr, il existe des séquences comme 1, 2, 4, 8, 16, 32, 64, etc., à partir de doublons de nombres à chaque fois. Mais il existe d'autres séquences, par exemple, le nombre maximal de sections dans lesquelles le cercle est divisé par des lignes reliant les points sur le cercle, à savoir 1, 2, 4, 8, 16, 31, 57, 99, etc. En respectant la séquence 1, 2, 4, 8, 16, nous pourrions penser que tous les faits sont que le prochain numéro sera 32, mais il peut y avoir autre chose.
Les mathématiques ont une longue tradition de défier nos attentes et de faire fonctionner notre imagination. Par conséquent, les mathématiciens s'efforcent toujours d'obtenir des preuves rigoureuses, pas seulement des faits. La preuve établit la vérité mathématique. Tous les faits peuvent indiquer 32 comme le prochain numéro de notre séquence, mais sans preuve rigoureuse, nous ne pouvons en être sûrs.
Mais encore, les faits pour les mathématiciens sont utiles et importants. Avant de prouver quelque chose, nous jouons souvent avec les informations disponibles, étudions le problème, considérons des exemples et collectons des données. Nous étudions et soupesons les faits et décidons quoi faire ensuite. Ces résultats forment notre opinion, proposant de prouver certains théorèmes et de réfuter d'autres.
L'hypothèse du premier principe est un exemple où les faits contrôlent notre pensée mathématique de la même manière que la preuve. Les nombres premiers jumeaux sont des paires de nombres premiers qui diffèrent de 2 - par exemple, 3 et 5, 11 et 13, 101 et 103. L'hypothèse des nombres premiers jumeaux suggère qu'il n'y a pas de plus grande paire de tels jumeaux - c'est-à-dire similaire les paires apparaissent constamment sur la droite numérique lors du passage à l'infini.
L'hypothèse du premier principe n'est pas un théorème, car, bien qu'il s'agisse de l'un des problèmes les plus connus de la théorie des nombres, personne n'a encore été en mesure de le prouver. Cependant, presque tout le monde pense que c'est vrai, car il existe de nombreux faits à l'appui.
Par exemple, dans notre recherche de nombres premiers, nous trouvons constamment de très grandes paires de nombres premiers jumeaux.
Aujourd'hui, chacun des nombres premiers de la plus grande
paire connue contient 400 000 chiffres. Des théorèmes similaires à cette hypothèse sont également démontrés. En 2013,
Zhang Ethan a choqué la communauté mathématique en prouvant la présence d'un nombre infiniment grand de paires de nombres premiers, ne différant pas de plus de 70 millions. Grâce au projet
Polymath ouvert qui a suivi, nous savons qu'il existe un nombre infini de paires de nombres premiers qui ne diffèrent
pas de plus de 246 . Nous n'avons pas encore prouvé l'existence d'un nombre infini de paires de nombres premiers qui diffèrent par 2 - mais 2 est encore beaucoup plus proche de 246 que 246 de l'infini.
Pour ces raisons et d'autres, la croyance en la justice, même si l'hypothèse n'est pas prouvée, n'est pas très controversée. Cependant, il existe d'autres domaines des mathématiques dans lesquels les faits sont utilisés pour construire des opinions éclairées qui se révèlent plus controversées.
Dans l'étude des courbes elliptiques, son rang, grosso modo, dénote une estimation numérique de la complexité de résolution de cette courbe. Pendant de nombreuses années, on a cru que les
rangs des courbes elliptiques n'étaient pas limités , c'est-à-dire qu'il n'y avait aucune restriction sur la valeur du rang de la courbe ou sur la complexité de la solution.
Cependant, des travaux récents amènent les mathématiciens à réfléchir à la possibilité d'un rang limité. L'article donne des faits indiquant qu'il est possible qu'il existe un nombre fini de courbes dont le rang est supérieur à 21.
Cependant, la prudence est recommandée. Les faits collectés par les mathématiciens ne sont pas tirés du monde des courbes elliptiques - ils concernent les matrices que les chercheurs ont utilisées pour modéliser les courbes. Les modèles mathématiques sont largement utilisés en science, et ils peuvent même être tournés vers l'intérieur pour étudier les mathématiques elles-mêmes. Ce sont des outils incroyablement puissants qui nous permettent de remplacer une tâche incompréhensible par une tâche plus facile à gérer pour nous.
Mais l'utilisation de modèles est une entreprise délicate. Vous ne pouvez jamais être sûr que le modèle se comporte de manière assez similaire à ce que nous essayons de comprendre, afin que nous puissions tirer des conclusions de son comportement. De plus, on ne peut pas être sûr que notre modèle soit similaire précisément aux endroits de la plus haute importance. Il est donc difficile de s'assurer que les faits que nous avons collectés sur la base de modèles témoignent réellement des propriétés réelles des phénomènes que nous étudions. Examinons ces problèmes à partir d'un modèle simple d'hypothèse simple.
Imaginez que nous voulons étudier l'énoncé suivant: deux lignes quelconques sont soit intersectées soit parallèles.
Par intersection, nous entendons la présence de lignes droites dans des points communs, et par parallélisme le fait qu'elles vont dans une direction mais ne se coupent pas (ce concept peut être défini d'une autre manière, mais je vais l'utiliser pour plus de simplicité).
Pour étudier ce problème, créez un modèle. Chaque ligne est représentée par l'équation de la ligne oblique, que vous vous souvenez du cours de l'école. Autrement dit, nous supposons que chaque ligne peut être décrite par une équation de la forme
y = mx + b
où m est la pente de la ligne (sa pente) et b est le point d'intersection de l'axe y (axe vertical).
La modélisation des lignes de cette manière est pratique pour les expérimenter dessus. Le modèle nous permet de créer une ligne aléatoire en sélectionnant une paire de nombres aléatoires, m et b. Nous pouvons sélectionner une paire de lignes aléatoires et les vérifier - se croisent-elles? Vont-ils dans un sens? Est-ce qu'il se passe autre chose?
Voici quelques exemples de ce à quoi pourraient ressembler les résultats de telles expériences.
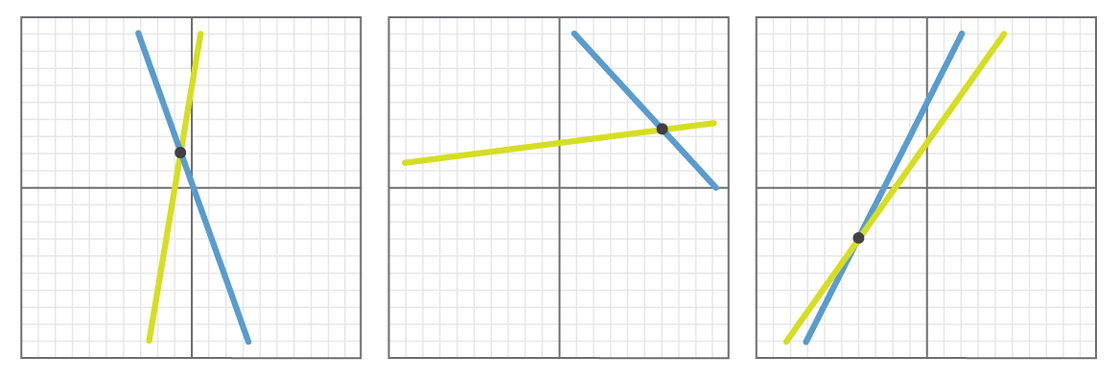
Dans chaque exemple, des lignes sélectionnées au hasard se coupent. Si nous menons cette expérience mille fois - ou 10000, ou un million - nous constaterons que dans tous les cas les lignes se coupent ou sont parallèles (et très probablement, toutes les lignes se coupent, car il est peu probable que les deux lignes aient la même pente, choisie par hasard).
Par conséquent, en regardant un million d'exemples, vous pouvez conclure que l'hypothèse est probablement vraie. Tous les faits corroborent pleinement l'affirmation selon laquelle toute paire de lignes est parallèle ou intersectée.
Cependant, les faits sont aussi bons que le modèle est bon, et la modélisation est dangereuse. Voyons quels dangers nous nous sommes créés dans notre exemple.
Un problème est que certains types de lignes seront plus courants que d'autres. Voici un graphique montrant 50 lignes avec b = 0 et 0 ≤ m ≤ 1.
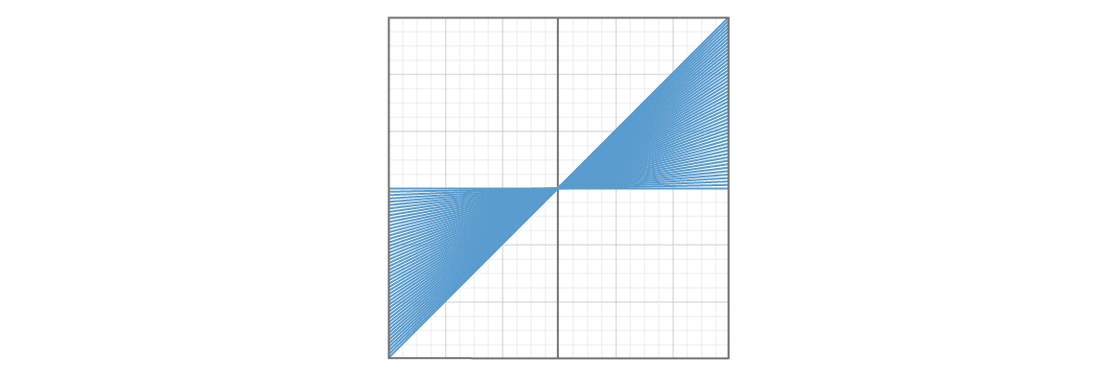
Et voici un graphique montrant 50 lignes avec b = 0 et m ≥ 1.

Il semble qu'un quart de l'avion soit couvert de lignes droites avec une pente de 0 à 1, et un autre quart est couvert de lignes droites avec une pente supérieure à 1. Le choix d'un nombre supérieur à 1 semble plus probable que le choix d'un nombre de 0 à 1, donc la ligne droite est plus probable sera dans la deuxième section de l'avion. Cela signifie que certaines lignes, avec une pente de 0 à 1, seront extrêmement peu représentées dans le modèle. Et si des choses étranges se produisent dans cette partie de l'avion avec des lignes droites, il est peu probable que notre modèle nous en parle.
Si vous regardez attentivement le deuxième graphique, nous verrons un autre problème. Plus m est grand, plus les lignes droites seront raides. La ligne droite la plus fraîche est verticale. Quelle est la pente de la ligne verticale? Par définition, il n'est pas défini: il n'y a pas un tel nombre m qui pourrait décrire la ligne verticale. Il s'avère qu'il n'y a pas de ligne verticale dans notre modèle, et nous ne pouvons pas l'expérimenter. Nous n'avons pas encore commencé à collecter des faits, mais nous avons déjà exclu certains cas particuliers simplement en raison du modèle de construction.
Il en va de même du problème le plus grave de notre modèle. Les gens qui imaginent facilement l'espace tridimensionnel ont probablement remarqué tout de suite que notre hypothèse était fausse. Une ligne droite n'a pas besoin de se croiser ou d'être parallèle. Imaginez deux couloirs allant dans des directions différentes à différents étages d'un bâtiment. Ce sont des lignes droites qui se croisent - des lignes droites qui ne se coupent pas et ne sont pas parallèles.
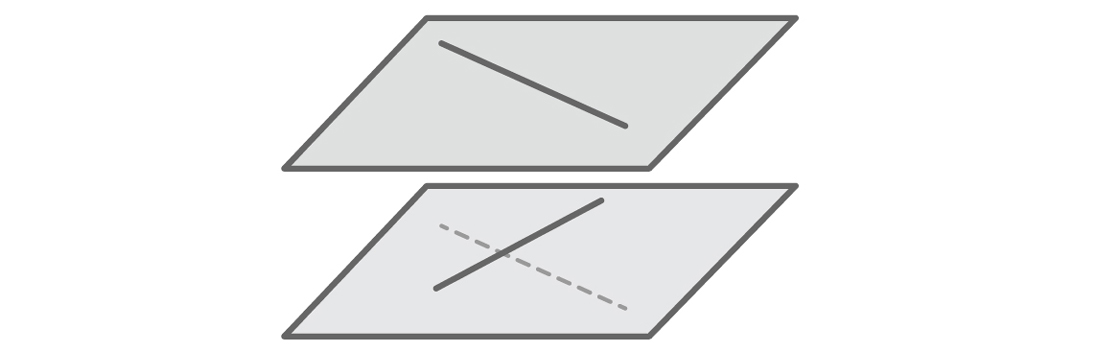
Les lignes transversales doivent se situer dans des plans différents. Mais comme notre modèle définit n'importe quelle ligne via l'équation y = mx + b, nous imaginons automatiquement que toutes les lignes sont dans le même plan. Notre modèle ne donnera que des faits qui soutiennent notre hypothèse, car si deux lignes se trouvent dans le même plan, elles doivent vraiment se croiser ou se paralléliser. Nous ne verrons pas d'autres faits: il n'y a pas de lignes d'intersection dans notre modèle. Comme dans le cas des lignes verticales, le modèle a exclu ce que nous ne pouvions pas imaginer.
Ceci est un exemple simple utilisant un modèle stupide avec un tas de problèmes, y compris des questions délicates, telles que la procédure pour choisir des nombres aléatoires parmi des ensembles infinis. Les mathématiciens professionnels étudiant les rangs des courbes elliptiques n'auraient jamais commis des erreurs aussi simples et évidentes.
Ces mathématiciens savent quelles précautions prendre lorsqu'ils travaillent avec des modèles. Ils savent que, quelle que soit l'utilité et l'intérêt du modèle, ou à quel point les faits collectés seront convaincants, les courbes elliptiques peuvent révéler des propriétés qu'elles n'imaginaient pas. Et si cela ne peut pas être imaginé, votre modèle n'en tiendra pas compte et, par conséquent, les faits ne seront pas reflétés.
Mais que le nouveau modèle soit correct ou non, il a obligé les mathématiciens à penser de manière productive aux courbes elliptiques. Si elle reflète vraiment la vérité, alors les idées du monde des matrices peuvent expliquer le comportement des courbes. Sinon, comprendre pourquoi les courbes elliptiques ne peuvent pas être modélisées de cette manière peut conduire à une meilleure compréhension du problème. Les faits que nous collectons peuvent nous rapprocher de la preuve, d'une manière ou d'une autre.