Liens rapides
-
La route vers la version 12-
Tout d'abord, quelques mathématiques-
Le calcul de l'incertitude-
Mathématiques classiques, élémentaire et avancé-
Plus avec des polygones-
Informatique avec Polyèdres- La
géométrie de style euclide rendue calculable-
Aller super-symbolique avec les théories axiomatiques-
Le problème des n-corps-
Extensions linguistiques et commodités-
Plus de superfonctions d'apprentissage automatique-
Le plus récent des réseaux de neurones-
Calcul avec images-
Reconnaissance vocale et plus avec audio-
Traitement du langage naturel-
Chimie numérique-
Calcul géographique étendu-
Beaucoup de petites améliorations de visualisation-
Resserrement de l'intégration de la base de connaissances-
Intégration du Big Data à partir de bases de données externes-
RDF, SPARQL et tout ça-
Optimisation numérique-
Analyse par éléments finis non linéaire-
Nouveau compilateur sophistiqué-
Appel de Python et d'autres langues-
Plus pour le Wolfram "Super Shell"-
Marionnette d'un navigateur Web-
Microcontrôleurs autonomes-
Appel de la langue Wolfram à partir de Python et d'autres endroits-
Lien avec l'Unity Universe-
Environnements simulés pour l'apprentissage automatique-
Calcul de Blockchain (et CryptoKitty)-
Et la crypto ordinaire aussi-
Connexion aux flux de données financières-
Génie logiciel et mises à jour de plateforme-
Et bien d'autres ...
16 avril 2019 - Stephen Wolfram
Aujourd'hui, nous publions la version 12 de
Wolfram Language (et
Mathematica ) sur
les plates -
formes de bureau et dans
Wolfram Cloud . Nous avons publié la
version 11.0 en août 2016 ,
11.1 en mars 2017 ,
11.2 en septembre 2017 et
11.3 en mars 2018 . C'est un grand saut de la version 11.3 à la version 12.0. Au total, il existe
278 fonctions entièrement nouvelles , dans peut-être 103 domaines, ainsi que des milliers de mises à jour différentes à travers le système:
Dans une «
version entière » comme 12, notre objectif est de fournir de nouveaux domaines de fonctionnalité entièrement remplis. Mais dans chaque version, nous voulons également fournir les derniers résultats de nos efforts de R&D. Dans la version 12.0, peut-être la moitié de nos nouvelles fonctions peuvent être considérées comme des zones de finition qui ont été lancées dans les versions «.1» précédentes - tandis que la moitié commence de nouvelles zones. Je vais discuter des deux types de fonctions dans cette pièce, mais je mettrai particulièrement l'accent sur les spécificités de ce qui est nouveau en passant de 11.3 à 12.0.
Je dois dire que maintenant que 12.0 est terminé, je suis étonné de voir combien il y en a et combien nous avons ajouté depuis 11.3. Dans mon discours lors de notre conférence sur la
technologie Wolfram en octobre dernier, j'ai résumé ce que nous avions jusqu'à présent - et même cela a pris près de 4 heures. Maintenant, il y a encore plus.
Ce que nous avons pu faire est un témoignage à la fois de la force de nos efforts de R&D et de l'efficacité du Wolfram Language en tant qu'environnement de développement. Ces deux choses ont bien sûr été
construites pendant trois décennies . Mais une chose qui est nouvelle avec la version 12.0, c'est que nous avons laissé les gens regarder notre processus de conception en arrière-plan - en
direct sur plus de 300 heures de mes réunions de conception internes . Donc, en plus de tout le reste, je soupçonne que cela fait de la version 12.0 la toute première version logicielle majeure de l'histoire qui a été ouverte de cette manière.
OK, alors quoi de neuf dans 12.0? Il y a des choses grandes et surprenantes - notamment en
chimie , en
géométrie , en
incertitude numérique et en
intégration de bases de données . Mais dans l'ensemble, il y a beaucoup de choses dans de nombreux domaines - et en fait, même le résumé de base d'entre elles dans le
Centre de documentation est déjà de 19 pages:
Bien que de nos jours la grande majorité de ce que fait le Wolfram Language (et Mathematica) ne soit pas ce qui est généralement considéré comme des mathématiques, nous déployons toujours d'immenses efforts de R&D pour repousser les frontières de ce qui peut être fait en mathématiques. Et comme premier exemple de ce que nous avons ajouté dans 12.0, voici le
ComplexPlot3D plutôt coloré:
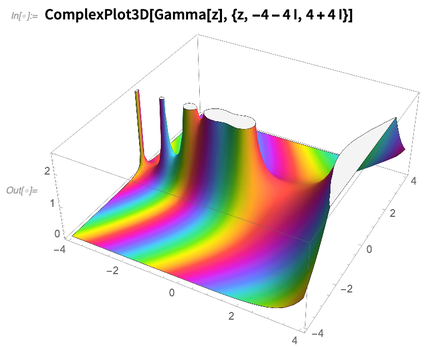
Il a toujours été possible d'écrire du code Wolfram Language pour faire des tracés dans le plan complexe. Mais ce n'est que maintenant que nous avons résolu les problèmes mathématiques et d'algorithmes qui sont nécessaires pour automatiser le processus de traçage robuste de fonctions même assez pathologiques dans le plan complexe.
Il y a des années, je me souviens d'
avoir comploté minutieusement la
fonction du
dilogarithme , avec ses parties réelles et imaginaires. Maintenant,
ReImPlot le fait:
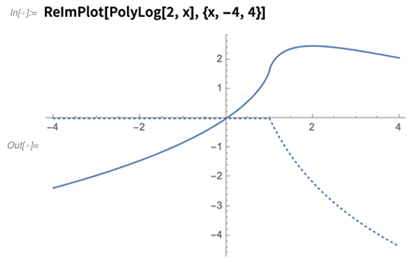
La visualisation de fonctions complexes est (jeu de mots) une histoire complexe, avec des détails qui font une grande différence dans ce que l'on remarque sur une fonction. Et donc l'une des choses que nous avons faites dans 12.0 est d'introduire des moyens standardisés soigneusement sélectionnés (tels que
les fonctions de couleur nommées) pour mettre en évidence différentes fonctionnalités:
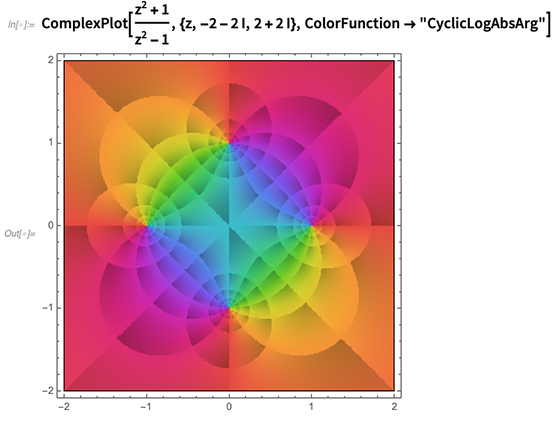
Le calcul de l'incertitude
Les mesures dans le monde réel comportent souvent une incertitude qui est représentée sous forme de valeurs avec ± erreurs. Nous avons des modules complémentaires pour gérer les «nombres avec des erreurs» depuis des lustres. Mais dans la version 12.0, nous construisons des calculs avec incertitude, et nous le faisons correctement.
La clé est l'objet symbolique
Autour de [
x, δ ], qui représente une valeur «autour de
x », avec une incertitude
δ :
Vous pouvez faire de l'arithmétique avec
Around , et il y a tout un calcul pour combiner les incertitudes:
Si vous tracez des nombres
autour , ils seront affichés avec des barres d'erreur:
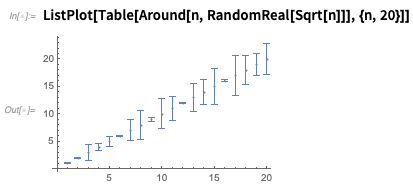
Il existe de nombreuses options - comme voici une façon de montrer l'incertitude à la fois dans
x et
y :
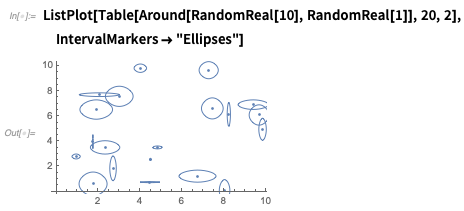
Vous pouvez avoir
environ des quantités:
Et vous pouvez également avoir des objets symboliques
autour :
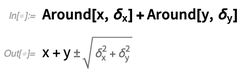
Mais qu'est-ce qu'un objet
Around ? C'est quelque chose où il existe certaines règles pour combiner les incertitudes, qui sont basées sur des distributions normales non corrélées. Mais rien ne dit
qu'Autour [
x, δ ] représente tout ce qui suit réellement en détail une distribution normale - pas plus que cet
Autour [
x, δ ] ne représente un nombre spécifiquement dans l'intervalle défini par
Intervalle [{
x - δ, x + δ }]. C'est juste que les objets
Around propagent leurs erreurs ou incertitudes selon des règles générales cohérentes qui capturent avec succès ce qui est généralement fait en science expérimentale.
OK, alors disons que vous faites un tas de mesures d'une certaine valeur. Vous pouvez obtenir une estimation de la valeur - avec son incertitude - en utilisant
MeanAround (et, oui, si les mesures elles-mêmes ont des incertitudes, celles-ci seront prises en compte dans la pondération de leurs contributions):
Les fonctions partout dans le système - notamment dans
l'apprentissage automatique - commencent à avoir l'option
ComputeUncertainty ->
True , ce qui leur fait donner des objets
Around plutôt que des nombres purs.
Around peut sembler être un concept simple, mais il est plein de subtilités - c'est la principale raison pour laquelle il a fallu jusqu'à présent pour qu'il pénètre dans le système. Beaucoup de subtilités tournent autour des corrélations entre les incertitudes. L'idée de base est que l'incertitude de chaque objet
Around est supposée indépendante. Mais parfois, on a des valeurs avec des incertitudes corrélées - et donc en plus de
Around , il y a aussi
VectorAround , qui représente un vecteur de valeurs potentiellement corrélées avec une matrice de covariance spécifiée.
Il y a encore plus de subtilité lorsqu'il s'agit de choses comme les formules algébriques. Si l'on remplace x ici par un
Around , alors, en suivant les règles de
Around , chaque instance est supposée non corrélée:
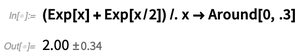
Mais on veut probablement supposer ici que même si la valeur de x peut être incertaine, elle va être la même pour chaque instance, et on peut le faire en utilisant la fonction
AroundReplace (notez que le résultat est différent):
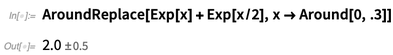
Il y a beaucoup de subtilité dans la façon d'afficher des nombres incertains. Comme le nombre de 0 fin que vous devez mettre:
Ou quelle précision de l'incertitude devez-vous inclure (il y a un point d'arrêt conventionnel lorsque les chiffres de fin sont 35):
Dans de rares cas où beaucoup de chiffres sont connus (pensez, par exemple, à certaines
constantes physiques ), on veut aller d'une manière différente pour spécifier l'incertitude:
Et ça continue encore et encore. Mais progressivement,
Around va commencer à apparaître dans tout le système. Soit dit en passant, il existe de nombreuses autres façons de spécifier des nombres
autour . Il s'agit d'un nombre avec une erreur relative de 10%:
Voici ce que
Around peut faire de mieux pour représenter un intervalle:
Pour une
distribution ,
Around calcule la variance:
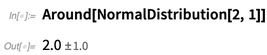
Il peut également prendre en compte l'asymétrie en donnant des incertitudes asymétriques:
Mathématiques classiques, élémentaire et avancé
En faisant du calcul mathématique, il est toujours difficile à la fois de «tout faire correctement» et de ne pas confondre ni intimider les utilisateurs élémentaires. La version 12.0 introduit plusieurs choses pour vous aider. Tout d'abord, essayez de résoudre une
équation quintique irréductible:
Dans le passé, cela aurait montré un tas d'objets
racine explicites. Mais maintenant, les objets
Root sont formatés sous forme de boîtes montrant leurs valeurs numériques approximatives. Les calculs fonctionnent exactement de la même manière, mais l'affichage n'impose pas immédiatement aux gens d'avoir à connaître les nombres algébriques.
Quand nous disons
Intégrer , nous voulons dire «trouver une intégrale», au sens d'antidérivatif. Mais dans le calcul élémentaire, les gens veulent voir des constantes d'intégration explicites (comme ils l'ont toujours dans
Wolfram | Alpha ), nous avons donc ajouté
une option pour cela (et C [
n ] a également une nouvelle forme de sortie agréable):
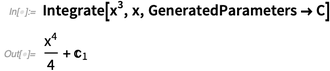
Lorsque nous évaluons nos capacités d'intégration symbolique, nous nous en sortons très bien. Mais il y a toujours plus à faire, en particulier pour trouver les formes d'intégrales les plus simples (et au niveau théorique, c'est une conséquence inévitable de l'indécidabilité de l'équivalence des expressions symboliques). Dans la version 12.0, nous avons continué à repousser les limites, en ajoutant des cas comme:
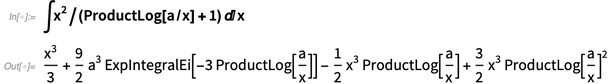
Dans la version 11.3, nous avons introduit l'analyse asymptotique, permettant de trouver des valeurs asymptotiques d'intégrales et ainsi de suite. La version 12.0 ajoute des sommes asymptotiques, des récurrences asymptotiques et des solutions asymptotiques aux équations:
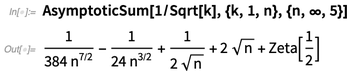
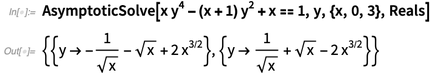
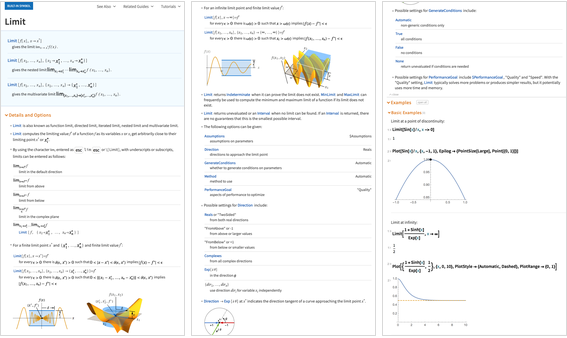
L'une des grandes choses à propos du calcul mathématique est qu'il nous donne de nouvelles façons d'expliquer les mathématiques elles-mêmes. Et quelque chose que nous avons fait est d'améliorer notre documentation afin qu'elle explique les mathématiques ainsi que les fonctions. Par exemple, voici le début de la documentation sur
Limit - avec des diagrammes et des exemples des idées mathématiques de base:
Les polygones font partie du Wolfram Language depuis la version 1. Mais dans la version 12.0, ils se généralisent: il existe désormais un moyen systématique de spécifier des trous. Un cas d'utilisation géographique classique est le polygone pour
l'Afrique du Sud - avec son trou pour le pays du
Lesotho .
Dans la version 12.0, tout comme
Root ,
Polygon obtient une nouvelle forme d'affichage pratique:
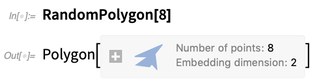
Vous pouvez calculer avec comme avant:
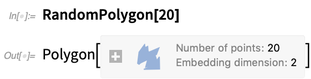
RandomPolygon est également nouveau. Vous pouvez demander, disons, 5 polygones convexes aléatoires, chacun avec 10 sommets, en 3D:
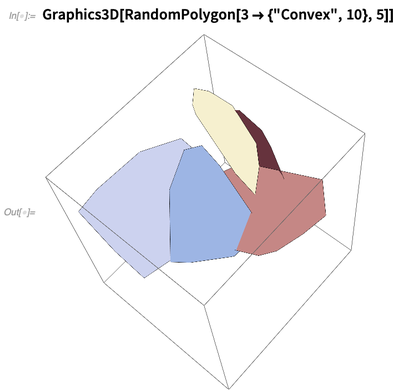
Il y a beaucoup de nouvelles opérations sur les polygones. Comme
PolygonDecomposition , qui peut, par exemple, décomposer un polygone en parties convexes:
Les polygones avec des trous introduisent également un besoin pour d'autres types d'opérations, comme
OuterPolygon ,
SimplePolygonQ et
CanonicalizePolygon .
Les polygones sont assez simples à spécifier: vous donnez simplement leurs sommets dans l'ordre (et s'ils ont des trous, vous donnez également les sommets des trous). Les polyèdres sont un peu plus compliqués: en plus de donner les sommets, il faut dire comment ces sommets forment des faces. Mais dans la version 12.0,
Polyhedron vous permet de le faire dans une généralité considérable, y compris les vides (l'analogue 3D des trous), etc.
Mais d'abord, reconnaissant leurs plus de
2000 ans d'histoire , la version 12.0 introduit des fonctions pour les cinq
solides platoniciens :
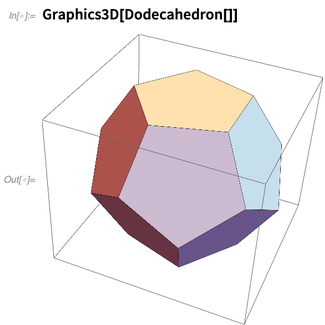
Et étant donné les solides platoniciens, on peut immédiatement commencer à calculer avec eux:
Voici l'angle solide sous-tendu au sommet 1 (car c'est platonique, tous les sommets donnent le même angle):
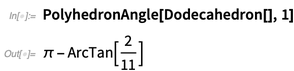
Voici une opération effectuée sur le polyèdre:
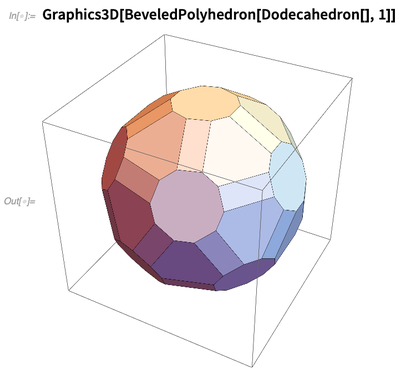
Au-delà des solides platoniciens, la version 12 intègre également tous les «
polyèdres uniformes » (
n bords et
m faces se rencontrent à chaque sommet) - et vous pouvez également obtenir des versions symboliques en
polyèdre des polyèdres nommés de
PolyhedronData :
Vous pouvez créer n'importe quel polyèdre (y compris un «aléatoire», avec
RandomPolyhedron ), puis faire les calculs que vous voulez dessus:
Mathematica et Wolfram Language sont très puissants pour faire à la fois une
géométrie de calcul explicite et une
géométrie représentée en termes d'algèbre . Mais qu'en est-il de la géométrie dans
les éléments d'Euclide - dans laquelle on fait des affirmations géométriques et voit ensuite quelles sont leurs conséquences?
Eh bien, dans la version 12, avec toute la tour de technologie que nous avons construite, nous sommes enfin en mesure de proposer un nouveau style de calcul mathématique - qui automatise en fait ce qu'Euclid faisait il y a plus de 2000 ans. Une idée clé est d'introduire des «scènes géométriques» symboliques qui ont des symboles représentant des constructions telles que des points, puis de définir des objets géométriques et des relations en fonction de ceux-ci.
Par exemple, voici une scène géométrique représentant un triangle
a, b, c et un cercle passant par
a, b et
c , avec le centre
o , avec la contrainte que
o est au milieu de la ligne de
a à
c :
En soi, c'est juste une chose symbolique. Mais nous pouvons faire des opérations dessus. Par exemple, nous pouvons en demander une instance aléatoire, dans laquelle
a, b, c et
o sont rendus spécifiques:
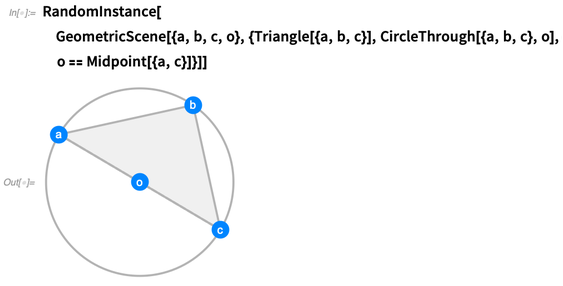
Vous pouvez générer autant d'instances aléatoires que vous le souhaitez. Nous essayons de rendre les instances aussi génériques que possible, sans coïncidences qui ne soient pas forcées par les contraintes:
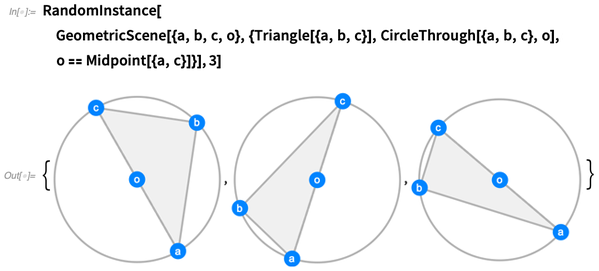
D'accord, mais maintenant, «jouons à Euclide» et trouvons des conjectures géométriques cohérentes avec notre configuration:
Pour une scène géométrique donnée, il peut y avoir de nombreuses conjectures possibles. Nous essayons de sélectionner les plus intéressants. Dans ce cas, nous en arrivons à deux - et ce qui est illustré est le premier: que la ligne ba est perpendiculaire à la ligne cb. En l'occurrence, ce résultat apparaît en fait dans Euclide (il est dans le
livre 3, dans le cadre de la proposition 31 ) - bien qu'il soit généralement appelé
théorème de Thales .
Dans 12.0, nous avons maintenant tout un langage symbolique pour représenter les choses typiques qui apparaissent dans la géométrie de style Euclide. Voici une situation plus complexe - correspondant à ce qu'on appelle
le théorème de Napoléon :
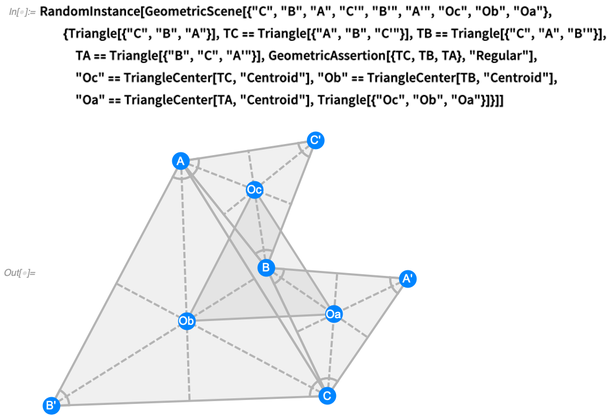
Dans 12.0, il existe de nombreuses fonctions géométriques nouvelles et utiles qui fonctionnent sur des coordonnées explicites:
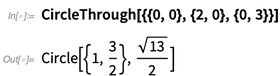
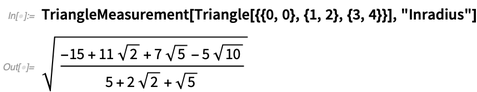
Pour les triangles, 12 types de «centres» sont pris en charge et, oui, il peut y avoir des coordonnées symboliques:
Et pour soutenir la mise en place de déclarations géométriques, nous avons également besoin d '«
assertions géométriques ». Dans 12.0, il existe 29 types différents - tels que
«Parallèle» ,
«Congruent» ,
«Tangent» ,
«Convex» , etc. Voici trois cercles déclarés tangents par paire:
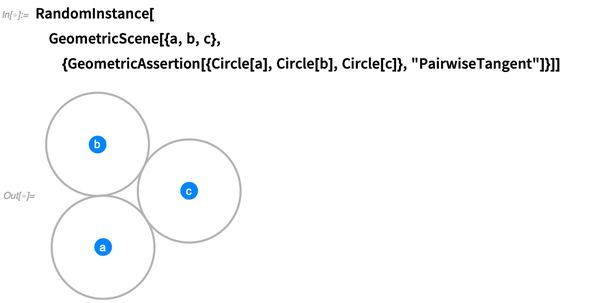
Devenir super-symbolique avec les théories axiomatiques
La version 11.3 a introduit
FindEquationalProof pour générer des représentations symboliques des preuves. Mais quels axiomes devraient être utilisés pour ces preuves? La version 12.0 introduit
AxiomaticTheory , qui donne des axiomes pour diverses
théories axiomatiques courantes.
Voici mon
système d'axiome préféré :
Qu'est-ce que cela signifie? Dans un sens, c'est une expression symbolique plus symbolique que ce à quoi nous sommes habitués. Dans quelque chose comme 1 +
x, nous ne disons pas quelle est la valeur de
x , mais nous imaginons qu'il peut avoir une valeur. Dans l'expression ci-dessus, a, b et c sont de purs «symboles formels» qui remplissent un rôle essentiellement structurel et ne peuvent jamais être considérés comme ayant des valeurs concrètes.
Qu'en est-il du · (point central)? En 1 +
x, nous savons ce que + signifie. Mais le · est destiné à être un opérateur purement abstrait. Le point de l'axiome est en effet de
définir une contrainte sur ce que · peut représenter. Dans ce cas particulier, il s'avère que l'axiome est un
axiome pour l'algèbre booléenne , ce qui peut représenter
Nand et
Nor . Mais nous pouvons déduire les conséquences de l'axiome de manière complètement formelle, par exemple avec
FindEquationalProof :
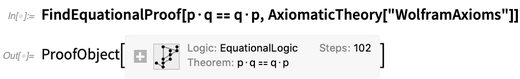
Il y a un peu de subtilité dans tout ça. Dans l'exemple ci-dessus, il est utile d'avoir · comme opérateur, notamment parce qu'il s'affiche bien. Mais il n'y a pas de sens intégré et
AxiomaticTheory vous permet de donner autre chose (ici
f ) en tant qu'opérateur:
Que fait le
«Nand» là-bas? C'est un nom pour l'opérateur (mais il ne doit pas être interprété comme ayant quelque chose à voir avec la valeur de l'opérateur). Dans les
axiomes de la théorie des groupes , par exemple, plusieurs opérateurs apparaissent:
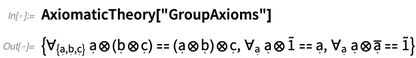
Cela donne ici les représentations par défaut des différents opérateurs:
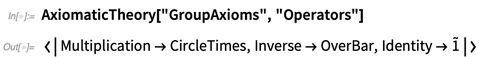AxiomaticTheory connaît des théorèmes notables pour des systèmes axiomatiques particuliers:
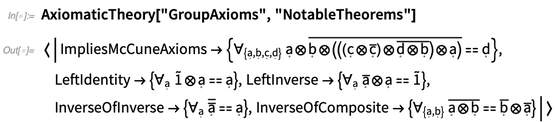
L'idée de base des symboles formels a été introduite dans la version 7, pour faire des choses comme représenter des variables muettes dans des constructions générées comme celles-ci:
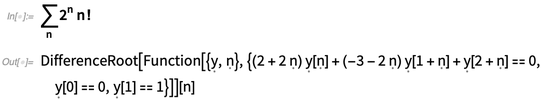
Vous pouvez entrer un symbole formel en utilisant
\ [FormalA] ou Esc, a, Esc, etc. Mais de retour dans la version 7,
\ [FormalA] a été rendu en tant
que . Et cela signifiait que l'expression ci-dessus ressemblait à:
J'ai toujours pensé que cela avait l'air incroyablement compliqué. Et pour la version 12, nous voulions la simplifier. Nous avons essayé de nombreuses possibilités, mais nous avons finalement opté pour des points de repère gris uniques - qui, je pense, sont beaucoup mieux.
Dans
AxiomaticTheory , les variables et les opérateurs sont «purement symboliques». Mais une chose qui est certaine est l'arité de chaque opérateur, que l'on peut demander à
AxiomaticTheory :
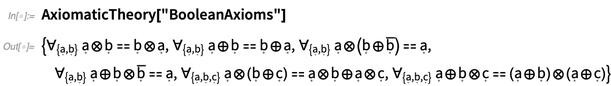
De manière pratique, la représentation des opérateurs et des arités peut être immédiatement introduite dans les
regroupements , pour obtenir des expressions possibles impliquant des variables particulières:
Le problème du n- corps
Les théories axiomatiques représentent un domaine historique classique pour les mathématiques. Un autre domaine historique classique - beaucoup plus du côté appliqué - est le
problème du
n- corps . La version 12.0 introduit
NBodySimulation , qui donne des simulations du problème des n-corps. Voici un problème à trois corps (pensez
Terre-Lune-Soleil ) avec certaines conditions initiales (et loi de force carré inverse):
Vous pouvez poser des questions sur divers aspects de la solution; cela trace les positions en fonction du temps:
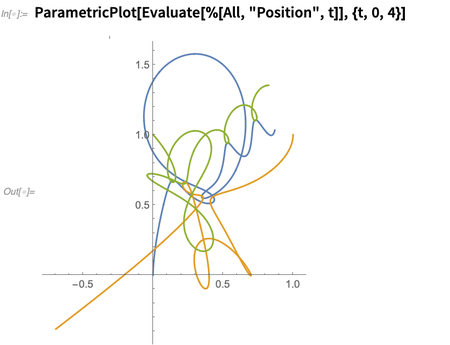
En dessous, cela ne fait que résoudre des équations différentielles, mais - un peu comme
SystemModel -
NBodySimulation fournit un moyen pratique de configurer les équations et de gérer leurs solutions. Et, oui, les lois standard sur la force sont intégrées, mais vous pouvez définir les vôtres.
Extensions linguistiques et commodités
Nous polissons le cœur de Wolfram Language depuis plus de 30 ans maintenant, et dans chaque version successive, nous finissons par introduire de nouvelles extensions et commodités.
Nous avons la fonction
Information depuis la version 1.0, mais dans la version 12.0, nous l'avons considérablement étendue. Il donnait juste des informations sur les symboles (bien que cela ait également été modernisé):
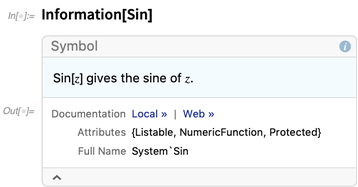
Mais maintenant, il donne également des informations sur de nombreux types d'objets. Voici des informations sur un classificateur:
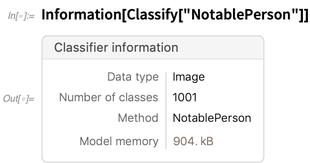
Voici des informations sur un objet cloud:
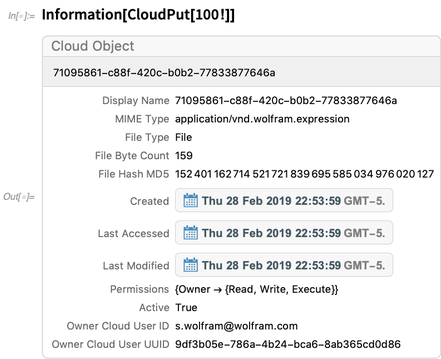
Passez la souris sur les étiquettes dans la «boîte d'informations» et vous pouvez trouver les noms des propriétés correspondantes:
Pour les entités, les
informations donnent un résumé des valeurs de propriété connues:
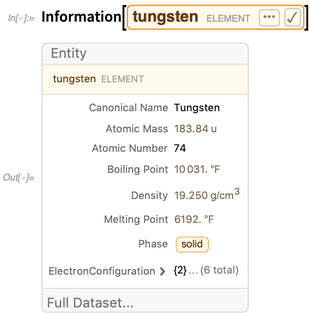
Au cours des dernières versions, nous avons introduit de nombreux nouveaux formulaires d'affichage de résumé. Dans la version 11.3, nous avons introduit
Iconize , qui est essentiellement un moyen de créer un formulaire d'affichage récapitulatif pour n'importe quoi. Iconize s'est avéré encore plus utile que nous l'avions prévu à l'origine. Il est idéal pour masquer une complexité inutile à la fois dans les cahiers et dans des morceaux de code Wolfram Language. Dans la version 12.0, nous avons repensé la façon dont Iconize s'affiche, en particulier pour qu'il soit «bien lu» à l'intérieur des expressions et du code.
Vous pouvez explicitement iconiser quelque chose:
Appuyez sur le + et vous verrez quelques détails:
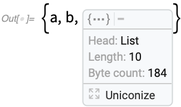
Appuyez sur
et vous obtiendrez à nouveau l'expression originale:
Si vous avez beaucoup de données que vous souhaitez référencer dans un calcul, vous pouvez toujours les stocker dans un fichier, ou dans le
cloud (ou même dans un
référentiel de données ). Cependant, il est généralement plus pratique de simplement le mettre dans votre ordinateur portable, afin que vous ayez tout au même endroit. Une façon d'éviter que les données «prennent le contrôle de votre ordinateur portable» consiste à
mettre des cellules fermées . Mais Iconize offre un moyen beaucoup plus flexible et élégant de le faire.
Lorsque vous écrivez du code, il est souvent pratique de «iconiser en place». Le menu contextuel vous permet désormais de le faire:
En parlant d'affichage, voici quelque chose de petit mais pratique que nous avons ajouté dans 12.0:
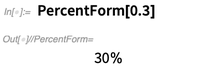
Et voici quelques autres «commodités numériques» que nous avons ajoutées:
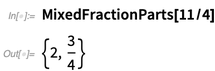
La programmation fonctionnelle a toujours été un élément central du Wolfram Language. Mais nous cherchons continuellement à l'étendre et à introduire de nouvelles primitives généralement utiles. Un exemple dans la version 12.0 est
SubsetMap :
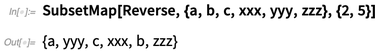
Les fonctions sont normalement des choses qui peuvent prendre plusieurs entrées, mais donnent toujours une seule sortie. Dans des domaines comme
l'informatique quantique , cependant, on souhaite plutôt avoir
n entrées et
n sorties.
SubsetMap implémente efficacement
n-> n fonctions, ramasse les entrées de
n positions spécifiées dans une liste, leur applique des opérations, puis remet les résultats aux mêmes
n positions.
J'ai commencé à formuler ce qui est maintenant
SubsetMap il y a environ un an. Et j'ai rapidement réalisé qu'en fait, j'aurais pu utiliser cette fonction dans toutes sortes d'endroits au fil des ans. Mais comment appeler ce «morceau de travail informatique» particulier? Mon nom de travail initial était
ArrayReplaceFunction (que j'ai raccourci en
ARF dans mes notes). Dans une
séquence de réunions (retransmises en direct), nous avons fait des allers-retours. Il y avait des idées comme
ApplyAt (mais ce n'est pas vraiment
Apply ) et
MutateAt (mais il ne fait pas de mutation au sens de la valeur), ainsi que
RewriteAt ,
ReplaceAt ,
MultipartApply et
ConstructInPlace . Il y avait des idées sur les formulaires «décorateurs de fonctions» au curry, comme
PartAppliedFunction ,
PartwiseFunction ,
AppliedOnto ,
AppliedAcross et
MultipartCurry .
Mais d'une manière ou d'une autre, lorsque nous avons expliqué la fonction, nous avons continué à revenir sur la façon dont elle fonctionnait sur un sous-ensemble d'une liste, et comment elle ressemblait vraiment à
Map , sauf qu'elle fonctionnait sur plusieurs éléments à la fois. Nous avons donc finalement
choisi le nom
SubsetMap . Et - dans un autre renforcement de l'importance de la conception du langage - il est remarquable de voir comment, une fois que l'on a un nom pour quelque chose comme ça, on se trouve immédiatement en mesure de le raisonner et de voir où il peut être utilisé.
Pendant de nombreuses années, nous avons travaillé dur pour faire de Wolfram Language le système de plus haut niveau et le plus automatisé pour effectuer un
apprentissage automatique de pointe . Très tôt, nous avons introduit les «superfonctions» Classify and
Predict qui effectuent des tâches de
classification et de prédiction de manière complètement automatisée, choisissant automatiquement la meilleure approche pour l'entrée donnée donnée. En cours de route, nous avons introduit d'autres superfonctions - comme
SequencePredict ,
ActiveClassification et
FeatureExtract .
Dans la version 12.0, nous avons plusieurs nouvelles fonctions importantes d'apprentissage automatique. Il y a
FindAnomalies , qui trouve des «éléments anormaux» dans les données:
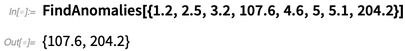
Parallèlement à cela, il y a
DeleteAnomalies , qui supprime les éléments qu'il considère comme anormaux:
Il existe également
SynthesizeMissingValues , qui essaie de générer des valeurs plausibles pour les éléments de données manquants:
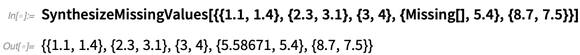
Comment fonctionnent ces fonctions? Ils sont tous basés sur une nouvelle fonction appelée
LearnDistribution , qui essaie d'apprendre la distribution sous-jacente des données, à partir d'un certain ensemble d'exemples. Si les exemples n'étaient que des chiffres, ce serait essentiellement un problème de statistiques standard, pour lequel nous pourrions utiliser quelque chose comme
EstimatedDistribution . Mais le point à propos de
LearnDistribution est qu'il fonctionne avec des données de toute nature, pas seulement des nombres. Ici, il apprend une distribution sous-jacente pour une collection de couleurs:
Une fois que nous avons cette «distribution apprise», nous pouvons faire toutes sortes de choses avec. Par exemple, cela en génère 20 échantillons aléatoires:
Mais pensez maintenant à
FindAnomalies . Ce qu'il doit faire, c'est de savoir quels points de données sont anormaux par rapport à ce qui est attendu. Ou, en d'autres termes, étant donné la distribution sous-jacente des données, il trouve quels points de données sont des valeurs aberrantes, dans le sens où ils ne devraient se produire qu'avec une très faible probabilité selon la distribution.
Et tout comme pour une distribution numérique ordinaire, nous pouvons calculer le
PDF pour une donnée particulière. Le violet est très probable compte tenu de la distribution des couleurs que nous avons apprise de nos exemples:
Mais le rouge est vraiment très improbable:
Pour les distributions numériques ordinaires, il existe des concepts comme
CDF qui nous indiquent les probabilités cumulatives, par exemple que nous obtiendrons des résultats qui sont «plus éloignés» qu'une valeur particulière. Pour les espaces de choses arbitraires, il n'y a pas vraiment de notion de «plus loin». Mais nous avons trouvé une fonction que nous appelons
RarerProbability , qui nous dit quelle est la probabilité totale de générer un exemple avec un PDF plus petit que quelque chose que nous donnons:
Nous avons maintenant un moyen de décrire les anomalies: ce ne sont que des points de données qui ont une très petite probabilité plus rare. Et en fait,
FindAnomalies a une option
AcceptanceThreshold (avec la valeur par défaut 0,001) qui spécifie ce qui doit compter comme «très petit».
OK, mais voyons ce travail sur quelque chose de plus compliqué que les couleurs. Entraînons un détecteur d'anomalie en regardant 1000 exemples de chiffres manuscrits:
Maintenant,
FindAnomalies peut nous dire quels exemples sont anormaux:
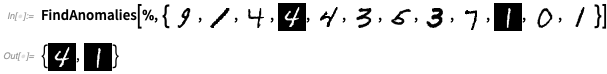
Nous avons introduit notre cadre symbolique pour la construction, l'exploration et l'utilisation de réseaux de neurones en 2016, dans le cadre de la version 11. Et dans chaque version depuis, nous avons ajouté toutes sortes de fonctionnalités de pointe. En juin 2018, nous avons introduit notre
référentiel de
réseaux neuronaux pour faciliter l'accès aux derniers modèles de réseaux neuronaux de Wolfram Language - et il existe déjà près de 100 modèles sélectionnés de nombreux types différents dans le référentiel, avec de nouveaux ajoutés tout le temps.
Donc, si vous avez besoin du dernier
réseau neuronal «transformateur» BERT (qui a été ajouté aujourd'hui!), Vous pouvez l'obtenir auprès de
NetModel :
Vous pouvez l'ouvrir et voir le réseau impliqué (et, oui, nous avons mis à jour l'affichage des graphiques nets pour la version 12.0):
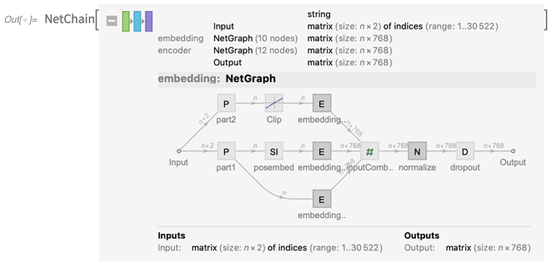
Et vous pouvez immédiatement utiliser le réseau, ici pour produire une sorte de tableau de «caractéristiques significatives»:
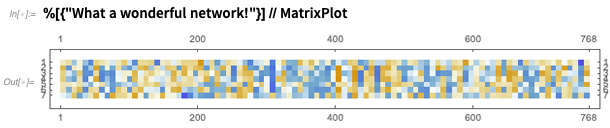
Dans la version 12.0, nous avons introduit plusieurs nouveaux types de couches - notamment
AttentionLayer , qui permet de configurer les dernières architectures de «transformateur» - et nous avons amélioré nos capacités de «programmation fonctionnelle du réseau neuronal», avec des choses comme
NetMapThreadOperator et des séquences multiples
NetFoldOperator . En plus de ces améliorations «à l'intérieur du réseau», la version 12.0 ajoute toutes sortes de nouveaux cas
NetEncoder et
NetDecoder , tels que la
tokenisation BPE pour le texte dans des centaines de langues, et la possibilité d'inclure des fonctions personnalisées pour entrer et sortir des données réseaux neuronaux.
Mais certaines des améliorations les plus importantes de la version 12.0 sont plus infrastructurelles.
NetTrain prend désormais en charge la formation
multi-GPU , ainsi que la gestion de l'arithmétique à précision mixte et des critères d'arrêt précoce flexibles. Nous continuons à utiliser le cadre de réseau neuronal de bas niveau
MXNet (dont nous avons été les
principaux contributeurs ) afin de tirer parti des dernières optimisations matérielles. Il y a de
nouvelles options pour voir ce qui se passe pendant la formation, et il y a aussi
NetMeasurements qui vous permet de faire 33 types de mesures différents sur les performances d'un réseau:
Les réseaux neuronaux ne sont pas le seul - ni même toujours le meilleur - moyen de faire de l'apprentissage automatique. Mais une nouveauté de la version 12.0 est que nous sommes désormais en mesure d'utiliser automatiquement les
réseaux d'auto-normalisation dans
Classify et
Predict , afin qu'ils puissent facilement
profiter des réseaux de neurones quand cela a du sens.
Nous avons introduit
ImageIdentify , pour identifier ce qu'est une image, dans la version 10.1. Dans la version 12.0, nous avons réussi à généraliser cela, à comprendre non seulement ce qu'est une image, mais aussi ce qu'elle contient. Ainsi, par exemple,
ImageCases nous montrera des cas de types d'objets connus dans une image:
Pour plus de détails,
ImageContents fournit un ensemble de données sur le contenu d'une image:
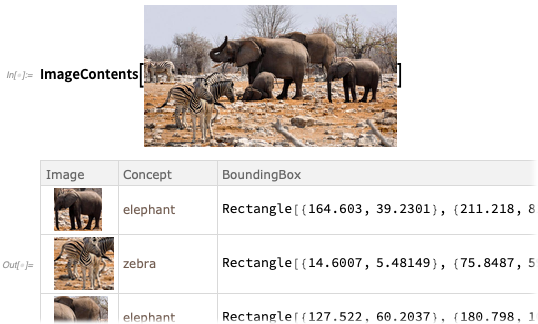
Vous pouvez dire à
ImageCases de rechercher un type particulier de chose:
Et vous pouvez également simplement tester pour voir si une image contient un type particulier de chose:
Dans un sens,
ImageCases est comme une version généralisée de
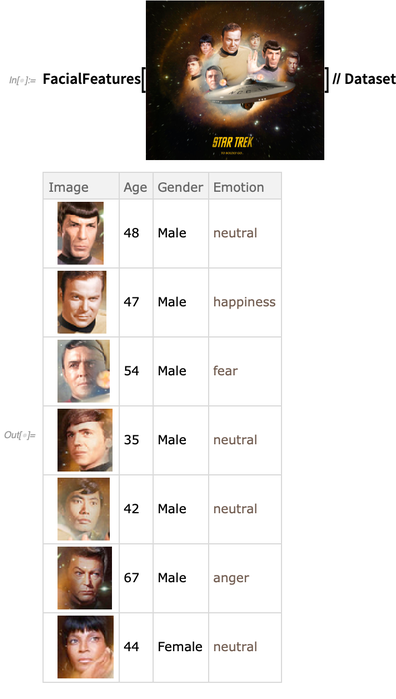
FindFaces , pour trouver des visages humains dans une image. Une nouveauté de la version 12.0 est que les
FindFaces et les
FacialFeatures sont devenues
plus efficaces et plus robustes - avec
FindFaces désormais basé sur des réseaux de neurones plutôt que sur un traitement d'image classique, et le réseau pour
FacialFeatures étant désormais de 10 Mo au lieu de 500 Mo:
Des fonctions comme
ImageCases représentent un traitement d'image «nouveau style», d'un type qui ne semblait pas envisageable il y a seulement quelques années. Mais alors que ces fonctions permettent de faire toutes sortes de nouvelles choses, les techniques plus classiques ont encore beaucoup de valeur. Nous avons depuis longtemps un
traitement d'image classique assez complet en Wolfram Language, mais nous continuons à apporter des améliorations incrémentielles.
Un exemple dans la version 12.0 est le cadre
ImagePyramid , pour effectuer un traitement d'image à plusieurs échelles:
Il existe plusieurs nouvelles fonctions dans la version 12.0 concernant le calcul des couleurs. Une idée clé est
ColorsNear , qui représente un quartier dans l'espace colorimétrique perceptuel, ici autour de la couleur
Rose :
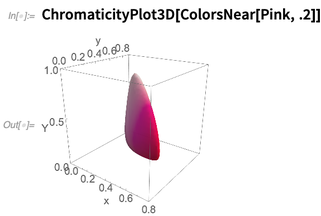
La notion de voisinage de couleur peut être utilisée, par exemple, dans la nouvelle fonction
ImageRecolor :
Alors que je suis assis devant mon ordinateur à écrire ceci, je vais dire quelque chose à mon ordinateur et le
capturer :
Voici un spectrogramme de l'audio que j'ai capturé:
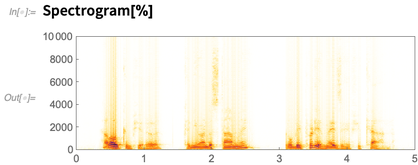
Jusqu'à présent, nous pouvions le faire dans la version 11.3 (bien que
Spectrogram soit 10 fois plus rapide en 12.0). Mais maintenant, voici quelque chose de nouveau:
Nous faisons de la synthèse vocale! Nous utilisons une technologie de réseau neuronal de pointe, mais je suis étonné de voir à quel point cela fonctionne. C'est assez rationalisé, et nous sommes parfaitement capables de gérer même de très longs morceaux d'audio, par exemple stockés dans des fichiers. Et sur un ordinateur typique, la transcription s'exécute à peu près à la vitesse réelle en temps réel, de sorte qu'une heure de parole prendra environ une heure à transcrire.
À l'heure actuelle, nous considérons la
reconnaissance vocale comme expérimentale, et nous continuerons de l'améliorer. Mais il est intéressant de voir une autre tâche informatique majeure devenir une seule fonction dans Wolfram Language.
Dans la version 12.0, il existe également d'autres améliorations.
SpeechSynthesize prend en charge de nouvelles langues et de nouvelles voix (comme répertorié par
VoiceStyleData []).
Il y a maintenant
WebAudioSearch - analogue à
WebImageSearch - qui vous permet de rechercher de l'audio sur le Web:
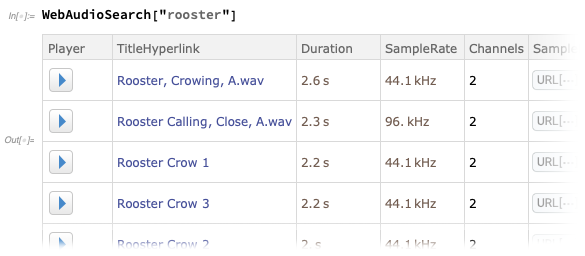
Vous pouvez récupérer des objets
audio réels:
Ensuite, vous pouvez faire des spectrogrammes ou d'autres mesures:
Et puis - nouveau dans la version 12.0 - vous pouvez utiliser
AudioIdentify pour essayer d'identifier la catégorie de son (est-ce un coq qui parle?):
Nous considérons toujours
AudioIdentify expérimental. C'est un début intéressant, mais cela ne fonctionne certainement pas, par exemple, aussi bien que
ImageIdentify .
Une fonction audio plus performante est
PitchRecognize , qui essaie de reconnaître la fréquence dominante dans un signal audio (il utilise à la fois des méthodes «classiques» et neuronales). Il ne peut pas encore traiter les «accords», mais il fonctionne à peu près parfaitement pour les «notes simples».
Quand on traite de l'audio, on veut souvent non seulement identifier ce qu'il y a dans l'audio, mais l'annoter. La version 12.0 introduit le début d'un
cadre audio à grande échelle. À l'heure actuelle,
AudioAnnotate peut indiquer où il y a du silence ou où il y a quelque chose de fort. À l'avenir, nous ajouterons l'identification des locuteurs et les limites des mots, et bien d'autres. Et pour les accompagner, nous avons également des fonctions comme
AudioAnnotationLookup , pour sélectionner des parties d'un objet audio qui ont été annotées de manière particulière.
Sous toutes ces fonctionnalités audio de haut niveau, il y a toute une infrastructure de traitement audio de bas niveau. La version 12.0 améliore considérablement
AudioBlockMap (pour appliquer des filtres aux signaux audio), ainsi que des fonctions comme
ShortTimeFourier .
Un spectrogramme peut être vu un peu comme un analogue continu d'une partition musicale, dans lequel les hauteurs sont tracées en fonction du temps. Dans la version 12.0, il y a maintenant
InverseSpectrogram - qui va d'un tableau de données de spectrogramme à l'audio. Depuis la version 2 en 1991, nous avons eu
Play pour générer du son à partir d'une fonction (comme
Sin [100 t]). Maintenant, avec le
spectrogramme inverse, nous avons un moyen de passer d'un «bitmap fréquence-temps» à un son. (Et, oui, il y a des problèmes délicats concernant les meilleures suppositions pour les phases lorsque l'on ne dispose que d'informations sur la magnitude.)
Depuis
Wolfram | Alpha , nous
possédons depuis longtemps des
capacités exceptionnelles de
compréhension du langage naturel (NLU) . Et cela signifie que, étant donné un morceau de langage naturel, nous sommes bons à le comprendre comme Wolfram Language - que nous pouvons ensuite calculer à partir de:
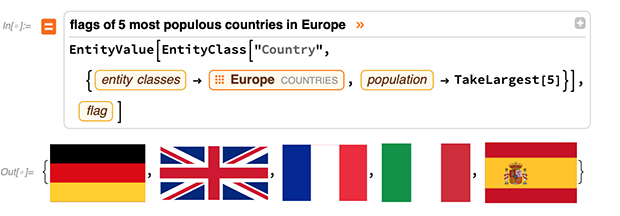
Mais qu'en est-il du traitement du langage naturel (PNL) - où nous prenons potentiellement de longs passages de langage naturel, sans essayer de les comprendre complètement, mais plutôt en trouver ou traiter des caractéristiques particulières? Des fonctions comme
TextSentences ,
TextStructure ,
TextCases et
WordCounts nous ont donné des capacités de base dans ce domaine depuis un certain temps. Mais dans la version 12.0 - en utilisant le dernier apprentissage automatique, ainsi que nos capacités NLU et de base de connaissances de longue date - nous sommes maintenant passés à des capacités NLP très solides.
La pièce maîtresse est la version considérablement améliorée de
TextCases . L'objectif de base de
TextCases est de trouver des cas de différents types de contenu dans un morceau de texte. Un exemple de ceci est la tâche classique de PNL de «reconnaissance d'entité» -
TextCases trouvant ici quels noms de pays apparaissent dans
l'article Wikipedia sur les ocelots :
Nous pourrions également demander quelles îles sont mentionnées, mais maintenant nous ne demanderons pas d'interprétation en langue Wolfram:
TextCases n'est pas parfait, mais il s'en
sort plutôt bien:
Il prend également en charge de nombreux types de contenu différents:
Vous pouvez lui demander de trouver des
pronoms, ou des clauses relatives réduites , ou des
quantités , ou des
adresses e -
mail , ou des occurrences de l'un des 150 types d'entités (comme des
entreprises ou des
usines ou des
films ). Vous pouvez également lui demander de sélectionner des morceaux de texte qui sont en particulier
des langages
humains ou
informatiques , ou qui
concernent des sujets particuliers (comme les
voyages ou la
santé ), ou qui ont
un sentiment positif ou négatif . Et vous pouvez utiliser des constructions comme
Containing pour demander des combinaisons de ces choses (comme des phrases nominales qui contiennent le nom d'une rivière):
TextContents vous permet de voir, par exemple, les détails de toutes les entités qui ont été détectées dans un morceau de texte particulier:
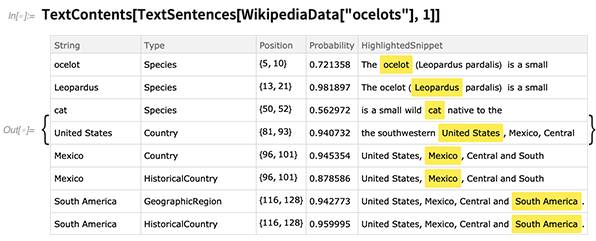
Et, oui, on peut en principe utiliser ces capacités via
FindTextualAnswer pour essayer de répondre aux questions à partir du texte - mais dans un cas comme celui-ci, les résultats peuvent être assez farfelus:
Bien sûr, vous pouvez obtenir une vraie réponse de notre base de connaissances organisée actuelle:
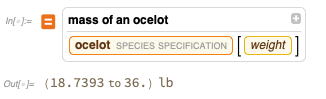
Soit dit en passant, dans la version 12.0, nous avons ajouté une variété de petites «fonctions pratiques en langage naturel», comme les
synonymes et les
antonymes :
L'un des nouveaux domaines «surprenants» de la version 12.0 est la chimie numérique. Nous avons depuis longtemps des données sur
des produits chimiques connus explicites dans notre base de connaissances. Mais dans la version 12.0, nous pouvons calculer avec des molécules qui sont spécifiées simplement comme des objets symboliques purs. Voici comment spécifier ce qui se révèle être une molécule d'eau:
Et voici comment faire un rendu 3D:
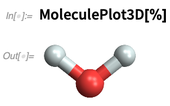
Nous pouvons traiter des «produits chimiques connus»:
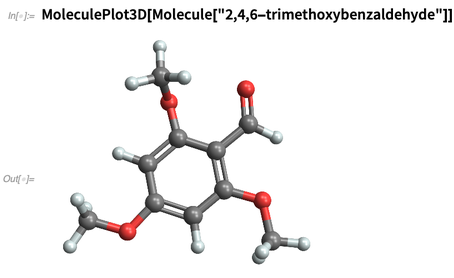
Nous pouvons utiliser des noms
IUPAC arbitraires:
Ou nous «composons» des produits chimiques, par exemple en les spécifiant par leurs chaînes
SMILES :
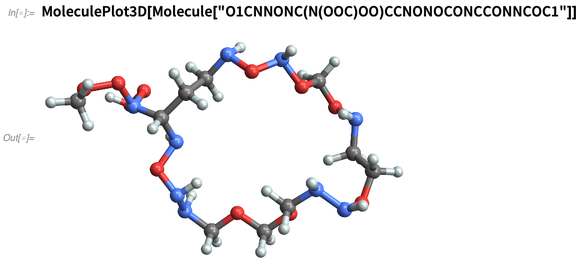
Mais nous ne générons pas seulement des images ici. Nous pouvons également calculer des choses à partir de la structure - comme des symétries:
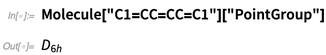
Étant donné une molécule, nous pouvons faire des choses comme mettre en évidence les liaisons carbone-oxygène:
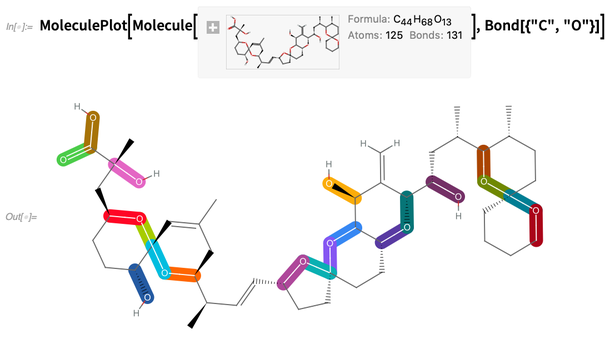
Ou mettez en surbrillance les structures, par exemple spécifiées par les chaînes
SMARTS (ici n'importe quel anneau à 5 membres):
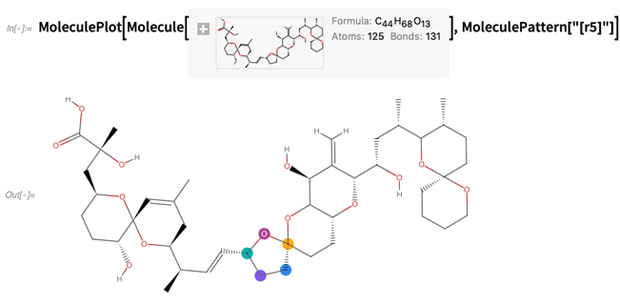
Vous pouvez également effectuer des recherches sur les «modèles de molécules»; les résultats sortent en termes de nombres d'atomes:
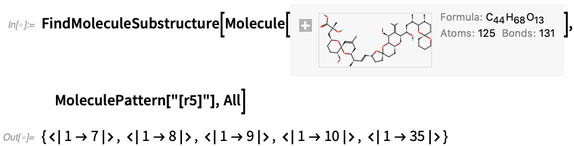
Les capacités de chimie computationnelle que nous avons ajoutées dans la version 12.0 sont assez générales et assez puissantes (avec la réserve que jusqu'à présent, elles ne traitent que des molécules organiques). Au niveau le plus bas, ils voient les molécules comme des graphiques étiquetés avec des bords correspondant aux liaisons. Mais ils connaissent aussi la physique et tiennent correctement compte des valences atomiques et des configurations de liaisons. Inutile de dire qu'il y a beaucoup de détails (sur la stéréochimie, la symétrie, l'aromaticité, les isotopes, etc.). Mais le résultat final est que la structure moléculaire et le calcul moléculaire ont maintenant été ajoutés avec succès à la liste des domaines qui sont intégrés dans le Wolfram Language.
Le Wolfram Language possède déjà de fortes capacités pour l'informatique géographique, mais la version 12.0 ajoute plus de fonctions et améliore certaines de celles qui étaient déjà là.
Par exemple, il y a maintenant
RandomGeoPosition , qui génère un emplacement aléatoire lat-long. On pourrait penser que ce serait trivial, mais bien sûr, il faut se soucier des transformations de coordonnées - et ce qui le rend beaucoup plus non trivial, c'est qu'on peut lui dire de choisir des points uniquement à l'intérieur d'une certaine région, ici le pays de la France:
Un thème des nouvelles capacités géographiques de la version 12.0 traite non seulement les points et régions géographiques, mais aussi les vecteurs géographiques. Voici le vecteur vent actuel, par exemple, à la position de la Tour Eiffel, représentée comme un
GeoVector , avec la vitesse et la direction (il y a aussi
GeoVectorENU , qui donne les composants est, nord et haut, ainsi que
GeoGridVector et
GeoVectorXYZ ):
Des fonctions comme
GeoGraphics vous permettent de visualiser des vecteurs géographiques discrets.
GeoStreamPlot est l'analogue géo de
StreamPlot (ou
ListStreamPlot ) —et montre des lignes de flux formées à partir de géo-vecteurs (ici de
WindDirectionData ):
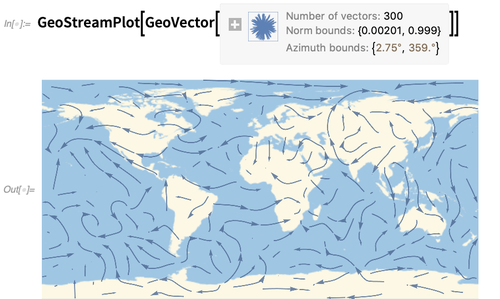
La géodésie est un domaine mathématiquement sophistiqué, et nous sommes fiers de bien le faire dans la langue Wolfram. Dans la version 12.0, nous avons ajouté quelques nouvelles fonctions pour compléter certains détails. Par exemple, nous avons maintenant des fonctions comme
GeoGridUnitDistance et
GeoGridUnitArea qui donnent la distorsion (fondamentalement, les valeurs propres du jacobien) associées à différentes projections géographiques à chaque position sur Terre (ou Lune, Mars, etc.).
Une direction de la visualisation que nous développons régulièrement est ce que l'on pourrait appeler des «méta-graphiques»: l'étiquetage et l'annotation de choses graphiques. Nous avons introduit
Callout dans la version 11.0; dans la version 12.0, il a été étendu à des choses comme les graphiques 3D:
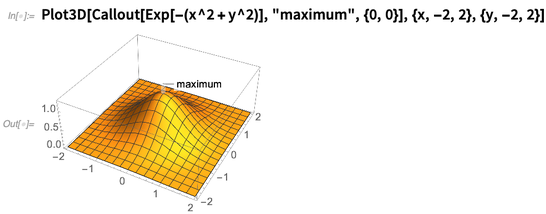
Il est assez bon pour savoir où étiqueter les choses, même lorsqu'elles deviennent un peu complexes:
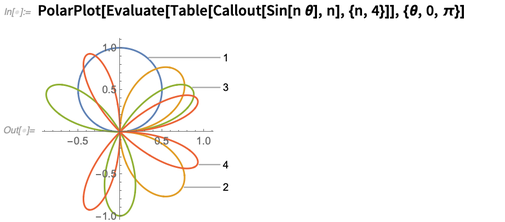
Il y a beaucoup de détails qui comptent pour que les graphismes soient vraiment beaux. Quelque chose qui a été amélioré dans la version 12.0 est de s'assurer que les colonnes de graphiques s'alignent sur leurs cadres, quelle que soit la longueur de leurs étiquettes de graduation. Nous avons également ajouté
LabelVisibility , qui vous permet de spécifier les priorités relatives avec lesquelles différentes étiquettes doivent être rendues visibles.
Une autre nouvelle fonctionnalité de la version 12.0 est la disposition de tracé à plusieurs niveaux, où différents jeux de données sont affichés dans différents panneaux, mais les panneaux partagent des axes chaque fois qu'ils le peuvent:
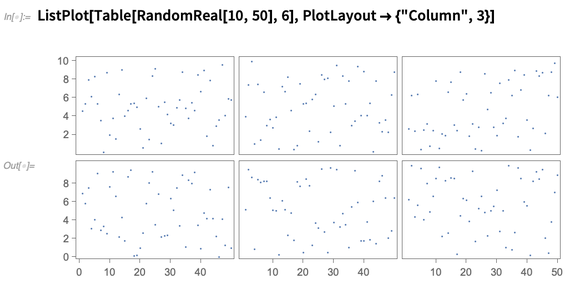
Renforcement de l'intégration de la base de connaissances
Notre base de connaissances organisée - qui alimente par exemple
Wolfram | Alpha - est vaste et en constante expansion. Et avec chaque version de Wolfram Language, nous resserrons progressivement son intégration au cœur de la langue.
Dans la version 12.0, nous essayons d'exposer des centaines de types d'entités directement dans le langage:
Avant la version 12.0, les
pages d'exemples Wolfram | Alpha servaient de proxy pour documenter de nombreux types d'entités. Mais maintenant, il existe une documentation Wolfram Language pour chacun d'eux:
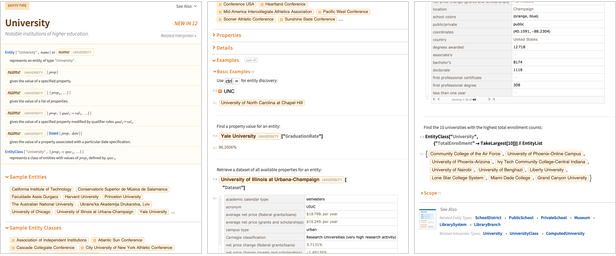
Il existe encore des fonctions telles que
SatelliteData ,
WeatherData et
FinancialData qui gèrent les types d'entité qui nécessitent régulièrement une sélection ou un calcul complexe. Mais dans la version 12.0, chaque type d'entité est accessible de la même manière, avec
une entrée en
langage naturel («contrôle + =») et des entités et propriétés «en boîte jaune»:
Soit dit en passant, on peut également utiliser des entités implicitement, comme ici en demandant les 5 éléments avec les plus hauts points de fusion connus:
Et on peut utiliser
Dated pour obtenir une série chronologique de valeurs:
Nous avons simplifié l'utilisation des données intégrées à la base de
connaissances Wolfram . Vous avez des entités, et il est très facile de poser des questions sur les propriétés, etc.:
Mais que faire si vous avez vos propres données? Pouvez-vous le configurer pour pouvoir l'utiliser aussi facilement que cela? Une
nouvelle fonctionnalité majeure de la version 11 a été l'ajout d'
EntityStore , dans lequel on peut
définir ses propres types d'entités , puis spécifier des entités, des propriétés et des valeurs.
Le
référentiel de données Wolfram contient un
tas d'exemples de magasins d'entités . En voici un:
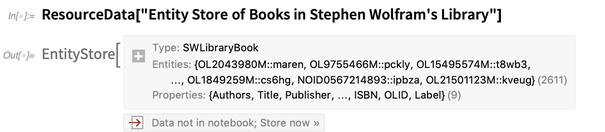
Il décrit un seul type d'entité: un
"SWLibraryBook" . Pour pouvoir utiliser des entités de ce type comme des entités intégrées, nous «enregistrons» le magasin d'entités:
Maintenant, nous pouvons faire des choses comme demander 10 entités aléatoires de type
"SWLibraryBook" :
Chaque entité du magasin d'entités a une variété de propriétés. Voici un ensemble de données des valeurs des propriétés pour une entité particulière:
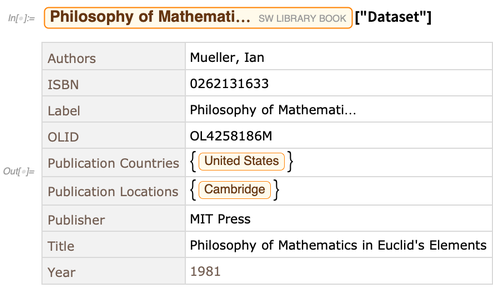
D'accord, mais avec cette configuration, nous lisons fondamentalement tout le contenu d'un magasin d'entités en mémoire. Cela le rend très efficace pour faire toutes les opérations de Wolfram Language que l'on veut. Mais ce n'est pas une bonne solution évolutive pour de grandes quantités de données - par exemple, des données trop volumineuses pour tenir en mémoire.
Mais quelle est une source typique de données volumineuses? Très souvent, il s'agit d'une base de données, et généralement relationnelle accessible à l'aide de
SQL . Nous avons notre
package DatabaseLink pour un accès en lecture-écriture de bas niveau aux bases de données SQL depuis plus d'une décennie. Mais dans la version 12.0, nous ajoutons des fonctionnalités intégrées majeures qui permettent de gérer les bases de données relationnelles externes dans le langage Wolfram tout comme les magasins d'entités, ou les parties intégrées de la base de connaissances Wolfram.
Commençons par un exemple de jouet. Voici une représentation symbolique d'une petite base de données relationnelle qui se trouve être stockée dans un fichier:
Immédiatement, nous obtenons une boîte qui résume le contenu de la base de données et nous indique que cette base de données contient 8 tables. Si nous ouvrons la boîte, nous pouvons commencer à inspecter la structure de ces tables:
Nous pouvons ensuite configurer cette base de données relationnelle comme un magasin d'entités dans Wolfram Language. Il ressemble beaucoup au magasin d'entités de livres de bibliothèque ci-dessus, mais maintenant les données réelles ne sont pas stockées en mémoire; au lieu de cela, il est toujours dans la base de données relationnelle externe, et nous ne faisons que définir un mappage («semblable à ORM») aux entités dans le langage Wolfram:
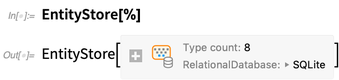
Maintenant, nous pouvons enregistrer ce magasin d'entités, qui configure un tas de types d'entités qui (au moins par défaut) sont nommés d'après les noms des tables de la base de données:
Et maintenant, nous pouvons faire des «calculs d'entités» sur ces derniers, tout comme nous le ferions sur des entités intégrées dans la base de connaissances Wolfram. Chaque entité correspond ici à une ligne du tableau «salariés» de la base de données:
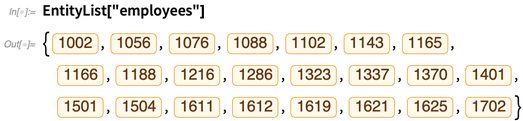
Pour un type d'entité donné, nous pouvons demander quelles propriétés il possède. Ces «propriétés» correspondent aux colonnes du tableau dans la base de données sous-jacente:
Maintenant, nous pouvons demander la valeur d'une propriété particulière d'une entité particulière:
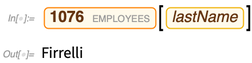
Nous pouvons également sélectionner des entités en donnant des critères; ici, nous demandons des entités de «paiements» avec les 4 plus grandes valeurs de la propriété «montant»:
On peut également demander les valeurs de ces montants les plus importants:
D'accord, mais voici où cela devient plus intéressant: jusqu'à présent, nous avons examiné une petite base de données sauvegardée sur fichiers. Mais nous pouvons faire exactement la même chose avec une base de données géante hébergée sur un serveur externe.
À titre d'exemple, connectons-nous à la
base de données OpenStreetMap PostgreSQL de taille téraoctet qui contient ce qui est essentiellement la carte routière du monde:
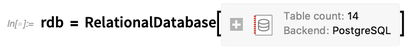
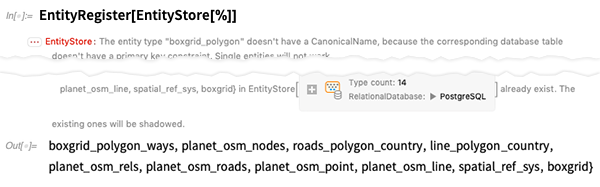
Comme précédemment, enregistrons les tables de cette base de données en tant que types d'entités. Comme la plupart des bases de données naturelles, il y a peu de problèmes dans la structure, qui sont contournés, mais génèrent des avertissements:
Mais maintenant, nous pouvons poser des questions sur la base de données - comme le nombre de points géographiques ou de «nœuds» dans toutes les rues du monde (et, oui, c'est un grand nombre, c'est pourquoi la base de données est grande):
Ici, nous demandons les noms des objets avec les 10 plus grandes zones (projetées) dans la table planet_osm_polygon (101 Go) (et, oui, cela prend moins d'une seconde):
Alors, comment ça marche? Fondamentalement, ce qui se passe, c'est que notre représentation Wolfram Language est compilée dans des requêtes SQL de bas niveau qui sont ensuite envoyées pour être exécutées directement sur le serveur de base de données.
Parfois, vous demanderez des résultats qui ne sont que des valeurs finales (comme, par exemple, les «montants» ci-dessus). Mais dans d'autres cas, vous voudrez quelque chose d'intermédiaire - comme une collection d'entités qui ont été sélectionnées d'une manière particulière. Et bien sûr, cette collection pourrait avoir un milliard d'entrées. Donc, une caractéristique très importante de ce que nous introduisons dans la version 12.0 est que nous pouvons représenter et manipuler ces choses de manière purement symbolique, en les résolvant à quelque chose de spécifique uniquement à la fin.
Pour en revenir à notre base de données de jouets, voici un exemple de la façon dont nous spécifierions une classe d'entités obtenue en agrégeant le
CreditLimit total pour tous les
clients avec une valeur de
pays donnée:
Au début, c'est juste quelque chose de symbolique. Mais si nous demandons des valeurs spécifiques, les requêtes de base de données réelles sont effectuées et nous obtenons des résultats spécifiques:
Il existe une famille de nouvelles fonctions pour configurer différents types de requêtes. Et les fonctions fonctionnent réellement non seulement pour les bases de données relationnelles, mais aussi pour les magasins d'entités et pour la base de connaissances Wolfram intégrée. Ainsi, par exemple, nous pouvons demander la masse atomique moyenne pour une période donnée dans le
tableau périodique des éléments :
Une nouvelle construction importante est
EntityFunction .
EntityFunction est comme
Function , sauf que ses variables représentent des entités (ou des classes d'entités) et il décrit des opérations qui peuvent être effectuées directement sur des bases de données externes. Voici un exemple avec des données intégrées, dans lequel nous définissons une classe d'entités «filtrée» dans laquelle le critère de filtrage est une fonction qui teste les valeurs de population. Le
FilteredEntityClass lui-même est simplement représenté symboliquement, mais
EntityList exécute en fait la requête et résout une liste explicite d'entités (ici, non triées):
Outre
EntityFunction ,
AggregatedEntityClass et
SortedEntityClass , la version 12.0 inclut
SampledEntityClass (pour obtenir quelques entités d'une classe),
ExtendedEntityClass (pour ajouter des propriétés calculées) et
CombinedEntityClass (pour combiner les propriétés de différentes classes). Avec ces primitives, on peut construire toutes les opérations standard de "l'
algèbre relationnelle ".
Dans la programmation de base de données standard, on se retrouve généralement avec une jungle entière de «jointures» et de «clés étrangères» et ainsi de suite. Notre représentation Wolfram Language vous permet d'opérer à un niveau supérieur - où les jointures deviennent fondamentalement une composition de fonctions et les clés étrangères ne sont que différents types d'entités. (Si vous souhaitez effectuer des jointures explicites, vous pouvez, par exemple, utiliser
CombinedEntityClass .)
Ce qui se passe sous le capot, c'est que toutes ces constructions Wolfram Language sont compilées en SQL, ou, plus précisément, le dialecte spécifique de
SQL qui convient à la base de données particulière que vous utilisez (nous prenons actuellement en charge
SQLite ,
MySQL ,
PostgreSQL et
MS -SQL , avec prise en charge d'
OracleSQL à venir). Lorsque nous faisons la compilation, nous vérifions automatiquement les types, pour nous assurer que vous obtenez une requête significative. Même des spécifications Wolfram Language assez simples peuvent finir par se transformer en plusieurs lignes de SQL. Par exemple,
produirait le SQL intermédiaire suivant (ici pour interroger la base de données SQLite):
Le système d'intégration de base de données que nous avons dans la version 12.0 est assez sophistiqué - et nous y travaillons depuis pas mal d'années. C'est un pas en avant important pour permettre au Wolfram Language de gérer directement un nouveau niveau de «bigness» dans les mégadonnées - et de permettre au Wolfram Language d'effectuer directement la science des données sur des ensembles de données de taille téraoctet et au-delà. Comme trouver quelles entités semblables à des rues dans le monde ont «Wolfram» dans leur nom:
Quelle est la meilleure façon de représenter la connaissance du monde? C'est une question qui a été débattue par les philosophes (et d'autres) depuis l'antiquité. Parfois, les gens disaient que la logique était la clé. Parfois des mathématiques. Parfois des bases de données relationnelles. Mais maintenant, nous connaissons au moins une base solide (ou du moins, je suis presque sûr que nous le savons): tout peut être représenté par le calcul. C'est une idée puissante - et dans un sens, c'est ce qui rend possible tout ce que nous faisons avec Wolfram Language.
Mais existe-t-il des sous-ensembles de calcul général qui sont utiles pour représenter au moins certains types de connaissances? L'une que nous utilisons largement dans la base de
connaissances Wolfram est la notion d'entités ("New York City"), de propriétés ("population") et de leurs valeurs ("8,6 millions de personnes"). Bien sûr, ces triplets ne représentent pas toute la connaissance du monde («quelle sera la position de Mars demain?»). Mais ils constituent un bon départ en ce qui concerne certains types de connaissances «statiques» sur des choses distinctes.
Comment formaliser ce type de représentation des connaissances? Une réponse est par le biais de bases de données graphiques. Et dans la version 12.0 - en alignement avec de nombreux projets de
«Web sémantique» - nous prenons en charge les
bases de données graphiques à l' aide de
RDF et les requêtes contre elles à l'aide de
SPARQL . Dans RDF, l'objet central est un
IRI («Internationalized Resource Identifier»), qui peut représenter une entité ou une propriété. Un «
triplestore » consiste alors en une collection de triplets («sujet», «prédicat», «objet»), chaque élément de chaque triplet étant un IRI (ou un littéral, tel qu'un nombre). L'objet entier peut alors être considéré comme une base de données de graphes ou un magasin de graphes, ou, mathématiquement, un hypergraphe. (C'est un
hypergraphe parce que les «bords» prédicats peuvent également être des sommets ailleurs.)
Vous pouvez créer votre propre
RDFStore un peu comme vous
créez un
EntityStore - et en fait, vous pouvez interroger n'importe quel Wolfram Language
EntityStore à l' aide de SPARQL, tout comme vous interrogez un
RDFStore . Et comme la partie entité-propriété de la base de connaissances Wolfram peut être traitée comme un magasin d'entités, vous pouvez également l'interroger. Voici donc enfin un exemple. La liste pays-ville
Entité ["
Pays "],
Entité ["
Ville "]} représente en effet un magasin RDF. Ensuite,
SPARQLSelect est un opérateur agissant sur ce magasin. Ce qu'il fait, c'est d'essayer de trouver un triple qui correspond à ce que vous demandez, avec une valeur particulière pour la «variable SPARQL» x:
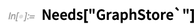
Bien sûr, il existe également un moyen beaucoup plus simple de le faire dans le Wolfram Language:
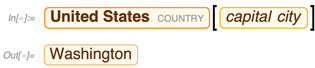
Mais avec SPARQL, vous pouvez faire des choses beaucoup plus exotiques - comme demander quelles propriétés relient les États-Unis au Mexique:
Ou s'il existe un chemin basé sur la relation du pays limitrophe du Portugal à l'Allemagne:
En principe, vous pouvez simplement écrire une requête SPARQL sous forme de chaîne (un peu comme vous pouvez écrire une chaîne SQL). Mais ce que nous avons fait dans la version 12.0, c'est introduire une représentation symbolique de SPARQL qui permet le calcul sur la représentation elle-même, ce qui facilite, par exemple, la génération automatique de requêtes SPARQL complexes. (Et il est particulièrement important de le faire car, en soi, les requêtes SPARQL pratiques ont l'habitude de devenir extrêmement longues et lourdes.)
D'accord, mais y a-t-il des magasins RDF à l'état sauvage? C'est un espoir de longue date qu'une grande partie du Web sera en quelque sorte suffisamment étiquetée pour «devenir sémantique» et en fait être un magasin RDF géant. Ce serait formidable si cela se produisait, mais jusqu'à présent, ce n'est certainement pas le cas. Pourtant, il existe quelques magasins RDF publics, ainsi que certains magasins RDF au sein des organisations, et avec nos nouvelles capacités dans la version 12.0, nous sommes dans une position unique pour faire des choses intéressantes avec eux.
Une forme de problème incroyablement courante dans les applications industrielles des mathématiques est: «Quelle configuration minimise le coût (ou maximise le gain) si certaines contraintes doivent être satisfaites?» Il y a plus d'un demi-siècle, le soi-disant
algorithme simplex a été inventé pour résoudre des versions linéaires de ce type de problème, dans lesquelles la fonction objectif (coût, gain) et les contraintes sont des fonctions linéaires des variables du problème. Dans les années 80, des méthodes beaucoup plus efficaces («point intérieur») avaient été inventées - et nous en avons depuis longtemps pour faire de la «
programmation linéaire » en Wolfram Language.
Mais qu'en est-il des problèmes non linéaires? Eh bien, dans le cas général, on peut utiliser des fonctions comme NMinimize. Et ils font un travail de pointe. Mais c'est un problème difficile. Cependant, il y a quelques années, il est devenu clair que même parmi les problèmes d'optimisation non linéaire, il existe une classe de problèmes d'optimisation dits convexes qui peuvent en fait être résolus presque aussi efficacement que les problèmes linéaires. («Convexe» signifie que l'objectif et les contraintes n'impliquent que des fonctions convexes - de sorte que rien ne peut «bouger» à l'approche d'un extremum, et il ne peut y avoir de minima locaux qui ne soient pas des minima globaux.)
Dans la version 12.0, nous avons maintenant des implémentations solides pour toutes les différentes classes standard d'optimisation convexe. Voici un cas simple, impliquant la minimisation d'une forme quadratique avec quelques contraintes linéaires:
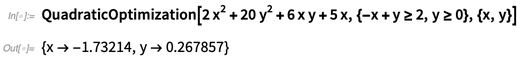NMinimize pouvait déjà résoudre ce problème particulier dans la version 11.3:
Mais si l'on avait plus de variables, l'ancien
NMinimize s'enliserait rapidement. Dans la version 12.0, cependant,
Quadratic Optimization continuera de fonctionner correctement, jusqu'à plus de 100 000 variables avec plus de 100 000 contraintes (tant qu'elles sont assez clairsemées).
Dans la version 12.0, nous avons des fonctions «d'optimisation convexe brute» comme
SemidefiniteOptimization (qui gère les inégalités matricielles linéaires) et
ConicOptimization (qui gère les inégalités vectorielles linéaires). Mais des fonctions comme
NMinimize et
FindMinimum reconnaîtront également automatiquement quand un problème peut être résolu efficacement en étant transformé en une forme d'optimisation convexe.
Comment mettre en place des problèmes d'optimisation convexe? Les plus grands impliquent des contraintes sur des vecteurs entiers ou des matrices de variables. Et dans la version 12.0, nous avons maintenant des fonctions comme
VectorGreaterEqual (entrée comme ≥) qui peuvent immédiatement les représenter.
Les équations différentielles partielles sont difficiles, et nous travaillons depuis 30 ans sur des moyens de plus en plus sophistiqués et généraux de les gérer. Nous avons introduit
NDSolve (pour les ODE) pour la première fois dans la
version 2, en 1991 . Nous avions nos premiers PDE numériques (1 + 1 dimension) au milieu des années 1990. En 2003, nous avons introduit notre cadre modulaire puissant pour gérer les équations différentielles numériques. Mais en termes de PDE, nous ne nous occupions encore que de régions rectangulaires simples. Pour aller au-delà de cela, il a fallu construire l'ensemble de notre
système de géométrie informatique , que nous avons introduit dans la version 10. Et avec cela, nous avons sorti
nos premiers solveurs PDE à éléments finis . Dans la version 11, nous avons ensuite généralisé aux
problèmes propres .
Maintenant, dans la version 12, nous introduisons une autre généralisation majeure: l'analyse par éléments finis non linéaire. L'analyse par éléments finis implique la décomposition des régions en petits triangles discrets, tétraèdres, etc. - sur lesquels la PDE d'origine peut être approximée par un grand nombre d'équations couplées. Lorsque l'EDP d'origine est linéaire, ces équations seront également linéaires - et c'est le cas typique que les gens considèrent lorsqu'ils parlent d '«analyse par éléments finis».
Mais il existe de nombreux PDE d'importance pratique qui ne sont pas linéaires - et pour y remédier, il faut une analyse par éléments finis non linéaire, ce que nous avons maintenant dans la version 12.0.
À titre d'exemple, voici ce qu'il faut pour résoudre le PDE méchamment non linéaire qui décrit la hauteur d'une surface minimale 2D (par exemple, un film de savon idéalisé), ici sur un anneau, avec des conditions aux limites (Dirichlet) qui le font se tortiller sinusoïdalement à la bords (comme si le film de savon était suspendu à des fils):
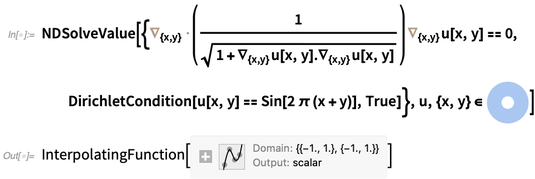
Sur mon ordinateur, il suffit d'un quart de seconde pour résoudre cette équation et obtenir une fonction d'interpolation. Voici un tracé de la fonction d'interpolation représentant la solution:
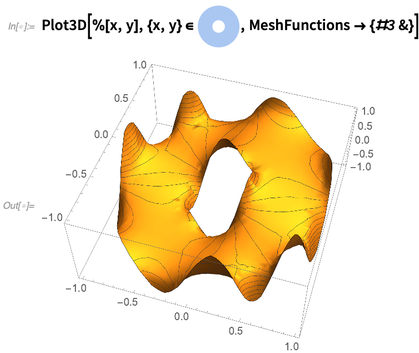
Nous avons mis beaucoup d'ingénierie pour optimiser l'exécution des programmes Wolfram Language au fil des ans. Déjà en 1989, nous avons commencé à compiler automatiquement des calculs numériques simples de précision machine en instructions pour une machine virtuelle efficace (et, en l'occurrence, j'ai écrit le code original pour cela). Au fil des ans, nous avons étendu les capacités de ce compilateur, mais il a toujours été limité à des programmes assez simples.
Dans la version 12.0, nous faisons un grand pas en avant et nous publions la première version d'un nouveau compilateur beaucoup plus puissant sur lequel nous travaillons depuis plusieurs années. Ce compilateur est à la fois capable de gérer une gamme beaucoup plus large de programmes (y compris des constructions fonctionnelles complexes et des flux de contrôle élaborés), et il compile non pas sur une machine virtuelle mais directement sur un code machine natif optimisé.
Dans la version 12.0, nous considérons toujours le nouveau compilateur comme expérimental. Mais cela progresse rapidement et cela va avoir un effet dramatique sur l'efficacité de beaucoup de choses dans la langue Wolfram. Dans la version 12.0, nous exposons simplement une «forme de kit» du nouveau compilateur, avec des fonctions de compilation spécifiques. Mais nous allons progressivement faire fonctionner le compilateur de plus en plus automatiquement - déterminer avec l'apprentissage automatique et d'autres méthodes quand cela vaut la peine de prendre le temps de faire quel niveau de compilation.
Au niveau technique, le nouveau compilateur de la version 12.0 est basé sur LLVM et fonctionne en générant du code LLVM - en liant dans la même bibliothèque d'exécution de bas niveau que le noyau Wolfram Language lui-même utilise, et en rappelant le noyau Wolfram Language complet pour la fonctionnalité qui n'est pas dans la bibliothèque d'exécution.
Voici la manière de base de compiler une fonction pure dans la version actuelle du nouveau compilateur:
La fonction de code compilée résultante fonctionne exactement comme la fonction d'origine, mais plus rapidement:
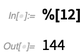
Une grande partie de ce qui permet à
FunctionCompile de produire une fonction plus rapide est que vous lui dites de faire des hypothèses sur le type d'argument qu'il obtiendra. Nous prenons en charge de nombreux types de base (comme "
Integer32 " et "
Real64 "). Mais lorsque vous utilisez
FunctionCompile , vous vous engagez sur des types d'arguments particuliers, donc beaucoup plus de code rationalisé peut être produit.
Une grande partie de la sophistication du nouveau compilateur est associée à la déduction des types de données qui seront générés lors de l'exécution d'un programme. (Il y a beaucoup d'algorithmes théoriques et autres graphiques impliqués, et il va sans dire que toute la métaprogrammation pour le compilateur se fait avec le Wolfram Language.)
Voici un exemple qui implique un peu d'inférence de type (le type de
fib est déduit pour être
"Integer64" -> "Integer64" : une fonction entière retournant un entier):
Sur mon ordinateur,
cf [25] fonctionne environ 300 fois plus vite que la fonction non compilée. (Bien sûr, la version compilée échoue lorsque sa sortie n'est plus de type "
Integer64 ", mais la version standard de Wolfram Language continue de bien fonctionner.)
Le compilateur peut déjà gérer des centaines de primitives de programmation Wolfram Language, en suivant de manière appropriée les types produits et en générant du code qui implémente directement ces primitives. Parfois, cependant, on voudra utiliser des fonctions sophistiquées dans le Wolfram Language pour lesquelles cela n'a pas de sens de générer son propre code compilé - et où ce que l'on veut vraiment faire est simplement d'appeler dans le noyau Wolfram Language pour ces fonctions . Dans la version 12.0,
KernelFunction permet de faire ceci:
D'accord, mais disons qu'on a une fonction de code compilé. Que peut-on en faire? Eh bien, tout d'abord, on peut simplement l'exécuter dans le Wolfram Language. On peut aussi le stocker et l'exécuter plus tard. Toute compilation particulière est effectuée pour une architecture de processeur spécifique (par exemple 64 bits x86). Mais
CompiledCodeFunction conserve automatiquement suffisamment d'informations pour effectuer une compilation supplémentaire pour une architecture différente si nécessaire.
Mais étant donné un
CompiledCodeFunction , l'une des nouvelles possibilités intéressantes est que l'on peut générer directement du code qui peut être exécuté même en dehors de l'environnement Wolfram Language. (Notre ancien compilateur avait le package
CCodeGenerate qui fournissait des capacités légèrement similaires dans des cas simples - bien que même alors, il repose sur une chaîne d'outils élaborée de compilateurs C, etc.)
Voici comment on peut exporter du code LLVM brut (notez que des choses comme l'optimisation de la récursivité de queue se font automatiquement - et notez également la fonction symbolique et les options du compilateur à la fin):
Si l'on utilise
FunctionCompileExportLibrary , alors on obtient un fichier de bibliothèque - .dylib sur Mac, .dll sur Windows et .so sur Linux. On peut utiliser cela dans le Wolfram Language en faisant
LibraryFunctionLoad . Mais on peut aussi l'utiliser dans un programme externe.
L'une des principales choses qui détermine la généralité du nouveau compilateur est la richesse de son système de types. À l'heure actuelle, le compilateur prend en charge
14 types atomiques (tels que "
Boolean ", "
Integer8 ", "
Complex64 ", etc.). Il prend également en charge les constructeurs de types tels que "
PackedArray " - de sorte que, par exemple,
TypeSpecifier ["
PackedArray "] [
"Real64", 2 ] correspond à un tableau compact de rang 2 de réels 64 bits.
Dans l'implémentation interne de Wolfram Language (qui, soit dit en passant, est lui-même principalement en Wolfram Language), nous avons depuis longtemps optimisé le stockage des tableaux. Dans la version 12.0, nous l'
exposons en tant que
NumericArray . Contrairement aux constructions Wolfram Language ordinaires, vous devez expliquer en détail à
NumericArray comment il doit stocker les données. Mais alors cela fonctionne d'une manière agréable et optimisée:
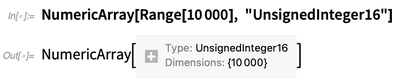
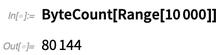
Dans la version 11.2, nous avons introduit
ExternalEvaluate , qui vous permet de faire des calculs dans des langages comme
Python et
JavaScript à partir du Wolfram Language (en
Python , «^» signifie
BitXor ):
Dans la version 11.3, nous avons introduit des cellules de langue externes, pour faciliter la saisie de programmes en langues externes ou d'autres entrées directement dans un ordinateur portable:
Dans la version 12.0, nous resserrons l'intégration. Par exemple, à l'intérieur d'une chaîne de langue externe, vous pouvez utiliser <* ... *> pour donner du code Wolfram Language pour évaluer:
Cela fonctionne également dans les cellules de langage externes:
Bien sûr, Python n'est pas Wolfram Language, donc beaucoup de choses ne fonctionnent pas:
Mais
ExternalEvaluate peut au moins renvoyer de nombreux types de données de Python, y compris des listes (en tant que
liste ), des dictionnaires (en tant
qu'association ), des images (en tant qu'image), des dates (en tant que
DateObject ), des
tableaux NumPy (en tant que
NumericArray ) et des
jeux de données pandas (en tant que
TimeSeries ,
DataSet , etc.). (
ExternalEvaluate peut également renvoyer
ExternalObject qui est fondamentalement un handle vers un objet que vous pouvez renvoyer à Python.)
Vous pouvez également utiliser directement des fonctions externes (l'ordre légèrement bizarrement nommé est essentiellement l'analogue Python de
ToCharacterCode ):
Et voici une fonction pure de Python, représentée symboliquement dans le Wolfram Language:
Appel de la langue Wolfram à partir de Python et d'autres endroits
Comment accéder à Wolfram Language? Il y a plusieurs façons. On peut l'utiliser directement dans un cahier. On peut
appeler des API qui l'exécutent dans le cloud. Ou on peut utiliser
WolframScript dans un
shell en ligne de commande . WolframScript peut fonctionner soit contre un
moteur Wolfram local, soit contre un
moteur Wolfram dans le cloud . Il vous permet de donner directement du code à exécuter:
Et cela vous permet de faire des choses comme définir des fonctions, par exemple avec du code dans un fichier:
Parallèlement à la sortie de la version 12.0, nous publions également notre première nouvelle
bibliothèque client Wolfram Language — pour Python. L'idée de base de cette bibliothèque est de permettre aux programmes Python d'appeler facilement le langage Wolfram. (Il convient de souligner que nous possédons effectivement une bibliothèque cliente en langage C depuis pas moins de 30 ans - via ce que l'on appelle maintenant
WSTP .)
Le fonctionnement d'une bibliothèque client de langues est différent selon les langues. For Python—as an interpreted language (that was actually historically informed by early Wolfram Language)—it's particularly simple. After you
set up the library , and start a session (locally or in the cloud), you can then just evaluate Wolfram Language code and get the results back in Python:
You can also directly access Wolfram Language functions (as a kind of inverse of
ExternalFunction ):
And you can directly interact with things like pandas structures, NumPy arrays, etc. In fact, you can in effect just treat the whole of the Wolfram Language like a giant library that can be accessed from Python. Or, of course, you can just use the nice, integrated Wolfram Language directly, perhaps creating external APIs if you need them.
More for the Wolfram “Super Shell”
One feature of using the Wolfram Language is that it lets you get away from having to think about the details of your computer system, and about things like files and processes. But sometimes one wants to work at a systems level. And for fairly simple operations, one can just use an operating system GUI. But what about for more complicated things? In the past I usually found myself using the
Unix shell . But for a long time now, I've instead used Wolfram Language.
It's certainly very convenient to have everything in a notebook, and it's been great to be able to programmatically use functions like
FileNames (ls),
FindList (grep),
SystemProcessData (ps),
RemoteRunProcess (ssh) and
FileSystemScan . Mais dans la version 12.0, nous ajoutons un tas de fonctions supplémentaires pour prendre en charge l'utilisation de Wolfram Language comme un «super shell».Il y a RemoteFile pour représenter symboliquement un fichier distant (avec authentification si nécessaire) - que vous pouvez immédiatement utiliser dans des fonctions comme CopyFile . Il existe FileConvert pour convertir directement des fichiers entre différents formats.Et si vous voulez vraiment plonger profondément, voici comment vous suivriez tous les paquets sur les ports 80 et 443 utilisés dans la lecture de wolfram.com :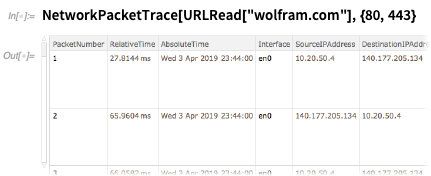
Marionnage d'un navigateur Web
Dans Wolfram Language, il est facile d'interagir depuis longtemps avec les serveurs Web, en utilisant des fonctions comme
URLExecute et
HTTPRequest , ainsi que $
Cookies , etc. Mais dans la version 12.0, nous ajoutons quelque chose de nouveau: la capacité de Wolfram Language à
contrôler un navigateur Web et à le faire faire ce que nous voulons par programmation. La chose la plus immédiate que nous pouvons faire est simplement d'obtenir une image de ce à quoi ressemble un site Web pour un navigateur Web:
Le résultat est une image que nous pouvons calculer avec:
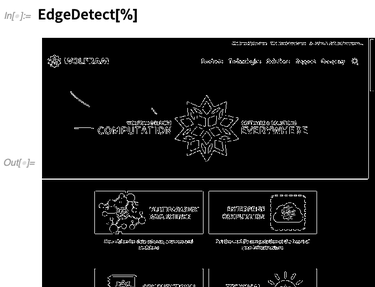
Pour faire quelque chose de plus détaillé, nous devons démarrer une session de navigateur (nous prenons actuellement en charge Firefox et Chrome):
Immédiatement, une fenêtre de navigateur vierge apparaît sur notre écran. Nous pouvons maintenant utiliser WebExecute pour ouvrir une page Web:
Maintenant que nous avons ouvert la page, nous pouvons exécuter de nombreuses commandes. Cela clique sur le premier lien hypertexte contenant le texte «Programming Lab»:
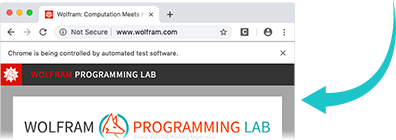
Cela renvoie le titre de la page que nous avons atteinte:
Vous pouvez taper dans des champs, exécuter JavaScript et faire essentiellement par programmation tout ce que vous pourriez faire à la main avec un navigateur Web. Il va sans dire que nous utilisons une version de cette technologie depuis des années au sein de notre entreprise pour tester tous nos différents sites Web et services Web. Mais maintenant, dans la version 12.0, nous rendons une version simplifiée généralement disponible.
Pour chaque ordinateur à usage général dans le monde aujourd'hui, il y a probablement 10 fois plus de
microcontrôleurs - exécutant des calculs spécifiques sans aucun système d'exploitation général. Un microcontrôleur peut coûter de quelques cents à quelques dollars, et dans quelque chose comme une voiture de milieu de gamme, il pourrait y en avoir 30.
Dans la version 12.0, nous introduisons un
kit de microcontrôleur pour le langage Wolfram, qui vous permet de fournir des spécifications symboliques à partir desquelles il génère et déploie automatiquement du code pour s'exécuter de manière autonome dans les microcontrôleurs. Dans la configuration typique, un microcontrôleur effectue en continu des calculs sur les données provenant des capteurs et envoie en temps réel des signaux aux actionneurs. Les types de calculs les plus courants sont effectivement ceux de la théorie du contrôle et du traitement du signal.
Depuis longtemps, nous bénéficions d'un large soutien pour la
théorie du contrôle et
le traitement du signal directement dans le langage Wolfram. Mais maintenant, ce qui est possible avec le kit de microcontrôleur est de prendre ce qui est spécifié dans la langue et de le télécharger en tant que code intégré dans un microcontrôleur autonome qui peut être
déployé n'importe où (dans les appareils, l'IoT, les appliances, etc.).
À titre d'exemple, voici comment générer une représentation symbolique d'un filtre de traitement de signal analogique:
Nous pouvons utiliser ce filtre directement dans le Wolfram Language - disons en utilisant
RecurrenceFilter pour l'appliquer à un signal audio. Nous pouvons également faire des choses comme tracer sa réponse en fréquence:
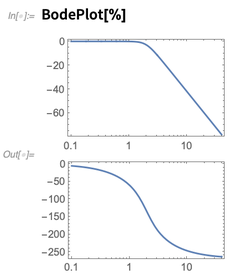
Pour déployer le filtre dans un microcontrôleur, nous devons d'abord dériver de cette représentation en temps continu une approximation en temps discret qui peut être exécutée en boucle serrée (ici, toutes les 0,1 secondes) dans le microcontrôleur:
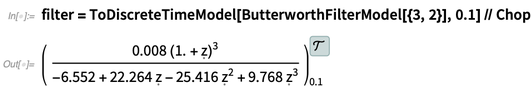
Nous sommes maintenant prêts à utiliser le kit de microcontrôleur pour le déployer réellement sur un microcontrôleur. Le kit prend en charge plus d'une centaine de types de microcontrôleurs différents. Voici comment nous pourrions déployer le filtre sur un
Arduino Uno que nous avons connecté à un port série sur notre ordinateur:
Le microcontrôleur EmbedCode fonctionne en générant le code source approprié de type C, en le compilant pour l'architecture de microcontrôleur que vous souhaitez, puis en le déployant réellement sur le microcontrôleur via son soi-disant programmeur. Voici le code source réel qui a été généré dans ce cas particulier:
Alors maintenant, nous avons une chose comme celle-ci qui exécute notre
filtre Butterworth , que nous pouvons utiliser n'importe où:
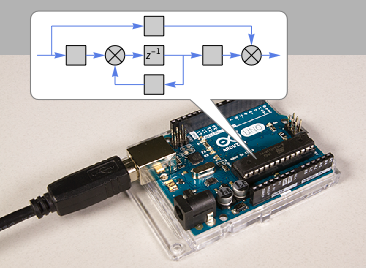
Si nous voulons vérifier ce qu'il fait, nous pouvons toujours le reconnecter au Wolfram Language en utilisant
DeviceOpen pour ouvrir son
port série et lire et écrire à partir de celui-ci.
Quelle est la relation entre Wolfram Language et les jeux vidéo? Au fil des ans, le Wolfram Language a été utilisé en coulisse dans de
nombreux aspects du développement de jeux (simulation de stratégies, création de géométries, analyse des résultats, etc.). Mais depuis quelque temps, nous travaillons sur un lien plus étroit entre Wolfram Language et l'
environnement de jeu Unity , et dans la version 12.0, nous publions une première version de ce lien.
Le schéma de base consiste à faire fonctionner Unity avec le Wolfram Language, puis à configurer une communication bidirectionnelle, permettant l'échange d'objets et de commandes. La plomberie sous le capot est assez complexe, mais le résultat est une belle fusion des forces de Wolfram Language et Unity.
Cela établit le lien, puis démarre un nouveau projet dans Unity:
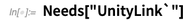
Créez maintenant une forme complexe:
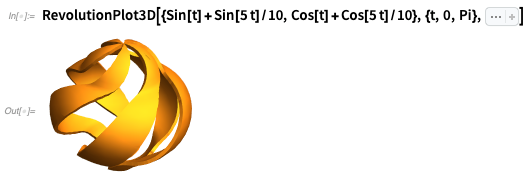
Ensuite, il suffit d'une seule commande pour mettre cela dans le jeu Unity en tant qu'objet appelé "
thingoid ":
Dans le Wolfram Language, il y a une représentation symbolique de l'objet, et UnityLink fournit désormais des centaines de fonctions pour manipuler de tels objets, en conservant toujours des versions à la fois dans Unity et dans le Wolfram Language.
Il est très puissant que l'on puisse prendre des choses du Wolfram Language et les mettre immédiatement dans Unity - que ce soit la
géométrie , les
images , l'
audio , le
géo terrain ,
les structures moléculaires ,
l'anatomie 3D ou autre. Il est également très puissant que de telles choses puissent ensuite être manipulées dans le jeu Unity, soit par des choses comme la physique du jeu, soit par l'action de l'utilisateur. (Finalement, on peut s'attendre à avoir une fonctionnalité de type
Manipuler , dans laquelle les contrôles ne sont pas seulement des curseurs et des choses, mais des éléments de jeu complexes.)
Nous avons fait des expériences pour mettre du contenu généré par Wolfram Language dans la réalité virtuelle depuis le début des années 1990. Mais dans les temps modernes, Unity est devenu une sorte de norme de facto pour la mise en place d'environnements VR / AR - et avec UnityLink, il est désormais simple de mettre régulièrement des éléments de Wolfram Language dans n'importe quel environnement XR moderne.
On peut utiliser Wolfram Language pour préparer du matériel pour les jeux Unity, mais dans un jeu Unity, UnityLink permet également simplement d'insérer du code Wolfram Language qui peut être exécuté pendant un jeu sur une machine locale ou via une API dans
Wolfram Cloud . Et, entre autres choses, il est facile de mettre des crochets dans un jeu afin que le jeu puisse envoyer de la «télémétrie» (disons au
Wolfram Data Drop ) pour analyse dans le Wolfram Language. (Il est également possible de scénariser le jeu - ce qui est, par exemple, très utile pour les tests de jeu.)
L'écriture de jeux est une affaire complexe. Mais UnityLink propose une nouvelle approche intéressante qui devrait faciliter le prototypage de toutes sortes de jeux et apprendre les idées de développement de jeux. Une des raisons à cela est qu'il permet effectivement d'écrire un jeu à un niveau supérieur en utilisant des constructions symboliques dans le Wolfram Language. Mais une autre raison est qu'elle permet au processus de développement de se faire de manière incrémentielle dans un cahier, et d'expliquer et de documenter chaque étape du processus. Par exemple, voici ce qui revient à un
essai informatique décrivant le développement d'un «
jeu de piano »:
UnityLink n'est pas une chose simple: il contient plus de 600 fonctions. Mais avec ces fonctions, il est possible d'accéder à presque toutes les capacités d'Unity et de configurer à peu près n'importe quel jeu imaginable.
Pour quelque chose comme l'apprentissage par renforcement, il est essentiel d'avoir un environnement externe manipulable dans la boucle lorsque l'on fait un apprentissage automatique. Eh bien,
ServiceExecute vous permet d'activer des appareils réels (tournez le robot vers la gauche) et d'obtenir des données de capteurs (le robot est-il tombé?) Et
DeviceExecute vous permet d'appeler des API (quel est l'effet de publier ce tweet ou de faire ce commerce?).
Mais à de nombreuses fins, ce que l'on souhaite à la place, c'est d'avoir un environnement externe simulé. Et d'une certaine manière, le pur Wolfram Language le fait déjà dans une certaine mesure, par exemple en donnant accès à un riche «univers de calcul» plein de programmes et d'équations modifiables (
automates cellulaires ,
équations différentielles , ...). Et, oui, les choses dans cet univers informatique peuvent être informées par le monde réel - disons avec les propriétés réalistes des
océans , des
produits chimiques ou des
montagnes .
Mais qu'en est-il des environnements qui ressemblent davantage à ceux que les humains modernes apprennent généralement - pleins de structures d'ingénierie construites, etc.? Assez
commodément ,
SystemModel donne accès à de nombreux systèmes d'ingénierie réalistes. Et grâce à UnityLink, nous pouvons nous attendre à avoir accès à de riches simulations du monde basées sur des jeux.
Mais dans un premier temps, dans la version 12.0, nous mettons en place des connexions à certains jeux simples - en particulier à partir du
«gym» OpenAI . L'interface est similaire à ce qu'elle serait pour interagir avec le monde réel, avec le jeu accessible comme un «appareil» (après une installation appropriée parfois «open-source-douloureuse»):
On peut lire l'état du jeu:
Et nous pouvons le montrer comme une image:
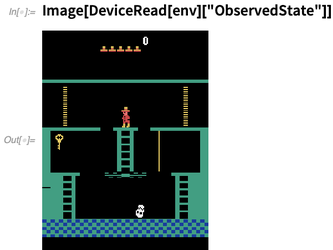
Avec un peu plus d'efforts, nous pouvons effectuer 100 actions aléatoires dans le jeu (en vérifiant toujours que nous ne sommes pas «morts»), puis afficher un graphique de l'espace des fonctionnalités des états observés du jeu:
Dans la version 11.3, nous avons commencé
notre première connexion à la blockchain . La version 12.0 ajoute de nombreuses nouvelles fonctionnalités et capacités, notamment la possibilité d'écrire sur des chaînes de blocs publiques, ainsi que de les lire. (Nous avons également notre propre chaîne de blocs
Wolfram pour les utilisateurs de Wolfram Cloud.) Nous prenons actuellement en charge les chaînes de blocs
Bitcoin ,
Ethereum et
ARK , à la fois leurs réseaux principaux et leurs réseaux de test (et, oui, nous avons nos propres nœuds se connectant directement à ces chaînes de blocs).
Dans la version 11.3, nous autorisions
la lecture brute des transactions à partir des chaînes de blocs. Dans la version 12.0, nous avons ajouté une couche d'analyse, de sorte que, par exemple, vous pouvez demander un résumé des jetons «CK» (AKA
CryptoKitties ) sur la blockchain
Ethereum :
Il est rapide de regarder toutes les transactions de jetons dans l'historique et de faire un nuage de mots de la façon dont les différents jetons ont été actifs:
Mais qu'en est-il de faire notre propre transaction? Disons que nous voulons utiliser un
guichet automatique Bitcoin (comme celui qui, bizarrement,
existe dans un magasin de bagels près de chez moi ) pour transférer de l'argent vers une adresse Bitcoin. Eh bien, nous créons d'abord nos clés de chiffrement (et nous devons nous assurer de nous souvenir de notre clé privée!):
Ensuite, nous devons prendre notre clé publique et générer une adresse Bitcoin à partir de celle-ci:
Faites un code QR à partir de cela et vous êtes prêt à vous rendre au GAB:
Mais que faire si nous voulons écrire nous-mêmes sur la blockchain? Ici, nous allons utiliser le testnet Bitcoin (donc nous ne dépensons pas d'argent réel). Cela montre une sortie d'une transaction que nous avons faite auparavant - qui comprend 0,0002 bitcoin (soit 20000 satoshi):
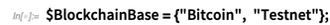
Maintenant, nous pouvons configurer une transaction qui prend cette sortie et, par exemple, envoie 8000 satoshi à chacune des deux adresses (que nous avons définies comme pour la transaction ATM):
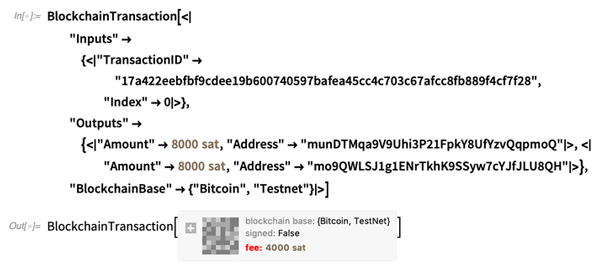
OK, alors maintenant nous avons un objet de transaction blockchain - qui offrirait des frais (affichés en rouge parce que c'est "de l'argent réel" que vous dépenserez) de toute la crypto-monnaie restante (ici 4000 satoshi) à un mineur désireux de mettre le transaction dans la blockchain. Mais avant de pouvoir soumettre cette transaction (et «dépenser l'argent»), nous devons la signer avec notre clé privée:
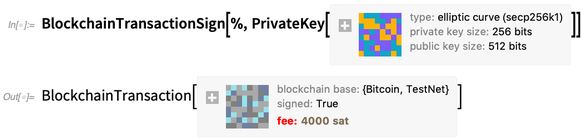
Enfin, nous appliquons simplement
BlockchainTransactionSubmit et nous avons soumis notre transaction à mettre sur la blockchain:
Voici son ID de transaction:
Si nous posons immédiatement des questions sur cette transaction, nous recevrons un message disant qu'elle n'est pas dans la blockchain:
Mais après avoir attendu quelques minutes, il est là - et il se propagera bientôt à chaque copie de la blockchain de Bitcoin testnet:
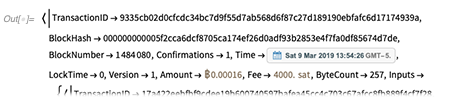
Si vous êtes prêt à dépenser de l'argent réel, vous pouvez utiliser exactement les mêmes fonctions pour effectuer une transaction sur un réseau principal. Vous pouvez également faire des choses comme acheter des CryptoKitties. Des fonctions telles que
BlockchainContractValue peuvent être utilisées pour tout contrat intelligent (pour l'instant, uniquement Ethereum) et sont configurées pour comprendre immédiatement des éléments tels que les jetons
ERC-20 et
ERC-721 .
Le traitement des chaînes de blocs implique beaucoup de cryptographie, dont certaines sont nouvelles dans la version 12.0 (notamment la gestion des courbes elliptiques). Mais dans la version 12.0, nous étendons également nos fonctions cryptographiques non blockchain. Par exemple, nous avons maintenant des fonctions pour traiter directement
les signatures numériques . Cela crée une signature numérique à l'aide de la clé privée ci-dessus:
Désormais, n'importe qui peut vérifier le message à l'aide de la clé publique correspondante:
Dans la version 12.0, nous avons ajouté plusieurs nouveaux types de hachages pour la fonction de
hachage , en particulier pour prendre en charge diverses crypto-monnaies. Nous avons également ajouté des moyens de générer et de vérifier les
clés dérivées . Commencez à partir de n'importe quel mot de passe, et
GenerateDerivedKey "gonflera" quelque chose de plus long (pour être plus sûr, vous devez ajouter "
salt "):
Voici une version de la clé dérivée, adaptée à une utilisation dans divers schémas d'authentification:
Connexion aux flux de données financières
La base de
connaissances Wolfram contient toutes sortes de
données financières . Il y a généralement une
entité financière (comme un stock), puis une propriété (comme le prix). Voici l'historique quotidien complet du cours des actions d'Apple (il est très impressionnant qu'il soit le meilleur sur une échelle logarithmique):
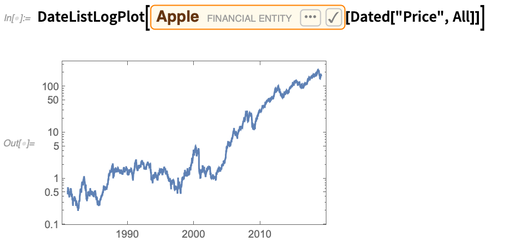
Mais bien que les données financières dans la base de connaissances Wolfram, et disponibles en standard dans la langue Wolfram, soient mises à jour en continu, ce n'est pas en temps réel (généralement retardé de 15 minutes), et il n'a pas tous les détails que de nombreux commerçants financiers utilisent. Pour une utilisation financière sérieuse, cependant, nous avons développé
Wolfram Finance Platform . Et maintenant, dans la version 12.0, il a un accès direct aux flux de données financières de Bloomberg et Reuters.
La façon dont nous concevons Wolfram Language, le cadre des connexions à Bloomberg et Reuters, est toujours disponible dans la langue - mais il n'est activé que si vous avez Wolfram Finance Platform, ainsi que les abonnements Bloomberg ou Reuters appropriés. Mais en supposant que vous les ayez, voici à quoi cela ressemble de se connecter au service
Bloomberg Terminal :
Tous les instruments financiers gérés par le terminal Bloomberg deviennent désormais disponibles en tant qu'entités dans la langue Wolfram:
Maintenant, nous pouvons demander les propriétés de cette entité:
Au total, plus de 60 000 propriétés sont accessibles depuis le terminal Bloomberg:
Voici 5 exemples aléatoires (oui, ils sont assez détaillés; ce sont des noms Bloomberg, pas les nôtres):
Nous prenons en charge le service Bloomberg Terminal, le service
Bloomberg Data License et le service
Reuters Elektron . Une chose sophistiquée que l'on peut maintenant faire est de configurer une tâche continue pour recevoir des données de manière asynchrone et d'appeler une «
fonction de gestionnaire » chaque fois qu'une nouvelle donnée arrive:
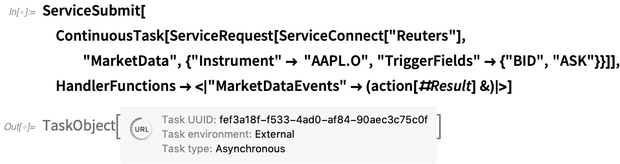
Génie logiciel et mises à jour de plate-forme
J'ai parlé de beaucoup de nouvelles fonctions et de nouvelles fonctionnalités dans le Wolfram Language. Mais qu'en est-il de l'infrastructure sous-jacente de Wolfram Language? Eh bien, nous avons travaillé dur aussi. Par exemple, entre la version 11.3 et la version 12.0, nous avons réussi à corriger près de 8 000 bogues signalés. Nous avons également rendu beaucoup de choses plus rapides et plus robustes. Et en général, nous avons resserré l'ingénierie logicielle du système, par exemple en réduisant la taille de téléchargement initiale de près de 10% (malgré toutes les fonctionnalités qui ont été ajoutées). (Nous avons également amélioré la
prélecture prédictive
des éléments de la base
de connaissances à partir du cloud. Ainsi, lorsque vous avez besoin de données similaires, il est plus probable qu'elles soient déjà mises en cache sur votre ordinateur.)
C'est une caractéristique de longue date du paysage informatique que les systèmes d'exploitation sont constamment mis à jour - et pour profiter de leurs dernières fonctionnalités, les applications doivent également être mises à jour. Nous travaillons depuis plusieurs années sur une mise à jour majeure de notre interface pour ordinateur portable Mac - qui est enfin prête dans la version 12.0. Dans le cadre de la mise à jour, nous avons réécrit et restructuré de grandes quantités de code qui ont été développées et peaufinées sur plus de 20 ans, mais le résultat est que dans la version 12.0, tout ce qui concerne notre système sur Mac est entièrement 64 bits, et utilise les dernières
API Cocoa . Cela signifie que le frontal du portable est beaucoup plus rapide - et peut également dépasser la limite de mémoire précédente de 2 Go.
Il existe également une mise à jour de la plate-forme sous Linux, où l'interface du notebook prend désormais entièrement en charge
Qt 5 , ce qui permet à toutes les opérations de rendu de se dérouler «sans tête», sans aucun serveur X, ce qui rationalise considérablement le déploiement de
Wolfram Engine dans le cloud. (La version 12.0 n'a pas encore de prise en charge haute résolution pour Windows, mais cela arrivera très bientôt.)
Le développement de
Wolfram Cloud est en quelque sorte distinct du développement des applications Wolfram Language et
Wolfram Desktop (bien que pour la compatibilité interne, nous publions la version 12.0 en même temps dans les deux environnements). Mais au cours de l'année écoulée depuis la sortie de la version 11.3, des progrès spectaculaires ont été accomplis dans Wolfram Cloud.
Les avancées dans les ordinateurs portables cloud sont particulièrement remarquables - prenant en charge davantage d'éléments d'interface (y compris certains, comme les sites Web et les vidéos intégrés, qui ne sont même pas encore disponibles dans les ordinateurs de bureau), ainsi que la robustesse et la vitesse considérablement accrues. (Faire fonctionner l'ensemble de notre interface de bloc-notes dans un navigateur Web n'est pas une mince affaire d'ingénierie logicielle, et dans la version 12.0, il existe des stratégies assez sophistiquées pour des choses comme le maintien de caches cohérents à chargement rapide, ainsi que des représentations DOM symboliques complètes.)
Dans la version 12.0, il n'y a maintenant qu'un simple élément de menu (Fichier> Publier dans le cloud ...) pour publier n'importe quel bloc-notes dans le cloud. Et une fois que le cahier est publié, n'importe qui dans le monde peut interagir avec lui - ainsi que faire sa propre copie afin de pouvoir le modifier.
Il est intéressant de voir à
quel point le cloud est entré dans ce qui peut être fait dans Wolfram Language. En plus de toute l'intégration transparente de la base de connaissances du cloud et de la possibilité d'atteindre des éléments tels que les chaînes de blocs, il existe également des fonctionnalités telles que
Envoyer à ... envoyer n'importe quel bloc-notes par e-mail, en utilisant le cloud s'il n'y a pas de connexion directe au serveur de messagerie disponible.
Et bien d'autres ...
Même si cela a été un long morceau, il n'est même pas près de raconter toute l'histoire des nouveautés de la version 12.0. Avec le reste de notre équipe, je travaille très dur sur la version 12.0 depuis longtemps - mais c'est toujours excitant de voir à quel point il y en a réellement.
Mais ce qui est essentiel (et beaucoup de travail à accomplir!), C'est que tout ce que nous avons ajouté est soigneusement conçu pour s'adapter de manière cohérente à ce qui existe déjà. Depuis la toute première version il y a plus de 30 ans de ce qui est maintenant le Wolfram Language, nous avons suivi les mêmes principes de base - et cela fait partie de ce qui nous a permis de développer le système de manière spectaculaire tout en conservant une compatibilité à long terme.
Il est toujours difficile de décider exactement ce qu'il faut prioriser pour chaque nouvelle version, mais je suis très satisfait des choix que nous avons faits pour la version 12.0. J'ai donné de nombreuses conférences au cours de l'année écoulée et j'ai été très frappé par la fréquence à laquelle j'ai pu dire des choses qui se présentent: «Eh bien, il se trouve que cela fera partie de la version 12.0! "
Personnellement, j'utilise les versions préliminaires internes de la version 12.0 depuis près d'un an, et j'en suis venu à tenir pour acquis bon nombre de ses nouvelles capacités - et à les utiliser et à en profiter beaucoup. C'est donc un grand plaisir que nous ayons aujourd'hui la version finale 12.0 - avec toutes ces nouvelles capacités officiellement, prêtes à être utilisées par tout le monde ...