Présentation
Cet article est la suite d'une
série d'articles décrivant les algorithmes sous-jacents.
Synet est un framework pour lancer des réseaux neuronaux pré-entraînés sur le CPU.
Si vous regardez la distribution du temps processeur consacré à la propagation directe du signal dans les réseaux de neurones, il s'avère que plus de 90% du temps est souvent passé dans les couches convolutives. Par conséquent, si nous voulons obtenir un algorithme rapide pour un réseau de neurones, nous avons d'abord besoin d'un algorithme rapide pour une couche convolutionnelle. Dans cet article, je souhaite décrire les méthodes d'optimisation de la propagation directe du signal dans une couche convolutionnelle. Et je veux commencer par les méthodes les plus utilisées basées sur la multiplication matricielle. Je vais essayer de garder la présentation sous la forme la plus accessible afin que l'article soit intéressant non seulement pour les spécialistes (ils savent déjà tout à ce sujet), mais aussi pour un cercle plus large de lecteurs. Je ne prétends pas être un examen complet, donc tous les commentaires et ajouts sont les bienvenus.
Options de couche de convolution
Je voudrais commencer la description par une description des paramètres qui se trouvent dans la couche convolutionnelle. Les experts peuvent ignorer cette section en toute sécurité.
Tailles d'image d'entrée et de sortie
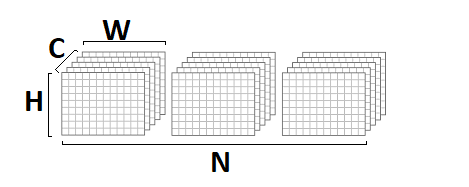
Tout d'abord, une couche convolutionnelle est caractérisée par une image d'entrée et une image de sortie, qui sont caractérisées par les paramètres suivants:

- srcC / dstC - le nombre de canaux dans l'image d'entrée et de sortie. Notation alternative: C / D.
- srcH / dstH - hauteur de l'image d'entrée et de sortie. Autre désignation: H.
- srcW / dstW - largeur de l'image d'entrée et de sortie. Désignation alternative: W.
- lot - le nombre d'images d'entrée (sortie) - la couche peut traiter un lot entier d'images à la fois. Désignation alternative: N.
Tailles de noyau de convolution
L'opération de convolution est intrinsèquement une somme pondérée d'un certain voisinage d'un point donné dans l'image. La taille du noyau de convolution - caractérise la taille de ce voisinage et est décrite par deux paramètres:

- kernelY est la hauteur du noyau de convolution. Désignation alternative: Y.
- kernelX est la largeur du noyau de convolution. Désignation alternative: X.
Les circonvolutions les plus courantes avec une taille de noyau de
1x1 et
3x3 . Les tailles
5x5 et
7x7 sont beaucoup moins courantes. De grandes tailles de convolution, ainsi que des convolutions avec un noyau autre que carré, sont également parfois trouvées, mais cela est plus exotique.
Étape de convolution
Un autre paramètre important est l'étape de convolution:

- strideY est l'étape de convolution verticale.
- strideX - étape de convolution horizontale.
Si le pas est différent de
1x1 , par exemple -
2x2 , alors l'image de sortie sera moitié moins (la convolution sera calculée uniquement au voisinage des points pairs).
Étirement de la convolution
Le noyau de convolution peut être étiré (augmenter la taille effective de la fenêtre, tout en maintenant le nombre d'opérations) en utilisant les paramètres suivants:
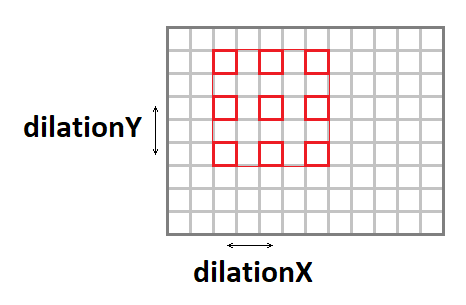
- dilatation Y - étirement vertical de la convolution.
- dilationX - étirement horizontal de la convolution.
Il est à noter que les cas avec des étirements autres que
1x1 sont assez rares (je n'ai jamais rencontré une telle chose dans ma carrière).
Image d'entrée de remplissage
Si vous appliquez une convolution avec une fenêtre qui est différente d'une seule à l'image, alors l'image de sortie sera inférieure de la quantité de
noyau - 1 . Le paquet, pour ainsi dire, «mange» les bords. Pour conserver la taille de l'image, l'image d'entrée est souvent rembourrée sur les bords avec des zéros. Quatre autres paramètres en sont responsables:

- padY / padX - rembourrage vertical et horizontal avant.
- padH / padW - rembourrage arrière vertical et horizontal.
Groupes de canaux
En règle générale, chaque canal de sortie est la somme des convolutions sur tous les canaux d'entrée. Mais ce n'est pas toujours le cas. Il est possible de diviser les canaux d'entrée et de sortie en groupes, la sommation est effectuée uniquement au sein des groupes:

- groupe - le nombre de groupes.
En pratique, les situations avec
groupe = 1 et
groupe = srcC = dstC , ce que l'on appelle la
convolution en profondeur, sont le plus souvent rencontrées.
Fonction de déplacement et d'activation
Bien que formellement, la fonction de déplacement et d'activation ne soit pas incluse dans la convolution, mais très souvent ces deux opérations suivent la couche convolutionnelle, pourquoi elles y sont généralement également incluses. Compte tenu de la diversité des fonctions d'activation possibles et de leurs paramètres, je ne les décrirai pas ici en détail.
Implémentation de base de l'algorithme
Pour commencer, je voudrais donner une implémentation de base de l'algorithme:
float relu(float value) { return value > 0 ? return value : 0; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int b = 0; b < batch; ++b) { for (int g = 0; g < group; ++g) { for (int dc = 0; dc < dstC / group; ++dc) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { float sum = 0; for (int sc = 0; sc < srcC / group; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) sum += src[((b * srcC + sc)*srcH + sy)*srcW + sx] * weight[((dc * srcC / group + sc)*kernelY + ky)*kernelX + kx]; } } } dst[((b * dstC + dc)*dstH + dy)*dstW + dx] = relu(sum + bias[dc]); } } } } } }
Dans cette implémentation, j'ai supposé que l'image d'entrée et de sortie était au format
NCHW :
les poids de convolution sont stockés au format
DCYX , et notre fonction d'activation est
ReLU . Dans le cas général, ce n'est pas le cas, mais pour la mise en œuvre de base, de telles hypothèses sont tout à fait appropriées - vous devez partir de quelque chose.
Nous avons 8 cycles imbriqués et le nombre total d'opérations:
batch * kernelY * kernelX * srcC * dstH * dstW * dstC / group * 2,
tandis que la quantité de données dans l'entrée:
batch * srcC * srcH * srcW,
et l'image de sortie:
batch * dstC * dstH * dstW,
et le nombre de poids:
kernelY * kernelX * srcC * dstC / group.
Si le
groupe << srcC (le nombre de groupes est beaucoup plus petit que le nombre de canaux), ainsi qu'avec des paramètres suffisamment grands
srcC ,
srcH ,
srcW et
dstC , nous obtenons un problème de calcul classique lorsque le nombre de calculs dépasse considérablement la quantité de données d'entrée et de sortie. C'est-à-dire une opération de convolution avec une mise en œuvre appropriée doit reposer sur les ressources informatiques du processeur, et non sur la bande passante mémoire. Il ne reste plus qu'à retrouver cette implémentation.
Réduction du problème à la multiplication matricielle
L'opération principale de la convolution est d'obtenir une somme pondérée, et les poids sont les mêmes pour tous les points de l'image de sortie. Si vous réorganisez l'image d'entrée comme suit:
void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int sc = 0; sc < srcC; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[((b * srcC + sc)*srcH + sy)*srcW + sx]; else *buf++ = 0; } } } } } }
Ensuite, nous passerons du format
srcC - srcH - srcW nous passerons au format
srcC - kernelY - kernelX - dstH - dstW . La figure ci-dessous montre comment l'image est convertie avec un noyau de remplissage
1 et
3x3 :
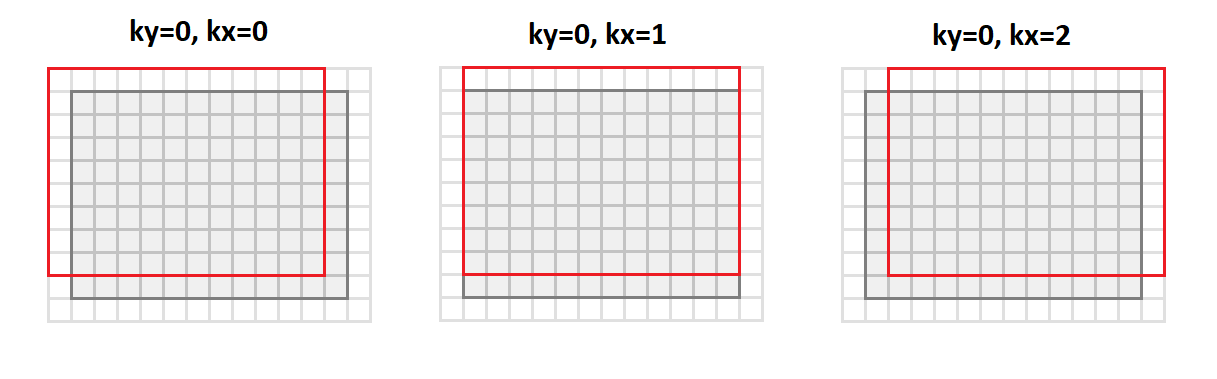
Dans ce cas, tous les points du voisinage d'image requis pour l'opération de convolution sont alignés le long des colonnes de la matrice résultante (d'où son nom - image en colonnes).
La nouvelle représentation de l'image d'entrée est intéressante en ce que maintenant l'opération de convolution en nous est réduite à la multiplication matricielle:
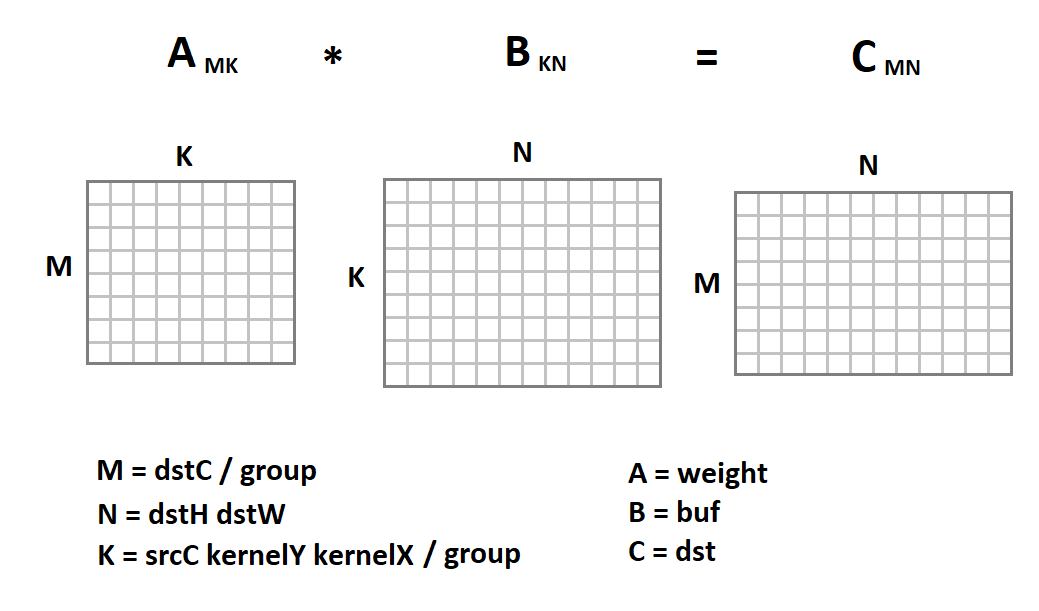
Maintenant, le code de convolution ressemblera à ceci:
void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) { for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstC / group; int N = dstH * dstW; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, weight + M * K * g, K, 0, buf + N * K * g, N, dst + M * N * g, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } }
Ici, l'implémentation triviale de la multiplication matricielle n'est donnée qu'à titre d'exemple. Nous pouvons le remplacer par n'importe quelle autre implémentation. Heureusement, la multiplication matricielle est une opération de longue date qui a déjà été implémentée dans de nombreuses bibliothèques avec une très grande efficacité (jusqu'à 90% des performances CPU théoriquement possibles). Au sujet de la façon dont cette efficacité est atteinte, j'ai même un
article séparé .
Utilisation de la multiplication matricielle pour le format NHWC
Avec le format
NCHW ,
NHWC est souvent utilisé dans l'apprentissage automatique:

Par exemple, notez que
NHWC est le format natif
Tensorflow .
Il est à noter que pour ce format, l'opération de convolution peut également conduire à une multiplication matricielle. Pour ce faire, à partir du format
srcH - srcW - srcC, nous traduisons l'image originale au format
dstH - dstW - kernelY - kernelX - srcC en utilisant la fonction
im2row :
void im2row(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int g = 0; g < group; ++g) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; for (int sc = 0; sc < srcC; ++sc) { if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[(sy * srcW + sx)*srcC + sc]; else *buf++ = 0; } } } } } src += srcC / group; } }
De plus, tous les points du voisinage d'image qui sont requis pour l'opération de convolution sont alignés le long des lignes de la matrice résultante (d'où son nom - image
sur la ligne s). Nous devons également changer le format de stockage des échelles de convolution du format
DCYX au format
YXCD . Maintenant, nous pouvons appliquer la multiplication matricielle:

Contrairement au format
NCHW , nous multiplions la matrice d'image par la matrice de poids, et non l'inverse. Voici un code de fonction de convolution:
void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstH * dstW; int N = dstC / group; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2row(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, group, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, buf + M * K * g, K * group, 0, weight + N * g, dstC, dst + N * g, dstC)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } }
Avantages et inconvénients de la méthode
Dès le début, je voudrais énumérer les avantages de cette approche:
- Cette méthode a une implémentation très simple. Ce n'est pas pour rien qu'il est utilisé dans presque toutes les bibliothèques que je connais.
- L'efficacité de la méthode dans de nombreux cas est très élevée: à partir d'unités de pourcentage dans la version de base, nous atteignons plus de 80% du maximum théorique.
- L'approche est universelle - nous avons un code pour tous les paramètres possibles de la couche convolutionnelle (et ils sont nombreux!). Par conséquent, cette méthode fonctionne souvent dans les cas où des approches plus efficaces (et donc plus spécialisées) ont des limites.
- L'approche fonctionne pour les principaux formats de tenseurs d'images - NCHW et NHWC .
Maintenant sur les inconvénients:
- Malheureusement, la multiplication matricielle standard est efficace à condition que les valeurs des paramètres M, N, K soient suffisamment grandes et, en outre, qu'elles soient approximativement du même ordre de grandeur (l'efficacité est basée sur le fait que le nombre de calculs requis est ~ O (N ^ 3) , et le débit requis capacité de mémoire ~ O (N ^ 2) ). Par conséquent, si l'un des paramètres M, N, K est petit, l'efficacité de la méthode diminue fortement.
- La méthode nécessite la conversion des données d'entrée. Et c'est loin d'être une opération gratuite. Elle ne peut être négligée que si K est assez grand. Et si l'on tient compte du fait qu'à l'intérieur de la multiplication matricielle standard, il y a encore une transformation interne des données d'entrée, la situation devient encore plus triste.
- Basé sur le fait que K = srcC * kernelY * kernelX / group , l'efficacité de la méthode est particulièrement faible pour les couches convolutives d'entrée. Et pour la convolution en profondeur, la méthode matricielle perd généralement à la mise en œuvre triviale.
- Le procédé nécessite un traitement supplémentaire des données de sortie pour l'opération de décalage et le calcul de la fonction d'activation.
- Il existe des méthodes mathématiques plus efficaces pour calculer la convolution, qui nécessitent moins d'opérations.
Conclusions
La méthode de calcul de la convolution basée sur la multiplication matricielle est simple à mettre en œuvre et a une grande efficacité. Malheureusement, ce n'est pas universel. Pour un certain nombre de cas particuliers, il existe des approches plus rapides, dont je voudrais reporter la description pour les prochains articles de cette
série . En attente de commentaires et de commentaires des lecteurs. J'espère que vous étiez intéressé!
PS Cette approche et d'autres sont implémentées par moi dans le
cadre de convolution dans le cadre de la bibliothèque
Simd .
Ce cadre sous-tend
Synet , un cadre pour exécuter des réseaux de neurones pré-formés sur le CPU.