Préface
Il n'y a pas si longtemps, je devais travailler à simplifier la chaîne polygonale (un
processus qui permet de réduire le nombre de points de polyligne ). En général, ce type de tâche est très courant lors du traitement de graphiques vectoriels et lors de la création de cartes. À titre d'exemple, nous pouvons prendre une chaîne dont plusieurs points tombent dans le même pixel - il est évident que tous ces points peuvent être simplifiés en un seul. Il y a quelque temps, je ne savais pratiquement rien à ce sujet du mot «complètement», et j'ai donc dû rapidement remplir les connaissances nécessaires sur ce sujet. Mais quelle a été ma surprise quand je n'ai pas trouvé suffisamment de manuels complets sur Internet sur Internet ... J'ai dû chercher des extraits de sources complètement différentes et, après l'analyse, tout intégrer dans une vue d'ensemble. Pour être honnête, l'occupation n'est pas des plus agréables. Par conséquent, je voudrais écrire une série d'articles sur les algorithmes de simplification de chaîne polygonale. Je viens de décider de commencer avec l'algorithme Douglas-Pecker le plus populaire.
La description
L'algorithme définit la polyligne initiale et la distance maximale (ε), qui peut être entre les polylignes originales et simplifiées (c'est-à-dire la distance maximale entre les points de l'original et la section la plus proche de la polyligne résultante). L'algorithme divise récursivement la polyligne. L'entrée de l'algorithme est les coordonnées de tous les points entre le premier et le dernier, y compris eux, ainsi que la valeur de ε. Les premier et dernier points restent inchangés. Après cela, l'algorithme trouve le point le plus éloigné du segment composé du premier et du dernier (
l'algorithme de recherche est la distance du point au segment ). Si le point est situé à une distance inférieure à ε, tous les points qui n'ont pas encore été marqués pour la conservation peuvent être éjectés de l'ensemble, et la ligne droite résultante lisse la courbe avec une précision d'au moins ε. Si cette distance est supérieure à ε, alors l'algorithme s'appelle récursivement sur l'ensemble du point de départ au donné et du donné aux points d'arrivée.
Il convient de noter que l'algorithme Douglas-Pecker ne conserve pas la topologie au cours de ses travaux. Cela signifie qu'en conséquence, nous pouvons obtenir une ligne avec des auto-intersections. À titre d'exemple illustratif, prenez une polyligne avec l'ensemble de points suivant: [{1; 5}, {2; 3}, {5; 1}, {6; 4}, {9; 6}, {11; 4}, {13; 3}, {14; 2}, {18; 5}] et regardez le processus de simplification pour différentes valeurs de ε:
La polyligne d'origine de l'ensemble de points présenté:

Polyligne avec ε égal à 0,5:
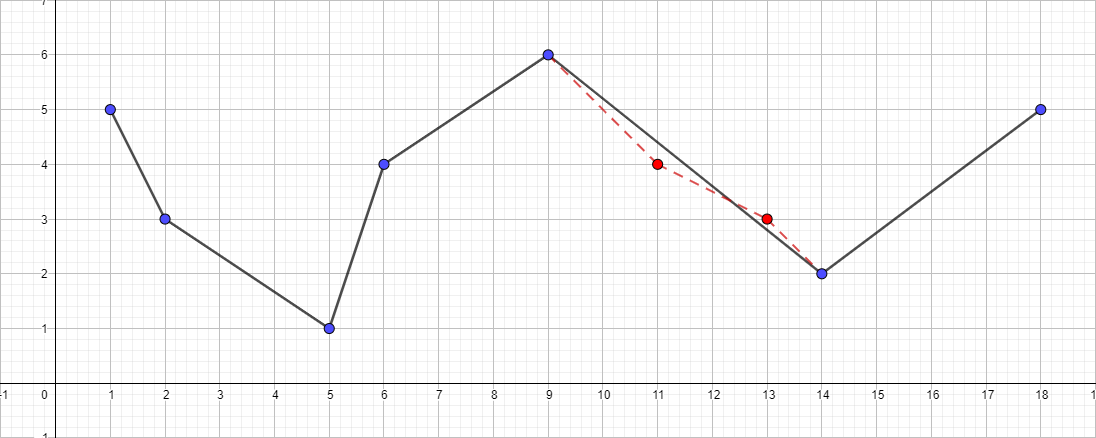
Une polyligne avec ε égal à 1:

Polyligne avec ε égal à 1,5:
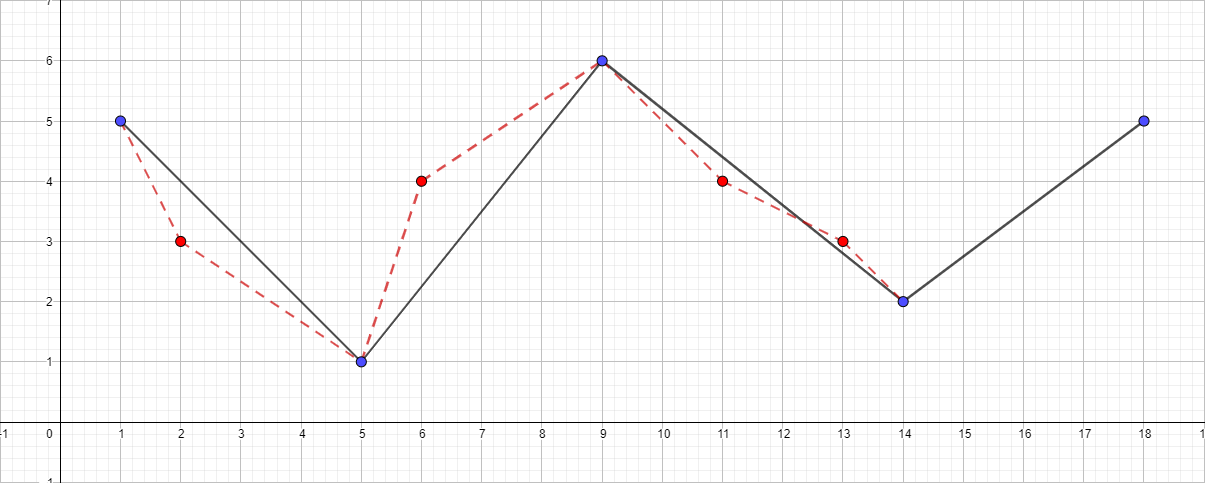
Vous pouvez continuer à augmenter la distance maximale et visualiser l'algorithme, mais, je pense, le point principal après ces exemples est devenu clair.
Implémentation
C ++ a été choisi comme langage de programmation pour l'implémentation de l'algorithme, le code source complet de l'algorithme que vous pouvez voir
ici . Et maintenant directement à l'implémentation elle-même:
#define X_COORDINATE 0 #define Y_COORDINATE 1 template<typename T> using point_t = std::pair<T, T>; template<typename T> using line_segment_t = std::pair<point_t<T>, point_t<T>>; template<typename T> using points_t = std::vector<point_t<T>>; template<typename CoordinateType> double get_distance_between_point_and_line_segment(const line_segment_t<CoordinateType>& line_segment, const point_t<CoordinateType>& point) noexcept { const CoordinateType x = std::get<X_COORDINATE>(point); const CoordinateType y = std::get<Y_COORDINATE>(point); const CoordinateType x1 = std::get<X_COORDINATE>(line_segment.first); const CoordinateType y1 = std::get<Y_COORDINATE>(line_segment.first); const CoordinateType x2 = std::get<X_COORDINATE>(line_segment.second); const CoordinateType y2 = std::get<Y_COORDINATE>(line_segment.second); const double double_area = abs((y2-y1)*x - (x2-x1)*y + x2*y1 - y2*x1); const double line_segment_length = sqrt(pow((x2-x1), 2) + pow((y2-y1), 2)); if (line_segment_length != 0.0) return double_area / line_segment_length; else return 0.0; } template<typename CoordinateType> void simplify_points(const points_t<CoordinateType>& src_points, points_t<CoordinateType>& dest_points, double tolerance, std::size_t begin, std::size_t end) { if (begin + 1 == end) return; double max_distance = -1.0; std::size_t max_index = 0; for (std::size_t i = begin + 1; i < end; i++) { const point_t<CoordinateType>& cur_point = src_points.at(i); const point_t<CoordinateType>& start_point = src_points.at(begin); const point_t<CoordinateType>& end_point = src_points.at(end); const double distance = get_distance_between_point_and_line_segment({ start_point, end_point }, cur_point); if (distance > max_distance) { max_distance = distance; max_index = i; } } if (max_distance > tolerance) { simplify_points(src_points, dest_points, tolerance, begin, max_index); dest_points.push_back(src_points.at(max_index)); simplify_points(src_points, dest_points, tolerance, max_index, end); } } template< typename CoordinateType, typename = std::enable_if<std::is_integral<CoordinateType>::value || std::is_floating_point<CoordinateType>::value>::type> points_t<CoordinateType> duglas_peucker(const points_t<CoordinateType>& src_points, double tolerance) noexcept { if (tolerance <= 0) return src_points; points_t<CoordinateType> dest_points{}; dest_points.push_back(src_points.front()); simplify_points(src_points, dest_points, tolerance, 0, src_points.size() - 1); dest_points.push_back(src_points.back()); return dest_points; }
Eh bien, en fait, l'utilisation de l'algorithme lui-même:
int main() { points_t<int> source_points{ { 1, 5 }, { 2, 3 }, { 5, 1 }, { 6, 4 }, { 9, 6 }, { 11, 4 }, { 13, 3 }, { 14, 2 }, { 18, 5 } }; points_t<int> simplify_points = duglas_peucker(source_points, 1); return EXIT_SUCCESS; }
Exemple d'exécution d'algorithme
En entrée, nous prenons un ensemble antérieur de points connus [{1; 5}, {2; 3}, {5; 1}, {6; 4}, {9; 6}, {11; 4}, {13; 3}, {14; 2}, {18; 5}] et ε égal à 1:
- Trouvez le point le plus éloigné du segment {1; 5} - {18; 5}, ce point sera le point {5; 1}.
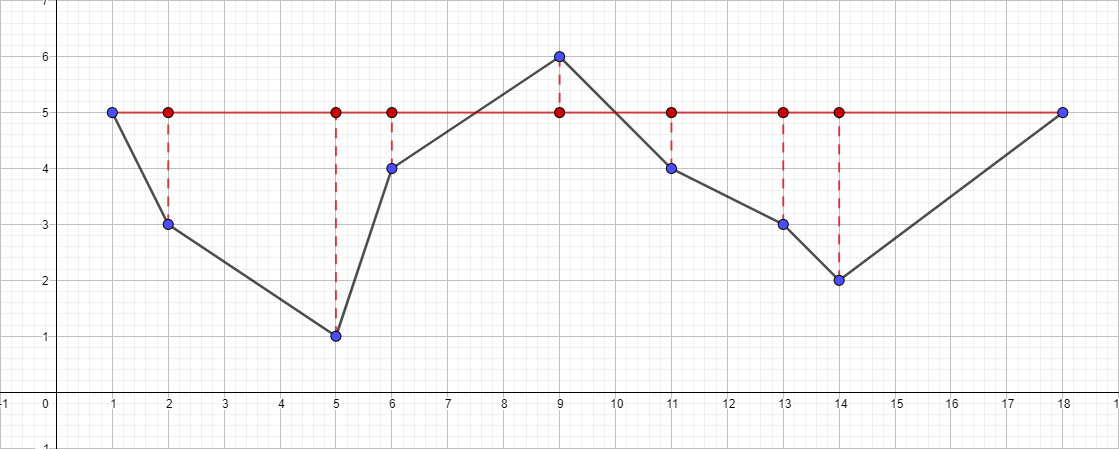
- Vérifiez sa distance au segment {1; 5} - {18; 5}. Il s'avère être supérieur à 1, ce qui signifie que nous l'ajoutons à la polyligne résultante.
- Exécutez récursivement l'algorithme pour le segment {1; 5} - {5; 1} et trouvez le point le plus éloigné de ce segment. Ce point est {2; 3}.
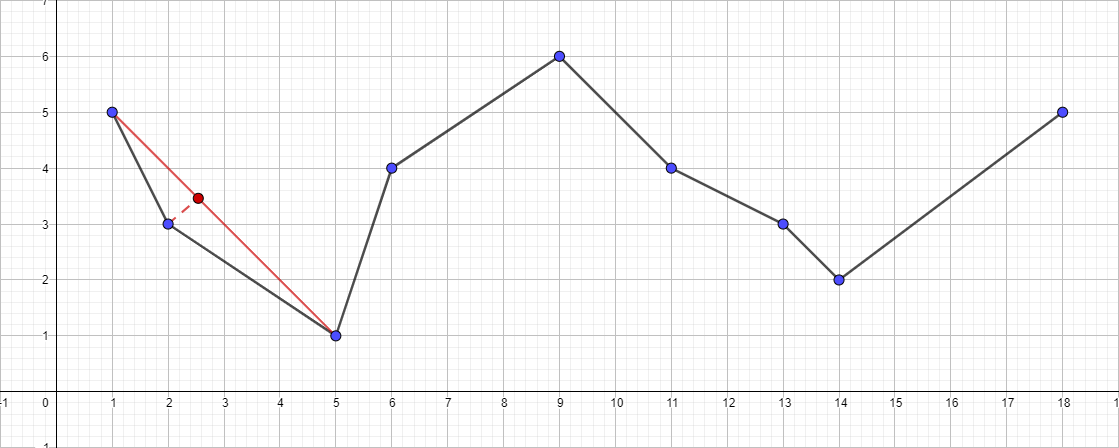
- Vérifiez sa distance au segment {1; 5} - {5; 1}. Dans ce cas, il est inférieur à 1, ce qui signifie que nous pouvons ignorer ce point en toute sécurité.
- Exécutez récursivement l'algorithme pour le segment {5; 1} - {18; 5} et trouvez le point le plus éloigné de ce segment ...
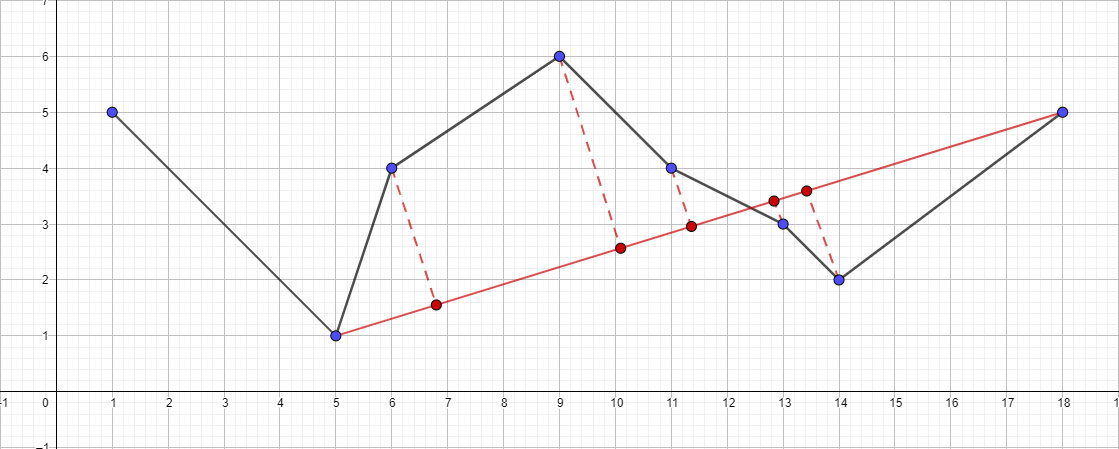
- Et ainsi de suite selon le même plan ...
Par conséquent, l'arborescence d'appels récursifs pour ces données de test ressemblera à ceci:
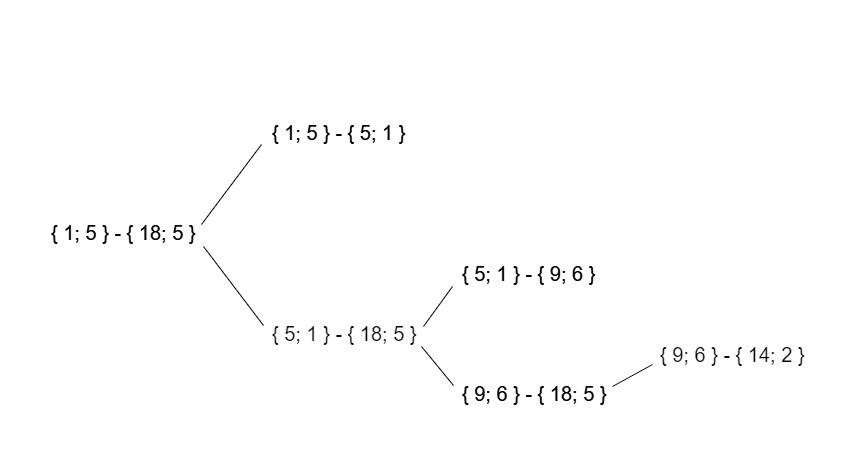
Temps de travail
La complexité attendue de l'algorithme est au mieux O (nlogn), c'est lorsque le numéro du point le plus éloigné est toujours lexicographiquement central. Cependant, dans le pire des cas, la complexité de l'algorithme est O (n ^ 2). Ceci est réalisé, par exemple, si le numéro du point le plus éloigné est toujours adjacent au numéro du point limite.
J'espère que mon article sera utile à quelqu'un, je voudrais également me concentrer sur le fait que si l'article suscite suffisamment d'intérêt parmi les lecteurs, je serai bientôt prêt à envisager des algorithmes pour simplifier la chaîne polygonale de Reumman-Witkam, Opheim et Lang. Merci de votre attention!