Lors de l'analyse de séries chronologiques stationnaires obtenues expérimentalement, en règle générale, lors de la préparation préliminaire (prétraitement) des données, il devient nécessaire de supprimer la tendance qui y existe.
Ici, une «nouvelle» méthode de mise en évidence des tendances sera proposée - simple, évidente et adaptée aux types de tendances très complexes.
Une tendance est généralement comprise comme une composante non harmonique à ultra-basse fréquence qui viole fortement la stationnarité du processus. La cause la plus courante d'une tendance dans les données obtenues expérimentalement est la «dérive zéro» de l'appareil de contrôle. L'intégration des données et certains autres types de traitement peuvent également provoquer une tendance. La présence d'une tendance déforme considérablement les résultats du traitement ultérieur des données (estimation spectrale, etc.), par conséquent, la suppression de la tendance est nécessaire. Dans certains cas, la tendance elle-même est une source précieuse d'informations (par exemple, lors de l'analyse des tendances à long terme des processus économiques ou météorologiques).
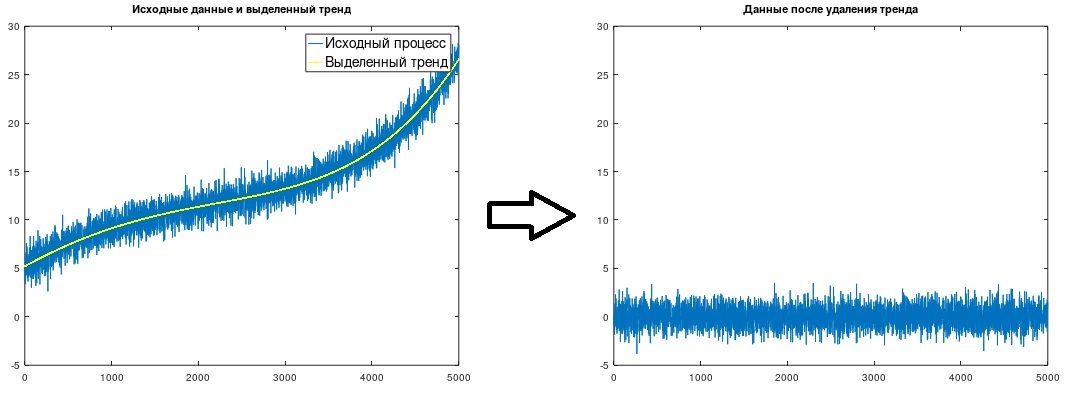Fig. 1. Isolement et suppression d'une tendanceEn règle générale, une tendance est modélisée à l'aide de fonctions linéaires ou de puissance (2e ou 3e ordre), dont les coefficients sont calculés en multipliant le processus par certaines séquences, puis en appliquant des formules assez complexes dérivées à l'aide de la méthode des moindres carrés. (voir, par exemple, J. Bendat, A. Pirsol, «Applied Analysis of Random Data», M., Mir, 1989.) Ce qui suit est une méthode légèrement modifiée, également basée sur la méthode des moindres carrés, qui est très facile à comprendre et à apprendre, et ne nécessite ni référence à des répertoires, ni calculs symboliques complexes indépendants pour obtenir les dépendances nécessaires, tout en vous permettant de modéliser la tendance avec des fonctions de toute nature. Cette méthode modifiée est si simple et évidente (une fois maîtrisée, les scripts peuvent ensuite être écrits de mémoire) qu'elle a probablement été "inventée" par plusieurs chercheurs plus d'une fois, mais je n'ai encore rien trouvé dans aucune des sources.
Pour mettre en évidence la tendance, une approximation du processus initial x [i], composé de N + 1 échantillons, est effectuée en utilisant un petit nombre de k composantes des fonctions de tendance u
j [i]:
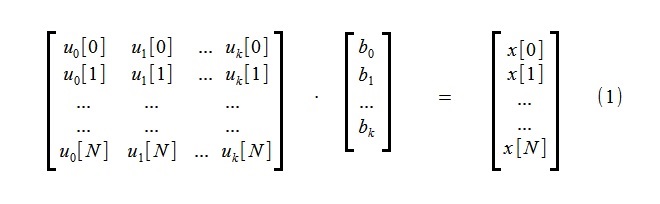
(Habituellement, les fonctions de puissance sont choisies comme fonctions u
j [i],
mais pour cette méthode c'est absolument sans principes)
Le système d'équations algébriques linéaires (1) comprend k équations inconnues b
j et N + 1.
Prendre la notation:
écrire plus compact
L'application de la méthode des moindres carrés à la recherche d'une solution approximative d'un système surdéterminé s'écrit sous forme matricielle comme suit:
Lors de l'écriture d'un script: Naturellement, il n'est pas nécessaire de stocker toute la grande matrice U, les éléments de la matrice U
T U et du vecteur U
T x peuvent être "accumulés" pas à pas.
Le système (4) d'équations k et k inconnues est résolu par des méthodes évidentes - eh bien, par exemple, nous l'écrivons comme ceci:
après quoi, en utilisant le b
j trouvé, nous pouvons construire la tendance θ [i] sous la forme
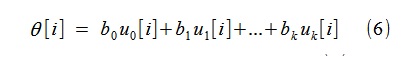
Par exemple, un processus aléatoire x [i] du formulaire a été simulé
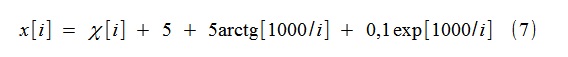
où χ [i] - bruit blanc gaussien avec une seule dispersion. La tendance est modélisée par des fonctions de type (2) (plus précisément, (8)), jusqu'au 4e ordre inclus (k = 4).
Lors de l'utilisation de fonctions de loi de puissance pour la modélisation des tendances, il convient de noter que la matrice U
T U (4) est théoriquement toujours réversible en raison de l'indépendance linéaire de ces fonctions, cependant, à des ordres élevés de k (ou de très longues réalisations de N, ce qui est moins critique), certains de ses éléments peuvent être très grand en valeur absolue. Aux ordres de k élevés, en cas de difficultés de calcul, il est recommandé d'utiliser des coefficients d'abaissement, par exemple, tels (8):
(Δt = 1), ce qui a été fait dans l'exemple considéré. La tendance représentée sur la figure 1 est obtenue.
Après avoir mis en évidence une tendance, elle doit naturellement être simplement soustraite des données source.
Remarque. Les sources faisant généralement autorité ne recommandent pas de travailler avec des modèles de tendance de l'ordre supérieur à k = 2 (parabole carrée). Que cela soit dû à la difficulté de déterminer les coefficients "d'amplitude" b
j par les méthodes traditionnelles, ou à l'épuisement des ordres de variables machine mentionnés ci-dessus, ou à la fausse affectation de composantes informatives du processus à la tendance, n'est pas très clair. Dans l'exemple donné, la tendance du 4e ordre est mise en évidence comme si elle était tout à fait plausible (bien qu'elle ne soit pas très différente de la tendance du 3e ordre). Pour les cas particulièrement difficiles, les sources recommandent d'utiliser une méthode différente - le filtrage passe-bas (non considéré ici).
En mettant en évidence une tendance, comme indiqué ci-dessus, la procédure n'est pas si compliquée, elle vous permet soit de sélectionner et d'analyser des tendances «lentes», soit, plus souvent, aide à obtenir des données de haute qualité - un processus aléatoire stationnaire centré approprié pour une analyse plus approfondie.