
Présentation
Cet article décrit les résultats d'une expérience menée dans le cadre du projet «Taux de change absolu». Le protocole expérimental peut être consulté en cliquant sur le lien .
Le projet « Taux de change absolu » est engagé dans l'analyse des taux de change appariés, la répartition des taux de change absolus à partir d'eux et leur analyse. Dans le cadre du projet, une méthodologie de conversion des taux de paire en taux de change absolus a été obtenue. Pour cela, l'ABS en devise absolue est défini. Toutes les devises disponibles sont exprimées en termes d'ABS.
Une description détaillée de la technologie est donnée dans l'article « Des paires de devises aux taux de change absolus ».
À ce jour, plusieurs articles ont déjà été publiés sur l'application de la méthode du taux de change absolu. J'apporte les deux derniers.
L'article « Étude de l'interdépendance des monnaies mondiales par la corrélation des taux absolus » décrit l'une des applications de la technologie des taux de change absolus. Une méthode formelle de calcul de la relation entre différentes devises est présentée.
L'article « La méthode du portefeuille de Markowitz appliquée au marché des changes » décrit une technologie jusqu'alors inaccessible pour optimiser le portefeuille de devises.
Ce qui suit décrit la méthode de conversion des taux de change (relatifs) de paire en absolus. Les paramètres numériques de la transformation et la méthodologie de leur calcul sont donnés.
Dans le fichier source, les taux de change quotidiens sont automatiquement chargés quotidiennement et les taux absolus sont calculés à partir d'eux.
La matrice de transformation a été obtenue en 2017. Il a été calculé aux taux de change de paire réels en minimisant l'erreur d'écart des taux de paire restaurés par rapport à l'absolu. Depuis lors, aucune analyse d'erreur n'a été effectuée sur les données modernes.
Les résultats de vérification inattendus décrits ci-dessous ont conduit au développement d'une nouvelle technique d'obtention de la matrice de transformation. De plus, une erreur a été détectée lors du traitement des devis importés.
Motifs théoriques
Pour obtenir des taux de change absolus, vous devez effectuer la conversion suivante. Pour commencer, les cours en binôme sont logarithmes. Ensuite, nous les multiplions par la matrice de transformation inverse. À la fin, nous revenons de l'échelle logarithmique en utilisant un exposant.
Pour la transition ultérieure vers des cours en binôme, les cours absolus doivent être enregistrés. Multipliez ensuite par la matrice de transformation directe. Nous concluons comme avant en utilisant l'exposant.
La technologie est décrite plus en détail dans l'article « Des paires de devises aux taux absolus des devises individuelles » (seul cet article de 2018 donne une représentation transposée des matrices de transformation contrairement à la présentation de cet article).
La matrice directe est facilement déterminée. Les lignes correspondent aux devises et les colonnes aux paires de devises. La matrice est très clairsemée et se compose de zéros, de uns et de moins.
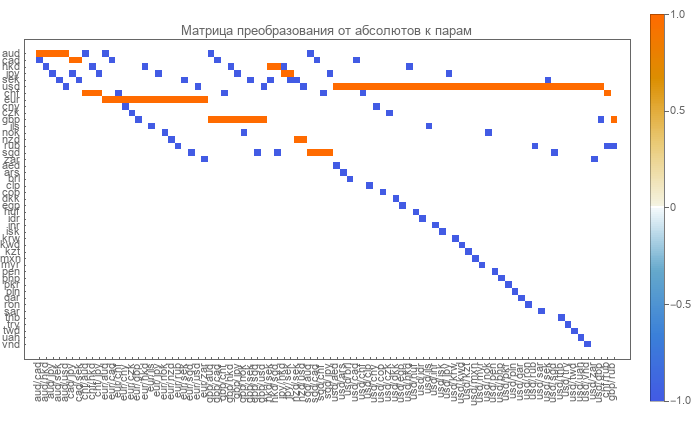
Les zéros indiquent l'absence d'une telle paire et d'une telle monnaie. L'unité correspond à la devise du numérateur de la paire. Le moins indique la devise dans le dénominateur de la paire.
La matrice de transformation inverse des paires en taux absolus n'est pas définie. Il faut le calculer. La méthode la plus évidente consiste à minimiser l'erreur de récupération de paire. Ce qui a été fait pour calculer cette matrice en 2017. Nous donnons une représentation graphique de cette matrice.
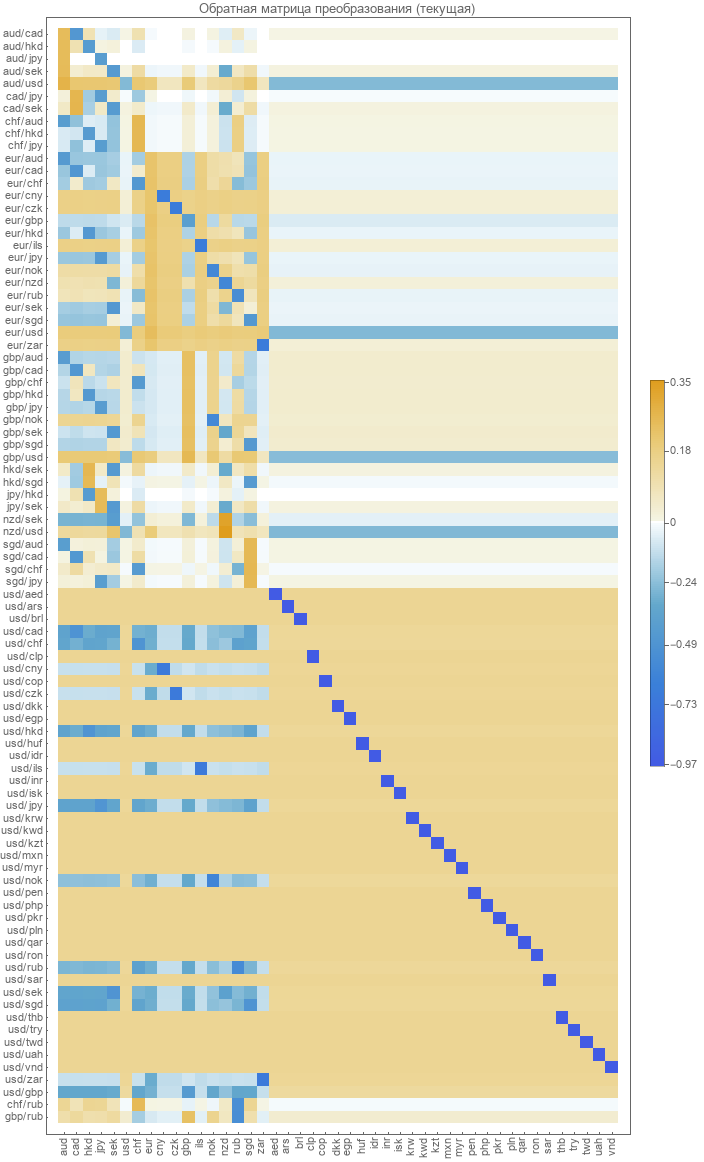
Vérification de la précision d'un modèle existant
Pour la matrice actuelle, des taux de change de paire absolus et rétablis ont été obtenus. Il y avait de fortes différences entre les parcours jumelés originaux et restaurés.

Ensuite, le calcul des erreurs de récupération pour toutes les paires a été effectué.
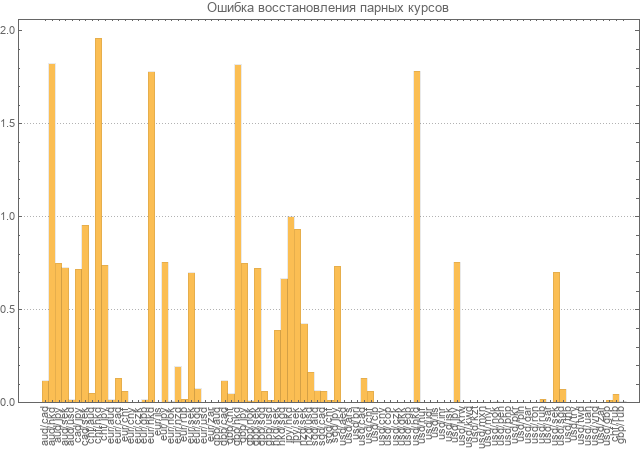
L'erreur a été considérée comme la moyenne des écarts relatifs pris modulo. Comme le montre le diagramme, les erreurs de nombreuses paires sont presque deux fois plus importantes que les valeurs elles-mêmes.
Bien entendu, ce niveau d'erreur ne permet pas de considérer le modèle comme cohérent et nécessite un recomptage.
Matrice pseudoinverse d'une ligne
La première chose que nous allons essayer est de simplement calculer la matrice inverse pour la matrice de transformation directe. Du fait que la matrice n'est pas carrée, nous devrons utiliser la transformation pseudoinverse . Le résultat est le suivant.
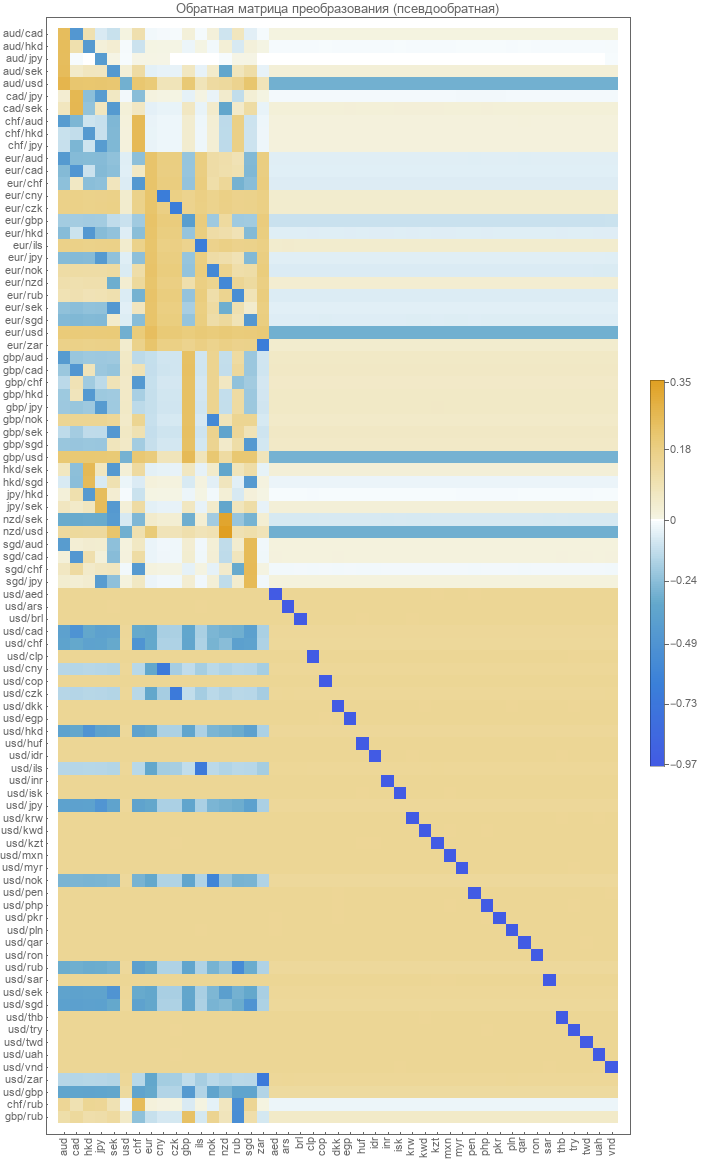
C'est très similaire à ce que nous avons obtenu plus tôt en utilisant des taux de change de paire réels pour l'optimisation.
Nous calculons les cours absolus. Ensuite, restaurez à partir des cours de paire absolus. Le tableau des erreurs est le suivant.

Les erreurs se sont également révélées importantes, comme dans l'évaluation ci-dessus. Ce modèle ne peut pas non plus nous convenir.
Calcul de la matrice inverse à travers des composants linéairement indépendants
Si nous analysons la matrice de transformation directe en détail, nous pouvons constater qu'elle a une forme dégénérée (le rang de la matrice est inférieur au nombre de lignes de devise). En d'autres termes, il y a des lignes linéairement dépendantes dans la matrice directe. Et donc, nous ne pouvons pas obtenir une matrice inverse acceptable.
Pour sortir de cette situation, la solution suivante a été proposée. Dans la transition des cours absolus aux cours jumelés, vous devez d'abord passer à des composants linéairement indépendants. Et ensuite seulement passer aux paires. Les matrices de transition des cours absolus aux composants et des composants aux cours appariés seront non dégénérées et des matrices inverses pourront être obtenues.
Pour rechercher des composants linéairement indépendants, il est nécessaire d'attacher une matrice d'unités de paires de cours à la matrice de transformation directe. Ainsi, nous obtenons deux matrices de la transition des cours absolus à la paire et la matrice attachée de la transition de la paire à la paire.

Nous allons maintenant effectuer des transformations standard vers la forme échelonnée de la partie supérieure de cette matrice combinée (en fait, les outils standard du package mathématique Wolfram Mathematica mènent plus loin vers la forme diagonale ). En conséquence, il a été possible d'obtenir la matrice transformée suivante.

Maintenant, dans les colonnes de cette matrice, nous avons des composants linéairement indépendants. De plus, nous pouvons passer à eux à la fois à partir de cours absolus (la partie supérieure de la matrice) et de cours appariés (la partie inférieure de la matrice transformée combinée).
Nous isolons ces matrices de transition en composants linéairement indépendants. Voici la matrice de transition pour les composants des cours absolus.
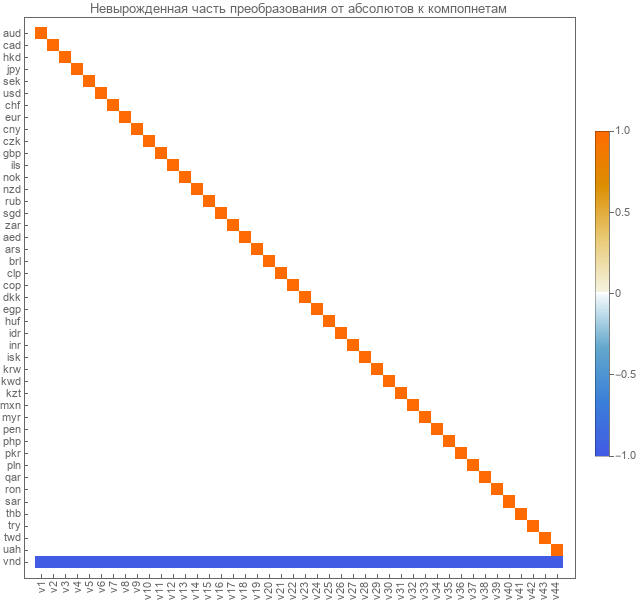
Voici la matrice de transition des cours par paires aux composants linéairement indépendants.

La transition des absolus aux composants s'effectue à travers la matrice calculée ci-dessus. La transformation inverse des composants en absolus se fait via la matrice inverse. Du fait qu'elle sera non dégénérée, une bonne matrice inverse peut être obtenue. Nous recevrons en pseudo-inverse. Voici son point de vue.

Vous pouvez maintenant obtenir la matrice de transformation inverse complète des paires aux absolus. Pour ce faire, nous multiplions la matrice de transformation des paires en composants par la matrice de transformation inverse des composants en absolus. Elle ressemble à ça.

Bien que nous ayons déjà vu un similaire ci-dessus, mais toujours la matrice est différente. Nous examinons les résultats qu'il donne. Nous calculerons les cours absolus, et à partir d'eux, nous restaurerons déjà les paires. L'erreur de récupération était la suivante.

Sur toutes les paires sauf deux, presque zéro erreur. Nous découvrons ce qui ne va pas avec ces paires.
Il s'avère que dans deux paires de devises, les mauvaises données sont acceptées. Pour jpy / hkd et jpy / sek, les données vont en lots de 10000 et 100 pièces. Il est nécessaire de corriger et revérifier.
Après avoir corrigé les cours de paire d'entrée (se débarrasser des lots) et recalculé les cours de paire absolus et restaurés, nous examinons l'erreur de récupération.

Vous avez une erreur à 0,3%. Un niveau d'erreur tout à fait acceptable.
Voici un exemple de tableau de cours absolu.
Voici un exemple des taux de change de paire d'origine et restaurés.

Puisque nous avons recalculé la nouvelle matrice de la transformation inverse, nous présentons à nouveau des données sur les derniers taux absolus de toutes les devises participantes.
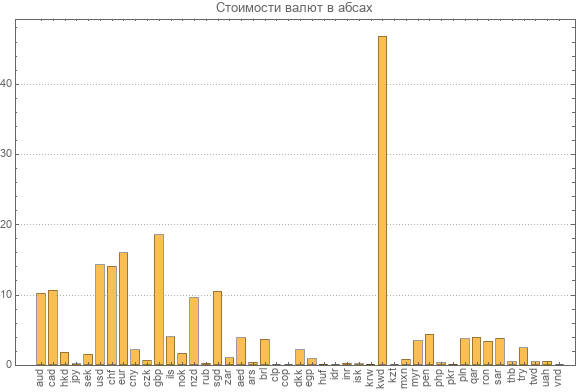
Vous pouvez voir la devise la plus chère. Il s'agit d'un dinar koweïtien d'une valeur de près de 47 abs. La plus petite valeur absolue du dong vietnamien est de 0,003 abs.
Conclusions
À la suite des études, il a été constaté que la méthode actuelle de calcul des taux absolus donne une erreur significative. De plus, une erreur a été détectée dans les données source.
Nous avons réussi à obtenir la matrice de transformation inverse de paires en absolus uniquement en utilisant la méthode de transformation en un plus petit nombre de composants linéairement indépendants avec une matrice de transformation non dégénérée.
La méthode d'obtention de la matrice de transformation inverse n'a pas utilisé de données de taux de paires. Et donc indépendant d'eux.
La vérification de la conversion sur des parcours réels a montré un faible niveau d'erreur. D'où il a été conclu que la matrice trouvée de la transformation inverse est applicable des taux de change appariés à l'absolu.
La méthode ne prétend pas être achevée et vérifiée mathématiquement, mais en tant que solution acceptable, elle sera utilisée pour d'autres études sur ses taux de change absolus.