Optlib Implémentation d'un algorithme d'optimisation génétique à Rust

Cet article décrit la bibliothèque optlib , conçue pour résoudre les problèmes d'optimisation globale dans le langage Rust. Au moment d'écrire ces lignes, cette bibliothèque implémente un algorithme génétique pour trouver le minimum global d'une fonction. La bibliothèque optlib n'est pas liée à un type d'entrée spécifique pour une fonction optimisée. De plus, la bibliothèque est construite de telle manière que lors de l'utilisation de l'algorithme génétique, il est facile de changer les algorithmes de croisement, de mutation, de sélection et d'autres étapes de l'algorithme génétique. En fait, l'algorithme génétique est assemblé comme s'il s'agissait de cubes.

Le problème de l'optimisation globale

Le problème d'optimisation est généralement formulé comme suit.

Pour une fonction donnée f ( x ), parmi toutes les valeurs possibles de x, trouver une valeur x 'telle que f (x') prenne une valeur minimale (ou maximale). De plus, x peut appartenir à différents ensembles - nombres naturels, nombres réels, nombres complexes, vecteurs ou matrices.

Par l'extrémum de la fonction f ( x ), nous entendons un point x ' auquel la dérivée de la fonction f ( x ) est égale à zéro.

Il existe de nombreux algorithmes garantissant de trouver l'extremum de la fonction, qui est un minimum ou un maximum local près d'un point de départ donné x ₀ . De tels algorithmes comprennent, par exemple, des algorithmes de descente de gradient. Cependant, dans la pratique, il est souvent nécessaire de trouver le minimum (ou maximum) global d'une fonction qui, dans une gamme donnée de x, en plus d'un extremum global, a de nombreux extrema locaux.

Les algorithmes de gradient ne peuvent pas faire face à l'optimisation d'une telle fonction, car leur solution converge vers l'extremum le plus proche près du point de départ. Pour les problèmes de recherche d'un maximum ou d'un minimum global, les algorithmes dits d'optimisation globale sont utilisés. Ces algorithmes ne garantissent pas de trouver un extremum global, car sont des algorithmes probabilistes, mais il ne reste plus qu'à essayer différents algorithmes pour une tâche spécifique et voir quel algorithme sera le mieux en mesure d'optimiser, de préférence dans les plus brefs délais et avec la probabilité maximale de trouver un extremum global.

L'un des algorithmes les plus connus (et difficiles à mettre en œuvre) est l'algorithme génétique.

Le schéma général de l'algorithme génétique

L'idée d'un algorithme génétique est née progressivement et s'est formée à la fin des années 1960 - début des années 1970. Les algorithmes génétiques ont connu un développement puissant après la sortie du livre de John Holland «Adaptation dans les systèmes naturels et artificiels» (1975)

L'algorithme génétique est basé sur la modélisation d'une population d'individus sur un grand nombre de générations. Dans le processus de l'algorithme génétique, de nouveaux individus avec les meilleurs paramètres apparaissent et les individus les moins performants meurent. Pour plus de précision, les termes suivants sont utilisés dans l'algorithme génétique.

• Un individu est une valeur de x parmi l'ensemble des valeurs possibles avec la valeur de la fonction objectif pour un point x donné.
• Chromosomes - la valeur de x .
• Chromosome - la valeur de x _i si x est un vecteur.
• La fonction fitness (fonction fitness, fonction objectif) est la fonction optimisée f ( x ).
• Une population est un ensemble d'individus.
• Génération - le nombre d'itérations de l'algorithme génétique.

Chaque individu représente une valeur de x parmi l'ensemble de toutes les solutions possibles. La valeur de la fonction optimisée (à l'avenir, par souci de concision, nous supposons que nous recherchons le minimum de la fonction) est calculée pour chaque valeur de x . Nous supposons que moins la fonction objectif est importante, meilleure est cette solution.

Les algorithmes génétiques sont utilisés dans de nombreux domaines. Par exemple, ils peuvent être utilisés pour sélectionner des poids dans les réseaux de neurones. De nombreux systèmes de CAO utilisent un algorithme génétique pour optimiser les paramètres de l'appareil afin de répondre aux exigences spécifiées. De plus, des algorithmes d'optimisation globale peuvent être utilisés pour sélectionner l'emplacement des conducteurs et des éléments sur la carte.

Le diagramme structurel de l'algorithme génétique est illustré dans la figure suivante:

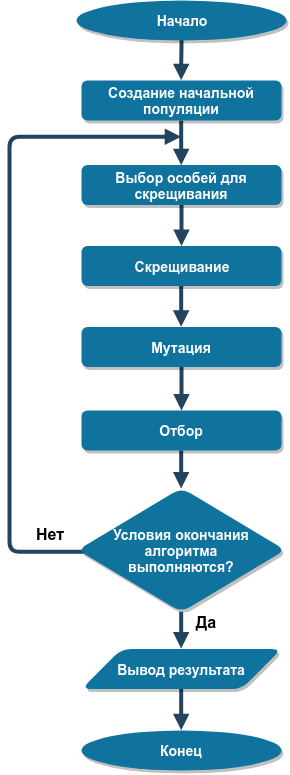
Nous considérons chaque étape de l'algorithme plus en détail.

Créer une population initiale

La première étape de l'algorithme est la création de la population initiale, c'est-à-dire la création de nombreux individus avec différentes valeurs de chromosomes x . En règle générale, la population initiale est créée à partir d'individus ayant une valeur chromosomique aléatoire, tout en essayant de garantir que les valeurs chromosomiques de la population couvrent la zone de recherche de la solution de manière relativement uniforme, à moins qu'il n'y ait des hypothèses quant à l'emplacement de l'extremum global.

Au lieu de distribuer aléatoirement des chromosomes, vous pouvez créer des chromosomes afin que les valeurs initiales de x soient uniformément réparties dans la zone de recherche avec une étape donnée, qui dépend du nombre d'individus qui seront créés à ce stade de l'algorithme.

Plus il y aura d'individus créés à ce stade, plus il est probable que l'algorithme trouvera la bonne solution, et à mesure que la taille de la population initiale augmente, en règle générale, moins d'itérations de l'algorithme génétique (nombre de générations) sont nécessaires. Cependant, avec l'augmentation de la taille de la population, un nombre croissant de calculs de la fonction objective et la performance d'autres opérations génétiques aux étapes suivantes de l'algorithme sont nécessaires. Autrement dit, avec une augmentation de la taille de la population, le temps de calcul d'une génération augmente.

En principe, la taille de la population ne doit pas rester constante tout au long du travail de l'algorithme génétique, souvent lorsque le nombre de génération augmente, la taille de la population peut être réduite, car au fil du temps, un nombre croissant d'individus seront plus proches de la solution souhaitée. Cependant, la taille de la population est souvent maintenue à peu près constante.

Sélection des individus pour le croisement

Après avoir créé une population, il est nécessaire de déterminer quels individus participeront à l'opération de croisement (voir le paragraphe suivant). Il existe différents algorithmes pour cette étape. Le plus simple d'entre eux est de croiser chaque individu avec chacun, mais à l'étape suivante, vous devrez effectuer trop d'opérations de croisement et calculer les valeurs de la fonction objectif.

Il est préférable de donner une plus grande chance d'accoupler des individus avec des chromosomes plus performants (avec une valeur minimale de la fonction objective), et les individus dont la fonction objective est plus (pire) de priver la capacité de laisser la progéniture.

Ainsi, à ce stade, vous devez créer des paires d'individus (ou pas nécessairement des paires si plus d'individus peuvent participer à la traversée), pour lesquels l'opération de traversée sera effectuée à l'étape suivante.

Ici, vous pouvez également appliquer différents algorithmes. Par exemple, créez des paires au hasard. Ou vous pouvez trier les individus par ordre croissant en fonction de la valeur de la fonction objectif et créer des paires d'individus situées plus près du début de la liste triée (par exemple, à partir d'individus dans la première moitié de la liste, dans le premier tiers de la liste, etc.) Cette méthode est mauvaise en ce qu'elle prend du temps pour trier les individus.

La méthode du tournoi est souvent utilisée. Lorsque plusieurs individus sont sélectionnés au hasard pour le rôle de chaque candidat au croisement, parmi lesquels l'individu ayant la meilleure valeur de la fonction objectif est envoyé au futur couple. Et même ici, on peut introduire un élément de hasard, donnant une petite chance à l'individu ayant la pire valeur de la fonction objectif de "vaincre" l'individu avec la meilleure valeur de la fonction objectif. Cela vous permet de maintenir une population plus hétérogène, la protégeant de la dégénérescence, c'est-à-dire d'une situation où tous les individus ont des valeurs chromosomiques approximativement égales, ce qui équivaut à bloquer l'algorithme à un extrême, peut-être pas global.

Le résultat de cette opération sera une liste de partenaires à traverser.

Croisement

Le croisement est une opération génétique qui crée de nouveaux individus avec de nouvelles valeurs chromosomiques. De nouveaux chromosomes sont créés sur la base des chromosomes des parents. Le plus souvent, lors du croisement d'un ensemble de partenaires, une fille est créée, mais théoriquement, plus d'enfants peuvent être créés.

L'algorithme de croisement peut également être implémenté de différentes manières. Si le type de chromosome est un nombre chez les individus, alors la chose la plus simple qui puisse être faite est de créer un nouveau chromosome comme moyenne arithmétique ou moyenne géométrique des chromosomes des parents. Pour de nombreuses tâches, cela suffit, mais le plus souvent, d'autres algorithmes basés sur des opérations binaires sont utilisés.

Les croisements au niveau du bit fonctionnent de telle manière que le chromosome fille se compose d'une partie des bits d'un parent et d'une partie des bits d'un autre parent, comme le montre la figure suivante:

Le point de partage parent est généralement sélectionné au hasard. Il n'est pas nécessaire de créer deux enfants avec une telle croix, souvent limitée à l'un d'eux.

Si le point de partage des chromosomes parents est un, un tel croisement est appelé point unique. Mais vous pouvez également utiliser le fractionnement multipoint, lorsque les chromosomes parents sont divisés en plusieurs sections, comme le montre la figure suivante:

Dans ce cas, plusieurs combinaisons de chromosomes filles sont possibles.

Si les chromosomes sont des nombres à virgule flottante, alors toutes les méthodes décrites ci-dessus peuvent leur être appliquées, mais elles ne seront pas très efficaces. Par exemple, si les nombres à virgule flottante sont croisés au niveau du bit, comme décrit précédemment, de nombreuses opérations de croisement créeront des chromosomes filles qui ne différeront de l'un des parents qu'à la décimale éloignée. La situation est particulièrement aggravée lors de l'utilisation de nombres à virgule flottante double précision.

Pour résoudre ce problème, il est nécessaire de rappeler que les nombres à virgule flottante selon la norme IEEE 754 sont stockés sous forme de trois nombres entiers: S (un bit), M et N, à partir desquels le nombre à virgule flottante est calculé comme x = (-1) ^S × M × 2 ^N. Une façon de croiser des nombres à virgule flottante consiste à diviser d'abord le nombre en composantes S, M, N, qui sont des nombres entiers, puis à appliquer les opérations de croisement au niveau du bit décrites ci-dessus aux nombres M et N, sélectionner le signe S de l'un des les parents, et à partir des valeurs obtenues pour faire un chromosome fille.

Dans de nombreux problèmes, un individu n'a pas un, mais plusieurs chromosomes, et il peut même être de différents types (nombres entiers et nombres à virgule flottante). Ensuite, il existe encore plus d'options pour traverser de tels chromosomes. Par exemple, lors de la création d'un individu fille, vous pouvez traverser tous les chromosomes des parents, ou vous pouvez transférer complètement certains chromosomes de l'un des parents sans changements.

Mutation

La mutation est une étape importante de l'algorithme génétique qui prend en charge la diversité des chromosomes des individus et réduit ainsi les chances que la solution converge rapidement vers un minimum local au lieu d'un minimum global. Une mutation est un changement aléatoire du chromosome d'un individu qui vient d'être créé par croisement.

En règle générale, la probabilité d'une mutation n'est pas réglée très haut afin que la mutation n'interfère pas avec la convergence de l'algorithme, sinon elle gâtera les individus avec des chromosomes réussis.

En plus du croisement, différents algorithmes peuvent être utilisés pour la mutation. Par exemple, vous pouvez remplacer un chromosome ou plusieurs chromosomes par une valeur aléatoire. Mais la mutation au niveau du bit est le plus souvent utilisée lorsqu'un ou plusieurs bits sont inversés dans le chromosome (ou dans plusieurs chromosomes), comme le montrent les figures suivantes.

Mutation d'un bit:

Mutation de plusieurs bits:

Le nombre de bits d'une mutation peut être prédéfini ou être une variable aléatoire.

À la suite de mutations, les individus peuvent se révéler à la fois plus réussis et moins réussis, mais cette opération permet un chromosome réussi avec des ensembles de zéros et ceux que les individus parentaux n'ont pas dû apparaître avec une probabilité non nulle.

Sélection

À la suite du croisement et de la mutation subséquente, de nouveaux individus apparaissent. S'il n'y avait pas d'étape de sélection, le nombre d'individus augmenterait de façon exponentielle, ce qui nécessiterait de plus en plus de RAM et de temps de traitement pour chaque nouvelle génération de la population. Par conséquent, après l'apparition de nouveaux individus, il est nécessaire d'éliminer la population des individus les moins performants. C'est ce qui se passe au stade de la sélection.

Les algorithmes de sélection peuvent également être différents. Souvent, les individus dont les chromosomes ne tombent pas dans un intervalle donné d'une recherche de solution sont d'abord rejetés.

Vous pouvez ensuite supprimer autant d'individus les moins performants que possible afin de maintenir une taille de population constante. Divers critères probabilistes de sélection peuvent également être appliqués, par exemple, la probabilité de sélection d'un individu peut dépendre de la valeur de la fonction objectif.

Conditions de fin d'algorithme

Comme dans les autres étapes de l'algorithme génétique, il existe plusieurs critères pour mettre fin à l'algorithme.

Le critère le plus simple pour terminer un algorithme est d'interrompre l'algorithme après un nombre d'itérations (génération) donné. Mais ce critère doit être utilisé avec précaution, car l'algorithme génétique est probabiliste, et différents démarrages de l'algorithme peuvent converger à différentes vitesses. Habituellement, le critère de terminaison par le numéro d'itération est utilisé comme critère supplémentaire au cas où l'algorithme ne trouverait pas de solution pendant un grand nombre d'itérations. Par conséquent, un nombre suffisamment grand doit être défini comme seuil du nombre d'itérations.

Un autre critère d'arrêt est que l'algorithme est interrompu si aucune nouvelle meilleure solution n'apparaît pour un nombre donné d'itérations. Cela signifie que l'algorithme a trouvé un extremum global ou est coincé dans un extremum local.

Il existe également une situation défavorable lorsque les chromosomes de tous les individus ont la même signification. Il s'agit de la soi-disant population dégénérée. Très probablement dans ce cas, l'algorithme est coincé dans un extrême, et pas nécessairement global. Seule une mutation réussie est capable de sortir une population de cet état, mais comme la probabilité d'une mutation est généralement établie par une petite mutation, et qu'il est loin du fait que la mutation créera un individu plus réussi, la situation avec une population dégénérée est généralement considérée comme une raison d'arrêter l'algorithme génétique. Pour vérifier ce critère, il est nécessaire de comparer les chromosomes de tous les individus, s'il existe des différences entre eux, et s'il n'y a pas de différences, puis arrêter l'algorithme.

Dans certains problèmes, il n'est pas nécessaire de trouver un minimum global, mais plutôt de trouver une bonne solution - une solution pour laquelle la valeur de la fonction objectif est inférieure à une valeur donnée. Dans ce cas, l'algorithme peut être arrêté à l'avance si la solution trouvée à la prochaine itération satisfait ce critère.

optlib

Optlib est une bibliothèque pour le langage Rust, conçue pour optimiser les fonctions. Au moment d'écrire ces lignes, seul l'algorithme génétique est implémenté dans la bibliothèque, mais à l'avenir, il est prévu d'étendre cette bibliothèque en y ajoutant de nouveaux algorithmes d'optimisation. Optlib est entièrement écrit en rouille.

Optlib est une bibliothèque open source distribuée sous licence MIT.

• Page sur github - https://github.com/Jenyay/rust-optimization
• Page sur crates.io - https://crates.io/crates/optlib
• Documentation - https://docs.rs/optlib

optlib :: génétique

De la description de l'algorithme génétique, on peut voir que de nombreuses étapes de l'algorithme peuvent être implémentées de différentes manières, en les sélectionnant de sorte que pour une fonction objective donnée, l'algorithme converge vers la bonne solution en un minimum de temps.

Le module optlib :: génétique est conçu de manière à pouvoir assembler l'algorithme génétique «à partir de cubes». Lors de la création d'une instance de la structure au sein de laquelle le travail de l'algorithme génétique aura lieu, vous devez spécifier les algorithmes qui seront utilisés pour créer la population, sélectionner les partenaires, les croisements, les mutations, la sélection et le critère utilisé pour interrompre l'algorithme.

La bibliothèque possède déjà les algorithmes les plus fréquemment utilisés pour les étapes de l'algorithme génétique, mais vous pouvez créer vos propres types qui implémentent les algorithmes correspondants.

Dans la bibliothèque, le cas où les chromosomes sont un vecteur de nombres fractionnaires, c'est-à-dire lorsque la fonction f ( x ) est minimisée, où x est le vecteur des nombres à virgule flottante ( f32 ou f64 ).

Exemple d'optimisation utilisant optlib :: génétique

Avant de commencer à décrire le module génétique en détail, considérons un exemple de son utilisation pour minimiser la fonction de Schwefel. Cette fonction multidimensionnelle est calculée comme suit:

$$

$$F (\ boldsymbol x) = 418.9829N - \ sum_ {i = 1} ^ {N} x_i \ sin (\ sqrt {| x_i |})$$

La fonction de Schweffel minimale dans l'intervalle -500 <= x _i <= 500 est située au point x ' , où tous les x _i = 420,9687 pour i = 1, 2, ..., N, et la valeur de la fonction à ce point est f ( x' ) = 0.

Si N = 2, alors l'image tridimensionnelle de cette fonction est la suivante:

Les extrêmes sont plus clairement visibles si nous construisons les lignes de niveau de cette fonction:

L'exemple suivant montre comment utiliser le module génétique pour trouver la fonction de Schweffel minimale. Vous pouvez trouver cet exemple dans le code source dans le dossier examples / génétique-schwefel.

//!    . //! //! y = f(x),  x = (x0, x1, ..., xi,... xn). //!      x' = (420.9687, 420.9687, ...) //!      xi - [-500.0; 500.0]. //! f(x') = 0 //! //! #  //! * ` ` -   . y = f(x). //! * `` -    , x = (x0, x1, x2, ..., xn). //! * `` -   x    . //! * `` -  . //! * `` -    . use optlib::genetic; use optlib::genetic::creation; use optlib::genetic::cross; use optlib::genetic::goal; use optlib::genetic::logging; use optlib::genetic::mutation; use optlib::genetic::pairing; use optlib::genetic::pre_birth; use optlib::genetic::selection; use optlib::genetic::stopchecker; use optlib::testfunctions; use optlib::Optimizer; ///    type Gene = f32; ///   type Chromosomes = Vec<Gene>; fn main() { //   //  .  xi     [-500.0; 500.0] let minval: Gene = -500.0; let maxval: Gene = 500.0; //      let population_size = 500; //   xi  . //  15-   let chromo_count = 15; let intervals = vec![(minval, maxval); chromo_count]; //      ( ) //      optlib::testfunctions let goal = goal::GoalFromFunction::new(testfunctions::schwefel); //       . // RandomCreator       . let creator = creation::vec_float::RandomCreator::new(population_size, intervals.clone()); //        //     . let partners_count = 2; let families_count = population_size / 2; let rounds_count = 5; let pairing = pairing::Tournament::new(partners_count, families_count, rounds_count); //   //      , //   -     let single_cross = cross::FloatCrossExp::new(); let cross = cross::VecCrossAllGenes::new(Box::new(single_cross)); //    //    (     ). let mutation_probability = 15.0; let mutation_gene_count = 3; let single_mutation = mutation::BitwiseMutation::new(mutation_gene_count); let mutation = mutation::VecMutation::new(mutation_probability, Box::new(single_mutation)); // .       , //     . let pre_births: Vec<Box<genetic::PreBirth<Chromosomes>>> = vec![Box::new( pre_birth::vec_float::CheckChromoInterval::new(intervals.clone()), )]; //    //   ,       1e-4 //   3000  (). let stop_checker = stopchecker::CompositeAny::new(vec![ Box::new(stopchecker::Threshold::new(1e-4)), Box::new(stopchecker::MaxIterations::new(3000)), ]); //    .  -   . //        NaN  Inf. //    ,     . let selections: Vec<Box<dyn genetic::Selection<Chromosomes>>> = vec![ Box::new(selection::KillFitnessNaN::new()), Box::new(selection::LimitPopulation::new(population_size)), ]; //     . //       , //       . let loggers: Vec<Box<genetic::Logger<Chromosomes>>> = vec![ Box::new(logging::StdoutResultOnlyLogger::new(15)), Box::new(logging::TimeStdoutLogger::new()), ]; //     let mut optimizer = genetic::GeneticOptimizer::new( Box::new(goal), Box::new(stop_checker), Box::new(creator), Box::new(pairing), Box::new(cross), Box::new(mutation), selections, pre_births, loggers, ); //    optimizer.find_min(); } 

Cet exemple peut être exécuté à partir de la racine source en exécutant la commande

 cargo run --bin genetic-schwefel --release 

Le résultat devrait ressembler à ceci:

 Solution: 420.962615966796875 420.940093994140625 420.995391845703125 420.968505859375000 420.950866699218750 421.003784179687500 421.001281738281250 421.300537109375000 421.001708984375000 421.012603759765625 420.880493164062500 420.925079345703125 420.967559814453125 420.999237060546875 421.011505126953125 Goal: 0.015625000000000 Iterations count: 3000 Time elapsed: 2617 ms 

La majeure partie de l'exemple de code est impliquée dans la création d'objets de trait pour les différentes étapes de l'algorithme génétique. Comme cela a été écrit au début de l'article, chaque étape de l'algorithme génétique peut être implémentée de différentes manières. Pour utiliser le module optlib :: génétique, vous devez créer des objets trait qui implémentent chaque étape d'une manière ou d'une autre. Tous ces objets sont ensuite transférés au constructeur de la structure GeneticOptimizer, au sein de laquelle l'algorithme génétique est implémenté.

La méthode find_min () de la structure GeneticOptimizer démarre l'exécution de l'algorithme génétique.

Types et objets de base

Caractéristiques de base du module optlib

La bibliothèque optlib a été développée dans le but que de nouveaux algorithmes d'optimisation soient ajoutés à l'avenir afin que le programme puisse facilement passer d'un algorithme d'optimisation à un autre.Par conséquent, le module optlib contient le trait Optimizer , qui comprend une seule méthode - find_min (), qui exécute l'algorithme d'optimisation lors de l'exécution. Ici, le type T est le type de l'objet, qui est un point dans l'espace de recherche de solution. Par exemple, dans l'exemple ci-dessus, il s'agit de Vec <Gene> (où Gene est un alias pour f32). C'est-à-dire que c'est le type dont l'objet est alimenté à l'entrée de la fonction objectif.

Le trait Optimizer est déclaré dans le module optlib comme suit:

 pub trait Optimizer<T> { fn find_min(&mut self) -> Option<(&T, f64)>; } 

La méthode find_min () de l'optim_ trait doit renvoyer un objet de type Option <(& T, f64)>, où & T dans le tuple renvoyé est la solution trouvée, et f64 est la valeur de la fonction objectif pour la solution trouvée. Si l'algorithme n'a pas pu trouver de solution, la fonction find_min () doit retourner None.

Étant donné que de nombreux algorithmes d'optimisation stochastique utilisent des agents dits (en termes d'algorithme génétique, un agent est un individu), le module optlib contient également le trait AlgorithmWithAgents avec une seule méthode get_agents () qui devrait renvoyer le vecteur d'agent.

Un agent, à son tour, est une structure qui implémente un autre trait de optlib - Agent .

Les traits AlgorithmWithAgents et Agent sont déclarés dans le module optlib comme suit:

 pub trait AlgorithmWithAgents<T> { type Agent: Agent<T>; fn get_agents(&self) -> Vec<&Self::Agent>; } pub trait Agent<T> { fn get_parameter(&self) -> &T; fn get_goal(&self) -> f64; } 

Pour AlgorithmWithAgents et Agent, le type T a la même signification que pour l'Optimizer, c'est-à-dire qu'il s'agit du type d'objet pour lequel la valeur de la fonction objectif est calculée.

Structure GeneticOptimizer - Implémentation d'un algorithme génétique

Les deux types sont implémentés pour la structure GeneticOptimizer - Optimizer et AlgorithmWithAgents.

Chaque étape de l'algorithme génétique est représentée par son propre type, qui peut être implémenté à partir de zéro ou utiliser l'une des implémentations optlib :: génétique disponibles à l'intérieur. Pour chaque étape de l'algorithme génétique, à l'intérieur du module optlib :: génétique se trouve un sous-module avec des structures et fonctions auxiliaires qui mettent en œuvre les algorithmes les plus fréquemment utilisés des étapes de l'algorithme génétique. À propos de ces modules seront discutés ci-dessous. À l'intérieur de certains de ces sous-modules se trouve également un sous-module vec_float qui implémente les étapes de l'algorithme dans le cas où la fonction objectif est calculée à partir d'un vecteur de nombres à virgule flottante (f32 ou f64).

Le constructeur de la structure GeneticOptimizer est déclaré comme suit:

 impl<T: Clone> GeneticOptimizer<T> { pub fn new( goal: Box<dyn Goal<T>>, stop_checker: Box<dyn StopChecker<T>>, creator: Box<dyn Creator<T>>, pairing: Box<dyn Pairing<T>>, cross: Box<dyn Cross<T>>, mutation: Box<dyn Mutation<T>>, selections: Vec<Box<dyn Selection<T>>>, pre_births: Vec<Box<dyn PreBirth<T>>>, loggers: Vec<Box<dyn Logger<T>>>, ) -> GeneticOptimizer<T> { ... } ... } 

Le constructeur de GeneticOptimizer accepte de nombreux types d'objets qui affectent chaque étape de l'algorithme génétique, ainsi que la sortie des résultats:

• objectif: Box <dyn Goal <T>> - fonction objectif;
• stop_checker: Case <dyn StopChecker <T>> - critère d'arrêt;
• creator: Box <dyn Creator <T>> - crée la population initiale;
• appariement: Box <dyn Pairing <T>> - algorithme de sélection des partenaires pour le croisement;
• cross: Box <dyn Cross <T>> - algorithme de croisement;
• mutation: Box <dyn Mutation <T>> - algorithme de mutation;
• sélections: Vec <Box <dyn Selection <T> >> - un vecteur d'algorithmes de sélection;
• pre_births: Vec <Box <dyn PreBirth <T> >> - un vecteur d'algorithmes pour détruire les chromosomes infructueux avant de créer des individus;
• enregistreurs: Vec <Box <dyn Logger <T> >> - un vecteur d'objets qui préservent le journal de l'algorithme génétique.

Pour exécuter l'algorithme, vous devez exécuter la méthode find_min () du trait Optimizer. De plus, la structure GeneticOptimizer possède la méthode next_iterations (), qui peut être utilisée pour continuer le calcul une fois la méthode find_min () terminée.

Parfois, après l'arrêt d'un algorithme, il est utile de modifier les paramètres de l'algorithme ou les méthodes utilisées. Cela peut être fait en utilisant les méthodes suivantes de la structure GeneticOptimizer: replace_pairing (), replace_cross (), replace_mutation (), replace_pre_birth (), replace_selection (), replace_stop_checker (). Ces méthodes vous permettent de remplacer les objets trait transmis à la structure GeneticOptimizer lors de sa création.

Les principaux types d'algorithme génétique sont discutés dans les sections suivantes.

Caractéristique de but - fonction objective

Le trait Goal est déclaré dans le module optlib :: génétique comme suit:

 pub trait Goal<T> { fn get(&self, chromosomes: &T) -> f64; } 

La méthode get () doit renvoyer la valeur de la fonction objectif pour le chromosome donné.

À l'intérieur du module optlib :: génétique :: objectif , il y a une structure GoalFromFunction qui implémente le trait Goal. Pour cette structure, il existe un constructeur qui prend une fonction, qui est la fonction cible. Autrement dit, en utilisant cette structure, vous pouvez créer un objet de type Objectif à partir d'une fonction régulière.

Caractère créateur - création d'une population initiale

Le trait Créateur décrit le «créateur» de la population initiale. Ce trait est déclaré comme suit:

 pub trait Creator<T: Clone> { fn create(&mut self) -> Vec<T>; } 

La méthode create () doit renvoyer le vecteur des chromosomes sur la base duquel la population initiale sera créée.

Dans le cas où une fonction de plusieurs nombres à virgule flottante est optimisée, le module optlib :: génétique :: créateur :: vec_float a une structure RandomCreator <G> pour créer une distribution initiale de chromosomes de manière aléatoire.

Ci-après, le type <G> est le type d'un chromosome dans le vecteur chromosomique (parfois le terme "gène" est utilisé à la place du terme "chromosome"). Fondamentalement, le type <G> signifiera le type f32 ou f64 si les chromosomes sont du type Vec <f32> ou Vec <f64>.

La structure de RandomCreator <G> est déclarée comme suit:

 pub struct RandomCreator<G: Clone + NumCast + PartialOrd> { ... } 

Ici, NumCast est un type de la caisse numérique. Ce type vous permet de créer un type à partir d'autres types numériques à l'aide de la méthode from ().

Pour créer une structure RandomCreator <G>, vous devez utiliser la fonction new (), qui est déclarée comme suit:

 pub fn new(population_size: usize, intervals: Vec<(G, G)>) -> RandomCreator<G> { ... } 

Ici, population_size est la taille de la population (le nombre d'ensembles de chromosomes à créer), et les intervalles est le vecteur de tuples de deux éléments - la valeur minimale et maximale du chromosome (gène) correspondant dans l'ensemble de chromosomes, et la taille de ce vecteur détermine combien de chromosomes sont contenus dans l'ensemble de chromosomes chaque individu.

Dans l'exemple ci-dessus, la fonction Schweffel a été optimisée pour 15 variables de type f32. Chaque variable doit se situer dans la plage [-500; 500]. Autrement dit, pour créer une population, le vecteur d'intervalle doit contenir 15 tuples (-500.0f32, 500.0f32).

Appariement de types - sélection des partenaires à traverser

Le trait d'appariement est utilisé pour sélectionner les individus qui se métisseront. Ce trait est déclaré comme suit:

 pub trait Pairing<T: Clone> { fn get_pairs(&mut self, population: &Population<T>) -> Vec<Vec<usize>>; } 

La méthode get_pairs () prend un pointeur sur la structure de la population , qui contient tous les individus de la population, et également à travers cette structure, vous pouvez trouver les meilleurs et les pires individus de la population.

La méthode d'appariement get_pairs () doit renvoyer un vecteur qui contient des vecteurs qui stockent les indices des individus qui se métisseront. Selon l'algorithme de croisement (qui sera discuté dans la section suivante), deux individus ou plus peuvent se croiser.

Par exemple, si des individus avec l'index 0 et 10, 5 et 2, 6 et 3 sont croisés, la méthode get_pairs () doit renvoyer le vecteur vec! [Vec! [0, 10], vec! [5, 2], vec! [ 6, 3]].

Le module optlib :: génétique :: appariement contient deux structures qui implémentent divers algorithmes de sélection de partenaires.

Pour la structure RandomPairing , le type Pairing est implémenté de manière à ce que les partenaires soient sélectionnés au hasard pour le croisement.

Pour la structure Tournament , le trait Pairing est implémenté de telle manière que la méthode du tournoi est utilisée. La méthode du tournoi implique que chaque individu qui participera au cross doit vaincre un autre individu (la valeur de la fonction objective de l'individu gagnant doit être moindre). Si la méthode du tournoi utilise un tour, cela signifie que deux individus sont sélectionnés au hasard, et qu'un individu avec une valeur plus faible de la fonction objective parmi ces deux individus entre dans la future «famille». Si plusieurs tours sont utilisés, l'individu gagnant de cette manière devrait gagner contre plusieurs individus aléatoires.

Le constructeur de la structure du tournoi est déclaré comme suit:

 pub fn new(partners_count: usize, families_count: usize, rounds_count: usize) -> Tournament { ... } 

Ici:

• partners_count - le nombre d'individus requis pour la traversée;
• families_count - le nombre de "familles", c'est-à-dire ensembles d'individus qui produiront une progéniture;
• rounds_count - le nombre de tours dans le tournoi.

Comme autre modification de la méthode du tournoi, vous pouvez utiliser le générateur de nombres aléatoires pour donner une petite chance de vaincre les individus avec la pire valeur de la fonction objectif, c'est-à-dire pour que la probabilité de victoire soit influencée par la valeur de la fonction objectif, et plus la différence entre les deux concurrents est grande, plus les chances de gagner le meilleur individu sont grandes, et avec des valeurs presque égales de la fonction objectif, la probabilité de victoire d'un individu serait proche de 50%.

Type Cross - Crossing

Après la formation de «familles» d'individus, pour le croisement, vous devez traverser leurs chromosomes pour obtenir des enfants avec de nouveaux chromosomes. L'étape de croisement est représentée par le type Cross , qui est déclaré comme suit:

 pub trait Cross<T: Clone> { fn cross(&mut self, parents: &[&T]) -> Vec<T>; } 

La méthode cross () croise un ensemble de parents. Cette méthode accepte le paramètre parents - une tranche de références aux chromosomes des parents (pas les individus eux-mêmes) - et devrait renvoyer un vecteur des nouveaux chromosomes. La taille des parents dépend de l'algorithme de sélection des partenaires à croiser à l'aide du trait Pairing , décrit dans la section précédente. Souvent utilisé un algorithme qui crée de nouveaux chromosomes basés sur les chromosomes de deux parents, alors la taille des parents sera égale à deux.

Le module optlib :: génétique :: cross contient des structures pour lesquelles le type Cross est implémenté avec différents algorithmes de croisement.

• VecCrossAllGenes - une structure conçue pour traverser les chromosomes, lorsque chaque individu a un ensemble de chromosomes - c'est un vecteur. Le constructeur VecCrossAllGenes accepte un type d'objet Cross qui sera appliqué à tous les éléments des vecteurs chromosomiques parents. Dans ce cas, la taille des vecteurs chromosomiques parents doit être de la même taille. L'exemple ci-dessus utilise la structure VecCrossAllGenes car le chromosome des individus utilisés est de type Vec <f32>.
• CrossMean est une structure qui croise deux nombres de telle manière qu'en tant que chromosome fille, il y aura un nombre calculé comme la moyenne arithmétique des chromosomes parents.
• FloatCrossGeometricMean est une structure qui croise deux nombres de telle manière qu'en tant que chromosome fille, il y aura un nombre calculé comme la moyenne géométrique des chromosomes parents. Il devrait y avoir des nombres à virgule flottante sous forme de chromosomes.
• CrossBitwise - croisement au point unique au niveau du bit de deux nombres.
• FloatCrossExp - croisement ponctuel au niveau du bit de nombres à virgule flottante. La mantisse indépendante et les exposants parentaux se croisent. L'enfant reçoit le signe de l'un des parents.

Le module optlib :: génétique :: cross contient également des fonctions pour les nombres croisés au niveau du bit de différents types - entier et virgule flottante.

Type Mutation - Mutation

Après le croisement, il est nécessaire de muter les enfants obtenus afin de maintenir la diversité des chromosomes, et la population n'est pas passée à un état dégénéré. Pour la population, le trait Mutation est prévu, qui est déclaré comme suit:

 pub trait Mutation<T: Clone> { fn mutation(&mut self, chromosomes: &T) -> T; } 

La seule méthode de mutation () du trait Mutation prend une référence à un chromosome et devrait renvoyer un chromosome éventuellement altéré. En règle générale, une faible probabilité de mutation est établie, par exemple, quelques pour cent, de sorte que les chromosomes obtenus sur la base des parents restent, et améliorent ainsi la population.

Certains algorithmes de mutation sont déjà implémentés dans le module optlib :: génétique :: mutation .

Ce module, par exemple, contient la structure VecMutation , qui fonctionne de manière similaire à la structure VecCrossAllGenes , c'est-à-dire si le chromosome est un vecteur, VecMutation accepte le type d'objet Mutation et l'applique avec une probabilité donnée pour tous les éléments du vecteur, créant un nouveau vecteur avec des gènes mutés (éléments du vecteur chromosome).

Le module optlib :: génétique :: mutation contient également une structure BitwiseMutation pour laquelle le trait Mutation est implémenté. Cette structure inverse un nombre donné de bits aléatoires dans le chromosome qui lui est transmis. Il est conseillé d'utiliser cette structure avec la structure VecMutation.

Trait pré-naissance - présélection

Après le croisement et la mutation, la phase de sélection se produit généralement, au cours de laquelle les individus les plus infructueux sont détruits. Cependant, dans la mise en œuvre de l'algorithme génétique dans la bibliothèque génétique optlib ::, avant l'étape de sélection, il existe une autre étape à laquelle les chromosomes infructueux peuvent être éliminés. Cette étape a été ajoutée car le calcul de la fonction objectif pour les individus prend souvent beaucoup de temps, et il n'est pas nécessaire de le calculer si les chromosomes ne tombent pas dans l'intervalle de recherche connu. Par exemple, dans l'exemple ci-dessus, les chromosomes qui ne tombent pas sur le segment [-500; 500].

Pour effectuer un tel préfiltrage, le trait PreBirth est prévu , qui est déclaré comme suit:

 pub trait PreBirth<T: Clone> { fn pre_birth(&mut self, population: &Population<T>, new_chromosomes: &mut Vec<T>); } 

La seule méthode preBirth () du trait PreBirth est une référence à la structure de la population mentionnée ci-dessus, ainsi qu'une référence mutable au vecteur chromosomique new_chromosomes. Il s'agit du vecteur de chromosomes obtenu après l'étape de mutation. La mise en œuvre de la méthode pre_birth () devrait supprimer les chromosomes de ce vecteur qui ne sont évidemment pas adaptés à l'état du problème.

Pour le cas où la fonction du vecteur de nombres à virgule flottante est optimisée, le module optlib :: génétique :: pre_birth :: vec_float contient la structure CheckChromoInterval , conçue pour supprimer les chromosomes s'ils sont un vecteur de nombres à virgule flottante et un élément du vecteur ne tombe pas dans l'intervalle spécifié.

Le constructeur de la structure CheckChromoInterval est le suivant:

 pub fn new(intervals: Vec<(G, G)>) -> CheckChromoInterval<G> { ... } 

Ici, le constructeur prend un vecteur de tuples avec deux éléments - la valeur minimale et maximale pour chaque élément du chromosome. Ainsi, la taille du vecteur d'intervalles doit coïncider avec la taille du vecteur chromosomique des individus. Dans l'exemple ci-dessus, un vecteur de 15 tuples (-500.0f32, 500.0f32) a été utilisé comme intervalles.

Sélection Sélection - Sélection

Après une sélection préliminaire des chromosomes, des individus sont créés et placés dans la population (Structure de la population ). Dans le processus de création d'individus pour chacun d'eux, la valeur de la fonction objectif est calculée. Au stade de la sélection, il faut détruire un certain nombre d'individus pour que la population ne croisse pas indéfiniment. Pour cela, le trait Selection est utilisé, qui est déclaré comme suit:

 pub trait Selection<T: Clone> { fn kill(&mut self, population: &mut Population<T>); } 

Un objet qui implémente le trait Selection dans la méthode kill () doit appeler la méthode kill () de la structure individuelle (individu) pour chaque individu de la population qui doit être détruit.

Pour contourner tous les individus d'une population, vous pouvez utiliser un itérateur qui renvoie la méthode IterMut () de la structure de la population.

Puisqu'il est souvent nécessaire d'appliquer plusieurs critères de sélection, lors de la création de la structure GeneticOptimizer , le constructeur accepte un vecteur d'objets de type Sélection.

Comme pour les autres étapes de l'algorithme génétique, le module optlib :: génétique :: sélection propose déjà plusieurs implémentations de l'étape de sélection.

• KillFitnessNaN - détruit les individus dont la valeur de la fonction objectif est NaN ou Inf.
• LimitPopulation - détruit un tel nombre de pires individus afin que la taille de la population ne dépasse pas une taille donnée.
• optlib :: génétique :: sélection :: vec_float :: CheckChromoInterval - dans le cas où la fonction du vecteur de nombres à virgule flottante est optimisée, elle détruit les individus dont la valeur chromosomique ne rentre pas dans les intervalles donnés. Cette structure fonctionne de manière similaire à la structure optlib :: génétique :: pre_birth :: vec_floatCheckChromoInterval de l' étape précédente de l'algorithme génétique.

Trait StopChecker - critère d'arrêt

Après l'étape de sélection, vous devez vérifier s'il est temps d'arrêter l'algorithme génétique. Comme déjà mentionné ci-dessus, à ce stade, vous pouvez également utiliser différents algorithmes d'arrêt. Pour l'interruption de l'algorithme, l'objet est responsable de la mise en œuvre du trait StopChecker , qui est déclaré comme suit:

 pub trait StopChecker<T: Clone> { fn can_stop(&mut self, population: &Population<T>) -> bool; } 

Ici, la méthode can_stop () devrait retourner true si l'algorithme peut être arrêté, sinon cette méthode devrait retourner false.

Le module optlib :: génétique :: stopchecker contient plusieurs structures avec des critères d'arrêt de base et deux structures pour créer des combinaisons à partir d'autres critères:

• MaxIterations - critère de rupture par numéro de génération. L'algorithme génétique s'arrêtera après un nombre donné d'itérations (générations).
• GoalNotChange - un critère de rupture selon lequel l'algorithme doit s'arrêter si une nouvelle solution ne peut pas être trouvée pour un nombre donné d'itérations. Ou en d'autres termes, si pour un nombre donné de générations, il n'y a pas d'individus plus performants.
• Seuil - un critère d'arrêt selon lequel l'algorithme génétique est interrompu si la valeur de la fonction objective de la meilleure solution à l'heure actuelle est inférieure à la valeur seuil spécifiée.
• CompositeAll — , ( - StopChecker). , - , .
• CompositeAny — , ( - StopChecker). , - , .

Logger —

Logger , , , . Logger :

 pub trait Logger<T: Clone> { ///       fn start(&mut self, _population: &Population<T>) {} ///     , ///           fn resume(&mut self, _population: &Population<T>) {} ///         /// (    ) fn next_iteration(&mut self, _population: &Population<T>) {} ///      fn finish(&mut self, _population: &Population<T>) {} } 

optlib::genetic::logging , Logger:

• StdoutResultOnlyLogger — ;
• VerboseStdoutLogger — .
• TimeStdoutLogger — , .

Le constructeur de la structure GeneticOptimizer , comme dernier argument, accepte un vecteur de types de caractères Logger, qui vous permet de configurer de manière flexible la sortie du programme.

Fonctions de test d'algorithmes d'optimisation

Fonction Schweffel

Pour tester les algorithmes d'optimisation, de nombreuses fonctions ont été inventées avec de nombreux extrema locaux. Le module optlib :: testfunctions contient plusieurs fonctions sur lesquelles des algorithmes peuvent être testés. Au moment d'écrire ces lignes, le module optlib :: testfunctions ne contient que deux fonctions.

L'une de ces fonctions est la fonction Schweffel, qui a été décrite au tout début de l'article. Encore une fois, je rappelle que cette fonction s'écrit comme suit:

$$

$$F(\boldsymbol x) = 418.9829N - \sum_{i=1}^{N}x_i \sin (\sqrt{|x_i|})$$

x' = (420.9687, 420.9687, ...). .

optlib::testfunctions schwefel . N .

, , , , .

:

$$

$$F(\boldsymbol x) = \sum_{i=1}^{N} (x_i - n)^2$$

x' = (1.0, 2.0,… N). .

optlib::testfunctions paraboloid .

Conclusion

optlib , . ( optlib::genetic ), , , , .

optlib::genetic. . , , , , .

, . , ( , ..)

De plus, il est prévu d'ajouter de nouvelles fonctions analytiques (en plus de la fonction Schweffel) pour tester les algorithmes d'optimisation.

Encore une fois, je rappelle les liens associés à la bibliothèque optlib:

• Page sur github - https://github.com/Jenyay/rust-optimization
• Page sur crates.io - https://crates.io/crates/optlib
• Documentation - https://docs.rs/optlib

J'attends vos commentaires, ajouts et commentaires avec impatience.