Hachage polyvalent et parfait

Nous commençons la semaine avec du matériel utile dédié au lancement du cours "Algorithmes pour les développeurs" . Bonne lecture.



1. Présentation

Le hachage est un excellent outil pratique, avec une théorie intéressante et subtile. En plus d'utiliser les données comme structure de vocabulaire, le hachage se trouve également dans de nombreux domaines différents, y compris la cryptographie et la théorie de la complexité. Dans cette conférence, nous décrivons deux concepts importants: le hachage universel (également connu sous le nom de famille universelle de fonctions de hachage) et le hachage idéal.

Le matériel mis en évidence dans cette conférence comprend:

• Le cadre formel et l'idée générale du hachage.
• Hachage universel.
• Hachage parfait.

2. Introduction

Nous allons considérer le problème principal avec le dictionnaire que nous avons discuté auparavant, et considérer deux versions: statique et dynamique:

• Statique : étant donné un grand nombre d'éléments S, nous voulons le stocker de manière à pouvoir effectuer rapidement une recherche.
• Par exemple, un dictionnaire fixe.
• Dynamique : nous avons ici une séquence de demandes d'insertion, de recherche et éventuellement de suppression. Nous voulons faire tout cela efficacement.

Pour le premier problème, nous pourrions utiliser un tableau trié et une recherche binaire. Pour le second, nous pourrions utiliser un arbre de recherche équilibré. Cependant, le hachage fournit une approche alternative, qui est souvent le moyen le plus rapide et le plus pratique pour résoudre ces problèmes. Par exemple, supposons que vous écrivez un programme de recherche AI ​​et que vous souhaitiez stocker des situations que vous avez déjà résolues (positions sur le tableau ou éléments de l'espace d'état) afin de ne pas répéter les mêmes calculs lorsque vous les rencontrez à nouveau. Le hachage permet de stocker facilement ces informations. Il existe également de nombreuses applications en cryptographie, réseaux, théorie de la complexité.

3. Bases du hachage

Le paramètre formel de hachage est le suivant.

• Les clés appartiennent à un grand ensemble de U. (Par exemple, imaginez que U est une collection de toutes les chaînes avec une longueur maximale de 80 caractères ascii.)
• Nous avons vraiment besoin de quelques clés S en U (les clés peuvent être statiques ou dynamiques). Soit N = | S |. Imaginez que N est beaucoup plus petit que la taille de U. Par exemple, S est l'ensemble des noms d'élèves dans une classe qui est beaucoup plus petit que 128 ^ 80.
• Nous allons effectuer des insertions et des recherches en utilisant un tableau A d'une certaine taille M et une fonction de hachage h: U → {0, ..., M - 1}. Étant donné l'élément x, l'idée de hachage est que nous voulons le stocker dans A [h (x)]. Notez que si U était petit (par exemple, des chaînes de 2 caractères), vous pourriez simplement enregistrer x dans A [x], comme dans le tri par blocs. Le problème est que U est grand, nous avons donc besoin d'une fonction de hachage.
• Nous avons besoin d'une méthode pour résoudre les collisions. Une collision se produit lorsque h (x) = h (y) pour deux clés différentes x et y. Dans cette conférence, nous traiterons les collisions en définissant chaque élément de A comme une liste chaînée. Il existe un certain nombre d'autres méthodes, mais pour les problèmes sur lesquels nous nous concentrerons ici, c'est la plus appropriée. Cette méthode est appelée méthode de chaînage. Pour insérer un élément, nous le mettons simplement en haut de la liste. Si h est une bonne fonction de hachage, alors nous espérons que les listes seront petites.

L'un des avantages du hachage est que toutes les opérations de dictionnaire sont incroyablement faciles à implémenter. Pour rechercher la clé x, calculez simplement l'indice i = h (x) puis parcourez la liste dans A [i] jusqu'à ce que vous la trouviez (ou quittez la liste). Pour insérer, placez simplement un nouvel élément en haut de sa liste. Pour supprimer, il vous suffit d'effectuer l'opération de suppression dans la liste liée. Passons maintenant à la question: de quoi avons-nous besoin pour obtenir de bonnes performances?

Propriétés souhaitables. Propriétés clés souhaitables pour un bon schéma de hachage:

1. Les clés sont bien dispersées afin que nous n'ayons pas trop de collisions, car les collisions affectent le temps de recherche et de suppression.
2. M = O (N): en particulier, nous aimerions que notre circuit atteigne la propriété (1) sans que la taille du tableau M soit beaucoup plus grande que le nombre d'éléments N.
3. La fonction h doit être calculée rapidement. Dans notre analyse d'aujourd'hui, nous considérerons le temps pour calculer h (x) comme une constante. Cependant, il convient de rappeler que cela ne devrait pas être trop compliqué car cela affecte le temps d'exécution global.

Compte tenu de cela, le temps de recherche pour l'élément x est O (la taille de la liste est A [h (x)]). Il en va de même pour les suppressions. Les insertions prennent O (1), quelle que soit la longueur des listes. Nous voulons donc analyser la taille de ces listes.

Intuition de base: une façon de bien répartir les éléments est de les répartir de manière aléatoire. Malheureusement, nous ne pouvons pas simplement utiliser le générateur de nombres aléatoires pour décider où diriger l'élément suivant, car nous ne pourrons plus jamais le retrouver. Donc, nous voulons que h soit quelque chose de «pseudo-aléatoire» dans un sens formel.

Nous allons maintenant présenter de mauvaises nouvelles, puis de bonnes nouvelles.

Énoncé 1 (mauvaise nouvelle) Pour toute fonction de hachage h si | U | ≥ (N −1) M +1, il y a un ensemble S d'éléments N qui ont tous haché au même endroit.

Preuve: par le principe de Dirichlet. En particulier, pour considérer les contrepoints, si chaque emplacement n'avait pas plus de N - 1 éléments de U qui le hachaient, alors U pourrait avoir une taille ne dépassant pas M (N - 1).

C'est en partie pourquoi le hachage semble si mystérieux - comment peut-on affirmer que le hachage est bon si, pour une fonction de hachage, vous pouvez penser à des moyens de l'empêcher? Une réponse est qu'il existe de nombreuses fonctions de hachage simples qui fonctionnent bien dans la pratique pour les ensembles typiques S. Mais que faire si nous voulons une bonne garantie du pire des cas?

Voici l'idée clé: utilisons la randomisation dans notre construction h, similaire au tri rapide randomisé. (Inutile de dire que h sera une fonction déterministe). Nous montrerons que pour toute séquence d'opérations d'insertion et de recherche (nous n'avons pas besoin de supposer que l'ensemble des éléments insérés S est aléatoire), si nous choisissons h de cette manière probabiliste, les performances de h dans cette séquence seront bonnes en prévision. Ainsi, c'est la même garantie que dans le tri rapide ou les pièges randomisés. En particulier, c'est l'idée du hachage universel.

Une fois que nous aurons développé cette idée, nous l'utiliserons pour une application particulièrement agréable appelée «hachage parfait».

4. Hachage universel

Définition 1. Un algorithme aléatoire H pour construire des fonctions de hachage h: U → {1, ..., M}
universel si pour tout x! = y dans U nous avons



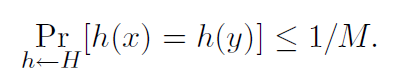
On peut aussi dire que l'ensemble H des fonctions de hachage est une famille universelle de fonctions de hachage si la procédure «aléatoirement sélectionner h ∈ H» est universelle. (Ici, nous identifions l'ensemble des fonctions avec une distribution uniforme sur l'ensemble.)

Théorème 2. Si H est universel, alors pour tout ensemble S ⊆ U de taille N, pour tout x ∈ U (par exemple, que nous pourrions rechercher), si nous construisons h au hasard conformément à H, le nombre attendu de collisions entre x et d'autres éléments en S pas plus que N / M.

Preuve: chaque y ∈ S (y! = X) a au plus 1 / M de chance de collision avec x par la définition de «universel». Alors

• Soit Cxy = 1 si x et y entrent en collision, et 0 sinon.
• Soit Cx le nombre total de collisions pour x. Donc, Cx = Py∈S, y! = X Cxy.
• Nous savons que E [Cxy] = Pr (x et y entrent en collision) ≤ 1 / M.
• Ainsi, en linéarité de l'espérance, E [Cx] = Py E [Cxy] <N / M.

Nous obtenons maintenant le corollaire suivant.

Corollaire 3. Si H est universel, alors pour toute séquence d'opérations d'insertion, de recherche et de suppression L, dans laquelle il ne peut y avoir plus de M éléments dans un système à la fois, le coût total attendu des opérations L pour un h aléatoire ∈ H n'est que de O (L) (affichage de l'heure pour calculer h comme constantes).

Preuve: pour toute opération donnée de la séquence, son coût attendu est constant par le théorème 2, donc le coût total attendu des opérations L est O (L) en linéarité des attentes.

Question: peut-on réellement construire un H universel? Sinon, tout cela est assez inutile. Heureusement, la réponse est oui.

4.1. Création d'une famille de hachage universelle: méthode matricielle

Supposons que les clés aient une longueur de u bits. Disons que la taille de la table M est égale au degré 2; par conséquent, l'index est long de b bits avec M = 2b.

Ce que nous allons faire est de choisir h comme matrice aléatoire 0/1 b-by-u et de définir h (x) = hx, où nous ajoutons le mod 2. Ces matrices sont courtes et épaisses. Par exemple:



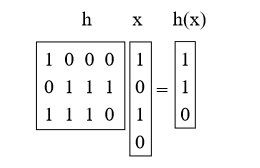
Proposition 4. Pour x! = Y Prh [h (x) = h (y)] = 1 / M = 1 / 2b.

Preuve: tout d'abord, que signifie multiplier h par x? Nous pouvons penser à cela comme l'ajout de certaines colonnes h (en faisant l'addition vectorielle mod 2), où 1 bit en x indique celles à ajouter. (par exemple, nous avons ajouté les 1ère et 3ème colonnes de h ci-dessus)

Prenez maintenant une paire de clés arbitraire x, y telle que x! = Y. Ils devraient être différents quelque part, alors disons qu'ils diffèrent dans la i-ème coordonnée, et pour plus de concrétisation, nous disons xi = 0 et yi = 1. Imaginez que nous avons d'abord sélectionné tous les h sauf la i-ème colonne. Pour les autres échantillons de la ième colonne, h (x) est fixe. Cependant, chacun des 2b réglages différents de la ième colonne donne une valeur différente de h (y) (en particulier, chaque fois que nous tournons un peu dans cette colonne, nous transformons le bit correspondant en h (y)). Il y a donc exactement 1 / 2b de chance que h (x) = h (y).

Il existe d'autres méthodes pour construire des familles de hachage universelles, qui sont également basées sur la multiplication des nombres premiers (voir la section 6.1).

La question suivante que nous considérerons: si nous corrigeons l'ensemble S, pouvons-nous trouver une fonction de hachage h telle que toutes les recherches auront un temps constant? La réponse est oui, ce qui mène au sujet du hachage parfait.

5. Hachage parfait

Nous disons qu'une fonction de hachage est idéale pour S si toutes les recherches ont lieu dans O (1). Voici deux façons de créer des fonctions de hachage parfaites pour un ensemble donné S.

5.1 Méthode 1: une solution dans l'espace O (N2)

Disons que nous voulons avoir une table dont la taille est quadratique en taille N de notre dictionnaire S. Alors, voici une méthode simple pour construire une fonction de hachage idéale. Soit H universel et M = N2. Ensuite, choisissez simplement un h aléatoire de H et essayez-le! La déclaration est qu'il y a au moins 50% de chances qu'elle n'ait pas de collisions.

Proposition 5. Si H est universel et M = N2, alors Prh∼H (pas de collisions dans S) ≥ 1/2.

Preuve:

• Combien de paires (x, y) y a-t-il dans S? La réponse est:
• Pour chaque paire, la probabilité de leur collision est ≤ 1 / M par définition d'universalité.
• Donc Pr (il y a collision) ≤ / M <1/2.

C'est comme l'autre côté du «paradoxe d'anniversaire». Si le nombre de jours est beaucoup plus grand que le nombre de personnes au carré, il y a une chance raisonnable qu'aucun couple n'ait le même anniversaire.

Donc, nous choisissons simplement un h aléatoire de H, et si des collisions surviennent, nous choisissons simplement un nouveau h. En moyenne, nous n'aurons besoin de le faire que deux fois. Maintenant, que se passe-t-il si nous voulons utiliser uniquement l'espace O (N)?

5.2 Méthode 2: une solution dans l'espace O (N)

La question de savoir s'il est possible d'obtenir un hachage parfait dans l'espace O (N) est ouverte depuis un certain temps: "Faut-il trier les tables?" Autrement dit, pour un ensemble fixe, vous ne pouvez obtenir un temps de recherche constant qu'avec un espace linéaire? Il y a eu une série de tentatives de plus en plus complexes, jusqu'à ce qu'il soit finalement résolu en utilisant la bonne idée des fonctions de hachage universelles dans un schéma à deux niveaux.

La méthode est la suivante. Tout d'abord, nous allons hacher dans une table de taille N en utilisant un hachage universel. Cela entraînera des collisions (sauf si nous avons de la chance). Cependant, nous remanions chaque panier en utilisant la méthode 1, en ajustant la taille du panier pour obtenir zéro collision. Ainsi, le schéma consiste dans le fait que nous avons une fonction de hachage du premier niveau h et une table A du premier niveau, puis N fonctions de hachage du deuxième niveau h1, ..., hN et N de la deuxième table de niveau A1, ..., A.N ... Pour trouver l'élément x, nous calculons d'abord i = h (x), puis trouvons l'élément dans Ai [hi (x)]. (Si vous faisiez cela en pratique, vous pourriez définir le drapeau de sorte que vous ne fassiez la deuxième étape que s'il y avait vraiment des conflits avec l'index i, sinon vous mettriez simplement x lui-même dans A [i], mais disons ne nous en soucions pas ici.)

Disons qu'une fonction de hachage h hache n éléments de S à l'emplacement i. Nous avons déjà prouvé (en analysant la méthode 1) que nous pouvons trouver h1, ..., hN, de sorte que l'espace total utilisé dans les tables secondaires est Pi (ni) 2. Il reste à montrer que nous pouvons trouver une fonction de premier niveau h telle que Pi (ni) 2 = O (N). En fait, nous allons montrer ce qui suit:

Théorème 6. Si nous choisissons le point de départ h dans l'ensemble universel H, alors

Pr[X i (ni)2 > 4N] < 1/2. 

Preuve. Prouvons cela en montrant que E [Pi (ni) 2] <2N. Cela implique ce que nous voulons de l'inégalité de Markov. (S'il y avait même une probabilité de 1/2 que la somme puisse être supérieure à 4N, alors ce seul fait signifierait que l'attente devrait être supérieure à 2N. Ainsi, si l'attente est inférieure à 2N, la probabilité d'échec devrait être inférieure 1/2.)

Maintenant, l'astuce est qu'une façon de calculer ce montant est de compter le nombre de paires ordonnées qui ont une collision, y compris les collisions avec soi-même. Par exemple, si le panier a {d, e, f}, alors d aura un conflit avec chacun de {d, e, f}, e aura un conflit avec chacun de {d, e, f}, et f aura un conflit avec chacun de {d, e, f}, nous obtenons donc 9. Donc, nous avons:

 E[X i (ni)2] = E[X x X y Cxy] (Cxy = 1 if x and y collide, else Cxy = 0) = N +X x X y6=x E[Cxy] ≤ N + N(N − 1)/M (where the 1/M comes from the definition of universal) < 2N. (since M = N) 

Donc, nous essayons simplement un h aléatoire de H jusqu'à ce que nous en trouvions un tel que Pi n2 i <4N, puis en fixant cette fonction h, nous trouvons N fonctions de hachage secondaires h1, ..., hN comme dans la méthode 1.

6. Discussion supplémentaire

6.1 Une autre méthode de hachage universelle

Voici une autre méthode pour construire des fonctions de hachage universelles, qui est légèrement plus efficace que la méthode matricielle donnée précédemment.

Dans la méthode matricielle, nous avons considéré la clé comme un vecteur de bits. Dans cette méthode, nous considérerons plutôt la clé x comme un vecteur d'entiers [x1, x2, ..., xk] avec la seule exigence que chaque xi soit dans la plage {0, 1, ..., M-1}. Par exemple, si nous hachons des chaînes de longueur k, alors xi peut être le ième caractère (si la taille de notre table est au moins 256) ou la ième paire de caractères (si la taille de notre table est au moins 65536). De plus, nous exigerons que la taille de notre table M soit un nombre premier. Pour sélectionner la fonction de hachage h, nous sélectionnons k nombres aléatoires r1, r2, ..., pk parmi {0, 1, ..., M - 1} et déterminons:

 h(x) = r1x1 + r2x2 + . . . + rkxk mod M. 

La preuve que cette méthode est universelle est construite de la même manière que la preuve de la méthode matricielle. Soit x et y deux clés différentes. Nous voulons montrer que Prh (h (x) = h (y)) ≤ 1 / M. Puisque x! = Y, il doit y avoir un cas où il existe un indice i tel que xi! = Yi. Imaginez maintenant que vous avez d'abord sélectionné tous les nombres aléatoires rj pour j! = I. Soit h ′ (x) = Pj6 = i rjxj. Donc, en choisissant ri, nous obtenons h (x) = h ′ (x) + rixi. Cela signifie que nous avons un conflit entre x et y exactement quand

 h′(x) + rixi = h′(y) + riyi mod M, or equivalently when ri(xi − yi) = h′(y) − h′(x) mod M. 

Puisque M est premier, la division par une valeur non nulle de mod M est valide (chaque entier de 1 à M -1 a un modulo inverse M multiplicatif), ce qui signifie qu'il existe exactement une valeur ri modulo M pour laquelle l'équation ci-dessus est vraie vrai, à savoir ri = (h ′ (y) - h ′ (x)) / (xi - yi) mod M. Ainsi, la probabilité de cet incident est exactement de 1 / M.

6.2 Autres utilisations du hachage

Supposons que nous ayons une longue séquence d'éléments et que nous voulons voir le nombre d'éléments différents dans la liste. Existe-t-il un bon moyen de procéder?

Une façon consiste à créer une table de hachage, puis à effectuer un passage dans la séquence en effectuant une recherche pour chaque élément, puis en l'insérant s'il ne figure pas déjà dans la table. Le nombre d'éléments individuels est simplement le nombre d'inserts.

Et maintenant, que se passe-t-il si la liste est vraiment énorme et que nous n'avons pas d'endroit où la stocker, mais une réponse approximative nous convient. Par exemple, imaginez que nous sommes un routeur et observons le nombre de paquets qui passent, et nous voulons (approximativement) voir combien d'adresses IP source différentes existent.

Voici une bonne idée: disons que nous avons une fonction de hachage h qui se comporte comme une fonction aléatoire, et imaginons que h (x) est un nombre réel de 0 à 1. Une chose que nous pouvons faire est de simplement garder une trace du minimum la valeur de hachage a été produite jusqu'à présent (nous n'avons donc pas de table du tout). Par exemple, si les clés sont 3,10,3,3,12,10,12 et h (3) = 0,4, h (10) = 0,2, h (12) = 0,7, alors nous obtenons 0, 2.

Le fait est que si nous sélectionnons N nombres aléatoires dans [0, 1], la valeur minimale attendue sera 1 / (N + 1). De plus, il y a de fortes chances qu'il soit assez proche (nous pouvons améliorer notre estimation en exécutant plusieurs fonctions de hachage et en prenant la médiane des plus bas).

Question: pourquoi utiliser une fonction de hachage, et pas seulement choisir un nombre aléatoire à chaque fois? C'est parce que nous nous soucions du nombre d'éléments différents, et pas seulement du nombre total d'éléments (ce problème est beaucoup plus simple: il suffit d'utiliser un compteur ...).

Amis, cet article vous a-t-il été utile? Écrivez dans les commentaires et rejoignez la journée portes ouvertes , qui se tiendra le 25 avril.