Bonjour cher lecteur! Je vous présente la traduction de l'anglais de l'article «Physique, la prochaine frontière» de Chris Hecker.

Moi, un développeur Java novice, était confronté au fait que les matériaux pour créer un moteur physique dans le jeu ne sont présentés qu'en anglais, donc cet article a été traduit. Il y aura trois autres articles dans la série, je les posterai dès que possible. Bonne lecture!

De nouvelles frontières en physique

Il ne fait aucun doute que chaque année, les graphismes du jeu deviennent plus réalistes. Aujourd'hui déjà, tout le monde crée (ou du moins montre des captures d'écran) des mondes 3D avec des cartes de texture, et lorsque suffisamment de personnes assidues se réunissent pour travailler sur un projet, chaque développeur peut dessiner des milliards de polygones de textures et d'ombres réalistes par seconde. Sur le plan technique, que reste-t-il à faire pour créer un jeu de haut niveau? Est-ce que chaque développeur avec une copie du livre «Apprenez à utiliser le matériel 3D en 21 jours» pourra-t-il créer un jeu vraiment impressionnant?

Pas du tout. Les développeurs haut de gamme continueront d'élever la barre dans de nombreuses technologies différentes (telles que la complexité de l'interface graphique, l'intelligence artificielle et la mise en réseau). Bien sûr, tout cela est très important, nous ne pouvons même pas en discuter sérieusement sans préciser les détails. Néanmoins, il existe une technologie applicable à tout, qui, à mon avis, deviendra un facteur décisif dans un proche avenir: la physique.

Prenons l'exemple suivant: vous souvenez-vous de ces énormes engrenages tournants dans l'un des premiers niveaux de Duke Nukem 3D?



Figure 1. Capture d'écran du jeu "Duke Nukem 3D"

Imaginez simplement que leur rotation serait décrite non pas par une animation cyclique, mais par un véritable moteur physique. Soudain, les engrenages deviennent plus qu'une décoration de jeu, tout comme l'un d'eux dévie d'un angle donné et roule dans le couloir derrière vous, comme dans les films d'Indiana Jones. Ou imaginez qu'après avoir tiré un équipement d'un lance-roquettes, il roulera dans le couloir et écrasera votre ami, qui s'est glissé derrière pour vous tuer! Les moteurs physiques rendent de telles situations réelles.

La simulation physique est ce qui rend le monde du jeu entier: grâce à elle, "ici" est situé ici, si vous comprenez ce que je veux dire. Toute magie dans les graphismes du monde ne permettra pas au joueur de plonger dans le processus de jeu s'il s'interpénètre dans un autre joueur, ou dans les murs du niveau, ou si la masse et le moment de la masse ne sont pas ressentis. Les animateurs de Disney ont trouvé que ce sentiment des masses était ce qui sépare une bonne animation d'une mauvaise animation. Selon l'épopée Disney Animation: The Illusion of Life de Frank Thomas et Ollie Johnston, les animateurs Disney, même juste accrochés une affiche dans le studio, devraient toujours se demander: "Y a-t-il beaucoup de poids, de profondeur et d'équilibre dans leur dessin?" ? "

Mais aujourd'hui, presque tous les jeux ont un moteur physique, non? Sans aucun doute, c'est ce qui empêche votre voiture de tomber au bord du monde du jeu, grâce à cela, vos personnages ne volent pas dans l'espace lorsqu'ils sautent, et cela jette votre bateau sur le côté lorsqu'une fusée explose à proximité. Cependant, la plupart des moteurs physiques des jeux modernes sont assez faibles. Ils ne font face qu'à la tâche d'empêcher la voiture de tomber au bord du monde, mais leurs capacités ne sont pas suffisantes pour amener le jeu à un nouveau niveau - où l'épave d'une voiture accidentée peut exploser directement sur la piste, provoquant un roulement de murs et d'autres voitures.

D'autres effets physiques qui sont souvent ignorés incluent: des simples effets de torsion à la suite d'une frappe tangente, aux personnages du jeu eux-mêmes gardant leur équilibre et se déplaçant, contrairement à ceux animés statiquement. Je crois que de nombreux développeurs ignorent ces possibilités car ils ne comprennent pas les mathématiques qui décrivent la physique ou étaient trop occupés à créer des textures pour l'apprendre. L'assaut du matériel pour travailler avec la 3D s'occupera de cette dernière, et je commence une nouvelle série d'articles. Le premier article s'occupera des formalités. À la fin de notre cycle, vous pouvez vous-même créer un moteur physique qui fera en sorte que les joueurs se sentent complètement immergés dans le gameplay, grâce à un réalisme incroyable, ou un surréalisme divertissant mais persistant.

Attention! Physique = mathématiques, pour mener à bien un projet intéressant, vous devrez utiliser les deux. Avant que cela ne vous fasse peur, permettez-moi de noter que les mathématiques qui décrivent la physique ne sont pas seulement élégantes et belles, elles ont également un caractère appliqué. Autrement dit, ce ne sont pas des mathématiques abstraites pour les mathématiques. Chaque équation que nous utilisons a une véritable signification physique. Nous créons des équations à partir d'un modèle physique, et en retour, les équations nous indiquent comment le modèle se comporte dans le temps.

Grande entreprise

La physique est un vaste domaine scientifique. Mais nous sommes vraiment intéressés par sa petite section appelée «dynamique», ou plus précisément, «dynamique des solides». La dynamique peut être définie en termes d'une section connexe - la cinématique (la doctrine du mouvement dans le temps). La cinématique ne se concentre pas sur les causes du mouvement ni sur la façon dont les corps se sont retrouvés là où ils sont, elle décrit simplement le mouvement. La dynamique, au contraire, décrit les forces et les masses qui contribuent aux valeurs de la cinématique à changer avec le temps. À quelle distance la balle de baseball volera si le temps de vol est de 10 secondes et sa vitesse initiale est de 50 kilomètres / heure, et la trajectoire - une ligne droite - est un problème cinématique; jusqu'où la balle de baseball volera dans le champ gravitationnel de la terre, si je la frappe avec une batte - c'est un problème dynamique.

La partie de la dynamique qui décrit les solides concerne les contraintes que nous ajoutons pour les objets simulés. La forme d'un corps solide ne change pas pendant la simulation - le corps est plus probablement en bois ou en métal qu'en gelée. Nous pouvons créer des figures articulées, par exemple, d'une personne, en construisant chaque partie de la figure à partir d'un corps solide et en créant des ligaments entre elles, mais nous ne compterons pas sur les os se pliant sous la tension ou des effets similaires. Cela nous permettra de simplifier nos équations sans perdre la qualité du comportement dynamique intéressant des corps.

Même si nous considérons une si petite partie de la dynamique, la dynamique d'un corps rigide nécessitera une série d'articles pour expliquer l'essence. Nous commençons notre voyage en étudiant les bases de la programmation informatique pour décrire le mouvement d'un corps rigide plan sous l'action des forces. Je répète constamment la «programmation informatique», car en plus des équations que nous écrivons pour la cinématique et la dynamique, nous apprendrons également à résoudre ces équations à l'aide de calculs avec des nombres à virgule flottante, ce qui est vital pour tout programmeur. Je dis «plat solide» parce que nous ne traiterons du monde à deux dimensions que dans le prochain article et au-delà. Les principes - et en fait plus que de simples équations - peuvent également être transférés dans le monde tridimensionnel, mais certainement tout est beaucoup plus simple dans le monde bidimensionnel, nous allons donc y étudier jusqu'à ce que nous soyons confiants d'entrer dans l'espace tridimensionnel. Dans de futurs articles, nous apprendrons à décrire l'effet de la rotation, le traitement des contacts des corps et, bien sûr, comment faire tout cela dans un monde en trois dimensions. Eh bien, assez de mots! Commençons!

Travailler avec un dérivé

Cela peut vous surprendre, mais vous ne pouvez vraiment pas déplacer un objet en le poussant simplement. Je sais, vous pensez que j'ai tort de prouver le contraire de moi en jetant ce magazine à la poubelle pour avoir écrit un tel non-sens, mais c'est vrai! Seule une pression sur un chargeur n'affectera jamais directement sa position dans l'espace. En fait, la pression n'affecte même pas directement sa vitesse. Ce que la pression affecte réellement, c'est l'accélération de la revue, et en fait c'est l'une des conclusions les plus importantes de l'histoire de la science.

Pour utiliser ce fait afin de faire quelque chose d'intéressant, nous devons d'abord parler de la relation de la position du corps avec la vitesse et l'accélération. En fait, toutes ces valeurs sont très étroitement liées (comme vous le savez probablement): la vitesse est un indicateur des changements dans les coordonnées du corps au fil du temps, et l'accélération est un indicateur des changements de vitesse. Le principal outil pour étudier les changements de ces quantités dans le temps est le calcul différentiel. Si vous comprenez cela, alors nous allons de l'avant. Je suppose que tu es bon en mathématiques. Nous n'utiliserons que des calculs scalaires et vectoriels simples (dérivés et intégrales), mais ce ne sera pas superflu si vous êtes familier avec les mathématiques dans leur ensemble. Pour référence: mon livre préféré sur l'informatique est le Calcul avec Géométrie Analytique de Thomas et Finney.

La coordonnée, la vitesse et l'accélération sont des cinématiques qui seront discutées dans cet article. L'emplacement d'un solide dans un monde à deux dimensions est, évidemment, une paire de coordonnées X et Y, qui désignent les coordonnées de l'espace d'un point donné du corps. La dérivée du vecteur de coordonnées est le vecteur vitesse, et il nous montre dans quelle direction le point se déplace (et le corps, si nous ignorons la rotation, qui se produit maintenant) et à quelle vitesse il se déplace. Le calcul vectoriel n'est que le calcul scalaire de chaque élément du vecteur, donc la dérivée de la coordonnée X est la vitesse corporelle par rapport à X, et ainsi de suite. Nous introduisons la notation suivante. Soit la coordonnée du corps le vecteur r et la vitesse le vecteur v ou le vecteur r avec un nombre premier. Nous obtenons l'équation:

$$

$${{dx} \ over {dt}} = v = r '$$

Équation 1

Si nous différencions le vecteur vitesse par rapport au temps, cela montrera comment le vecteur de coordonnées change avec le temps. L'accélération est déterminée par analogie. C'est la première dérivée de la vitesse ou la deuxième dérivée du vecteur de coordonnées:

$$

$${{d ^ 2 r} \ over {dt ^ 2}} = r '' = {{dr '} \ over {dt}} = {{dv} \ over {dt}} = v' = a$$

Équation 2

L'intégrale de l'accélération nous donnera de la vitesse, et en intégrant l'accélération deux fois, nous obtenons les coordonnées.

Ces relations en cinématique montrent que nous pouvons trouver l'accélération d'un objet, nous pouvons l'intégrer dans le temps pour obtenir la vitesse et la coordination. Comme nous le verrons plus loin, nous nous tournerons à plusieurs reprises vers l'intégration dans notre code de simulation et calculerons une nouvelle position pour notre solide pour chaque image. Hourra l'animation!

Voici un exemple simple d'un monde unidimensionnel que nous pouvons intégrer analytiquement. Convenons que nous voulons trouver le changement de coordonnées de la fin de la dernière image au moment de l'image actuelle pour dessiner la position actuelle. Ensuite, nous disons que l'accélération de notre solide était égale à 5 unités arbitraires / seconde ^ 2. Nous utiliserons le temps écoulé depuis la fin de la dernière trame comme variable t (dans l'élément d'intégration dt).

$$

$$v (t) = ∫adt = ∫5dt = 5t + C$$

Équation 3

Les équations ci-dessus montrent que la vitesse est fonction du temps écoulé depuis la dernière image. Nous avons trouvé la constante d'intégration, C, qui est égale à la vitesse initiale au début de la période d'intégration (à t = 0).

$$

$$v (0) = 5 (0) + C$$

$$

$$v_0 = {C}$$

Équation 4

$$

$$v (t) = 5t + v_0 {}$$

Maintenant, nous intégrons notre équation de vitesse pour trouver la coordonnée (encore une fois, n'oubliez pas la constante d'intégration):

$$

$$r (t) = ∫v (t) dt = ∫5t + v_0 dt = {{5} \ over {2}} t ^ 2 + v_0 t + r_0$$

Équation 5

Sur la base de l'équation 5, nous ne pouvons trouver la position actuelle que par une accélération donnée si nous connaissons la coordonnée et la vitesse initiales (que nous prendrons à partir de la dernière image) et le temps écoulé. La variable d'entrée est le temps et la valeur de la fonction est la position actuelle. Nous indiquerons également le temps dans l'équation 4 afin de calculer la vitesse finale afin de pouvoir l'utiliser comme condition initiale pour la prochaine image.

Que la force soit avec toi

Nous comprenons maintenant que nous devons régler correctement l'accélération pour intégrer les équations cinématiques afin d'obtenir l'animation. La sortie des enceintes sur scène. Rappelez-vous, comme je l'ai dit, en appuyant sur quelque chose, vous n'affectez directement que l'accélération du corps? Eh bien, «exercer une pression» n'est qu'un euphémisme pour l'expression «appliquer une force» - l'une des deux variables clés de la dynamique - et maintenant nous pouvons nous tourner vers Newton pour découvrir comment les forces affectent l'accélération. La deuxième loi de Newton relie la force F à la dérivée de la masse - la deuxième amplitude de la dynamique - multipliée par la vitesse. Le produit de la masse et de la vitesse est appelé "l'élan du corps", noté p:

$$

$$F = p '= {{dp} \ over {dt}} = {{d (mv)} \ over {dt}} = mv' = ma$$

Équation 6

La masse est une constante pour les vitesses avec lesquelles nous travaillons actuellement, cela découle de la dérivée de l'équation 6, et nous avons obtenu l'équation bien connue F = ma (même si je suis sûr que Newton a initialement déterminé la force à travers la dérivée de l'élan).

Si nous ne nous occupions que de points matériels, l'équation 6 est ce dont nous avons besoin en dynamique. Pour une force donnée d'un point matériel donné, l'accélération est trouvée en divisant la force par la masse. Cela nous donne une accélération, ce qui aidera à résoudre l'équation du mouvement de l'exemple ci-dessus. Néanmoins, nous avons affaire à des solides dont la masse est répartie sur une certaine zone (volume, en ce qui concerne le monde tridimensionnel), nous avons donc encore besoin de travailler.

Tout d'abord, considérons un solide comme un ensemble de masses ponctuelles. Nous définirons l'impulsion totale, pT, pour un solide, comme la somme des impulsions de tous les points qui composent le corps (j'utilise l'indexation supérieure, car je veux montrer plus clairement quelles valeurs quantitatives appartiennent à ces points):

$$

$$p ^ T = \ sum_ {i} {m ^ i v ^ i}$$

Équation 7

Nous pouvons grandement simplifier l'analyse de la dynamique d'un corps rigide en introduisant le concept de centre de masse (CM). Un vecteur dirigé vers le centre de masse est une somme linéaire de vecteurs dirigés à partir de tous les points de masse d'un corps solide divisé par la masse de tout le corps, M:

$$

$$r ^ {CM} = {\ sum_ {i} {m ^ i r ^ i} \ sur {M}}$$

Équation 8

En utilisant la définition du centre de masse, nous pouvons simplifier l'équation 7 en multipliant les deux côtés de l'équation 8 par M, en les différenciant, puis en substituant le résultat dans l'équation 7:

$$

$${{d (Mr ^ {CM})} \ over {dt}} = {\ sum_ {i} {} {{d (m ^ ir ^ i) \ over dt}}} = {\ sum_ {i} {} {m ^ iv ^ i}} = p ^ T$$

Équation 9

Le côté droit de l'équation 9 est l'élan total tel que défini dans l'équation 7. Regardons maintenant le côté gauche de l'équation: c'est la vitesse au centre de la masse multipliée par la masse du corps entier. Déplacez le côté droit vers la gauche et obtenez:

$$

$$p ^ T = {{d (Mr ^ {CM})} \ over {dt}} = Mv ^ {CM}$$

Équation 10

Il résulte de l'équation 10 que la quantité de mouvement linéaire est égale à la masse totale multipliée par la vitesse dirigée à partir du centre de masse, il n'est donc pas nécessaire de faire la somme dans l'équation 7 pour trouver la quantité de mouvement si nous connaissons la masse du corps et la direction du vecteur vitesse du centre de masse. De plus, tous les résultats finaux des calculs trouvent les intégrales pour tout le corps, mais le centre de masse existe et simplifie considérablement la détermination de la quantité de mouvement totale à partir de l'équation 10, donc nous ne pouvons pas nous inquiéter - pour trouver la quantité de mouvement linéaire, nous pouvons considérer le corps comme un point matériel avec une vitesse et une masse données.

Par analogie, la force totale est une dérivée de la quantité de mouvement totale, de sorte que le concept du centre de masse peut être utilisé pour simplifier l'équation de la force:

$$

$$F ^ T = p ^ T = Mv '^ {CM} = Ma ^ {CM}$$

Équation 11

Bref, il résulte de l'équation 11 que l'on peut considérer toutes les forces interagissant avec un solide, comme si leur vecteur somme avait un effet sur le point du centre de masse, qui contient la masse de tout le corps. Nous divisons la force (lire la gravité) par M afin de trouver l'accélération du centre de masse, puis intégrons l'accélération dans le temps afin d'obtenir la vitesse et les coordonnées du corps. Parce que nous ignorons les effets de la rotation jusqu'au prochain article; nous avons déjà toutes les équations dont nous avons besoin pour décrire la dynamique d'un corps rigide. Notez que l'équation 11 ne contient pas d'informations sur la direction des forces appliquées au corps. Cela apparaîtra lorsque nous traiterons de l'élan linéaire et du centre de masse, et nous appliquons simplement des forces au CM pour trouver l'accélération du centre de masse. Lorsque nous calculerons la rotation du corps sous l'influence de ces forces dans l'article suivant, nous verrons comment la coordonnée de l'application de la force est utilisée.

Ode à la joie

À ce stade, nous pouvons considérer un autre exemple d'intégration analytique, en utilisant l'équation 11 pour trouver l'accélération du centre de masse au lieu d'une valeur choisie arbitrairement = 5. Néanmoins, nous sommes confrontés à un problème grave, car l'intégration analytique n'a généralement pas de valeur appliquée, car c'est trop compliqué, nous allons donc nous concentrer sur la soi-disant intégration numérique des équations différentielles ordinaires (ODE). Wow, maintenant cela ressemble à de vrais maths! Une fois que vous aurez appris cela, il sera temps de relever la barre. Heureusement, l'intégration numérique des ODE n'est pas aussi difficile que cela puisse paraître à première vue! Afin de comprendre ce que cela signifie, nous passons des mots aux actes!

Ainsi, une équation différentielle est une équation qui contient des dérivées de quantités dépendantes en plus de la fonction elle-même, des variables et des paramètres indépendants. C'est verbeux, mais voici un exemple de force variant dans le temps dans un monde unidimensionnel: F = 2t, F est une quantité dépendante et t est une quantité indépendante. La valeur de F n'est déterminée que par F. Que l'équation de la force ne dépende que de la vitesse de notre corps. La force de la résistance de l'air augmente avec l'augmentation de la vitesse de l'avion.Revenons à l'exemple dans le monde unidimensionnel, et si F = -v signifie que la force de friction ralentit notre corps proportionnellement à la vitesse? Nous avons un problème, car nous résolvons l'équation comme suit: F = ma = -v et, en divisant par m, nous obtenons (rappelez-vous que l'accélération est une dérivée de la vitesse):

$$

$$a = {{dv}\over {dt}} = {-v\over m}$$

Équation 12

Cette équation différentielle (l'équation de vitesse contient la dérivée de vitesse dans l'équation 12) est appelée équation différentielle ordinaire, car elle ne contient que des dérivées ordinaires de quantités dépendantes (par opposition aux dérivées partielles, qui constituent des équations différentielles partielles [PDE], dont nous ne sommes pas nous parlerons).

Passons maintenant à la partie suivante de notre phrase: l'intégration. Comment avons-nous intégré auparavant dv / dt pour trouver v dans les conditions de cette équation?

Cela semblera incroyable, mais presque toutes les équations en physique sont des équations différentielles, donc les ODE ont été bien étudiées. Les équations différentielles peuvent si souvent être trouvées en physique, car souvent le taux de variation d'une quantité quantitative dépend de la quantité elle-même. Par exemple, nous avons déjà noté que le freinage (l'ampleur d'un changement de vitesse), y compris la vitesse de résistance à l'air, dépend de la vitesse. Autres exemples tirés de la physique: refroidissement (le taux de perte de chaleur dépend de la température actuelle) et désintégration radioactive (le taux de désintégration dépend de la quantité de matière radioactive présente).

Le dernier mot de notre phrase - numérique - est notre salut. Je dis cela parce que la théorie de l'intégration analytique des équations différentielles, même les plus simples, est énorme et assez confuse. Bien que, ironiquement, l'intégration des ODE à l'aide de méthodes numériques informatiques soit en fait relativement facile à comprendre. Ensuite, je décrirai un intégrateur numérique simple basé sur la méthode d'Euler, et le raffinerai dans le prochain article.

Presque tous les intégrateurs numériques, mais aucun autre aussi explicite que la méthode d'Euler, sont simplement basés sur l'ancienne définition de l'informatique via la première dérivée de l'inclinaison: dy / dx détermine la pente de y en fonction de x. Par exemple, si nous avons l'équation linéaire y = 5x, alors dy / dx = 5 signifie que la pente est une constante égale à 5 pour tout x, et, comme vous pouvez le supposer, il s'agit d'une ligne droite. Un exemple un peu plus difficile est la parabole y = x2. Dans ce cas, dy / dx = 2x, et c'est une fonction pour déterminer la nouvelle inclinaison pour chaque coordonnée x. J'ai représenté y = x2 dans la figure 2: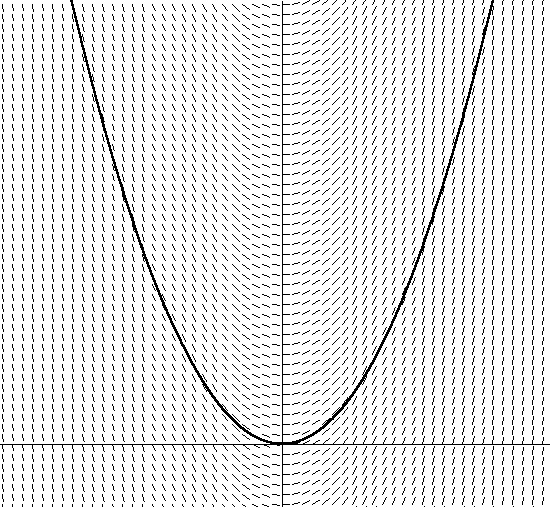



Figure 2. y = x2

En plus de cela, j'ai également hachuré la direction du vecteur oblique en résolvant l'équation dy / dx = 2x + C pour tout x. Faites attention au fait que l'angle du vecteur incliné est égal à la tangente de l'angle tangent en ce point. Notez également qu'il existe de nombreuses paraboles différentes qui satisfont l'angle de l'ensemble de tangentes, ne différant que par un décalage le long de l'axe y. Chacune de ces paraboles est obtenue en utilisant différentes constantes d'intégration, qui sont contenues dans l'équation dy / dx = 2x + C. La parabole que j'ai illustrée a une constante d'intégration de 0. Si je choisis une autre constante, par exemple 1, j'obtiens l'équation y = 2x + 1. Cela signifie qu'il existe une parabole similaire avec un décalage de 1 unité sur l'axe y.

Pensez maintenant au fait que si vous ne connaissez pas le champ de vecteurs de la figure 2 défini par une parabole, alors asseyez-vous simplement dans une flaque d'eau. Donc, si vous voulez résoudre l'équation tangente, il vous suffit de suivre la direction du vecteur à chaque point, en changeant de direction en fonction du changement de direction du champ de vecteur. Vous serez surpris de constater qu'après un certain temps, vous verrez que vous vous déplacez le long d'une trajectoire parabolique (ou le long d'une section de la parabole), selon l'endroit où vous avez commencé. Sans vous en rendre compte, vous avez intégré l'équation du champ vectoriel. Vous avez trouvé une parabole spécifique (en fonction de l'endroit où vous avez commencé ou des conditions initiales), en utilisant uniquement l'équation dérivée (calcul de dy / dx lorsque vous vous déplacez dans le champ vectoriel).

Faire de même pour une équation différentielle réelle est également simple. Pour une équation différentielle de type dy / dx = f (x, y), trouver la dérivée dy / dx comme tangente à f (x, y) décrit l'angle d'inclinaison de la tangente pour chaque coordonnée sur le graphique x, y. Si vous tracez un champ vectoriel donné par dy / dx = f (x, y), vous pouvez le suivre par analogie avec une parabole en trouvant la dérivée en chaque point et en suivant dans cette direction. La figure 2 montre le champ vectoriel de l'équation 12, notre équation de la résistance de l'air, avec la vitesse le long de l'axe vertical et le temps le long de l'horizontale (j'ai choisi arbitrairement m = 1 pour ce graphique).



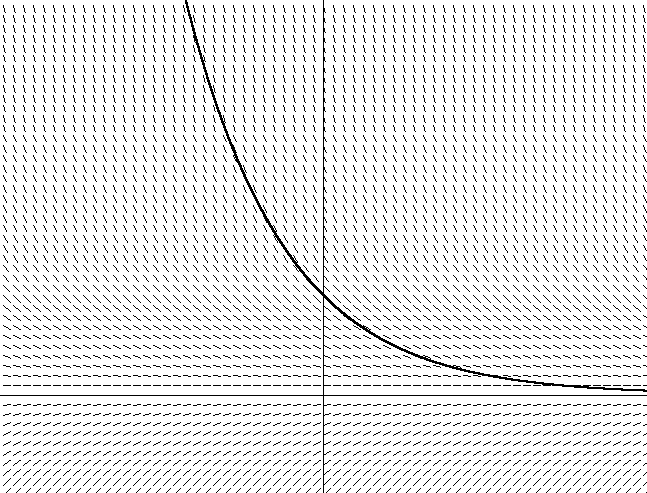Figure 3. dv / dt = -v / m

Il montre également l'une des nombreuses courbes possibles. Vous remarquerez peut-être que si vous choisissez la position initiale dans le graphique (qui dépend de la vitesse initiale dans l'équation), au fil du temps, la vitesse tendra vers zéro, car la force de friction ralentit le corps. Vous pouvez également voir comment la diminution de la vitesse dépend de la valeur actuelle de la vitesse - plus vous vous déplacez rapidement, plus elle diminue rapidement. Cela devient apparent lorsque la même chose découle de l'équation 12.

L'intégration numérique est similaire à ce que nous avons fait sur le graphique. L'algorithme d'Euler pour l'intégration numérique suit simplement le champ vectoriel conformément à la position initiale en trouvant la dérivée de l'équation (-v / m pour notre exemple avec la force de frottement) pour déterminer la pente au point courant, puis avance simplement pas à pas dans le temps, en fonction de valeur inchangée de h, le long de la pente. Ensuite, une nouvelle position est calculée pour déterminer la nouvelle pente après un certain intervalle de temps:

$$

$$y_{n+1} ≈ y_{ n } + {h(dy_{ n })\over dx}$$

Ou plus précisément pour notre équation de résistance à l'air:

$$

$$v_{ n+1 } ≈v_{ n }+{h( -v_{n})\over m}$$

De toute évidence, la méthode d'Euler donne une petite erreur à chaque pas de temps, car le vecteur de vitesse réelle (et donc la courbe de solution) se plie avec une déviation en chaque point, et l'algorithme d'Euler s'écarte légèrement de l'angle d'inclinaison. Mais si le pas de temps, h sont des quantités plutôt faibles, l'erreur tend vers zéro. Nous en discuterons plus en détail à l'avenir.

C'est tout ce que vous devez savoir sur l'intégration numérique à l'aide de la méthode Euler. Vous pouvez vous demander comment nous allons intégrer la vitesse pour obtenir les coordonnées. Nous utilisons simplement la méthode Euler à nouveau pour intégrer dr / dt = v, tout comme nous avons intégré dv / dt = a, par analogie. Nous obtenons deux équations différentielles connectées (une de plus de notre victoire):

$$

$$v_{n+1} ≈ v_n+hv'=v_n+{h F_n\over M }$$

$$

$$r_{ n+1 } = r_n + hr_n'= r_n+hv_n$$

Cela nous donne un algorithme alternatif pour calculer les coordonnées après l'action de toute force appliquée arbitrairement sur notre objet (qui peut dépendre de la vitesse, comme nous l'avons vu, ou du temps, ou même de la position de notre corps et d'autres corps, ou tout d'un coup!). Pour la méthode Euler, peu importe à quoi ressemble la force appliquée, car vous pouvez la calculer à tout moment. Euler s'intéresse à l'ampleur de l'effet de la force sur la masse, comme incliné, et c'est tout.
J'ai manqué d'espace, donc je n'ai aucun moyen de fournir des liens. La prochaine fois, je conseillerai divers livres merveilleux et nous découvrirons comment calculer la rotation des solides.

Et bien que son corps ne soit pas aussi solide que nous le souhaiterions, Chris Hecker a une personnalité dynamique. Si vous appliquez la force, il répondra par e-mail à checker@bix.com.

Notes du traducteur: un jeu de mots est présenté ici, le sujet de l'article et son contenu sont joués.

PS L'auteur de la traduction remercie tout particulièrement les utilisateurs de berez et MarazmDed pour leur révision de la traduction. Je vous remercie!