Collé par des dizaines de capteurs, «l'objet de recherche» lors de tests dynamiques à grande échelle (par exemple, lors de l'étude de l'activité vibratoire du véhicule) nous fournit facilement une grande quantité de données, mais il n'est souvent pas très clair de savoir quoi en faire. Il en va de même pour la modélisation par simulation de processus dynamiques de systèmes à grand nombre de degrés de liberté.
Cela peut ne pas être complètement clair pour ceux qui ne rencontrent pas régulièrement de problème, mais - en règle générale, regarder l'animation correspondante d'un processus stochastique dans le temps et l'espace est presque inutile. Où ça casse ou pourquoi ça tremble comme ça - généralement «non visible». Ce qu'ils ont trouvé en plus de l'animation, je vais vous le dire ci-dessous, mais je le recommanderai.
Au moyen d'une procédure élémentaire, on peut également obtenir les «formes» spatiales des oscillations elles-mêmes, d'ailleurs, ce sont précisément les manifestations réelles dans des conditions de chargement données et l'intensité de leur manifestation (dispersion; si désiré, les processus eux-mêmes).
Source
multicanal
le processus
 | Décomposition
|
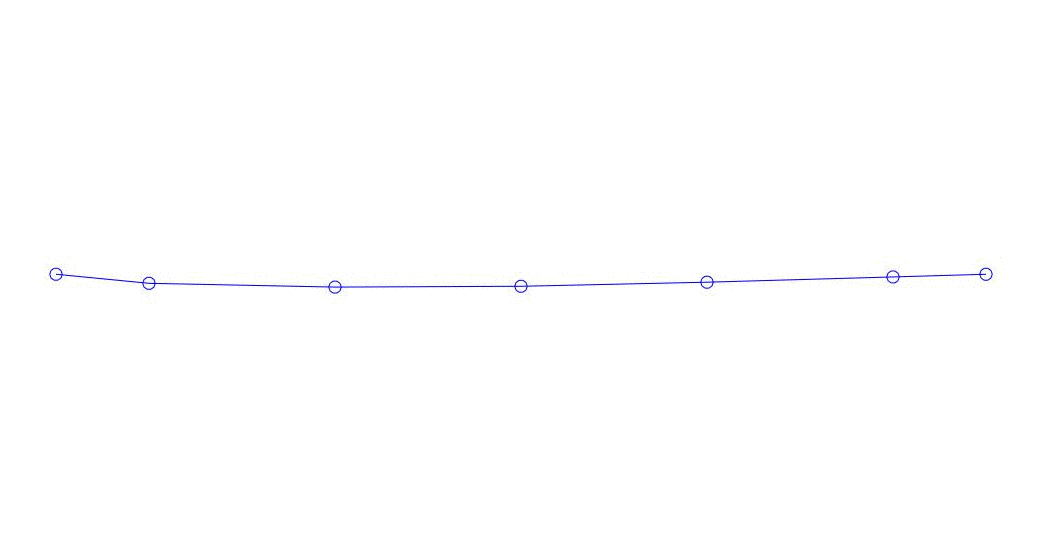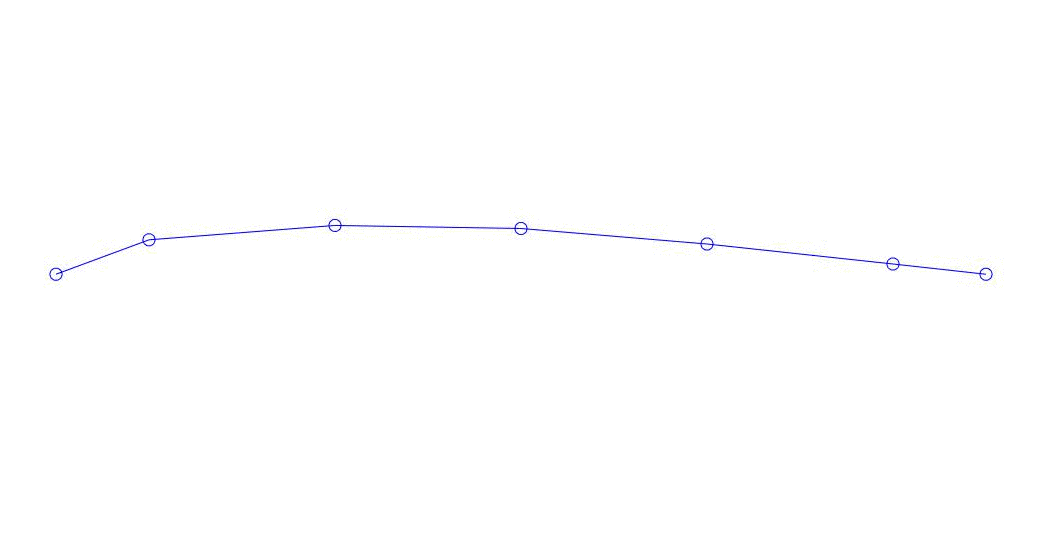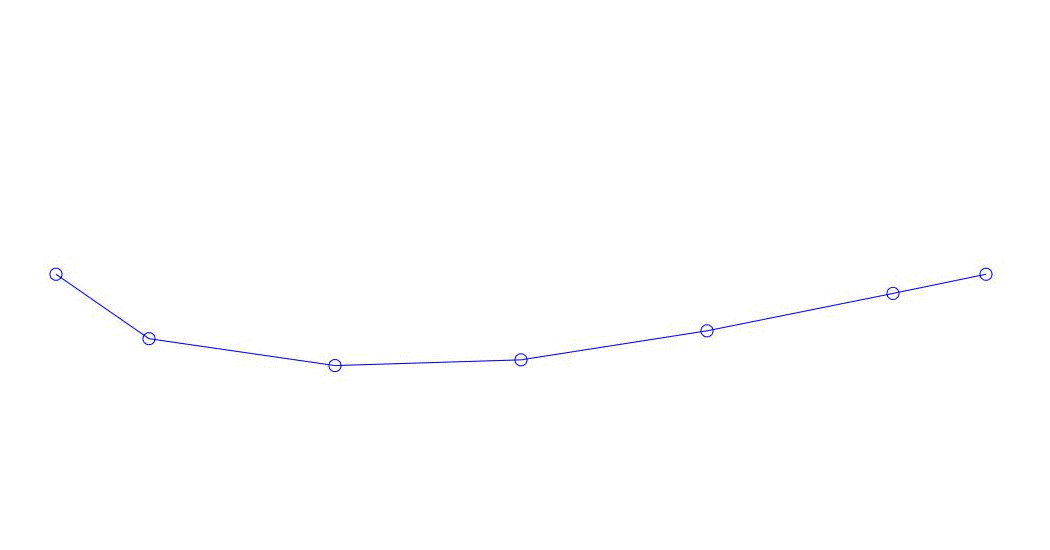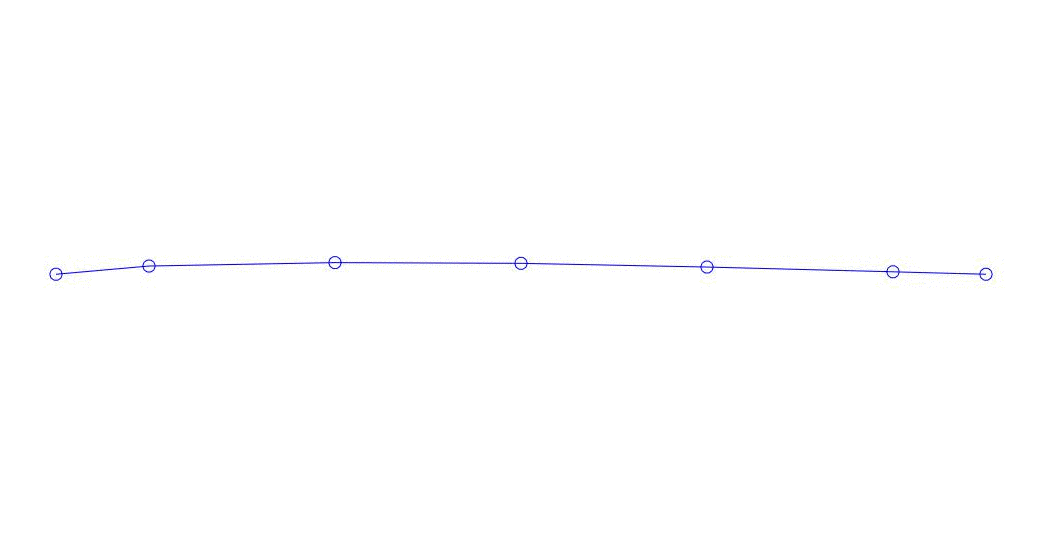
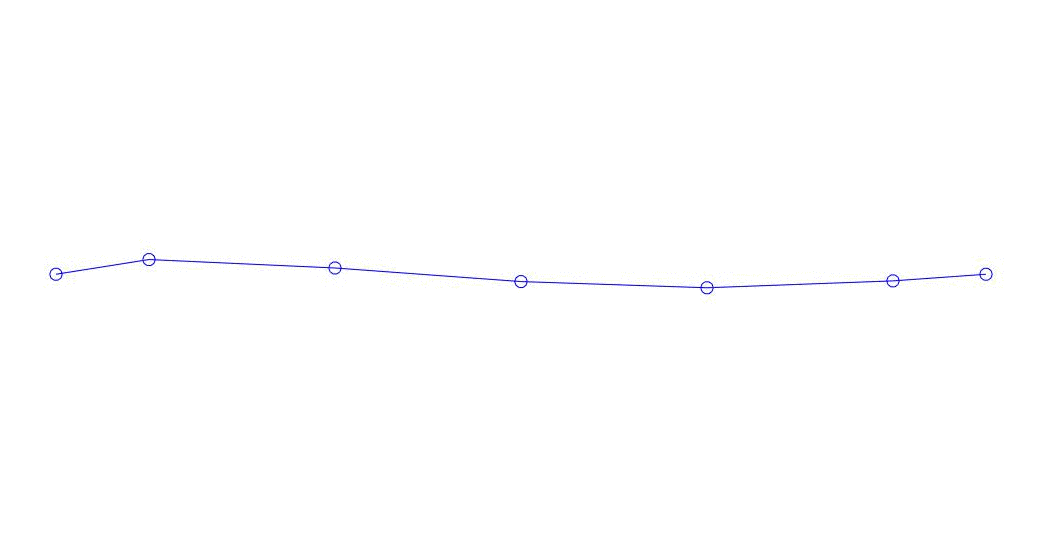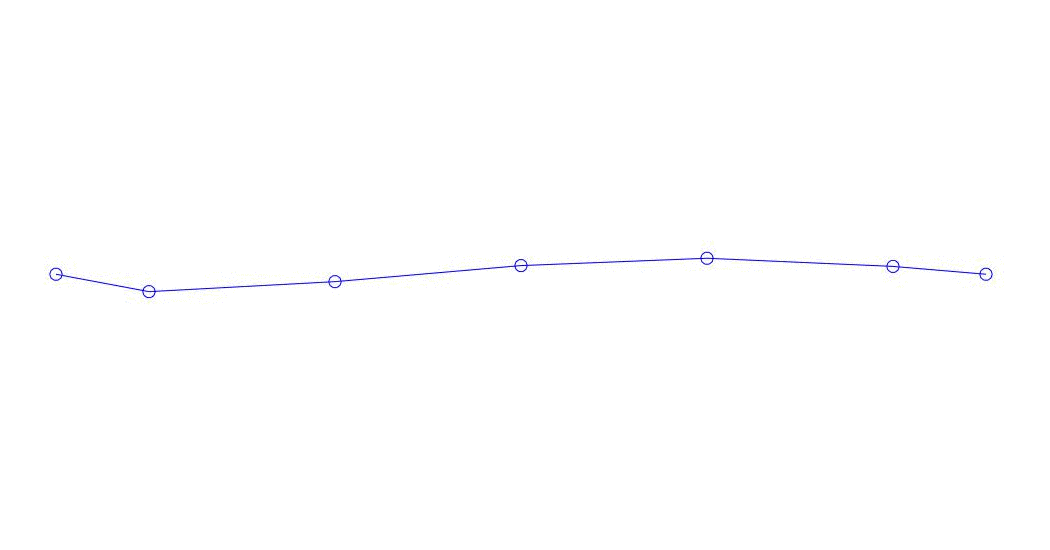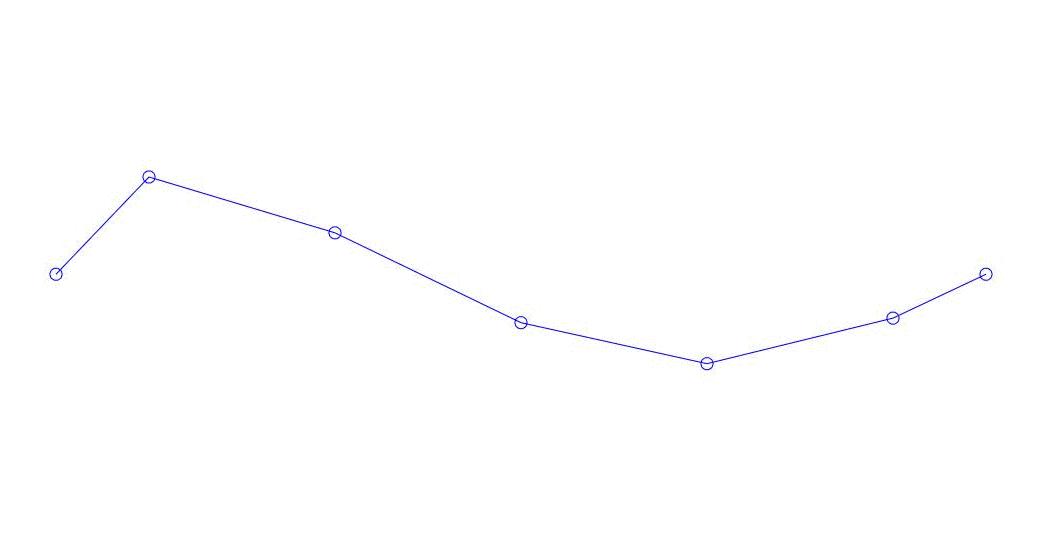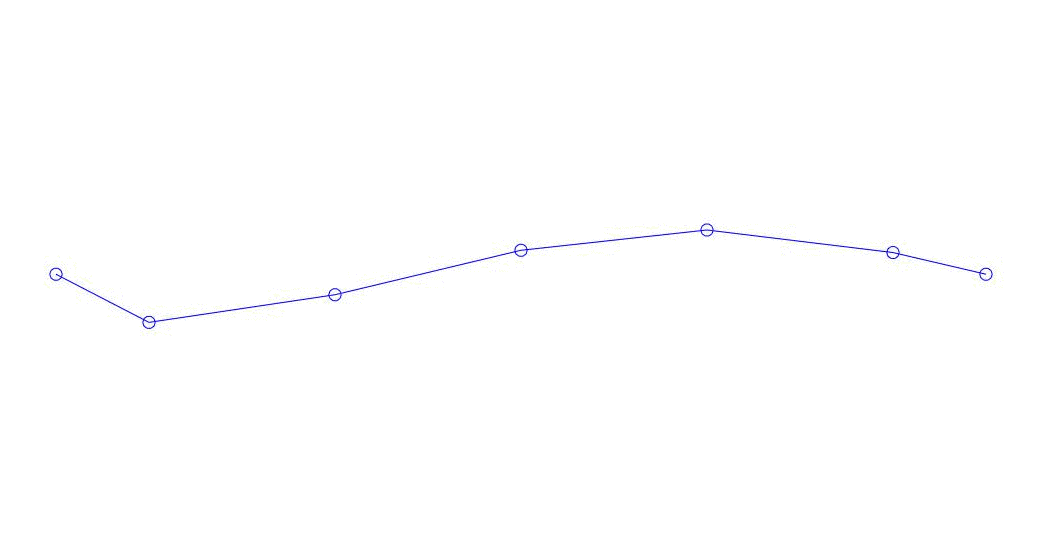
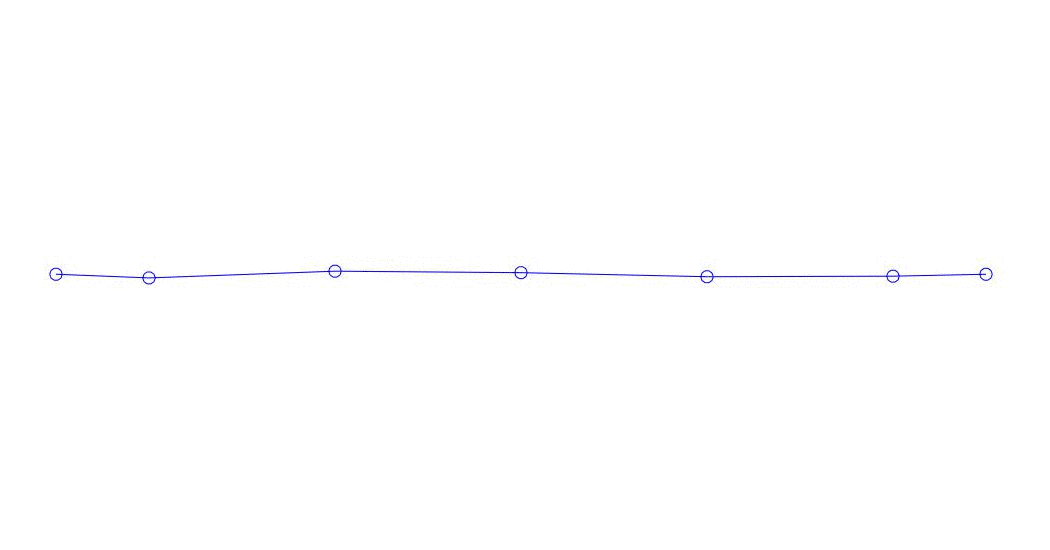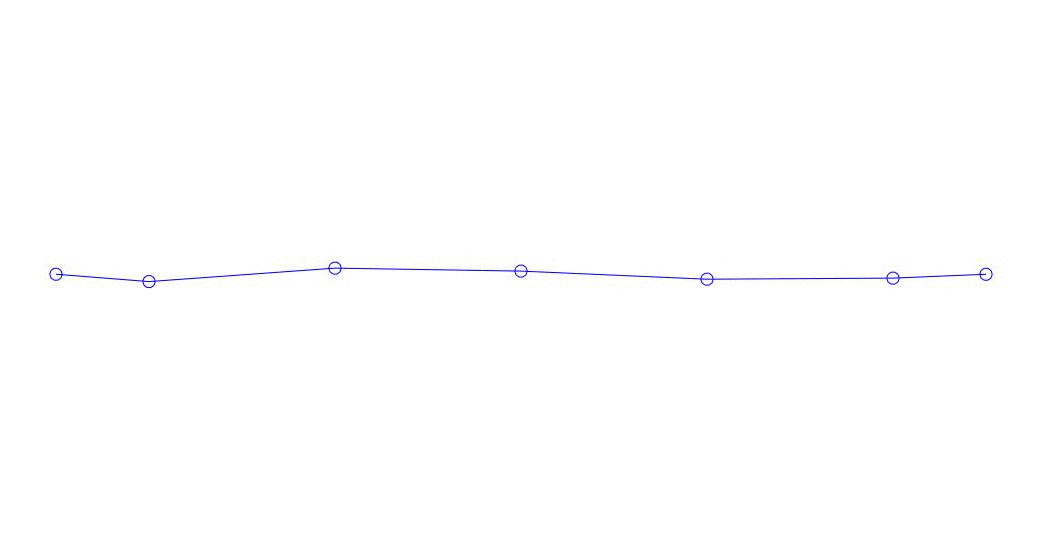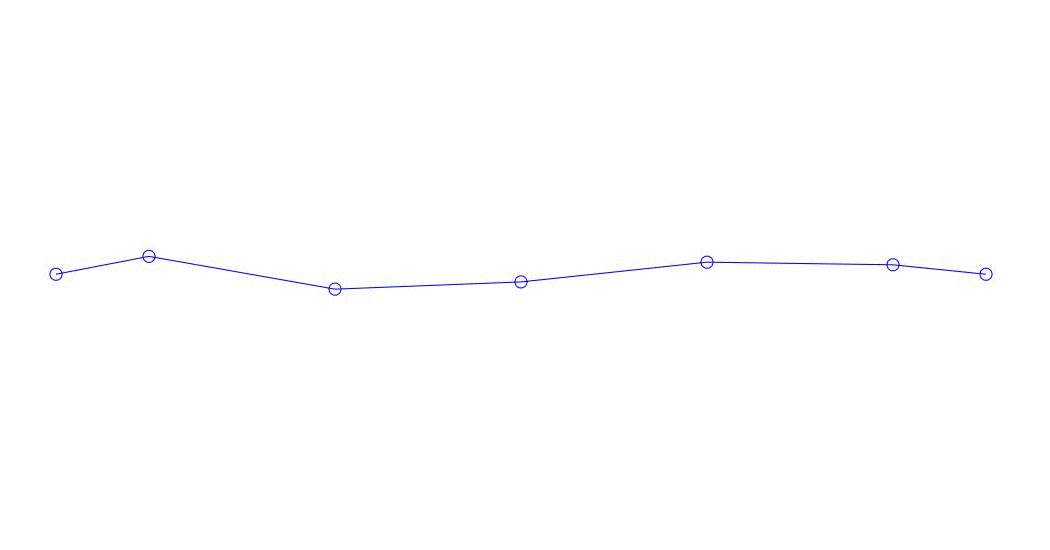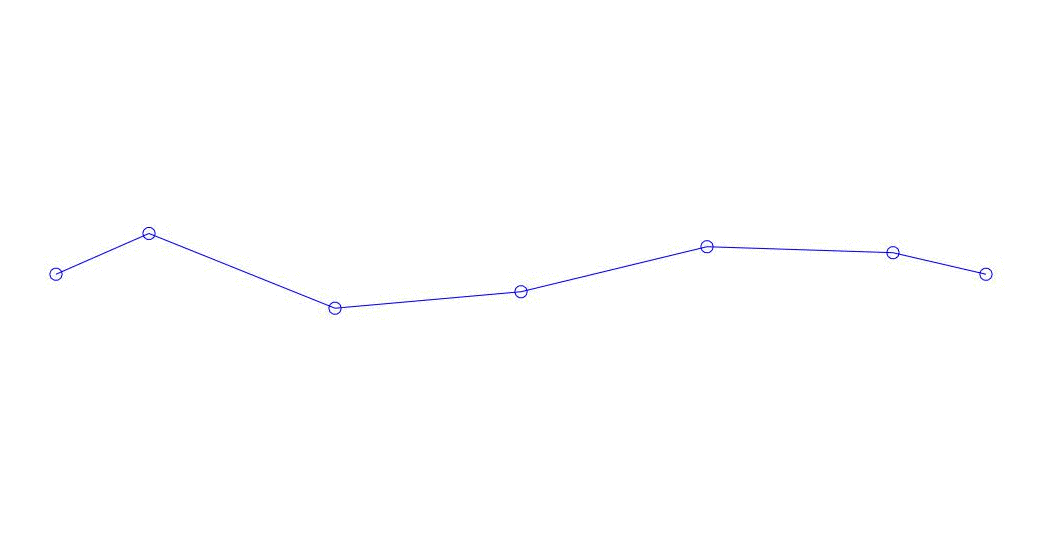
Fig. 1 Décomposition d'une réponse multicanal en pseudo-formes. "String dans un milieu visqueux" (voir figure 2)
En plus de l'animation, on sait que les études "par paires" (spectres mutuels, etc.) ne donnent bien sûr pas une image générale.
De telles méthodes sont assez évidentes - en «découpant» des bandes très étroites du spectre correspondant aux pics de résonance dans les spectrogrammes, les méthodes de spectrogramme (encore «par paires») produisent des quasi-formes de vibrations presque harmoniques (hautement corrélées).
En plus de la complexité technique évidente, l'inconvénient de ces méthodes est que vous devez généralement choisir "avec succès" un canal "de référence", ce qui n'est pas toujours possible. En conséquence, de très grandes erreurs se produisent dans les phases mutuelles des processus. En outre, la forme spatiale distincte des oscillations et sans ces erreurs, en raison des propriétés d'un système linéaire, peut se révéler «complexe» (non-phase), ce que sa valeur pour une analyse subjective ultérieure réduit généralement (pas toujours) de manière significative.
On connaît une étude à 4 canaux des vibrations de torsion (le système porteur d'un bus moyen), qui est allouée en un seul processus en utilisant la forme vibratoire spatiale déterminée par l'inspiration du chercheur - les lectures de deux capteurs situés en diagonale aux coins du corps ont été ajoutées (prises à partir de «+»), à partir de ils ont été soustraits (tirés de «-») le témoignage de deux autres personnes situées de façon symétrique.
Même avec un petit nombre de capteurs, cette approche peut ne pas être entièrement bonne. Par exemple, le châssis d'un camion est généralement beaucoup plus malléable dans la partie sous-moteur (avant), respectivement, une forme de torsion, peut-être devrait-il être supposé sous une forme plus complexe (probablement avec des coefficients «croissants» pour les capteurs avant - et en même temps, la question de la justification de l'acceptation acceptée modèles). Avec un plus grand nombre de canaux de surveillance, tout cela est très compliqué et mal justifié.
La séparation explicite (en processus séparés) de plusieurs modes de vibration (modes), préalablement déterminée à partir d'une autre expérience ou simulation, a été une fois proposée par moi (probablement, pas seulement par moi) et a été appelée par mon chef puis «la méthode de décomposition modale». Il était censé analyser les résultats des tests sur le terrain de cette manière et déterminer les vecteurs de leurs propres formes par des tests en banc (ou modélisation par éléments finis).
En fait, ils l'ont fait, mais en même temps, cela s'est avéré.
Il est clair que les «expérimentateurs de banc», contrairement aux «polygones», sont disponibles pour une observation synchrone, un véritable processus inquiétant. Cela leur a donné un grand avantage - ils pouvaient déterminer les véritables fonctions de transfert et utiliser le matériel et les logiciels disponibles pour déterminer expérimentalement leurs propres formes et fréquences de vibrations structurelles (sur la base du couvfitting, «couper» les plages de fréquences «à l'œil» et indiquer au système combien de formes il y a trouver; aussi plutôt art que science, mais quand même).
Cependant. Ils ont clairement évité d'explorer un objet tel qu'un assemblage de voiture, préférant les cadres individuels, les corps de support, etc. - objets à très faible amortissement. Il s'agit de tests modaux sur banc - la détermination des fréquences et des formes naturelles. Pas sur la simulation. Des modes de vibration intrinsèques plausibles sur des objets légèrement plus fortement amortis peuvent être expérimentalement obtenus expérimentalement, mais beaucoup plus difficiles.
Des informations très précieuses se sont avérées concerner ces «préférences». Si très, très brièvement, seules les conclusions qui ont été par la suite dégagées progressivement: s'efforcer de décomposer précisément la réponse sur les vraies formes propres de la construction ne valent guère la peine, malgré la «beauté» de l'idée.
Si c'est «sur vos doigts», alors la raison est probablement avec une forte probabilité, comme - selon la perturbation externe, les «modes de vibration naturels» (plus précisément, les processus «modaux» stationnaires correspondant aux modes de vibration naturels) seront très probablement comme ça ou sinon, ils sont corrélés entre eux, formant en fait d'autres formes spatiales de vibrations, à un degré ou un autre différent du leur, et cela se manifeste naturellement dans une forte dépendance à l'amortissement de la structure.
Pour une brève explication «du contraire» - deux harmoniques «non amorties» différentes ne sont naturellement pas corrélées, toujours rien. (Explication. L'effet susmentionné du «mélange de formes propres» est observé à la fois en l'absence de «non-linéarités significatives» et en dehors des «formes complexes» avec un amortissement «disproportionné» dans les systèmes linéaires.)
Sur la base de ce qui précède, il est proposé de présenter la réponse du système comme la somme de plusieurs processus indépendants de la corrélation tels que certaines formes de vibration (flexion, torsion, etc.). Une telle analyse est très simple, en règle générale, elle donne des résultats très précieux. Les formes obtenues peuvent être similaires aux modes propres d'oscillation du système, ou non, mais elles reflètent toujours le comportement du système précisément dans des conditions d'influence extérieure réelle. de plus, ils reflètent le plus simple et le plus informatif possible, et leur séquence, classée par leurs variances, est une série approximative.
Pour obtenir la décomposition qui nous intéresse, nous considérons (1),
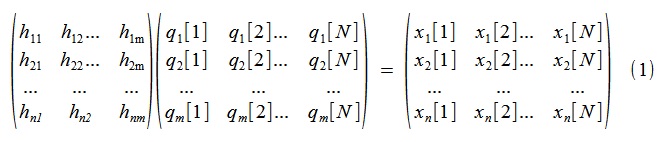
ou, de la même manière, de manière compacte, (2),
où
x est la réponse physique à n canaux du système avec la durée de N échantillons directement obtenus dans l'expérience,
q est le véritable processus «modal» à canaux m avec des canaux mutuellement non corrélés, H est la matrice de colonnes décrivant les modes de vibration en phase («réels») souhaités.
De manière générale, m <n est par la suite attendu (le nombre de formes est inférieur au nombre de canaux de réponse physique), mais au départ on suppose m = n, puis si H et
q sont de rang n, (2) en tout cas, est satisfait sans résidu, on arrive évidemment à
| H · Rqq [0] · H T = Rxx [0] (3) |
ou plus en détail
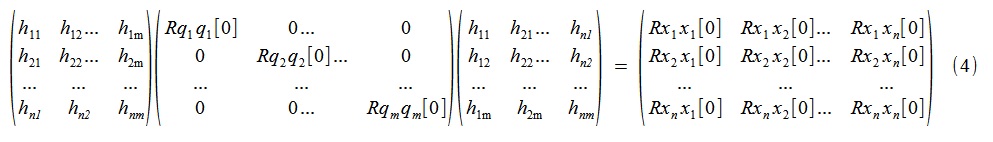
C'est-à-dire que la recherche des modes de vibration «pseudo-appropriés» recherchés et des processus correspondants non corrélés (avec un décalage nul)
q se réduit à la décomposition spectrale (en termes de vecteurs propres et de nombres) de la matrice symétrique Rxx [0] (composée des valeurs des corrélations automatiques et croisées des processus
x pour lag Δτ = 0) Ses propres vecteurs orthonormés nous donnent les formes souhaitées, et les valeurs propres réelles donnent les variances des processus correspondants (en plus des processus significatifs, il y aura très probablement des variances de ~ 0, donc en pratique généralement m <n). Si vous le souhaitez, vous pouvez toujours construire les processus eux-mêmes sous forme de réalisations temporaires, trouver leurs spectres, etc.
Pour clarifier ce qui précède, nous considérons un modèle d'un système mécanique linéaire à cinq degrés de liberté, simulant approximativement le comportement d'une corde dans un milieu visqueux (Fig.2),
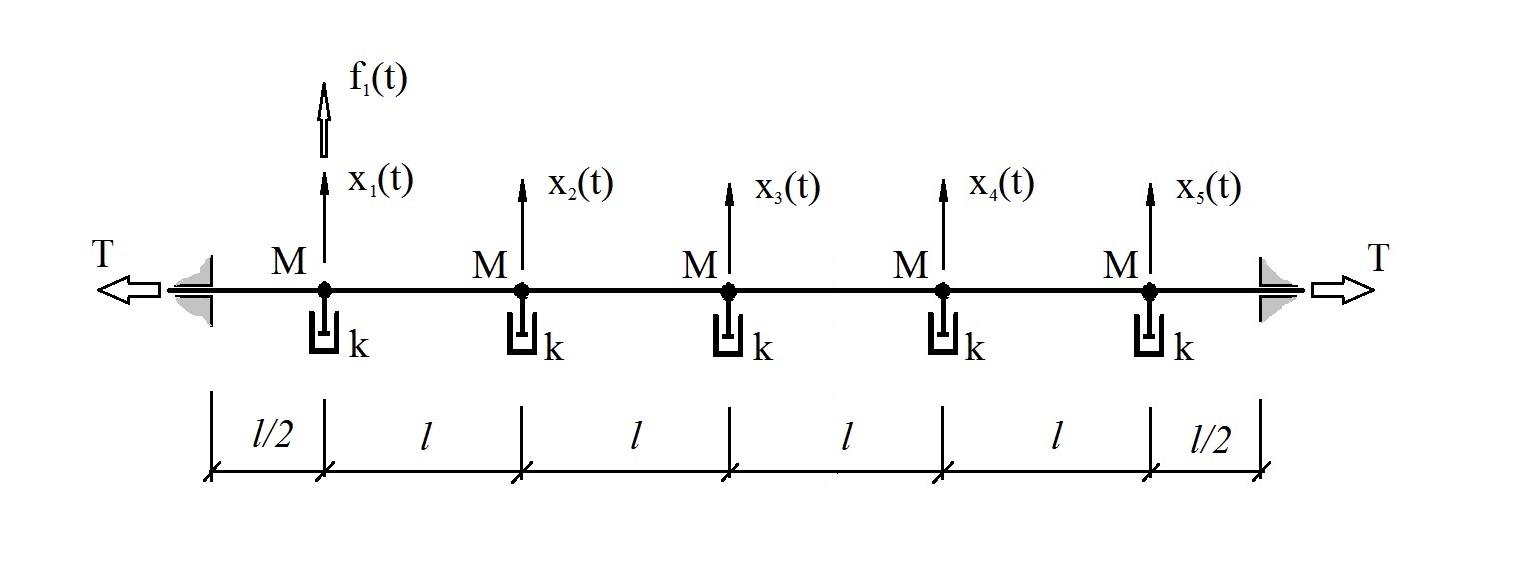Fig.2 Système de test.oscillant sous l'influence de la perturbation stochastique f
1 [i] du type de bruit rose (Fig. 3), intervalle d'échantillonnage Δt = 0,01 s, longueur de mise en œuvre 25000 échantillons (ci-après, les estimations de PSD sont obtenues par la méthode Welch, longueur de segment 1024, la fenêtre de Hamming est appliquée et 60% de chevauchement des segments.)
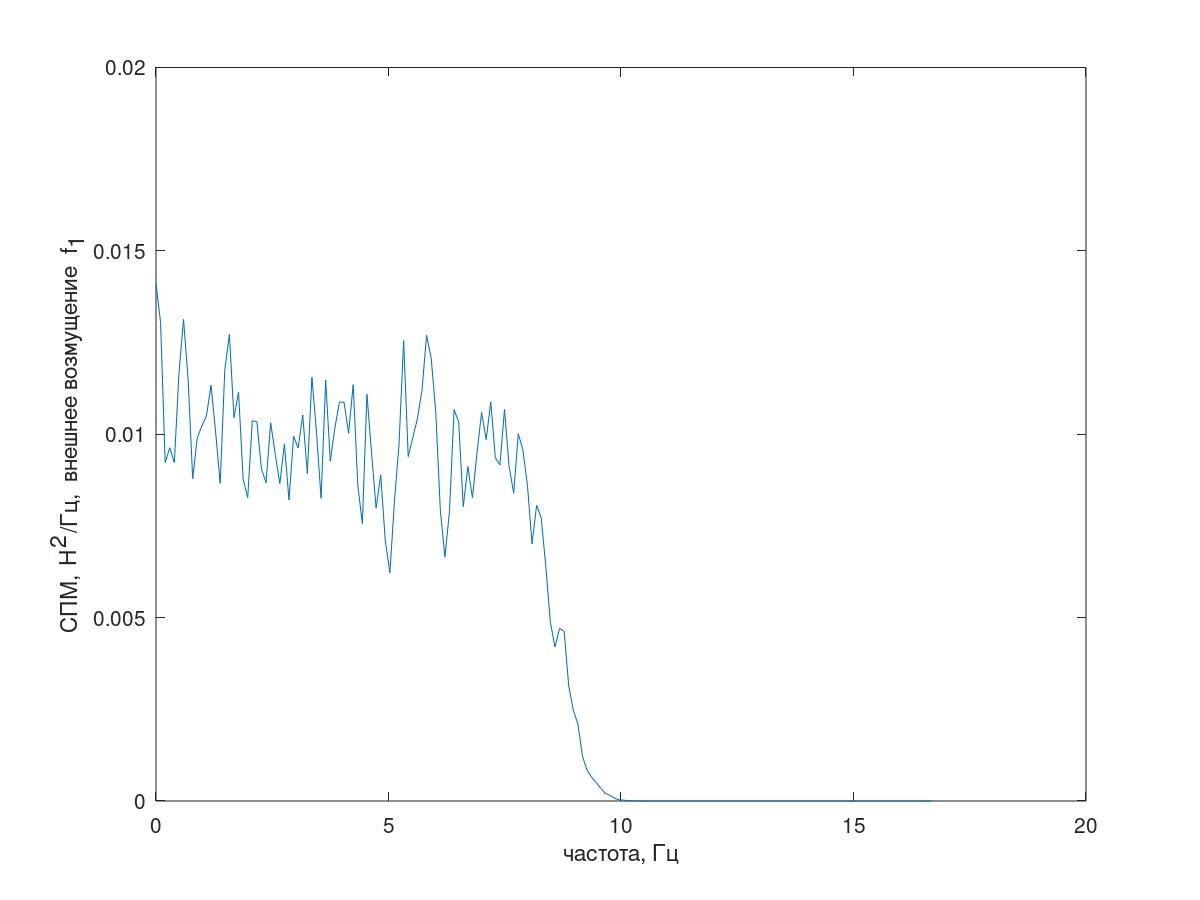Fig. 3 Spectre de perturbations externes.
Un fragment de la mise en œuvre temporaire de la perturbation est illustré à la figure 4.
Fig.4 Un fragment de la mise en œuvre temporaire de la perturbation entrante
En temps continu, le modèle est un système d'équations de diffusion (6),
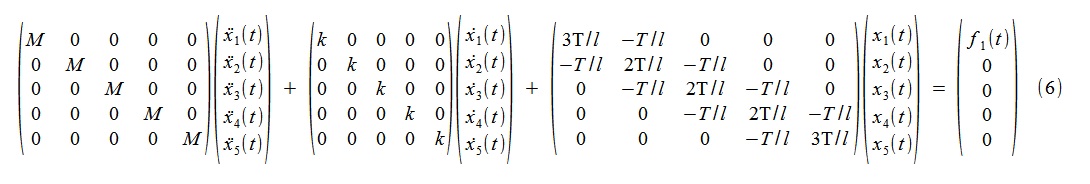
où M = 1 kg, k = 10 kg / s, T = 2000 N, l = 1 m.
Les matrices correspondantes (il est clair lesquelles) sont numériquement égales aux suivantes:
L'une des réponses en fréquence du système est représentée sur la figure 5.
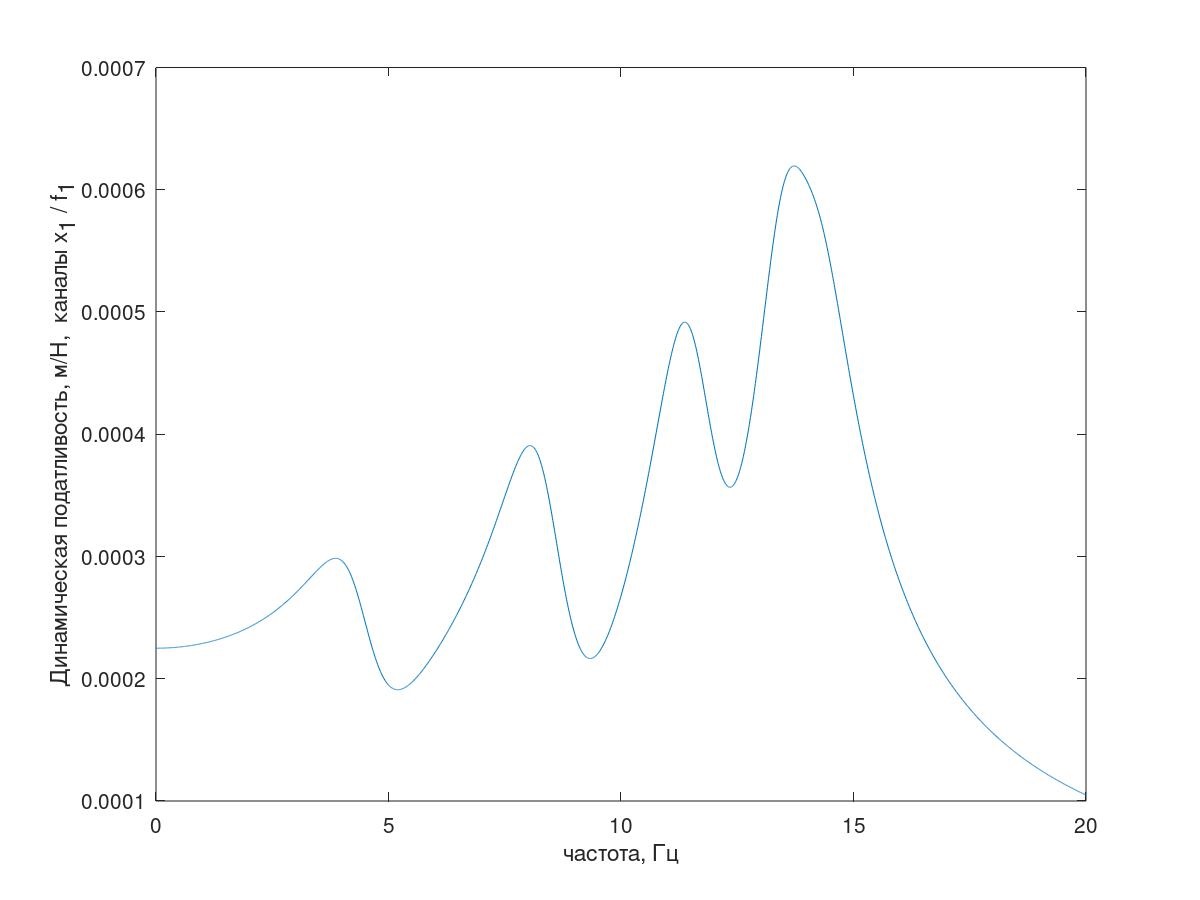Fig.5. Réponse en fréquence du système de test(Explication - tout est en ordre avec le nombre de pics de résonance, comme une explication de cette réponse en fréquence du système avec un amortissement conditionnellement réduit (k = 1 kg / s) est montrée dans la Fig.5)
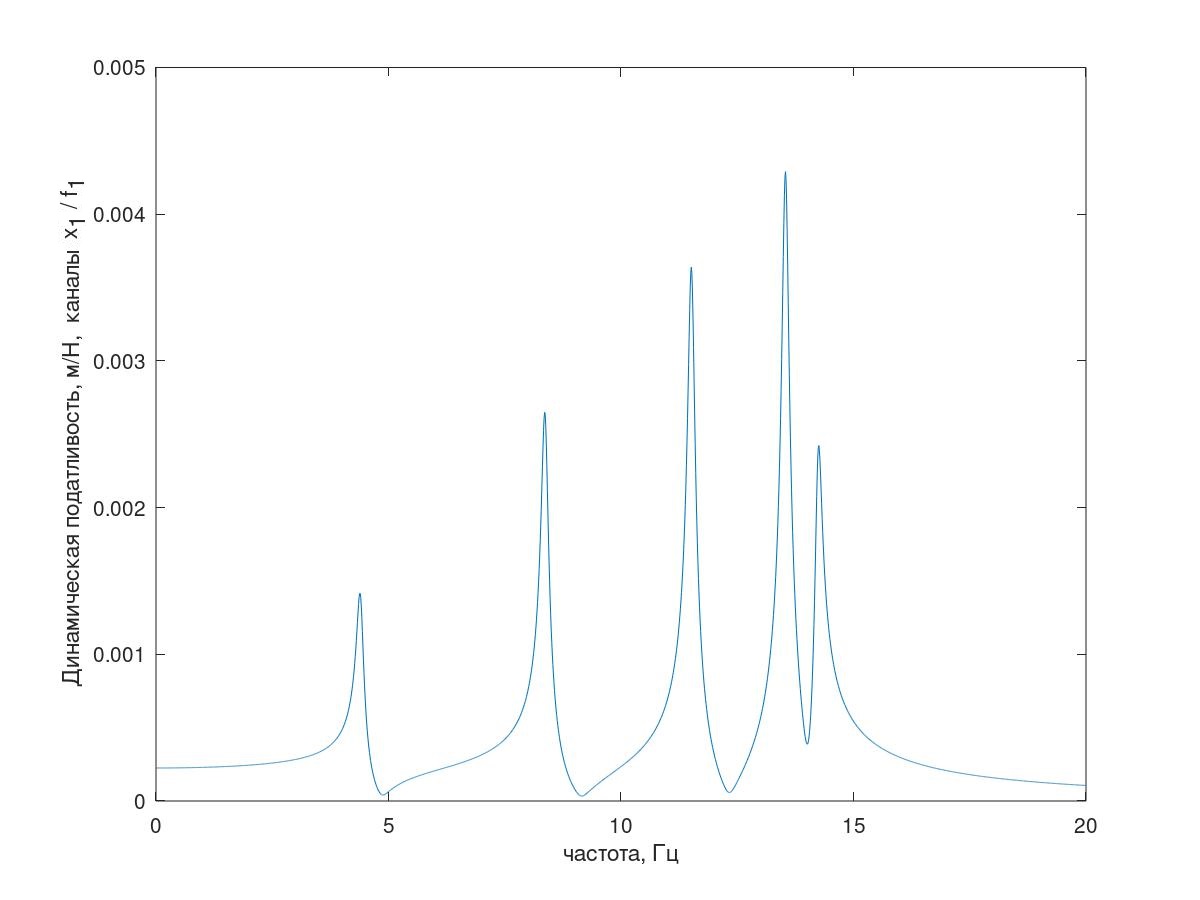Fig. 6 Explication pour cinq résonances.
Pour la simulation en temps discret, un modèle à différences finies est utilisé (les modèles Raman fonctionnent bien à de petits intervalles d'échantillonnage, comme cela a
été montré ).
Une petite digression. Quelque temps plus tard, dans le cadre d'un autre travail, une modélisation par différence finie de ce système de test par d'autres moyens a été réalisée (Xcos \ Simulink). Mathématiquement, les modèles sont identiques. Des images animées de la réponse du système à une seule impulsion au nœud n ° 1 et au nœud n ° 3 ont été obtenues. Les résultats sont ici intéressants du point de vue de la vérification du modèle de différence finie.
(La mise en mémoire tampon "imprévisible" des cadres logiciels libres gâche quelque peu les images, en particulier la seconde, mais, en principe, le résultat est très bon.)
Mais revenons à notre modèle Matlab (GNUOctave). Le spectre de réponse résultant est illustré sur la figure 7.
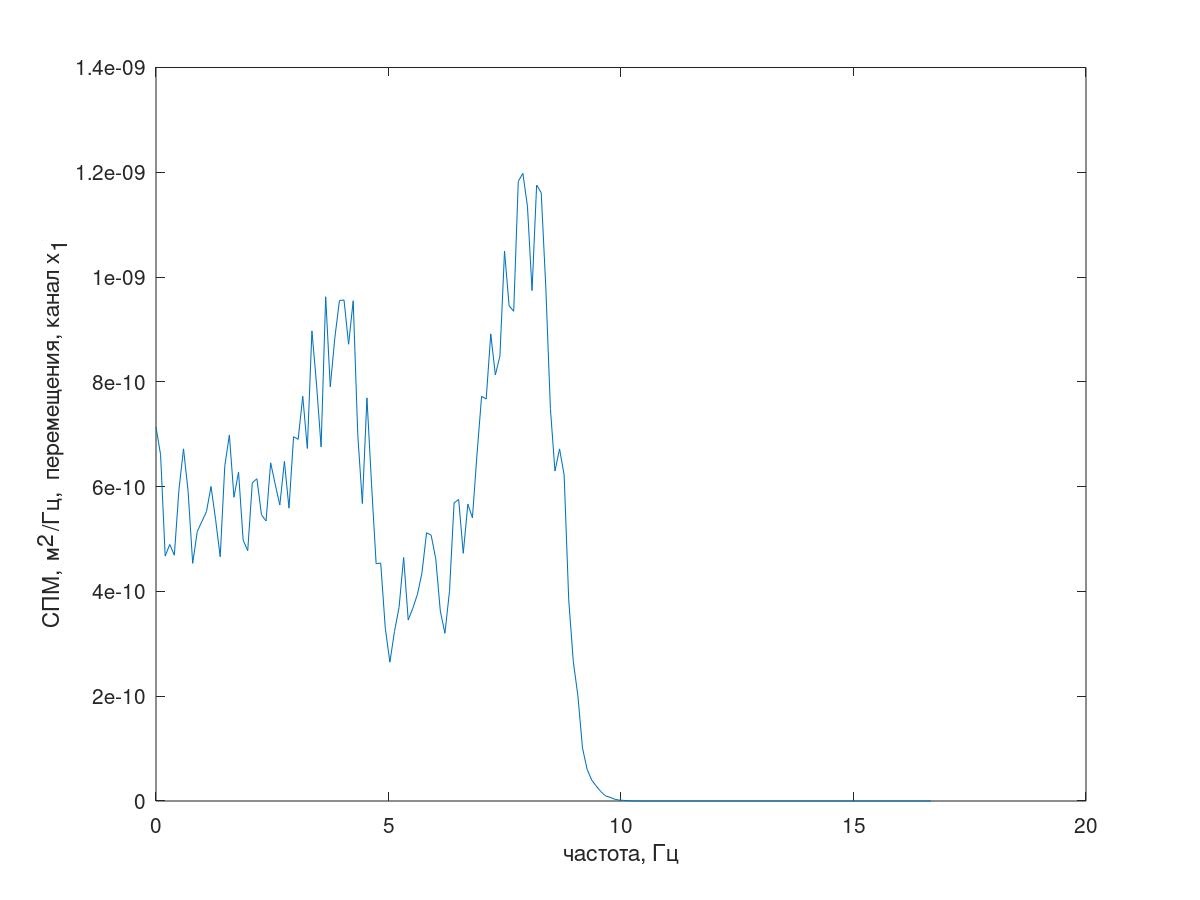Fig.7 Spectre de réponse (canal x 1 )De plus, la méthode de corrélation a été utilisée pour trouver les valeurs des corrélations automatiques et croisées des canaux de réponse.
Les résultats de l'application de la méthode en discussion: les variances des processus pseudo-modaux Rqq et les formes pseudo-distinctes de H elles-mêmes ont été trouvées:
Les trois premiers processus de décomposition, l'animation de l'ensemble du processus multicanal et les trois premiers modes de vibration correspondants dans 32 échantillons (de 6714 à 6746 décomptes, soit de 67,13 s en termes de magnitude) sont apparemment quantitativement significatifs (par les valeurs de leurs dispersions en Rqq) 67,63 s heure actuelle) est illustré à la Fig. 1 au début de l'article. Comme vous pouvez le voir, ces pseudo-formes ont des similitudes avec leurs propres formes de vibrations des cordes.
L'expérience accumulée indique les caractéristiques suivantes de cette méthode.
- La méthode est sensible au bruit extérieur, y compris haute fréquence. Il existe un danger d'obtenir des résultats «aléatoires» (avec une grande erreur aléatoire) et l'irréproductibilité apparente des résultats expérimentaux. Il est nécessaire de filtrer soigneusement la partie non fonctionnelle (quantitativement insignifiante) de la gamme de fréquences du signal multicanal. (À un moment donné, les travaux dans ce sens ont même été arrêtés en raison de rapports d'expérimentateurs sur «l'absence» de corrélation entre les canaux - l'effet d'un fort bruit)
- Les meilleurs résultats ont été obtenus avec un nombre de canaux d'observation significativement supérieur au nombre de manifestations attendues de formes vibratoires (nombre de pics résonants dans la gamme étudiée), c'est-à-dire pour m << n.
- Avec des facteurs Q élevés, les systèmes de pseudo-formes semblent tendre vers les véritables modes intrinsèques du système. Les résultats obtenus sur de tels systèmes sont plus stables en cas de bruit.
- Si la paire de valeurs propres Rxx [0] coïncide ou même converge, la paire des pseudo-formes correspondantes est apparemment déterminée jusqu'à leurs combinaisons linéaires indépendantes - ces formes ne peuvent pas être séparées entre elles dans des conditions expérimentales données.
- Apparemment, en comparant les vraies formes (trouvées par d'autres méthodes) et les pseudo-formes considérées, avec une certaine probabilité, il est possible de trouver les points d'application de la perturbation externe (en particulier avec une perturbation à petit canal), si un tel problème est pertinent.