Présentation
Le mot anglais wavelet (du français "ondelette") se traduit littéralement par "courte (petite) onde". Dans diverses traductions d'articles étrangers en russe, il y a aussi des termes: "rafale", "fonction de rafale", "fonction de basse onde", "vague", etc.
La transformée en ondelettes (VP) est largement utilisée pour l'analyse du signal. De plus, il trouve une grande application dans le domaine de la compression de données. Le VP d'un signal unidimensionnel est sa représentation sous la forme d'une série généralisée ou intégrale de Fourier sur un système de fonctions de base.
psiab(t)= frac1 sqrta psi left( fract−ba right) , (1)
construit à partir de l'ondelette mère (source)
psi(t) possédant certaines propriétés dues aux opérations de décalage temporel (b) et aux changements d'échelle temporelle (a).
Multiplicateur
1/ sqrta assure l'indépendance de la norme des fonctions (1) par rapport au nombre de mise à l'échelle (a). Pour les valeurs données des paramètres a et b, la fonction
psiab(t) et il y a une ondelette générée par l'ondelette mère
psi(t) .
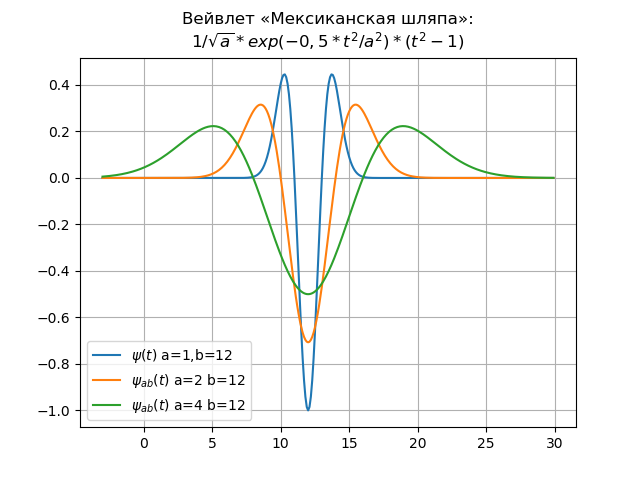
Un exemple est l'ondelette mexicaine dans les domaines temporel et fréquentiel:
Liste d'ondelettes pour le domaine temporelfrom numpy import* import matplotlib.pyplot as plt x= arange(-4,30,0.01) def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f plt.title(" « »:\n$1/\sqrt{a}*exp(-0,5*t^{2}/a^{2})*(t^{2}-1)$") y=[w(1,12,t) for t in x] plt.plot(x,y,label="$\psi(t)$ a=1,b=12") y=[w(2,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=2 b=12") y=[w(4,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=4 b=12") plt.legend(loc='best') plt.grid(True) plt.show()
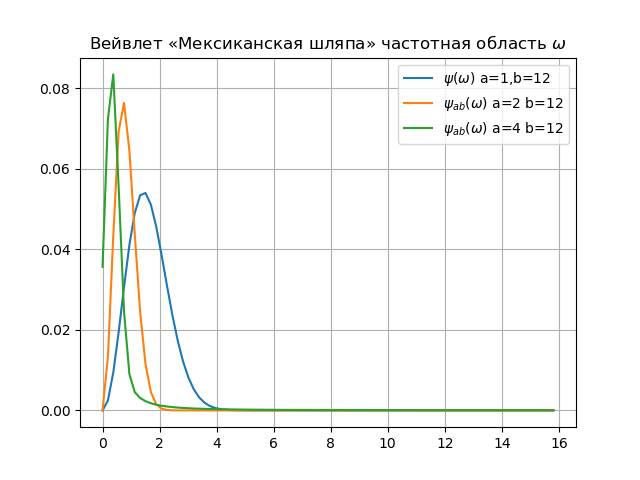
Liste pour le spectre d'ondelettes from numpy import* from pylab import * from scipy import * import os def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f x= arange(-4,30,0.2) def plotSpectrum(y,Fs): n = len(y) k = arange(n) T = n/Fs frq = k/T frq = frq[range(int(n/2))] Y = fft(y)/n Y = Y[range(int(n/2))] return Y,frq xlabel('f (Hz)') ylabel('|Y(f)|') Fs=1024.0 y=[w(1,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi(\omega)$ a=1,b=12") y=[w(2,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=2 b=12") y=[w(4,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=4 b=12") plt.title(" « » $\omega$") legend(loc='best') grid(True) show()
 Conclusion:
Conclusion:1. Entre le concept des harmoniques de Fourier et l'échelle de l'ondelette, il y a vraiment une relation. L'essentiel de cette relation est la proportion inverse de la fréquence et de l'échelle naturelles. De plus, en réduisant l'échelle, nous augmentons la bande passante du spectre d'ondelettes.
2. En changeant l'échelle (l'augmentation de a entraîne un rétrécissement du spectre de Fourier de la fonction
psiab(t) ), les ondelettes sont capables de détecter la différence de caractéristiques à différentes échelles (fréquences) et, en raison du décalage, d'analyser les propriétés du signal à différents points sur l'ensemble de l'intervalle étudié. Par conséquent, lors de l'analyse de signaux non stationnaires, en raison de la propriété de localité des ondelettes, ils obtiennent un avantage significatif sur la transformée de Fourier, qui ne donne que des informations globales sur les fréquences (échelles) du signal analysé, car le système de fonctions utilisé (exposant complexe ou sinus et cosinus) est défini sur intervalle infini.
3. Les listes ci-dessus écrites dans le langage Python de haut niveau librement distribué vous permettent de sélectionner des fonctions pour les ondelettes qui répondent aux exigences spécifiées. Cependant, il est en outre nécessaire de prendre en compte tous les principaux signes d'ondelettes.
Les principaux signes de l'ondelette
Limité. Le carré de la norme de la fonction doit être fini:
gauche | psi right |2= int infty− infty left| psi(t) right|2dt< infty . (2)
Localisation VP, contrairement à la transformée de Fourier, utilise une fonction initiale localisée à la fois en temps et en fréquence. Pour ce faire, il suffit que les conditions suivantes soient remplies:
gauche| psi(t) right| leqC(1+ left|t right|)−1− varepsilon et
gauche|S psi( omega) right| leqC(1+ left| omega right|)−1− varepsilon à
varepsilon>0 , (3)
Par exemple, une fonction delta
delta(t) et la fonction harmonique ne remplissent pas la condition nécessaire pour une localisation simultanée dans les domaines temporel et fréquentiel.
Zéro moyenne. Le graphique de la fonction d'origine doit osciller (être alterné) autour de zéro sur l'axe du temps et avoir une zone nulle:
int infty− infty psi(t)dt=0 . (4)
De cette condition, il devient clair le choix du nom "ondelette" - une petite vague.
Zone de fonction égale à zéro
psi(t) , c'est-à-dire moment zéro, conduit au fait que la transformée de Fourier
S psi( omega) cette fonction est égale à zéro pour
omega=0 et a la forme d'un filtre passe-bande. Pour diverses valeurs (a), ce sera un ensemble de filtres passe-bande.
Souvent, pour les applications, il est nécessaire que non seulement zéro, mais tous les n premiers moments soient égaux à zéro:
int infty− inftytn psi(t)dt=0 . (5)
Les n-èmes ondelettes permettent d'analyser la structure plus fine (haute fréquence) du signal, en supprimant ses composantes qui changent lentement.
Self-made. Une caractéristique de VP est son auto-similitude. Toutes les ondelettes d'une famille spécifique
psiab(t) avoir le même nombre d'oscillations que l'ondelette mère
psi(t) , car obtenu à partir de celui-ci au moyen de transformations d'échelle (a) et de décalage (b).
Transformation en ondelettes continue
Transformée en ondelettes continue (intégrale) (NVP ou WT - transformée en ondelettes continue). Nous construisons la base
psiab(t) utilisant des transformations d'échelle continues (a) et des transferts (b) de l'ondelette mère
psi(t) avec des valeurs arbitraires des paramètres de base a et b dans la formule (1).
Ensuite, par définition, la NVP directe (analyse) et inverse (synthèse) (c'est-à-dire PNVP et ONVP) du signal S (t) s'écrit comme suit:
Ws(a,b)=(S(t), psiab(t))= frac1 sqrta int infty− inftyS(t) psi left( fractba right)dt , (6)
S(t)= frac1C psi int infty− infty int infty− inftyWs(a,b) psiab(t) fracdadba2 , (7)
où
C psi - coefficient de normalisation,
C psi= int infty− infty left| psi( omega) droite|2 gauche| omega right|−1d omega< inftyoù: (•, •) est le produit scalaire des facteurs correspondants,
mathbf psi( omega) - Transformée de Fourier d'une ondelette
psi(t) . Pour ondelettes orthonormales
C psi=1 .
Il résulte de (6) que le spectre des ondelettes
Ws(b,a) (spectre d'ondelettes, ou spectre d'échelle de temps), contrairement au spectre de Fourier (spectre unique), est fonction de deux arguments: le premier argument a (échelle de temps) est similaire à la période d'oscillation, c'est-à-dire est inverse de la fréquence et le second b –– est similaire au décalage du signal le long de l'axe du temps.
Il convient de noter que
Ws(b,a0) caractérise la dépendance temporelle (à
a=a0) , tandis que les dépendances
Ws(a,b0) il est possible de faire correspondre la dépendance en fréquence (pour
b=b0 )
Si le signal étudié S (t) est une seule impulsion de durée
tauu concentré dans le quartier
t=t0 , alors son spectre d'ondelettes aura la plus grande valeur au voisinage du point avec les coordonnées
a= tauu,b=t0 .
Méthodes de présentation Ws(b,a) peut être différent. Spectre
Ws(b,a) est une surface dans un espace tridimensionnel. Cependant, souvent au lieu de l'image de la surface, sa projection sur le plan ab est présentée avec des niveaux iso (ou des figures de différentes couleurs), qui permettent de suivre l'évolution de l'intensité des amplitudes EP à différentes échelles (a) et dans le temps (b).
De plus, ils représentent des lignes d'extrêmes locaux de ces surfaces, le soi-disant squelette (squelette), qui révèle la structure du signal analysé.
Transformation en ondelettes continue lors de la détermination du spectre d'ondelettes sur la base de l'ondelette mère - «chapeau mexicain».
D'autres ondelettes maternelles utilisées pour la NVP sont également utilisées:

VP continu est largement utilisé dans le traitement du signal. En particulier, l'analyse en ondelettes (VA) offre des opportunités uniques de reconnaître les caractéristiques locales et «subtiles» des signaux (fonctions), ce qui est important dans de nombreux domaines de l'ingénierie radio, des communications, de la radioélectronique, de la géophysique et d'autres branches de la science et de la technologie. Examinons cette possibilité avec quelques exemples simples.
Oscillation harmonique.Le signal a la forme:
s(t)=Asin( omegat− phi)où:
A=1V, omega= frac2 piT= frac2 pi50, psi=0Fonction de formation d'ondelettes:
MHAT(t):= fracd2dt2exp(−t2/2) ,
Ondelettes:
psi(a,b,t)= frac1 sqrtaMHAT left( fract−ba right) ,
Spectre d'ondelettes: N: = 256, a: = 1..30, b: = 0..50,
W(a,b):= intN−N psi(a,b,t)s(t)dt,Nab:=W(a,b). .
Liste des programmes from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 T=50 def S(t): return sin(2*pi*t/T) plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,100,1)] x=[t for t in arange(0,100,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49,49) fig = plt.figure("- : ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z,100) plt.show()
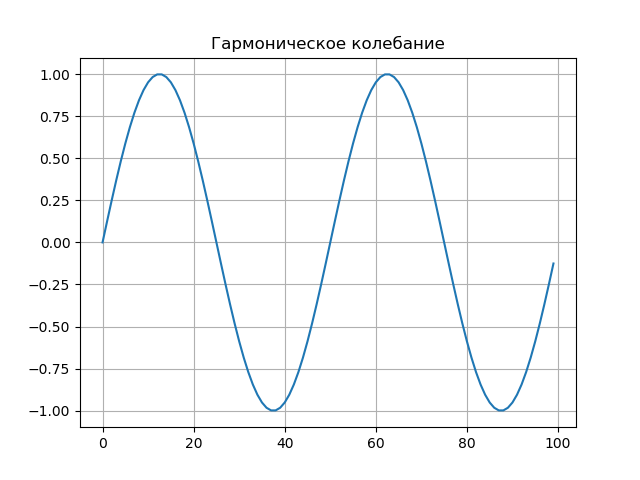
Graphique du signal.

Graphique d'un spectre à deux paramètres
Nab=W(ab) affiché comme une surface dans un espace tridimensionnel.

Il convient de noter que la section W (a, b) pour l'échelle de temps
a=a0 caractérise l'oscillation initiale s (t). De plus, son amplitude est maximale à
a0:1/ omega . Dépendances
W(a0,b0) peut correspondre au spectre actuel des oscillations à
b=b0 .
La somme de deux oscillations harmoniques.Le signal a la forme:
s(t):=A1sin( omega1t)+A2sin( omega2t)où:
A1=A2=1V, omega1= frac2 piT1, omega2= frac2 piT2,T1=50s,T2=10s .
MHAT(t):= fracd2dt2 left[e−t2/2 right] , N: = 256,
psi(a,b,t):=MHAT left( fractba right),W(a,b):= intN−N psi(a,b,t)f(t)dt , a: = 1 ... 30, b: = 0 ... 50,
Nab:=W(a,b) .
Liste des programmes from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): return sin(2*pi*t/10)+sin(2*pi*t/50) plt.figure(' ') plt.title(' ', size=12) y=[S(t) for t in arange(0,250,1)] x=[t for t in arange(0,250,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49, 49) fig = plt.figure("-:2- ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z, 100) plt.figure() q=[w(2,i) for i in y] p=[i for i in y] plt.plot(p,q,label='w(2,b)') q=[w(15,i) for i in y] plt.plot(p,q,label='w(15,b)') q=[w(30,i) for i in y] plt.plot(p,q,label='w(30,b)') plt.legend(loc='best') plt.grid(True) plt.figure() q=[w(i,13) for i in x] p=[i for i in x] plt.plot(p,q,label='w(a,13)') q=[w(i,17) for i in x] plt.plot(p,q,label='w(a,17)') plt.legend(loc='best') plt.grid(True) plt.show()

Graphique du signal.
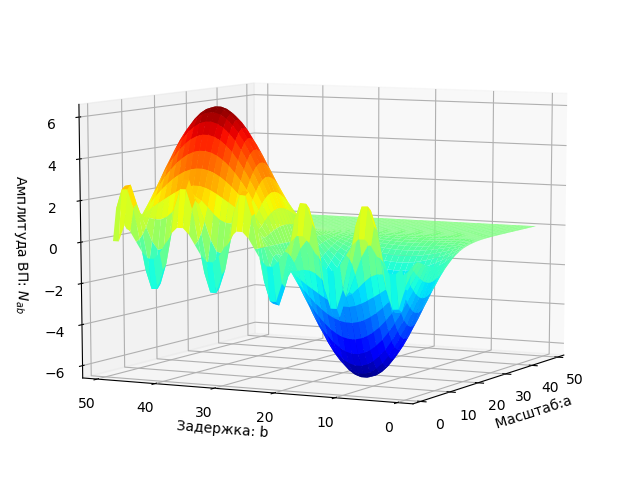
Le tracé du spectre à deux paramètres W (a, b) est affiché comme une surface dans un espace tridimensionnel.
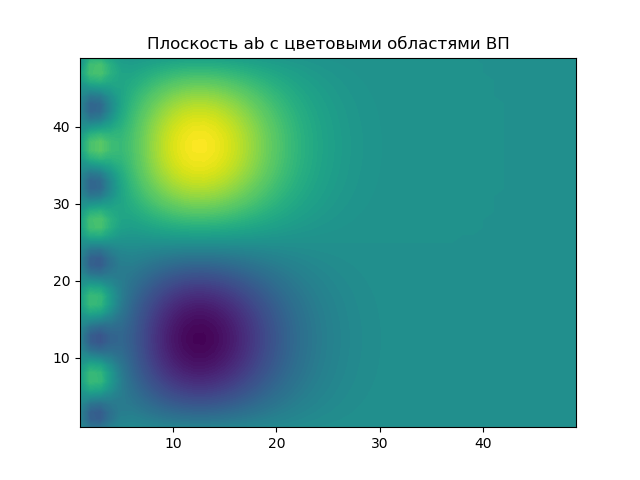
Le plan des paramètres a, b sur lequel les résultats de l'EP sont mis en évidence dans des zones colorées.

Le graphique montre les «coupes» du spectre d'ondelettes pour deux valeurs du paramètre a. Avec un paramètre relativement petit de l'échelle de temps a, par
a1=2(a1:1/ omega2) , la section transversale du spectre ne transporte des informations que sur la composante haute fréquence du signal, filtrant (supprimant) sa composante basse fréquence.
Comme une augmentation, l'extension de la fonction de base
psi( fract−ba) , donc, rétrécissant son spectre, et rétrécissant la bande passante de la "fenêtre" de fréquence. En conséquence, lorsque
a2=15(a2:1/ omega1) la section efficace du spectre n'est qu'une composante basse fréquence du signal.
Avec une nouvelle augmentation de a, la bande de fenêtre diminue toujours et le niveau de cette composante basse fréquence diminue à une composante constante (pour a> 25), qui est égale à zéro pour le signal analysé.

Le graphique montre les sections du spectre d'ondelettes W (a, b) caractérisant
spectre de signal actuel à
b1=13 et
b2=17 . Le spectre du signal considéré, contrairement à l'harmonique, contient une composante haute fréquence dans la région des petites valeurs de l'échelle de temps a (a: 1..3), qui correspond à la deuxième composante du signal
A2sin( omega2t) .
Moment rectangulaire.U:=5,t0:=20, tau:=60s(t):= beginvmatrixU,sit0 leqt leqt0+ tau0,sinon endvmatrixMHAT(t):= fracd2dt2exp left( frac−t22 right)N:=128, psi(a,b,t):=MHAT left( fractba right),W(a,b):= intN−N psi(a,b,t)f(t)dta:=1..50,b:=0..100,Nba:=W(a,b)Liste des programmes from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): U=5;t0=20;tau=60 if t0<=t<=t0+tau: return U else: return 0 plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,120,1)] x=[t for t in arange(0,120,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,100,1) y = arange(1,100,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(99, 99) fig = plt.figure("3D- ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z,100) plt.show()
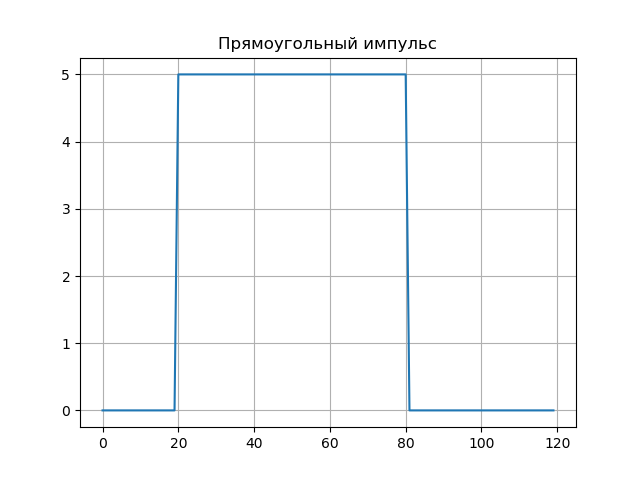


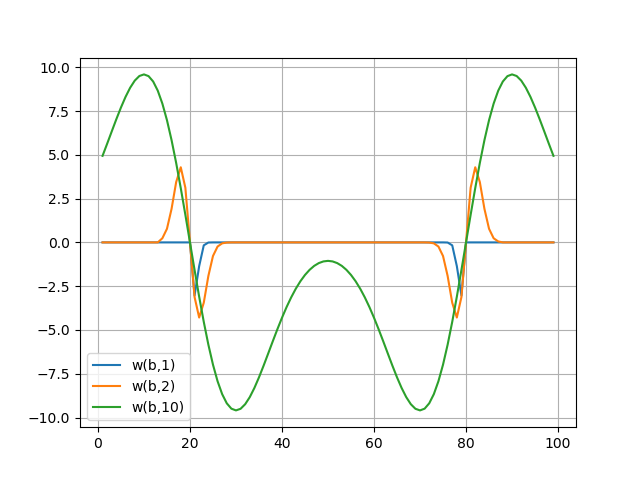
Les spectres d'ondelettes sont représentés sur des graphiques, le spectre d'ondelettes transmet bien les caractéristiques subtiles du signal - ses sauts sur les échantillons b = 20 et b = 80 (pour a: 1..10).
Conclusions
Cette publication est de nature pédagogique, elle fournit des informations de base sur l'analyse des ondelettes en général, et des exemples simples dans le langage de programmation de haut niveau Python librement distribué montrent les caractéristiques de l'analyse en ondelettes continue avec une visualisation graphique 3D et 2D étendue.
PS L'auteur ne diminue pas les avantages inconditionnels de l'analyse en ondelettes utilisant Matlab à la fois en termes de nombre d'ondelettes et de vitesse. Mais en Python, il y a encore de la place pour de nouveaux développements: scipy.signal et PyWavelets.