Tout le monde dans l'industrie informatique sait combien il est difficile d' évaluer la date limite d'un projet. Il est difficile d'évaluer objectivement le temps qu'il faudra pour résoudre une tâche difficile. L'une de mes théories préférées est que ce n'est qu'un artefact statistique.

Supposons que vous évaluiez un projet à 1 semaine. Supposons qu'il y ait trois résultats tout aussi probables: soit cela prendra 1/2 semaine, soit 1 semaine, soit 2 semaines. Le résultat médian est en fait le même que l'estimation: 1 semaine, mais la valeur moyenne (aka moyenne, aka valeur attendue) est de 7/6 = 1,17 semaine. Le score est en réalité calibré (impartial) pour la médiane (qui est 1), mais pas pour la moyenne.

Un modèle raisonnable pour le «facteur d'inflation» (temps réel divisé par le temps estimé) serait quelque chose comme une distribution log - normale . Si l'estimation est égale à une semaine, nous simulons le résultat réel sous la forme d'une variable aléatoire distribuée conformément à la distribution log-normale pendant environ une semaine. Dans une telle situation, la médiane de la distribution est exactement d'une semaine, mais la valeur moyenne est beaucoup plus grande:



Si nous prenons le logarithme du coefficient d'inflation, nous obtenons une distribution normale simple avec un centre d'environ 0. Cela suppose un coefficient d'inflation médian de 1x, et, comme vous l'espérez, souvenez-vous, log (1) = 0. Cependant, dans divers problèmes, il peut y avoir différentes incertitudes autour de 0. On peut les modéliser en modifiant le paramètre σ, qui correspond à l'écart type de la distribution normale:



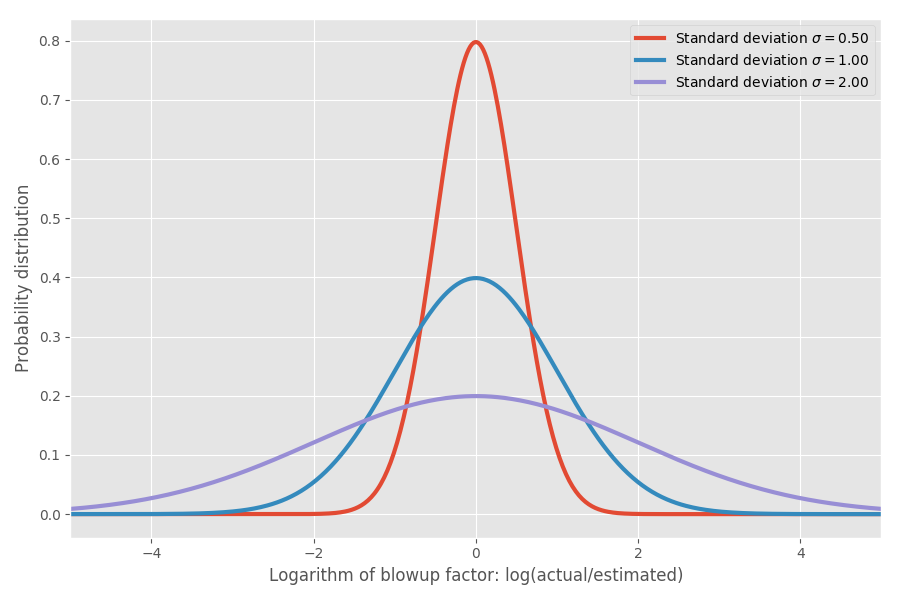
Juste pour montrer les nombres réels: lorsque log (réel / estimé) = 1, alors le coefficient d'inflation exp (1) = e = 2,72. Il est également probable que le projet s'étirera jusqu'à exp (2) = 7,4 fois et qu'il se terminera à exp (-2) = 0,14, soit 14% du temps estimé. Intuitivement, la raison pour laquelle la moyenne est si élevée est que les tâches qui s'exécutent plus rapidement que prévu ne peuvent pas compenser les tâches qui prennent beaucoup plus de temps que prévu. Nous sommes limités à 0, mais pas limités dans l'autre sens.

Est-ce juste un modèle? J'aimerais que tu puisses! Mais bientôt, j'arriverai aux données réelles et sur certaines données empiriques, je montrerai qu'en fait, cela correspond assez bien à la réalité.

Estimation des délais de développement logiciel

Jusqu'à présent, tout va bien, mais essayons vraiment de comprendre ce que cela signifie en termes d'estimation des délais de développement logiciel. Supposons que nous examinions un plan de 20 projets logiciels différents et essayions d'évaluer le temps qu'il faudra pour les réaliser tous .

C'est là que la moyenne devient décisive. Les moyennes s'additionnent, mais il n'y a pas de médiane. Par conséquent, si nous voulons avoir une idée du temps qu'il faudra pour terminer la somme de N projets, nous devons examiner la valeur moyenne. Supposons que nous ayons trois projets différents avec le même σ = 1:


Notez que les moyennes s'additionnent et 4,95 = 1,65 * 3, mais pas les autres colonnes.

Ajoutons maintenant trois projets avec différents sigma:


Les moyennes continuent de prendre forme, mais la réalité n'est même pas proche de l'estimation naïve de 3 semaines à laquelle vous vous attendiez. Notez qu'un projet très incertain avec σ = 2 domine le reste en temps d'achèvement moyen. Et pour le 99e centile, non seulement il domine, mais il absorbe littéralement tous les autres. Nous pouvons donner un exemple plus large:


Là encore, la seule tâche désagréable est principalement dominante dans le calcul de l'estimation, au moins pour 99% des cas. Même dans le temps moyen, un projet fou prend finalement environ la moitié du temps consacré à toutes les tâches, bien qu'ils aient des valeurs similaires en termes de médiane. Par souci de simplicité, j'ai supposé que toutes les tâches ont la même estimation de temps, mais des incertitudes différentes. Les mathématiques sont enregistrées lorsque les termes changent.

C'est drôle, mais j'ai depuis longtemps ce sentiment. L'ajout de notes fonctionne rarement lorsque vous avez beaucoup de tâches. Au lieu de cela, recherchez les tâches qui présentent le plus d'incertitude: ces tâches domineront généralement le temps d'exécution moyen.

Le diagramme montre la moyenne et le 99e centile en fonction de l'incertitude (σ):



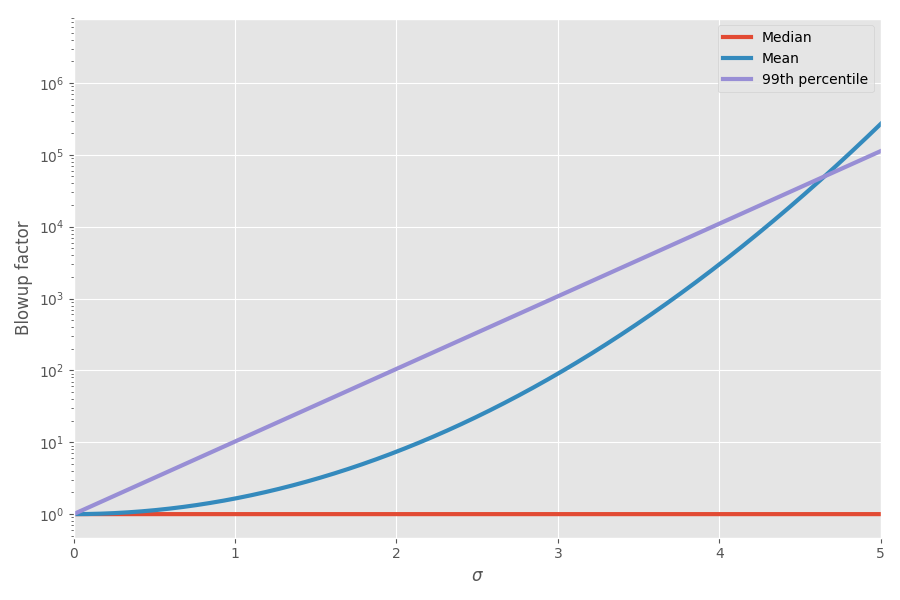
Maintenant, les mathématiques ont expliqué mes sensations! J'ai commencé à en tenir compte lors de la planification des projets. Je pense vraiment que l'ajout d'estimations des délais pour les tâches est très trompeur et crée une fausse image du temps que prendra tout le projet, car vous avez ces tâches biaisées folles qui finissent par prendre tout le temps.

Où sont les preuves empiriques?

Pendant longtemps, je l'ai gardé dans ma tête dans la section «modèles de jouets curieux», pensant parfois que c'est une belle illustration du phénomène du monde réel. Mais un jour, en me promenant dans le réseau, je suis tombé sur un ensemble intéressant de données sur l'évaluation du calendrier des projets et du temps réel pour les achever. Fiction!

Faisons un diagramme de dispersion rapide du temps estimé et réel:



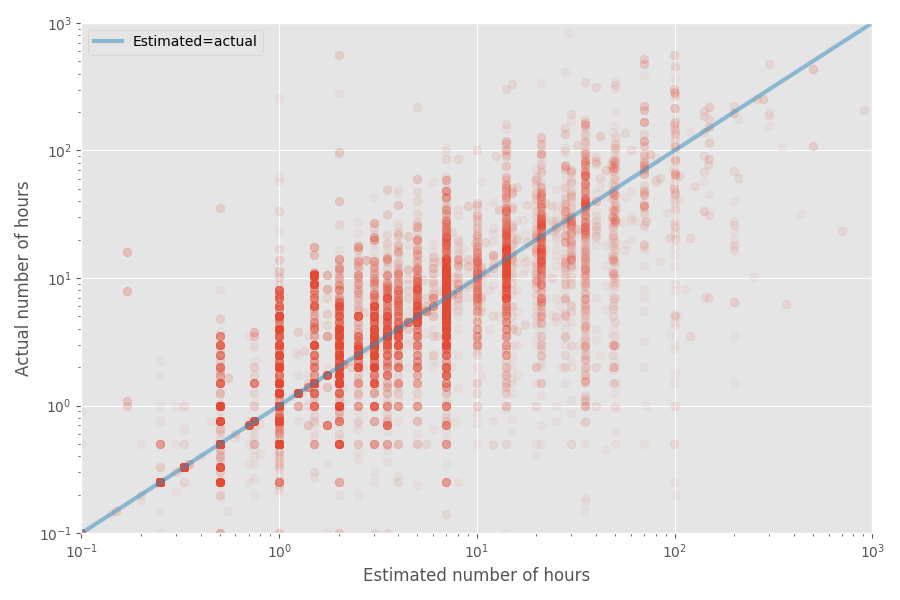
Le taux d'inflation médian pour cet ensemble de données est de 1X, tandis que le coefficient moyen est de 1,81x. Encore une fois, cela confirme le sentiment que les développeurs évaluent bien la médiane, mais la moyenne est beaucoup plus élevée.

Regardons la distribution du coefficient d'inflation (logarithme):



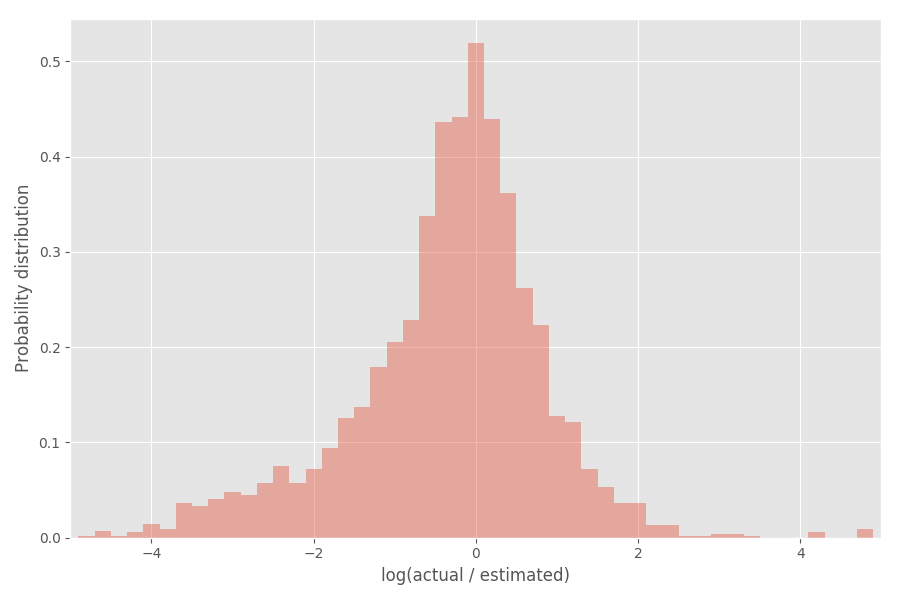
Comme vous pouvez le voir, il est plutôt bien centré autour de 0, où le coefficient d'inflation exp (0) = 1.

Prenez les outils statistiques

Je vais maintenant imaginer un peu les statistiques - n'hésitez pas à sauter cette partie si cela ne vous intéresse pas. Que pouvons-nous conclure de cette distribution empirique? Vous pouvez vous attendre à ce que les logarithmes du taux d'inflation soient distribués selon la distribution normale, mais ce n'est pas entièrement vrai. Notez que σ lui-même est aléatoire et varie pour chaque projet.

Une façon pratique de modéliser σ est qu'ils sont sélectionnés à partir de la distribution gamma inverse . Si nous supposons (comme précédemment) que le logarithme des coefficients d'inflation est distribué conformément à la distribution normale, alors la distribution "globale" des logarithmes des coefficients d'inflation se termine par la distribution de Student .

Nous appliquons la distribution des étudiants à la précédente:



Converge décemment, à mon avis! Les paramètres de distribution des élèves déterminent également la distribution gamma inverse des valeurs de σ:



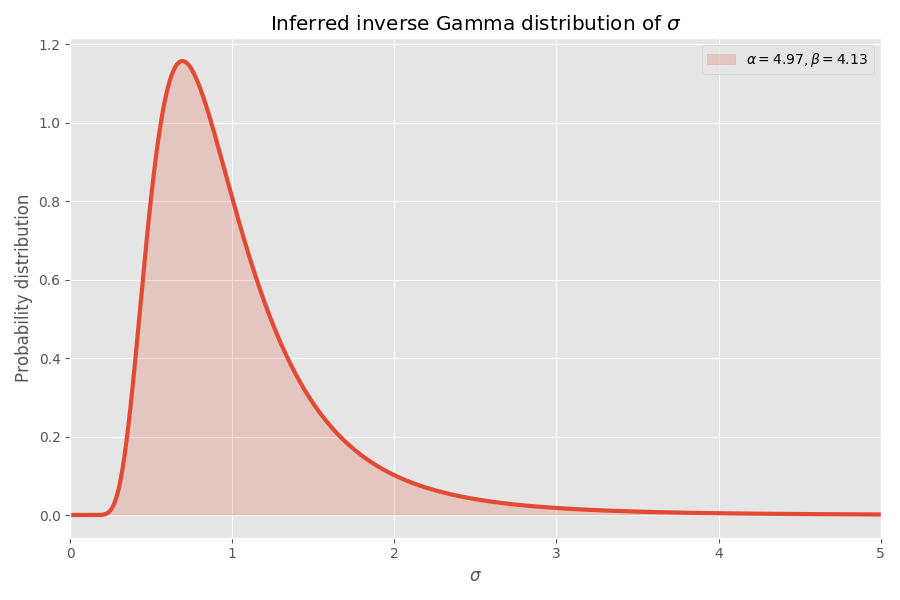
Notez que les valeurs de σ> 4 sont très improbables, mais lorsqu'elles se produisent, elles provoquent une explosion moyenne de plusieurs milliers de fois.

Pourquoi les tâches logicielles prennent toujours plus de temps que vous ne le pensez

En supposant que cet ensemble de données est représentatif du développement logiciel (douteux!), Nous pouvons tirer quelques conclusions supplémentaires. Nous avons des paramètres pour la distribution de Student, donc nous pouvons calculer le temps moyen nécessaire pour terminer la tâche sans connaître σ pour cette tâche.

Alors que le taux d'inflation médian de cet ajustement est 1x (comme précédemment), le taux d'inflation de 99% est 32x, mais si vous passez au 99,99e centile, c'est 55 millions ! Une interprétation (gratuite) est que certaines tâches sont finalement impossibles. En fait, ces cas extrêmes ont un impact si énorme sur la moyenne que le taux d'inflation moyen d' une tâche devient infini . C'est une très mauvaise nouvelle pour quiconque essaie de respecter les délais!

Résumé

Si mon modèle est correct (grand si), alors voici ce que nous pouvons découvrir:

• Les gens estiment bien le temps médian pour terminer une tâche, mais pas la moyenne.
  
• La durée moyenne est beaucoup plus grande que la médiane du fait que la distribution est déformée (distribution lognormale).
  
• Lorsque vous ajoutez des notes pour n tâches, les choses empirent.
  
• Les tâches de la plus grande incertitude (plutôt de la plus grande taille) peuvent souvent dominer dans le temps moyen requis pour terminer toutes les tâches.
  
• Le temps d'exécution moyen d'une tâche dont nous ne savons rien est en fait infini .

Remarques

• De toute évidence, les résultats sont basés sur un seul ensemble de données que j'ai trouvé sur Internet. D'autres ensembles de données peuvent donner des résultats différents.
  
• Mon modèle, bien sûr, est également très subjectif, comme tout modèle statistique.
  
• Je serais heureux d'appliquer le modèle à un ensemble de données beaucoup plus grand pour voir à quel point il est stable.
  
• J'ai suggéré que toutes les tâches sont indépendantes. En fait, ils peuvent avoir une corrélation qui rendra l'analyse beaucoup plus ennuyeuse, mais (je pense) aboutir à des conclusions similaires.
  
• La somme des valeurs distribuées lognormalement n'est pas une autre valeur distribuée lognormalement. C'est la faiblesse de cette distribution, car vous pouvez affirmer que la plupart des tâches sont simplement la somme des sous-tâches. Ce serait bien si notre distribution était durable .
  
• J'ai supprimé de petites tâches de l'histogramme (le temps estimé est inférieur ou égal à 7 heures), car elles faussent l'analyse et il y a eu une étrange vague d'exactement 7.
  
• Le code est sur Github , comme d'habitude.