Bonjour, cher lecteur! Il s'agit du deuxième article traduit d'une série d'articles sur la création du moteur physique par Chris Hecker. Si vous ne vous êtes pas encore familiarisé avec le premier , je vous recommande de le faire, car tout deviendra immédiatement clair. Merci beaucoup d'avoir soutenu la première traduction: c'est très encourageant de travailler de plus en plus! Bonne lecture!

Physique, partie 2, effets angulaires

Je voulais juste soutenir la porte avec quelque chose de lourd pour qu'un intrus ne vienne pas. Suis-je demander beaucoup? Je veux que sa voiture se renverse et explose dans un endroit précis. Je veux que les énormes engrenages se bloquent avant de m'aplatir. Et je veux construire à la hâte une chose qui ressemble à une balançoire, afin de catapulter un joli cadeau lumineux à travers le mur de la forteresse du château. Qui peut m'empêcher de traduire tout cela en réalité? Vous supposez que mon adversaire est dans le monde du jeu, mais en réalité - un programmeur du moteur physique, car tout ce qui précède est basé sur l'effet angulaire. Vous pouvez compter sur les doigts les jeux où les effets de coin sont implémentés, sans oublier d'en trouver au moins un dans lequel cela se fait correctement.

La raison principale pour laquelle les effets angulaires (ou autrement rotatifs) ne sont pas implémentés dans les jeux aujourd'hui est que les programmeurs pensent que la physique qui décrit le mouvement de rotation est trop compliquée à comprendre et à traduire dans la réalité. Dans les cours de physique au lycée (où nous avons tous appris la deuxième loi de Newton), ils ne parlent généralement pas des effets de rotation, et il n'est pas tout à fait évident comment passer de la force appliquée à l'objet à la rotation de cet objet. Bien sûr, la dynamique du mouvement de rotation est un peu plus difficile à comprendre que la dynamique du mouvement linéaire, mais elle est plus simple qu'il n'y paraît. Quiconque peut créer un moteur physique conformément au matériau présenté dans le premier article du cycle parviendra également à inclure les effets angulaires décrits dans cet article. Nous espérons qu'après la publication de cet article, le monde sera rempli de jeux qui utilisent toutes les possibilités et les avantages des effets de coin, ou au moins vous pourrez créer un jeu dans lequel, lorsque vous vous pliez, tirez sur votre ami dans la jambe dans une bataille mortelle.

Brève répétition

Malgré le fait que chacun de mes articles sur un sujet unique, je relis toujours ce que j'ai écrit plus tôt, afin de comprendre où je me suis retrouvé. Je viens de regarder mon premier article sur la physique, et je suis ravi: nous avons réussi à apprendre tellement, et de plus, nous n'avons jamais écrit de code de programme ni lu de littérature supplémentaire! Avant de commencer, rafraîchissons le matériel du dernier article.



Le tableau 1 contient les conclusions les plus importantes pour la dynamique des solides. Il résulte de l'équation 1 que le vecteur de coordonnées (r), le vecteur de vitesse (v) et le vecteur d'accélération (a) sont liés par des dérivées (et par des intégrales, si nous lisons dans l'ordre inverse). Pour rappel, nous marquons la différenciation temporelle par un nombre premier (r '). r 'est identique à dr / dt, et r' 'est identique à la dérivée seconde. De l'équation 2, il s'ensuit que la force est associée à un moment linéaire (le produit de la masse et de la vitesse), à ​​la masse et à l'accélération. La définition du centre de masse peut être obtenue à partir de l'équation 3 (c'est le point où toutes les masses et distances s'équilibrent). L'équation 4 indique que la quantité de mouvement linéaire totale d'un solide est la somme de tous ses moments, qui, à notre chance, sont simplement égaux à la quantité de mouvement du centre de masse (CM). L'équation 5 est un vrai bijou. Il utilise l'équation 4 pour démontrer que l'accélération du centre de masse d'un objet est liée à la force totale (le vecteur de la somme de toutes les forces agissant sur l'objet à un instant donné) à travers une quantité scalaire, la masse de l'objet.

Pour résumer tout ce qui est décrit dans le premier article: nous avons appris que la force totale agissant sur notre centre de masse est égale à la somme de toutes les forces appliquées au corps (y compris la force de gravité, le wagon du méchant, une explosion à proximité, la poussée de notre moteur, etc. .). Après cela, nous avons divisé ce vecteur somme par la masse corporelle afin d'obtenir l'accélération CM, puis intégré l'accélération temporelle pour obtenir la vitesse et les coordonnées du corps.

L'équation 5 n'est qu'un chef-d'œuvre! Vous verrez qu'il n'y a pas de concept de points d'application de forces au corps, et c'est un point clé pour déterminer comment le corps tournera sous leur action. L'équation 5 est correcte. En fait, il est excellent pour trouver une accélération linéaire. Il nous manque la moitié de la bataille. Mais tout d'abord ...

Quel est ton angle?

Dans le premier article, la rotation était ignorée, nous n'avions donc besoin que d'un vecteur de rayon et de sa dérivée pour décrire la configuration de notre corps en 2D. Ajoutons maintenant une autre valeur cinématique, l'orientation (indiquée par la lettre majuscule oméga - Ω), afin de travailler avec les effets de coin. Pour définir Ω, nous devons choisir le système de coordonnées par rapport au solide et au système de coordonnées du monde du jeu, et la valeur de Ω sera égale à la différence d'angles entre eux en radians, comme le montre la figure 1.



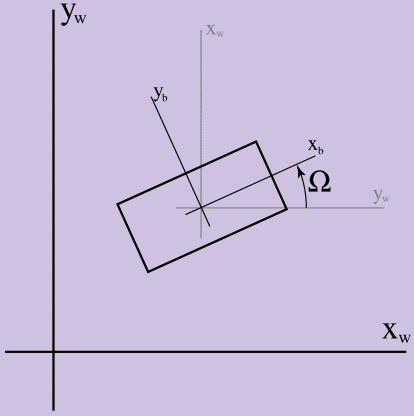Figure 1. Définition de Ω

Dans la figure, les axes xw, yw sont les axes de coordonnées du monde du jeu, et xb, yb sont les axes de coordonnées du solide. Ω est supérieur à 0 s'il est compté dans le sens antihoraire. Il est important ici de clarifier pourquoi nous étudions la dynamique du monde bidimensionnel avant de passer au tridimensionnel: l'orientation en 2D est une quantité scalaire (l'angle entre les systèmes de coordonnées en radians), alors que déterminer l'orientation dans le monde tridimensionnel est beaucoup plus difficile.

À mesure que le corps tourne, la valeur de Ω change. Ce changement nous amène à une autre cinématique - la vitesse angulaire (désignée par la lettre minuscule oméga - ω). Contrairement aux coordonnées et à la vitesse linéaire du corps, nous ne désignons pas la vitesse angulaire comme suit - Ω '. Cependant, nous désignons parfois la dérivée de la vitesse par rapport au temps, ou l'accélération angulaire, comme ω '(c'est une autre valeur cinématique) ou comme α (alpha en minuscules). Ne me blâmez pas: je n'ai pas trouvé toutes ces désignations; et dans chaque livre que j'ai lu, il y a de légères différences. Notre contrepartie angulaire pour l'équation 1 est:

$$$$ afficher $$ {d ^ 2 Ω \ sur {dt ^ 2}} = {dω \ sur {dt}} = ω '= α $$ afficher $$

Équation 6

Comme dans l'équation 1, on différencie ω dans le temps pour obtenir α; et si on intègre α dans le temps, on obtient ω, etc. Tout par analogie avec l'article précédent: connaissant l'accélération angulaire de α, on peut l'intégrer deux fois pour obtenir une nouvelle orientation. Mais le point clé ici est de connaître la valeur de α.

Comme vous pouvez l'imaginer, notre objectif pour cet article est de dériver un analogue angulaire pour chacune des équations linéaires du tableau 1, puis, en tenant compte des équations linéaires et angulaires et de la force appliquée à l'objet, nous pouvons calculer son accélération linéaire a et l'accélération angulaire α. Enfin, nous pouvons intégrer numériquement ces accélérations pour trouver de nouvelles positions et orientations de nos corps.

Pour commencer, nous relierons les quantités linéaires et angulaires. Et c'est une astuce assez peu évidente dans laquelle la vitesse angulaire est utilisée. Lors du calcul en dynamique, nous devons souvent trouver la vitesse d'un point arbitraire sur un objet. Par exemple, lorsque nous calculons les collisions de solides, nous devons connaître la vitesse des points de collision afin de comprendre combien ils se heurtent. Si nos corps ne tournent pas, la vitesse de chaque point du corps est la même. Nous pouvons simplement surveiller la vitesse du centre de masse du corps, et ce sera suffisant. Alors que si nos corps tournent, chaque point de ces corps peut avoir une vitesse différente. De toute évidence, nous ne pouvons pas calculer la vitesse d'un nombre infini de points de notre corps rigide, nous avons donc besoin d'une solution différente et meilleure.

L'une des méthodes simples utilisées pour trouver la vitesse linéaire de n'importe quel point à l'intérieur d'un objet utilise la vitesse angulaire de l'objet. Prenons le cas où le corps tourne uniquement autour d'un point fixe O, sans changer les coordonnées du corps. Autrement dit, le corps tourne, mais ne bouge pas. De l'équation 7, il suit comment calculer la vitesse du point B d'un corps en rotation:

$$$$ afficher $$ v ^ B = ωr ^ {OB} _⟂ $$ afficher $$

Équation 7

Nous devons clarifier quelques points dans l'équation 7, passons un peu de temps à ce sujet. Tout d'abord, j'utilise l'indexation supérieure pour montrer quel paramètre appartient à ces points, donc v ^ B est le vecteur vitesse du point B de notre corps. De même, r ^ OB désigne un vecteur tiré du centre de rotation de notre corps O au point B. La drôle de lettre inversée T est "l'opérateur perpendiculaire" qui agit sur le vecteur (comme le vecteur r dans l'équation 7) et le fait pivoter de 90 degrés dans le sens antihoraire des flèches. En d'autres termes, un nouveau vecteur est construit qui est perpendiculaire à l'ancien. Dans un monde à deux dimensions, un vecteur perpendiculaire à (x, y) est juste (-y, x). Vous pouvez facilement vérifier mes mots sur une feuille de papier millimétré. Parlons plus à ce sujet. La magnitude du vecteur perpendiculaire est déterminée par la vitesse angulaire ω et définit la vitesse linéaire v ^ B. En russe, l'équation 7 montre que la vitesse d'un point d'un corps en rotation est calculée en multipliant le vecteur perpendiculaire tiré du centre de rotation par la vitesse angulaire. Comment est-ce que je comprends cela? Eh bien, j'ai lu à ce sujet dans le livre, mais il est évident qu'une telle explication ne suffit pas, alors nous prouvons que c'est vrai.

Prouvons la vérité des conclusions de l'équation 7 en deux étapes. Premièrement, nous prouvons que la valeur du vecteur vitesse résultant est correcte; alors - que sa direction est correcte. Pour la première partie de la preuve, considérons la figure 2.



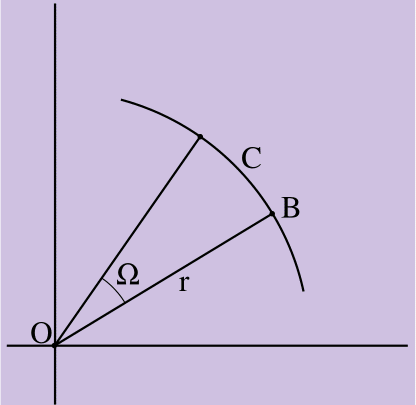Figure 2. C = Ωr

La figure 2 montre la rotation du point B d'un angle égal à Ω radian dans le sens de rotation d'un corps rigide avec un vecteur de rayon de longueur r dirigé du centre de rotation du corps O vers le point B.B a dépassé la longueur de l'arc C, où C = Ωr d'après la définition des radians. (Une mesure radian d'un angle est une mesure d'un arc délimité par un rayon d'un cercle. La circonférence d'un cercle est C = 2πr car la mesure radian d'un arc de cercle est 2π [ou 360 degrés]).

La vitesse d'un point est un changement de ses coordonnées dans le temps. Par conséquent, nous pouvons trouver la vitesse du point B - en d'autres termes, la grandeur du vecteur vitesse - en différenciant les équations du mouvement par rapport au temps. C = Ωr est l'équation du mouvement.

$$

$${d (Ωr) \ over {dt}} = {dΩ \ over {dt}} r = ωr$$

Le rayon est retiré du signe de différenciation, car il s'agit d'une constante (le point B tourne simplement, sans déplacement linéaire), et la dérivée temporelle Ω est ω de l'équation 6. Par conséquent, la magnitude du vecteur B est le vecteur vitesse ωr.

En considérant l'équation 7, nous remarquons que la magnitude du vecteur vitesse est correcte, car la perpendiculaire n'affecte pas la longueur du vecteur et r ^ OB est un vecteur rayon dirigé de O à B. Fuh, nous sommes à mi-chemin.

Afin de vérifier que la direction du vecteur vitesse dans l'équation 7 est correcte, commençons par nous assurer que le vecteur vitesse doit être perpendiculaire au vecteur rayon. Cette hypothèse est compréhensible intuitivement, car un point tournant autour d'un autre point donné ne peut se déplacer que perpendiculairement au vecteur entre ces points. Il ne peut pas s'approcher du centre de rotation ou s'en éloigner, ou ce mouvement cessera simplement d'être une rotation. Nous pouvons soutenir notre hypothèse avec des calculs pour les vecteurs, mais je suis coincé dans un certain cadre pour le volume de l'article, nous supposerons donc que notre hypothèse est correcte. (Si vous êtes impatient de le prouver par vous-même, différenciez le produit scalaire d'un vecteur de longueur fixe par lui-même.)

Enfin, nous devons nous assurer que le vecteur est correctement marqué, car la figure montre deux vecteurs d'égale longueur perpendiculaires au rayon: v et -v. Puisque la valeur de Ω est mesurée dans le sens antihoraire, ω> 0 lorsque le point tourne dans le sens horaire. Les points perpendiculaires dans le sens horaire, tout comme le vecteur rayon. La figure 3 montre les conclusions de l'équation 7:



Figure 3. Relation entre la vitesse linéaire et angulaire

Compléter l'équation 7 pour décrire la rotation des corps en mouvement. Nous considérons le mouvement d'un corps solide comme un simple mouvement du centre de rotation du corps et une simple rotation du reste du corps autour de ce point. Pour ceux qui sont intéressés, il s'agit du théorème de Schal sur la classification des mouvements.

Le théorème de Chall divise notre mouvement en deux composantes - linéaire et angulaire. Soit le centre de rotation du corps O le seul point mobile, puis on utilise ω pour calculer la rotation autour du point O, et cela nous donne la forme générale de l'équation 7:

$$$$ afficher $$ v ^ B = v ^ O + ωr ^ {OB} _⟂ $$ afficher $$

Équation 9

L'équation 9 dit que nous pouvons calculer la vitesse de n'importe quel point d'un corps en mouvement en utilisant la vitesse linéaire du centre de rotation du corps et, en plus, la vitesse acquise pendant la rotation du corps.

Raison de notre impulsion

Nous pouvons maintenant écrire un analogue angulaire de l'équation 2, l'équation de la force. On commence par déterminer l'impulsion angulaire, L ^ AB d'un point B donné, autour d'un autre point A:

$$

$${L} ^ {AB} = {\ vec r} ^ {AB} \ times {\ vec p} ^ B$$

Équation 10

Le moment de l'impulsion d'un point diffère de l'impulsion linéaire d'un point en ce que la version angulaire de l'équation prend en compte la position du corps dans l'espace. Il en résulte que l'impulsion angulaire d'un point doit être mesurée pour un endroit différent dans le monde du jeu, contrairement à l'impulsion linéaire, qui est déterminée pour un point donné (le produit de sa masse et de sa vitesse). Ceci est illustré par l'indexation supérieure de l'équation 10. La notation L ^ AB indique que le moment angulaire est mesuré pour le point B à partir du point A (centre de rotation du corps). Imaginez une flèche pointant du point A au point B. Cette flèche est un vecteur de rayon entre deux points, cela signifie r ^ AB. Ainsi, la quantité de mouvement angulaire d'un point est un produit scalaire d'un vecteur de quantité de mouvement linéaire et d'un vecteur de rayon perpendiculaire à celui-ci. Cette opération est appelée «produit scalaire à perpendiculaire», et est un analogue 2D pour le produit vectoriel 3D, mais nous en discuterons une autre fois.

Si vous décrivez graphiquement ce qui découle de l'équation 10, sur papier - comme je l'ai fait dans la figure 4 - vous verrez qu'il détermine la mesure de la façon dont le moment linéaire du point B «tourne autour» A.



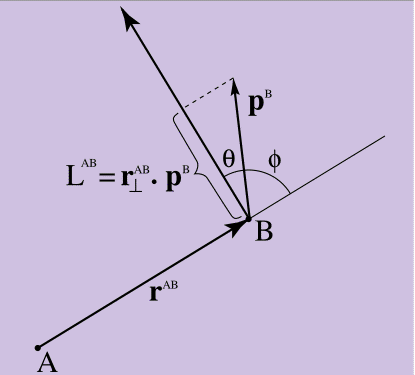Figure 4. Moment d'impulsion

Tout est correct si l'impulsion du point B pointe directement vers le point A, équation 10 = 0 (puisque la perpendiculaire à r forme un angle droit avec p, et le produit scalaire sera 0). Plus l'élan B est dirigé perpendiculairement à A, plus l'élan est important. Comme on peut le voir sur la figure 4, le produit scalaire de l'équation 10 a pour paramètre le cosinus de l'angle θ compris entre la perpendiculaire r ^ AB à p ^ B. Si vous le regardez d'un autre côté, la magnitude du produit scalaire est donnée par le sinus de l'angle φ entre l'original, non perpendiculaire r ^ AB et p ^ B (le sinus est une autre clé pour démêler la connexion entre le vecteur et le produit scalaire). L'équation 10 donne une mesure de la quantité de la quantité de mouvement du point B qui "regarde" dans le "sens de rotation" par rapport au point A.

De plus, comme nous avons utilisé la dérivée du moment linéaire pour déterminer la force, nous utiliserons la dérivée du moment angulaire pour déterminer le jumeau angulaire de la force - le moment de la force (indiqué par la lettre minuscule tau - τ).

$$

$$τ ^ {AB} = {dL ^ {AB} \ over dt} = {d ({\ vec r} ^ {AB} \ times {\ vec p} ^ B) \ over dt} = \ vec r ^ { AB} \ fois ma ^ B = \ vec r ^ {AB} \ fois F ^ B$$

Équation 11

Pour économiser de l'espace, j'ai un peu triché dans l'équation 11, sautant quelques étapes difficiles qui impliquaient de trouver des dérivés. De ce qui précède, il s'ensuit que le moment de force est associé à la force à un certain point à travers un produit scalaire.

Enfin, nous avons obtenu une équation dynamique qui utilise le point d'application de la force, qui était auparavant ignoré dans les équations de moment linéaire. L'équation 11 utilise un produit scalaire avec une perpendiculaire comme mesure de la quantité de force appliquée au point B qui tourne autour du point A; cette «force de rotation» est appelée moment de force. L'équation 11 permet de trouver la valeur numérique du moment de force - et donc du moment angulaire, si l'on intègre le moment de force, en connaissant la force appliquée et le point d'application.

Cependant, nous n'avons toujours pas reçu l'équation de la relation entre le moment de la force et les amplitudes angulaires de la cinématique dont nous avons besoin pour faire tourner l'objet autour de son axe - comme l'accélération angulaire, la vitesse angulaire ou l'orientation. Par conséquent, nous ne pouvons pas avancer avant de dériver quelques équations supplémentaires.

Le moment que nous attendions tous

Avant de faire un lien entre la dynamique et la cinématique, nous devons déterminer le moment angulaire total, par analogie avec la façon dont nous avons déterminé le moment linéaire total dans l'équation 4. Je n'ai pas oublié l'équivalent angulaire du centre de masse dans l'équation 3; nous le verrons dans l'équation du moment angulaire total.

La quantité de mouvement angulaire totale près du point A est désignée par L ^ AT et est déterminée par l'équation 12:

$$

$$L ^ {AT} = {\ sum _ {i} {} {\ vec r ^ {Ai} \ times p ^ i}} = {\ sum _ {i} {\ vec r ^ {Ai} \ times m ^ iv ^ i}}$$

Équation 12

L'équation 12 est la somme de tous les moments angulaires de tous les points du corps, mesurée par rapport au point A. Sur le côté droit, j'ai utilisé la définition du moment linéaire afin de représenter p ^ i comme le produit de la masse et de la vitesse (mv). Cela me sera utile à l'avenir afin de faire de l'équation 12 quelque chose avec un caractère appliqué plus prononcé. L'équation dit que pour trouver le moment angulaire total pour notre objet, il est nécessaire de additionner le moment angulaire de tous ses points. Pour un corps solide constitué de faces (et non de points séparés), il est nécessaire de calculer l'intégrale, pour une somme non discrète.

Heureusement, nous pouvons simplifier nos calculs en introduisant une nouvelle quantité appelée «moment d'inertie», similaire à la façon dont nous avons introduit le centre de masse pour simplifier l'équation de la quantité de mouvement totale. Rappelons que, grâce à l'équation 7, nous pouvons trouver la vitesse d'un point à travers la vitesse angulaire. Soit le point A de l'équation 12 le centre de rotation de l'équation 7, et l'indice de sommation i de l'équation 12 le point B de l'équation 7, alors il est possible de convertir l'équation 7 en équation 12. On obtient:

$$

$$L^{AT} = \sum _{ i} {\vec r ^{Ai} \times m^i ω \vec r^{Ai}} = ω {\sum _{ i} {m^i \vec r^{Ai} \times \vec r ^{Ai}}} = ω \sum_{ i} {m^i (\vec r ^{Ai})^2} = ωI^A$$

Équation 13 Je vais

écrire l'équation 13 plus en détail, étape par étape. Tout d'abord, nous remplaçons l'équation 7 par 12 afin d'obtenir la somme de l'équation 13. Ce remplacement nous permet de décrire la quantité de mouvement angulaire en utilisant la vitesse angulaire. Ensuite, nous prenons ω pour la somme, car elle est égale pour tous les points du solide (la vitesse angulaire est déterminée pour tout le corps, et non pour chaque point séparément), et notons la masse avec l'indice i à gauche, afin de voir plus clairement le rayon du produit scalaire -vecteurs pour eux-mêmes. Ce produit scalaire est égal au carré de la longueur du vecteur rayon (le produit scalaire de tout vecteur en lui-même = le carré de sa longueur. N'oubliez pas que l'opérateur perpendiculaire ne change pas la longueur du vecteur.). Enfin, nous écrivons I ^ A pour désigner le moment d'inertie autour du point A.

Le moment d'inertie d'un solide bidimensionnel est un très bon nombre, car les points qui composent le corps ne peuvent pas changer de masse ou s'éloigner du centre de rotation. En conséquence de ces deux propriétés, la somme de l'équation 13 est une constante pour chaque corps, nous pouvons donc la calculer. Parlant en russe, I ^ A est la somme des distances au carré du point A à tous les autres points du corps, et chacune de ces distances est mise à l'échelle en fonction de la masse de chaque point. Tout comme pour le centre de masse - si le corps est plus solide que composé de points discrets, alors les sommes se transformeront en intégrales. Et le moment d'inertie restera le même en ampleur et aura la même signification physique.

Déterminer le moment d'inertie près d'un point est détaillé, mais pensez à I ^ A comme la mesure de la difficulté à faire tourner le corps autour du point A. Par exemple, imaginez un crayon (crayon plat). Si nous mesurons le moment d'inertie près du centre du crayon, nous obtenons une certaine valeur égale à la somme des carrés des distances mises à l'échelle en fonction de la masse de chaque point. Alors que si nous mesurons l'inertie à la pointe du même crayon, nous obtenons une valeur plus grande, car plus les points de masse sont éloignés, plus la valeur des carrés de leurs distances est grande. Ici, nous formulerons mathématiquement ce qui nous est intuitif: faire tourner un crayon autour de son centre est beaucoup plus facile (lire, cela demande moins d'effort) que le faire tourner autour d'une des extrémités.

Enfin, nous sommes prêts à établir un lien entre les équations angulaires de la dynamique et les équations angulaires de la cinématique. Si nous différencions l'équation 13, nous obtenons le moment de force total à gauche, et le produit du moment d'inertie et de l'accélération angulaire à droite (I ^ A est une constante, nous la mettons en dehors du signe de différenciation):

$$

$$τ^{AT} = {dL^{AT} \over dt} = {d( I^A ω) \over dt} = I^A ω = I^A α$$

Équation 14

Cette équation est l'équivalent angulaire de l'équation 5; en fait, c'est F = ma pour la dynamique angulaire. Il s'agit de l'équation de la connexion du moment de force total et de l'accélération angulaire du corps à travers le moment d'inertie scalaire. Si nous connaissons le moment de force exercé sur notre corps, nous pouvons trouver son accélération angulaire, puis la vitesse angulaire et l'orientation dans l'espace grâce à l'intégration - divisant le moment de force par le moment d'inertie.

Algorithme dynamique

Il nous voit à peine dans ce tourbillon d'équations, mais toutes en font partie intégrante. Nous avons dérivé suffisamment d'équations pour obtenir la magnifique dynamique d'un monde à deux dimensions avec des forces et des moments de forces arbitrairement donnés déplaçant et tournant nos objets. Comment utiliser ces équations? Voici l'algorithme de base:

1. Trouvez la valeur du centre de masse et le moment d'inertie au centre de masse.
2. Définissez les coordonnées initiales du corps, son orientation dans l'espace, ses vitesses linéaires et angulaires.
3. Prendre en compte toutes les forces agissant sur le corps et les points de leur application.
4. Trouvez la résultante de toutes les forces et divisez-la par la masse du corps afin de trouver l'accélération linéaire du centre de masse (équation 5).
5. , , , ( 11).
6. ( 14).
7. , , ( ).
8. , 3.

Dans l'algorithme ci-dessus, il n'y a que deux étapes que je n'ai pas expliquées. Tout d'abord, comment calculer le moment d'inertie à l'étape 1 pour un objet solide? Deuxièmement, comment résoudre le problème avec les forces de l'étape 3? La réponse à la première question se trouve dans un exemple de code simple, que je laisserai dans l'application à la fin de cet article (vous intégrerez l'objet par sa zone). De nombreux livres sur la dynamique contiennent le moment d'inertie calculé pour les formes d'objets fréquemment rencontrées dans l'application à la toute fin, vous n'avez donc pas à les afficher vous-même à chaque fois.

La réponse à la question de savoir comment calculer les forces à partir de l'étape 3 dépend de l'application, mais je donnerai quelques recommandations générales. Premièrement, des forces telles que la gravité, toujours dirigées dans une direction (vers le bas, dans le cas de la gravité), ne créent pas un moment de force, car elles tirent tous les points en même temps dans la même direction, bien que nous nous appliquons ces forces directement au centre de masse. Des forces similaires à la force élastique sont appliquées à un certain point de l'objet, elles créeront un moment de force, nous les considérons donc dans le cas général. Comme nous l'avons vu dans le premier article, la force de frottement est la même force dirigée dans le sens opposé à la vitesse du corps.

Vous pouvez créer un modèle physique simple démontrant la force de frottement, et simplement appliquer une force au centre de masse, ou vous pouvez choisir quelles parties de l'objet appliqueront des forces de frottement, et cela, ce qui peut créer un moment de force agissant sur l'objet. Les forces que les corps subissent dans les collisions sont un peu plus difficiles, et nous les connaîtrons dans le prochain article. Des forces comme la poussée d'un moteur-fusée doivent être considérées comme des forces avec un point d'application (dans ce cas, si l'un des moteurs tombe en panne, vous commencerez à tourner autour de son axe jusqu'à ce que vous ajustiez le volant pour équilibrer le moment de la force!). Si vous voulez quelque chose qui ressemble à des rayons gravitationnels d'un OVNI, alors cette force doit être calculée comme la force de gravité et ne pas créer un moment de force, ou elle doit être appliquée à un point spécifique de l'objet,et tournera-t-il autour de ce point en se levant? Le choix vous appartient. Le point clé est de ne pas avoir peur d'expérimenter différentes forces calculées de différentes manières, car maintenant vous avez un vrai simulateur de graphismes en deux dimensions, essayez différents types de forces!

J'ai laissé tout le code et les liens dont vous avez besoin sur mon site Web car il n'y a plus d'espace. Dans ma simple application, j'ai implémenté l'algorithme de la dynamique d'un monde à deux dimensions, et ajouté également des objets fixés par un ressort; ils tournent autour de leur axe, et parfois même entrent en collision avec des murs, tournent. Mais je vais en parler une autre fois. Suivez le lien pour plus de documentation et une application simple pour Windows 32 et Macintosh.

Très rarement, Chris Hecker ressent l'effet du moment d'inertie, mais il passe généralement assez rapidement. Les forces peuvent être appliquées à checker@bix.com.

Notes du traducteur: un jeu de mots est présenté ici, le sujet de l'article et son contenu sont joués.

Les commentaires PS sont les bienvenus. Vos commentaires peuvent améliorer la qualité du travail. Je vous remercie!

PPS L'auteur de la traduction remercie tout particulièrement les utilisateurs de berez et Vasily Tereshkov pour la révision de la traduction. Je vous remercie!