Réseaux d'antennes adaptatives: comment ça marche? (Bases)

Bonjour.

Ces dernières années, je me suis consacré à la recherche et à la création de divers algorithmes pour le traitement spatial des signaux dans des réseaux d'antennes adaptatifs, et je continue à le faire dans le cadre de mon travail à l'heure actuelle. Ici, je voudrais partager les connaissances et les puces que j'ai découvertes. J'espère que cela sera utile pour les personnes qui commencent à étudier ce domaine du traitement du signal ou tout simplement intéressées.

Qu'est-ce qu'un réseau d'antennes adaptatives?

Un réseau d'antennes est un ensemble d'éléments d'antenne, disposés d'une manière ou d'une autre dans l'espace. Pour simplifier la structure du réseau d'antennes adaptatif, que nous considérerons, peut être représenté sous la forme suivante:


Les réseaux d'antennes adaptatives sont souvent appelés «antennes intelligentes» (antennes intelligentes ). Le réseau d'antennes «intelligent» est constitué par l'unité de traitement du signal spatial et les algorithmes qui y sont implémentés. Ces algorithmes analysent le signal reçu et forment un ensemble de poids$$ $ en ligne $ w_1 ... w_N $ en ligne $ qui déterminent l'amplitude et la phase initiale du signal pour chacun des éléments. La distribution d'amplitude-phase donnée détermine le modèle de directivité de l' ensemble du réseau dans son ensemble. La capacité de synthétiser le diagramme de rayonnement de la forme requise et de le modifier pendant le traitement du signal est l'une des principales caractéristiques des réseaux d'antennes adaptatives, ce qui permet de résoudre un large éventail de problèmes . Mais tout d'abord.

Comment se forme le diagramme de rayonnement?

Un diagramme de rayonnement caractérise la puissance d'un signal rayonné dans une certaine direction. Pour simplifier, nous mettons les éléments du réseau isotropes, c'est-à-dire pour chacun d'eux, la puissance du signal émis ne dépend pas de la direction. L'amplification ou l'atténuation de la puissance rayonnée par le réseau dans une certaine direction est obtenue en raison de l' interférence des ondes électromagnétiques émises par divers éléments du réseau d'antennes. Un modèle d'interférence stable pour EMW n'est possible que s'ils sont cohérents , c'est-à-dire la différence de phase des signaux ne doit pas changer avec le temps. Dans le cas idéal, chacun des éléments du réseau d'antennes devrait émettre un signal harmonique à la même fréquence porteuse$$ $ inline $ f_ {0} $ inline $ . Cependant, en pratique, il est nécessaire de travailler avec des signaux à bande étroite ayant un spectre de largeur finie$$ $ inline $ \ Delta f << f_ {0} $ inline $ .
Laissez tous les éléments AR émettre le même signal avec une amplitude complexe$$ $ en ligne $ x_n (t) = u (t) $ en ligne $ . Ensuite, au niveau du récepteur distant , le signal reçu du nième élément peut être représenté sous une forme analytique :

$$$$ afficher $$ a_n (t) = u (t- \ tau_n) e ^ {i2 \ pi f_0 (t- \ tau_n)} $$ afficher $$

où$$ $ inline $ \ tau_n $ inline $ - retard dans la propagation du signal de l'élément d'antenne au point de réception.
Un tel signal est "quasi-harmonique", et pour satisfaire la condition de cohérence, il est nécessaire que le retard maximum dans la propagation des ondes électromagnétiques entre deux éléments quelconques soit bien inférieur au temps caractéristique du changement d'enveloppe du signal$$ $ en ligne $ T $ en ligne $ , c'est-à-dire$$ $ inline $ u (t- \ tau_n) ≈ u (t- \ tau_m) $ inline $ . Ainsi, la condition de cohérence d'un signal à bande étroite peut s'écrire comme suit:

$$$$ afficher $$ T≈ \ frac {1} {\ Delta f} >> \ frac {D_ {max}} {c} = max (\ tau_k- \ tau_m) $$ afficher $$

où$$ $ inline $ D_ {max} $ inline $ - la distance maximale entre les éléments de l' AR , et$$ $ inline $ avec $ inline $ C'est la vitesse de la lumière.

Lors de la réception d'un signal, une sommation cohérente est effectuée numériquement dans l'unité de traitement spatial. Dans ce cas, la valeur complexe du signal numérique en sortie de ce bloc est déterminée par l'expression:

$$$$ afficher $$ y = \ sum_ {n = 1} ^ Nw_n ^ * x_n $$ afficher $$

Il est plus commode de présenter la dernière expression sous la forme d'un produit scalaire de vecteurs complexes à N dimensions sous forme matricielle:

$$$$ afficher $$ y = (\ textbf {w}, \ textbf {x}) = \ textbf {w} ^ H \ textbf {x} $$ afficher $$

où w et x sont des vecteurs de colonne, et$$ $ inline $ (.) ^ H $ inline $ - opération d' appariement hermitien .

La représentation vectorielle des signaux est l'une des bases lorsque vous travaillez avec des réseaux d'antennes, car évite souvent de lourds calculs mathématiques. De plus, l'identification d'un signal reçu à un certain moment avec un vecteur nous permet souvent d'abstraire d'un véritable système physique et de comprendre ce qui se passe exactement du point de vue de la géométrie.

Afin de calculer le diagramme de directivité du réseau d'antennes, il est nécessaire de "mentalement et systématiquement" exécuter sur lui un ensemble d' ondes planes de toutes les directions possibles. Dans ce cas, les valeurs des éléments du vecteur x peuvent être représentées comme suit:

$$$$ afficher $$ x_n = s_n = \ exp \ {- i (\ textbf {k} (\ phi, \ theta), \ textbf {r} _n) \} $$ afficher $$

où k est le vecteur d'onde$$ $ inline $ \ phi $ inline $ et$$ $ inline $ \ theta $ inline $ - angle azimutal et angle d' élévation caractérisant la direction d'arrivée d'une onde plane,$$ $ inline $ \ textbf {r} _n $ inline $ - coordonnées de l'élément d'antenne,$$ $ inline $ s_n $ inline $ - un élément du vecteur de phasage s d'une onde plane avec le vecteur d'onde k (dans la littérature anglaise, le vecteur de phasage est appelé vecteur de direction). La dépendance du carré de l'amplitude de y sur$$ $ inline $ \ phi $ inline $ et$$ $ inline $ \ theta $ inline $ détermine le diagramme de directivité du réseau d'antennes à la réception pour un vecteur donné de coefficients de poids w .

Caractéristiques du réseau d'antennes

Il est commode d'étudier les propriétés générales du diagramme de rayonnement d'un réseau d'antennes sur un réseau d'antennes équidistant linéaire dans un plan horizontal (c'est-à-dire que le diagramme de faisceau dépend uniquement de l'angle azimutal$$ $ inline $ \ phi $ inline $ ) Il est pratique de deux points de vue: calculs analytiques et présentation visuelle.

Nous calculons le DN pour un vecteur de poids unitaire ($$ $ inline $ w_n = 1, n = 1 ... N $ inline $ ), en suivant l'approche décrite ci - dessus .


En conséquence, nous obtenons:

$$$$ afficher $$ F (\ phi) = | y | ^ 2 = \ frac {\ sin ^ 2 (\ pi \ frac {Nd} {\ lambda} \ sin \ phi)} {\ sin ^ 2 (\ pi \ frac {d} {\ lambda} \ sin \ phi)} $$ display $$

Fréquence du diagramme de rayonnement

Le diagramme de rayonnement résultant du réseau d'antennes est une fonction périodique du sinus de l'angle. Cela signifie que pour certaines valeurs du rapport d / λ , il a des maxima de diffraction (supplémentaires).
Diagramme d'antenne non normalisé pour N = 5
Diagramme de rayonnement normalisé du réseau d'antennes pour N = 5 dans le système de coordonnées polaires

La position des "diffractionnistes" peut être visualisée directement à partir de la formule du NAM. Cependant, nous allons essayer de comprendre d'où ils viennent physiquement et géométriquement (dans l'espace N-dimensionnel).

Les éléments du vecteur de phasage sont des exposants complexes$$ $ inline $ e ^ {i \ Psi n} $ inline $ dont les valeurs sont déterminées par la valeur de l'angle généralisé$$ $ inline $ \ Psi = 2 \ pi \ frac {d} {\ lambda} \ sin \ phi $ inline $ . S'il existe deux angles généralisés correspondant à différentes directions d'arrivée d'une onde plane, pour lesquels$$ $ inline $ \ Psi_1 = \ Psi_2 + 2 \ pi m $ inline $ , cela signifie deux choses:

• Physiquement: les fronts d'onde plans issus de ces directions induisent des distributions d'amplitude-phase identiques des ondes électromagnétiques sur les éléments du réseau d'antennes.
• Géométriquement: les vecteurs de phasage pour ces deux directions coïncident.

Les directions d'arrivée des ondes connectées de manière similaire sont équivalentes du point de vue du réseau d'antennes et ne se distinguent pas les unes des autres.

Comment déterminer la région d'angles dans laquelle se trouve toujours un seul maximum principal du MD ? Nous le ferons au voisinage de l'azimut nul pour les raisons suivantes: le déphasage entre deux éléments adjacents doit se situer dans l'intervalle de$$ $ inline $ - \ pi $ inline $ avant$$ $ inline $ \ pi $ inline $ .

$$$$ afficher $$ - \ pi <2 \ pi \ frac {d} {\ lambda} \ sin \ phi <\ pi $$ afficher $$

En résolvant cette inégalité, on obtient la condition sur la région d'unicité dans un voisinage de zéro:

$$$$ afficher $$ | \ sin \ phi | <\ frac {\ lambda} {2d} $$ afficher $$

On peut voir que la taille de la région d'unicité en angle dépend du rapport d / λ . Si d = 0,5 λ , alors chaque direction d'arrivée du signal est «individuelle» et la région d'unicité couvre toute la gamme des angles. Si d = 2,0 λ , alors les directions 0, ± 30, ± 90 sont équivalentes. Des lobes de diffraction apparaissent sur le diagramme de rayonnement.

En règle générale, les lobes de diffraction ont tendance à supprimer en utilisant des éléments d'antenne directionnelle. Dans ce cas, le diagramme de rayonnement complet du réseau d'antennes est le produit du diagramme d' un élément et du réseau d'éléments isotropes. Les paramètres DN d'un élément sont généralement sélectionnés en fonction de la condition sur la région d'unicité du réseau d'antennes.

La largeur du lobe principal

La formule d'ingénierie pour estimer la largeur du lobe principal du système d'antenne est largement connue :$$ $ inline $ \ Delta \ phi ≈ \ frac {\ lambda} {D} $ inline $ où D est la taille caractéristique de l'antenne. La formule est utilisée pour différents types d'antennes, y compris les SLR. Nous montrons qu'il est également valable pour les réseaux d'antennes.

Nous déterminons la largeur du lobe principal par les premiers zéros du MD au voisinage du maximum principal. Numérateur d' expression pour$$ $ inline $ F (\ phi) $ inline $ disparaît à$$ $ inline $ \ sin \ phi = m \ frac {\ lambda} {dN} $ inline $ . Les premiers zéros correspondent à m = ± 1. En supposant$$ $ inline $ \ frac {\ lambda} {dN} << 1 $ inline $ nous obtenons$$ $ inline $ \ Delta \ phi = 2 \ frac {\ lambda} {dN} $ inline $ .

Typiquement, la largeur du faisceau de directivité AR est déterminée par le demi-niveau de puissance (-3 dB). Dans ce cas, utilisez l'expression:

$$$$ afficher $$ \ Delta \ phi≈0.88 \ frac {\ lambda} {dN} $$ afficher $$

La largeur du lobe principal peut être contrôlée en définissant différentes valeurs des amplitudes pour les coefficients de poids du réseau d'antennes. Considérez trois distributions:

• Distribution d'amplitude uniforme (poids 1):$$ $ inline $ w_n = 1 $ inline $ .
• Valeurs d'amplitude tombant sur les bords du réseau (poids 2):$$ $ inline $ w_n = 0,5 + 0,3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ inline $
• Valeurs d'amplitude augmentant jusqu'aux bords du réseau (poids 3):$$ $ inline $ w_n = 0,5-0,3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ inline $

La figure montre les diagrammes de rayonnement normalisés résultants sur une échelle logarithmique:
Les tendances suivantes peuvent être tracées à partir de la figure: la distribution des amplitudes des coefficients de poids décroissant vers les bords du réseau conduit à un élargissement du lobe principal du MD, mais à une diminution du niveau des lobes latéraux. Les amplitudes croissantes vers les bords du réseau d'antennes conduisent au contraire à un rétrécissement du lobe principal et à une augmentation du niveau des côtés. Il est utile d'envisager de limiter les cas ici:

1. Les amplitudes des coefficients de pondération de tous les éléments sauf les extrêmes sont égales à zéro. Les poids des éléments extrêmes sont égaux à l'unité. Dans ce cas, le réseau devient équivalent à un AR à deux éléments avec une période de D = (N-1) d . Il n'est pas difficile d'estimer selon la formule ci-dessus la largeur du pétale principal. Dans ce cas, les latérales se transformeront en maxima de diffraction et s'aligneront sur le maximum principal.
2. Le poids de l'élément central est égal à un et tout le reste à zéro. Dans ce cas, nous avons essentiellement obtenu une antenne avec un diagramme de rayonnement isotrope.

La direction du maximum principal

Nous avons donc examiné comment ajuster la largeur du lobe principal de l' AP AR . Voyons maintenant comment diriger la direction. Rappelez l' expression vectorielle du signal reçu. Supposons que nous voulons que le diagramme de rayonnement maximal regarde dans une certaine direction$$ $ inline $ \ phi_0 $ inline $ . Cela signifie que la puissance maximale doit être prise dans cette direction. Le vecteur de phasage correspond à cette direction$$ $ inline $ \ textbf {s} (\ phi_0) $ inline $ dans l'espace vectoriel N- dimensionnel, et la puissance reçue est définie comme le carré du produit scalaire de ce vecteur de phasage par le vecteur des coefficients de pondération w . Le produit scalaire de deux vecteurs est maximal lorsqu'ils sont colinéaires , c'est-à-dire$$ $ inline $ \ textbf {w} = \ beta \ textbf {s} (\ phi_0) $ inline $ , où β est un facteur de normalisation. Ainsi, si nous choisissons un vecteur de poids égal au vecteur de phasage pour la direction souhaitée, alors nous tournerons le diagramme de rayonnement maximum.

Considérez les poids suivants comme exemple:$$ $ inline $ \ textbf {w} = \ textbf {s} (10 °) $ inline $

$$$$ afficher $$ w_n = \ exp \ {i2 \ pi \ frac {d} {\ lambda} (n-1) \ sin (10 \ pi / 180) \} $$ afficher $$

En conséquence, nous obtenons un diagramme de rayonnement avec le maximum principal dans la direction de 10 °.

Maintenant, nous appliquons les mêmes poids, mais pas pour la réception du signal, mais pour la transmission. Ici, il convient de considérer que lors de la transmission d'un signal, la direction du vecteur d'onde est inversée. Cela signifie que les éléments du vecteur de phasage pour la réception et la transmission diffèrent dans le signe de l'exposant, c'est-à-dire interconnectés par conjugaison complexe. Par conséquent, nous obtenons le maximum du diagramme de rayonnement dans la direction de -10 °, ce qui ne coïncide pas avec le maximum du signal de réception aux mêmes coefficients de poids. Pour corriger la situation, il est nécessaire d'appliquer également une conjugaison complexe aux coefficients de poids.

La caractéristique décrite de la formation des faisceaux pour la réception et la transmission doit toujours être gardée à l'esprit lorsque vous travaillez avec des réseaux d'antennes.

Jouons avec le diagramme de rayonnement

Quelques sommets

Nous posons le problème de former deux maximums principaux du diagramme de rayonnement dans la direction: -5 ° et 10 °. Pour ce faire, nous choisissons la somme pondérée des vecteurs de phasage pour les directions correspondantes comme vecteur de poids.

$$$$ afficher $$ \ textbf {w} = \ beta \ textbf {s} (10 °) + (1- \ beta) \ textbf {s} (- 5 °) $$ afficher $$

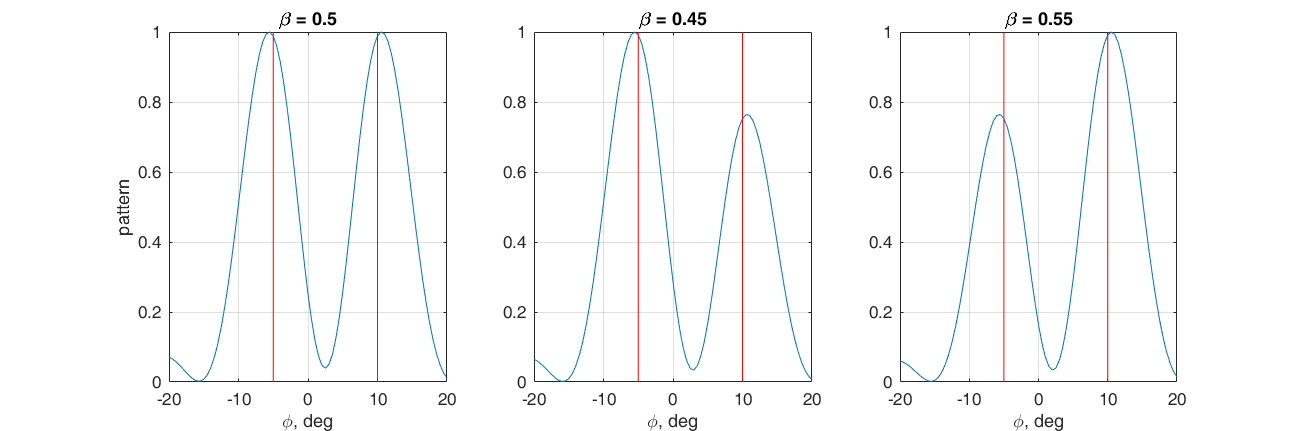
En ajustant le coefficient β , le rapport entre les lobes principaux peut être ajusté. Là encore, il est pratique de regarder ce qui se passe dans l'espace vectoriel. Si β est supérieur à 0,5, alors le vecteur de poids est plus proche de s (10 °), sinon de s (-5 °). Plus le vecteur de poids est proche de l'un des phaseurs, plus le produit scalaire correspondant est grand, et donc l'amplitude du maximum correspondant du ND .

Cependant, il convient de considérer que les deux pétales principaux ont une largeur finie, et si nous voulons syntoniser dans deux directions proches, ces pétales fusionneront en un seul, orienté dans une direction moyenne.

Un maximum et zéro

Essayons maintenant d'ajuster le diagramme de rayonnement maximal dans la direction$$ $ inline $ \ phi_1 = 10 ° $ inline $ et supprimer simultanément le signal provenant de la direction$$ $ inline $ \ phi_2 = -5 ° $ inline $ . Pour cela, il est nécessaire de régler le zéro pour l'angle correspondant. Vous pouvez le faire comme suit:

$$$$ afficher $$ \ textbf {w} = \ textbf {s} _1- \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {N} \ textbf {s} _2 $$ afficher $$

où$$ $ inline $ \ textbf {s} _1 = \ textbf {s} (10 °) $ inline $ et$$ $ inline $ \ textbf {s} _2 = \ textbf {s} (- 5 °) $ inline $ .

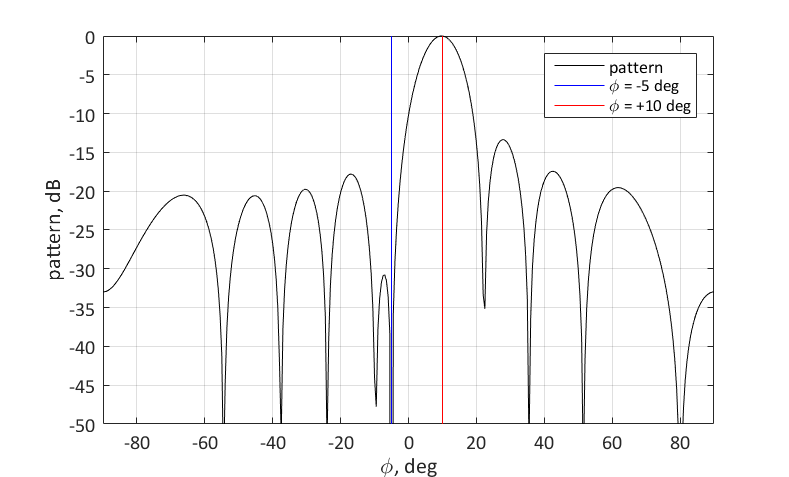
La signification géométrique du choix du vecteur de poids est la suivante. Nous voulons que ce vecteur w ait une projection maximale sur$$ $ inline $ \ textbf {s} _1 $ inline $ et était orthogonale au vecteur$$ $ inline $ \ textbf {s} _2 $ inline $ . Vecteur$$ $ inline $ \ textbf {s} _1 $ inline $ peut être représenté par deux termes: vecteur colinéaire$$ $ inline $ \ textbf {s} _2 $ inline $ et vecteur orthogonal$$ $ inline $ \ textbf {s} _2 $ inline $ . Pour satisfaire l'énoncé du problème, il est nécessaire de choisir la deuxième composante comme vecteur des coefficients de pondération w . La composante colinéaire peut être calculée en concevant un vecteur$$ $ inline $ \ textbf {s} _1 $ inline $ au vecteur normalisé$$ $ inline $ \ frac {\ textbf {s} _2} {\ sqrt {N}} $ inline $ en utilisant un produit scalaire.

$$$$ afficher $$ \ textbf {s} _ {1 ||} = \ frac {\ textbf {s} _2} {\ sqrt {N}} \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {\ sqrt {N}} $$ afficher $$

Par conséquent, soustraire du vecteur de phasage initial$$ $ inline $ \ textbf {s} _1 $ inline $ sa composante colinéaire, on obtient le vecteur poids souhaité.

Quelques notes supplémentaires

1. Partout ci-dessus, j'ai omis la question de la normalisation du vecteur de poids, c'est-à-dire sa longueur. Ainsi, la normalisation du vecteur de poids n'affecte pas les caractéristiques du diagramme de rayonnement du réseau d'antennes: la direction de la maxime principale, la largeur du lobe principal, etc. On peut également montrer que cette normalisation n'affecte pas le SNR en sortie du bloc de traitement spatial. À cet égard, lorsque j'envisage des algorithmes de traitement de signal spatial, j'accepte généralement une normalisation unitaire du vecteur de poids, c'est-à-dire$$ $ inline $ \ textbf {w} ^ H \ textbf {w} = 1 $ inline $
2. Les possibilités de formation du fond du réseau d'antennes sont déterminées par le nombre d'éléments N. Plus il y a d'éléments, plus les possibilités sont grandes. Plus il y a de degrés de liberté dans la mise en œuvre du traitement de poids spatial, plus il y a d'options pour "tordre" le vecteur de poids dans un espace à N dimensions.
3. Lors de la réception du diagramme de faisceau d' antenne , le réseau d'antennes n'existe pas physiquement, et tout cela n'existe que dans «l'imagination» de l'unité de calcul qui traite le signal. Cela signifie qu'en même temps, il est possible de synthétiser plusieurs MD et de traiter indépendamment les signaux provenant de directions différentes. Dans le cas de la transmission, tout est un peu plus compliqué, mais il est également possible de synthétiser plusieurs MD pour transmettre différents flux de données. Cette technologie dans les systèmes de communication est appelée MIMO .
4. En utilisant le code matlab fourni, vous pouvez jouer avec NAM vous-même
   
   Code

   % antenna array settings N = 10; % number of elements d = 0.5; % period of antenna array wLength = 1; % wavelength mode = 'receiver'; % receiver or transmitter % weights of antenna array w = ones(N,1); % w = 0.5 + 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = 0.5 - 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+10/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+3/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-3/180*pi)*(0:N-1)).'; % s1 = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % s2 = exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % w = s1 - (1/N)*s2*s2'*s1; % w = s1; % normalize weights w = w./sqrt(sum(abs(w).^2)); % set of angle values to calculate pattern angGrid_deg = (-90:0.5:90); % convert degree to radian angGrid = angGrid_deg * pi / 180; % calculate set of steerage vectors for angle grid switch (mode) case 'receiver' s = exp(2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); case 'transmitter' s = exp(-2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); end % calculate pattern y = (abs(w'*s)).^2; %linear scale plot(angGrid_deg,y/max(y)); grid on; xlim([-90 90]); % log scale % plot(angGrid_deg,10*log10(y/max(y))); % grid on; % xlim([-90 90]); 

   
   

Quelles tâches peuvent être résolues à l'aide d'un réseau d'antennes adaptatives?

Merci de votre attention.