Ceci est la traduction d'un article d'Eliezer Yudkovsky d'un cycle scientifique populaire consacré à l'interprétation multivariée de la mécanique quantique. Le début du cycle a été traduit en plaque tournante , mais le traducteur s'est apparemment fatigué. On le comprend - le matériau est très volumineux. Yudkovsky aime répandre la pensée sur l'arbre. D'un autre côté, le matériel est vraiment complexe, et la répétition de la même chose dans des mots différents permet à l'image dans la tête d'un lecteur non préparé de se maintenir au moins en quelque sorte. Je ne m'engagerai pas à poursuivre la traduction de l'ensemble du cycle, mais j'essaierai de traduire quelques-uns des articles les plus importants.

Je vais sauter des articles de la série sur les espaces d'états ( classiques et quantiques ) - le concept est beaucoup utilisé et devrait être familier à un lecteur techniquement formé. Et ignorez également les intégrales du chemin Feynman - elles peuvent être trouvées dans l'excellente source scientifique populaire.

Mais le prochain article répond à une question importante. Si le monde «réel» au niveau fondamental est quantique, où tout est confus et tout s’affecte, d’où viennent les systèmes classiques? Pourquoi voyons-nous si rarement des phénomènes quantiques «naturels» dans la vie ordinaire? C'est ce que l'auteur appelle «l'hallucination classique». Pourquoi, par exemple, les créateurs d'ordinateurs quantiques doivent-ils faire des efforts énormes pour maintenir le système dans un état intriqué "naturel"?

Avertissement: je ne suis ni un physicien professionnel ni un traducteur professionnel (ainsi que l'auteur de l'original).

Décohérence

Pour comprendre un processus quantique appelé «décohérence», vous devez d'abord comprendre comment un état spécial d'indépendance quantique est détruit - c'est-à-dire, comment exactement un système quantique passe d'un état d'indépendance à un état d'enchevêtrement.

L'indépendance quantique, comme nous le rappelons , est un état spécial, «rectangulaire» de distribution d'amplitude qui est bien factorisé. Autrement dit, il peut être représenté comme le produit des distributions des parties constitutives du système, qui pour nous ressemblent à des «particules séparées».

Les touristes timides visitant notre monde quantique prennent parfois l'absence d'une telle distribution «rectangulaire» pour une connexion mystérieuse spéciale entre les particules. D'où le malheureux terme «enchevêtrement quantique». En fait, toute évolution d'un système quantique génère généralement un enchevêtrement par rapport à l'indépendance (et non l'inverse), transformant des distributions rectangulaires en distributions non rectangulaires. L'indépendance est rare et très facile à détruire.

Pour mieux comprendre exactement quels processus physiques conduisent à l'intrication, nous commençons par le système classique. La figure montre un système d'une balle légère chargée positivement sur la piste supérieure et d'une balle lourde chargée négativement sur la piste inférieure. Au départ, deux balles sont éloignées l'une de l'autre et n'interagissent presque pas. Ensuite, nous abaissons le chemin supérieur, en rapprochant les boules pour qu'elles commencent à s'attirer (les charges opposées sont attirées). Et une boule légère roule jusqu'à une lourde (et une boule lourde roule un peu à une légère, tout comme une pomme qui tombe attire légèrement la Terre sur elle-même).

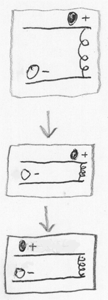
Voyons maintenant ce système comme un système quantique, du point de vue des intégrales de chemin de Feynman . Autrement dit, nous représentons l'évolution du système comme la somme de toutes les trajectoires possibles à partir de l'état initial dans l'espace de configuration. Supposons que deux boules soient initialement indépendantes quantiquement, leur distribution conjointe d'amplitudes peut être représentée comme le produit de «distribution pour la balle inférieure» et «distribution pour la balle supérieure».

De plus, que l'amplitude de la balle inférieure au début se compose de trois parties (qui du point de vue des intégrales de Feynman peuvent être considérées comme trois états initiaux). Lorsque nous abaissons la piste supérieure, la balle supérieure doit être tirée vers la piste inférieure. Mais si l'amplitude articulaire de la balle inférieure se compose de plusieurs parties, nous obtiendrons finalement une distribution conjointe composée de plusieurs parties, chacune décrivant la nouvelle position des billes.

Je fais de mon mieux pour éviter les formulations telles que «la balle inférieure peut être à l'un des trois endroits» ou «dans chaque cas possible, la balle supérieure est attirée vers la position correspondante de la balle inférieure». Bien que vous imaginiez probablement toujours tout de cette façon. Au final, je l'ai moi-même illustré. J'ai dessiné trois positions de départ possibles et trois résultats possibles. Que faire, le cerveau humain imagine généralement des intégrales de Feynman. Mais cela ne signifie pas qu'il existe trois états possibles de l'univers . C'est juste une astuce pour visualiser l'intégrale du chemin. Les trois composantes de l'amplitude existent dans notre univers, les trois sont également réelles , mais pas du tout possibles ou probables .

Imaginez maintenant qu'au début, l'amplitude de la balle inférieure soit «étalée» sur toute la piste. L'amplitude de la balle supérieure est toujours concentrée en un seul endroit. Ensuite, la distribution conjointe sera initialement sous la forme d'un rectangle allongé, puis se transformera en diagonale.

Sur l'axe X, voici la position de la balle supérieure, sur l'axe Y - le bas. Nous commençons avec une balle supérieure localisée avec précision et une balle inférieure «floue» et nous terminons avec une distribution interdépendante lorsque les deux coordonnées sont floues mais égales l'une à l'autre (simplifiées). C'est-à-dire que la distribution initialement factorisable s'est transformée en un "système déroutant" - elle ne se décompose plus en deux facteurs indépendants.

(Avis important:

Notez que dans la figure ci-dessus, le développement du système obéit à la deuxième loi de la thermodynamique , alias le théorème de Liouville. Lorsque le système change, la «taille du nuage» est préservée, c'est-à-dire le volume total de l'amplitude, ou plus simplement, la taille de la zone grise sur le graphique . Si au début de la figure il y avait un énorme carré gris clair (lorsque les deux particules sont fortement maculées dans l'espace), alors selon la deuxième loi de la thermodynamique, il ne pourrait pas se transformer en une diagonale gris foncé. Pour entrer dans un état d'enchevêtrement, le système devrait initialement avoir une faible entropie, et cette entropie ne devrait pas augmenter beaucoup dans le processus.

Permettez-moi de vous rappeler que l'information mutuelle est entropiée avec le signe opposé . Les amplitudes quantiques ne sont pas entièrement informationnelles , mais le principe est le même. L'amplitude initiale doit être suffisamment concentrée pour produire une ligne diagonale compacte, au lieu d'un gros nuage raréfié. Si nous imaginons que la distribution d'amplitude a une «entropie quantique», alors l'entropie du système enchevêtré devrait être relativement faible)

Enfin, nous sommes prêts à parler de décohérence.

Le système de la figure est assez compliqué. On peut décrire quelque chose comme ceci: "il y a deux particules, et les deux peuvent être ici ou là ". Oui, je l'ai formulé comme s'il y avait deux états possibles, et non une distribution physiquement réelle de l'amplitude. Sérieusement, je ne sais pas comment décrire la physique quantique dans un langage ordinaire d'une manière normale! N'oubliez pas la règle générale selon laquelle «opportunité» ou «probabilité» est l'abréviation de «étirement de distribution d'amplitude existant physiquement». Ensuite, je peux décrire les amplitudes beaucoup plus courtes en utilisant les termes d'incertitudes. Mais rappelez-vous que ce n'est qu'une convention ! «Une particule est ici ou là» signifie «une distribution physiquement existante de l'amplitude de deux parties, une ici, une là», et non «la particule est à l'un des deux endroits, mais nous ne savons pas laquelle».

Alors. Travailler avec des systèmes complexes est généralement difficile (pour les physiciens, bien sûr, pas pour l'univers). Premièrement, nous devons calculer toutes les trajectoires possibles pour toutes les conditions initiales possibles (c'est-à-dire prendre en compte toutes les trajectoires d'amplitude physiquement existantes dans l'intégrale de Feynman). De plus, il est nécessaire de prendre en compte l'influence de ces trajectoires les unes sur les autres (les trajectoires probables au sens strict ne peuvent pas interagir - seul quelque chose de réellement existant peut influencer autre chose). Par exemple, nos deux particules rencontrent 20 autres, interagissent d'une manière ou d'une autre, et en conséquence nous obtenons un tas de configurations qui ont été affectées par tous les points précédents de tous les états possibles.

Notez que l'intrication ne se produit que si les sections de l'amplitude initiale sont proches les unes des autres. Pour que leurs voies de développement puissent se croiser. Si deux particules sont ici ou là , mais "ici" et "là" sont séparés par une distance de deux années-lumière, alors leurs trajectoires supplémentaires peuvent se croiser au plus tôt un an plus tard.

Ajoutez maintenant la troisième particule. La figure montre un espace de configuration en trois dimensions, qui se décompose en sous-espaces bidimensionnels et unidimensionnels indépendants. Autrement dit, deux particules enchevêtrées et une indépendante d'entre elles.

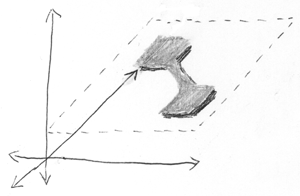
La hauteur est la troisième particule, la largeur et la profondeur sont deux particules enchevêtrées.

Une particule indépendante est à un certain endroit - la distribution verticale est très étroite. Deux particules enchevêtrées sont ici ou là (j'utilise encore des termes probabilistes incorrects, tels que «spécifique» et «non plus», mais vous comprenez ce que je veux dire).

Imaginez maintenant que la troisième particule réagit avec les deux enchevêtrés d'une manière qui est sensible à leur position. Par exemple, la troisième particule s'équilibre sur un pic pointu, deux particules survolent, l'attirent et elles tombent dans un sens ou dans l'autre. Après cela, l'amplitude ressemble à ceci.

La troisième particule est maintenant confondue avec les deux autres. Et l'amplitude se compose désormais de deux pièces séparées l'une de l'autre . Description simplifiée: «si deux particules étaient ici , alors la troisième particule a volé ici . Et s'ils étaient là , alors elle a pris l'avion. » Autrement dit, l'amplitude est devenue complètement confuse. Il ne se décompose plus en sous-espaces indépendants.

Mais deux morceaux d'amplitude sont maintenant plus éloignés l'un de l'autre , et chacun se compose de trois particules dans la région correspondante. Cela s'est produit parce que la troisième particule est sensible aux coordonnées des autres. Après avoir roulé d'un pic pointu vers l'un des deux côtés, la distance entre les coordonnées finales est assez grande.

En fait, la descente par le haut est facultative. Tout fonctionne de la même manière si vous avez vingt particules qui réagissent aux deux premières et se confondent avec elles. La distribution finale dans l'espace à 22 dimensions ressemblera à deux zones, chacune correspondant à 22 particules. Et la distance entre ces zones sera énorme. Et plus la distance est grande, moins il est probable que des zones futures se toucheront mutuellement.
C'est la décohérence. C'est la troisième cause de «l'hallucination classique», car les deux zones commencent à se développer indépendamment. Cela leur permet d'être décrits comme des systèmes non complexes. Dès que nous les considérons séparément, la distribution dans chacun d'eux semble «rectangulaire» et indépendante en trois coordonnées (j'ai essayé de le montrer dans la figure ci-dessus).

Dans un ordinateur quantique, il est très difficile d' empêcher la décohérence. L'informatique quantique nécessite que les sections d'amplitude restent proches les unes des autres et puissent interagir. Mais il y a des milliards d'autres particules autour qui essaient constamment de réagir par inadvertance avec nos qubits fragiles, détruisant une amplitude précisément construite.

Et vous ne pouvez pas simplement prendre et restaurer les détruits. Pour ce faire, il faut ramener à l'endroit toutes les particules ayant réagi, y compris les particules aléatoires de l'environnement (n'oubliez pas, l'amplitude finale a une distribution conjointe avec elles).

(Cela ressemble à un processus presque irréversible, non? C'est comme essayer de récupérer un œuf cassé dans la coquille. En fait, c'est une bonne analogie.

C'est pourquoi j'ai souligné plus tôt que le processus d'enchevêtrement commence par une faible entropie. La décohérence est irréversible car il s'agit essentiellement d'un processus thermodynamique.

L'un des principes physiques fondamentaux stipule que vous pouvez "faire reculer le film" sans violer les lois fondamentales. Si vous filmez un œuf qui tombe sur le sol, puis faites-le rouler vers l'arrière, de sorte qu'un œuf cassé vole du sol et se rassemble dans une coquille lisse, vous ne verrez aucune loi physique violée. Toutes les molécules seront simplement au bon endroit au bon moment et l'œuf rebondira sain et sauf sur le sol. Ce n'est pas impossible, juste extrêmement improbable.

La même chose s'applique à l'amplitude divisée en morceaux éloignés, revenant de façon inattendue à un état cohérent - c'est théoriquement possible. Mais il n'y a pratiquement aucune chance que les pièces initialement déconnectées se retrouvent soudainement simultanément les unes à côté des autres. Le processus inverse est beaucoup plus probable.

En fait, en plus de faire défiler le film en arrière, vous devez également inverser les charges de toutes les particules, ainsi qu'échanger la gauche et la droite (ou l'une des deux autres dimensions), transformant l'univers en une image miroir de celui-ci. Cette règle est connue sous le nom d '«invariance CPT» à partir des mots Charge, Parité et Temps.

L'invariance CPT est très probablement l'un des principes les plus fondamentaux du fonctionnement de l'univers. Pour les physiciens, les tentatives de le casser semblent presque aussi absurdes que d'essayer de lancer une balle plus vite que la vitesse de la lumière. Pour autant que je sache, l'invariance CPT est nécessaire pour la cohérence de la théorie quantique des champs.

Par conséquent, la décohérence ne ressemble qu'à un processus unidirectionnel, mais en fait son irréversibilité est thermodynamique, pas fondamentale. Et cela est très important, car il en résulte que la physique quantique observe l'invariance CPT.

À notre connaissance, absolument tous les processus unidirectionnels dans la nature sont la conséquence de la deuxième loi de la thermodynamique, et non de l'asymétrie fondamentale du temps.)

Pour résumer. La décohérence est un processus thermodynamique d'un enchevêtrement quantique sans cesse croissant, qui est étonnamment déguisé en un processus de destruction de cet enchevêtrement lui-même. Les zones décohérentes n'interagissent pas les unes avec les autres et chacune d'entre elles devient moins déroutante . La décohérence est la troisième raison de "l'hallucination classique". Il permet aux physiciens de considérer chaque champ comme indépendant, sans tenir compte de la faible probabilité de leur interaction. De plus, chaque domaine individuel devient plus facile à comprendre à l' intérieur . Ceci est très utile si vous souhaitez résoudre des problèmes en termes de physique classique simple. Et il est très inapproprié de prendre en compte un million de chiffres avant le coucher du soleil.