Bonjour mes amis. Le cours
Algorithms for Developers commence demain, et nous avons encore une traduction non publiée. En fait, nous corrigeons et partageons le matériel avec vous. Allons-y.
La transformation de Fourier rapide (FFT) est l'un des algorithmes les plus importants de traitement du signal et d'analyse de données. Je l'ai utilisé pendant des années sans connaissances formelles en informatique. Mais cette semaine, il m'est venu à l'esprit que je ne me suis jamais demandé comment la FFT calcule la transformée de Fourier discrète si rapidement. J'ai secoué la poussière d'un vieux livre sur les algorithmes, l'ai ouvert et j'ai lu avec plaisir l'astuce de calcul trompeusement simple que J.V.Cooley et John Tukey ont décrite dans leur
ouvrage classique de
1965 sur ce sujet.
Le but de ce post est de plonger dans l'algorithme FFT de Cooley-Tukey, expliquant les symétries qui y conduisent, et de montrer quelques implémentations Python simples qui appliquent la théorie dans la pratique. J'espère que cette étude donnera aux spécialistes de l'analyse des données, comme moi, une image plus complète de ce qui se passe sous le capot des algorithmes que nous utilisons.
Transformation de Fourier discrèteLa FFT est rapide
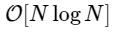
un algorithme de calcul de la transformée de Fourier discrète (DFT), qui est directement calculé pour
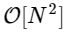
. La DFT, comme la version continue plus familière de la transformée de Fourier, a une forme directe et inverse, qui sont définies comme suit:
Transformation de Fourier discrète directe (DFT):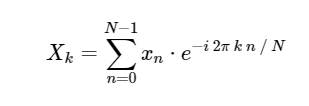
Transformée de Fourier discrète inverse (ODPF):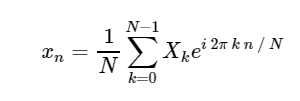
La conversion de
xn → Xk est une traduction de l'espace de configuration vers l'espace de fréquence et peut être très utile à la fois pour étudier le spectre de puissance du signal et pour convertir certaines tâches pour un calcul plus efficace. Vous pouvez trouver quelques exemples de cela en action dans le
chapitre 10 de notre futur livre sur l'astronomie et les statistiques, où vous pouvez également trouver des images et du code source Python. Pour un exemple d'utilisation de la FFT pour simplifier l'intégration d'équations différentielles autrement compliquées, voir mon article
«Résoudre l'équation de Schrödinger en Python» .
En raison de l'importance de la FFT (ci-après, l'équivalent FFT - Fast Fourier Transform peut être utilisé) dans de nombreux domaines de Python contient de nombreux outils et shells standard pour le calculer. NumPy et SciPy ont tous les deux des shells de la bibliothèque FFTPACK extrêmement bien testée, qui sont situés dans les
scipy.fftpack numpy.fft et
scipy.fftpack respectivement. La FFT la plus rapide que je connaisse se trouve dans le package
FFTW , qui est également disponible en Python via le package
PyFFTW .
Pour le moment, cependant, laissons ces implémentations de côté et nous demandons comment nous pouvons calculer la FFT en Python à partir de zéro.
Calcul de transformée de Fourier discrètePar souci de simplicité, nous ne traiterons que de la conversion directe, car la transformation inverse peut être implémentée de manière très similaire. En regardant l'expression ci-dessus de la DFT, nous voyons que ce n'est rien de plus qu'une opération linéaire simple: multiplier la matrice par un vecteur
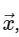
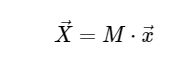
avec matrice M donnée
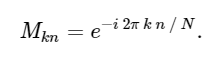
Dans cet esprit, nous pouvons calculer la DFT en utilisant une simple multiplication matricielle comme suit:
Dans [1]:
import numpy as np def DFT_slow(x): """Compute the discrete Fourier Transform of the 1D array x""" x = np.asarray(x, dtype=float) N = x.shape[0] n = np.arange(N) k = n.reshape((N, 1)) M = np.exp(-2j * np.pi * k * n / N) return np.dot(M, x)
Nous pouvons revérifier le résultat en le comparant avec la fonction FFT intégrée à numpy:
Dans [2]:
x = np.random.random(1024) np.allclose(DFT_slow(x), np.fft.fft(x))
0ut [2]:
TrueJuste pour confirmer la lenteur de notre algorithme, nous pouvons comparer le temps d'exécution de ces deux approches:
Dans [3]:
%timeit DFT_slow(x) %timeit np.fft.fft(x)
10 loops, best of 3: 75.4 ms per loop 10000 loops, best of 3: 25.5 µs per loop
Nous sommes plus de 1000 fois plus lents, ce qui est à prévoir pour une telle implémentation simplifiée. Mais ce n'est pas le pire. Pour un vecteur d'entrée de longueur N, l'algorithme FFT évolue comme
tandis que notre algorithme lent évolue comme
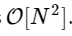
. Cela signifie que pour
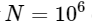
éléments, nous nous attendons à ce que la FFT se termine dans environ 50 ms, tandis que notre algorithme lent prendra environ 20 heures!
Alors, comment la FFT parvient-elle à une telle accélération? La réponse est d'utiliser la symétrie.
Symétries dans la transformée de Fourier discrèteL'un des outils les plus importants dans la construction d'algorithmes est l'utilisation de symétries de tâches. Si vous pouvez montrer analytiquement qu'une partie du problème est simplement liée à l'autre, vous ne pouvez calculer le sous-résultat qu'une seule fois et enregistrer ce coût de calcul. Cooley et Tukey ont utilisé exactement cette approche pour obtenir la FFT.
Nous commençons par la question du sens
. De notre expression ci-dessus:
où nous avons utilisé l'identité exp [2π in] = 1, qui vaut pour tout entier n.
La dernière ligne montre bien la propriété de symétrie de la DFT:
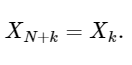
Une extension simple
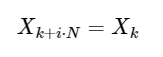
pour tout entier i. Comme nous le verrons ci-dessous, cette symétrie peut être utilisée pour calculer la DFT beaucoup plus rapidement.
DFT dans FFT: utiliser la symétrieCooley et Tukey ont montré que les calculs FFT peuvent être divisés en deux parties plus petites. D'après la définition de DFT, nous avons:
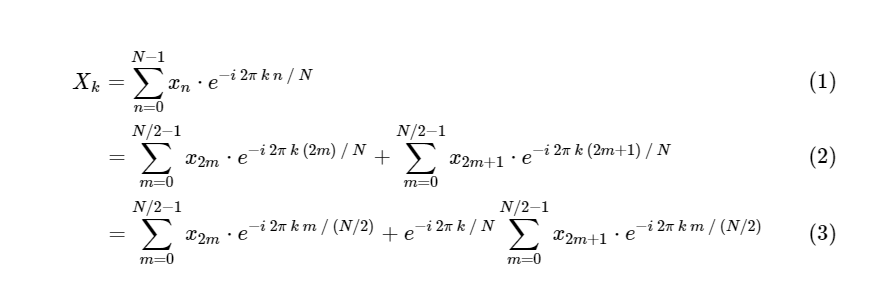
Nous avons divisé une transformée de Fourier discrète en deux termes, qui en eux-mêmes sont très similaires aux petites transformées de Fourier discrètes, une aux valeurs avec un nombre impair et une aux valeurs avec un nombre pair. Cependant, jusqu'à présent, nous n'avons enregistré aucun cycle de calcul. Chaque terme se compose de (N / 2) ∗ N calculs, total
.
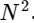
L'astuce consiste à utiliser la symétrie dans chacune de ces conditions. Puisque la plage de k est 0≤k <N, et la plage de n est 0≤n <M≡N / 2, nous voyons dans les propriétés de symétrie ci-dessus que nous devons effectuer seulement la moitié des calculs pour chaque sous-tâche. Notre calcul
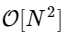
est devenu
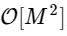
où M est deux fois moins que N.
Mais il n'y a aucune raison de s'y attarder: tant que nos petites transformées de Fourier ont un M pair, nous pouvons réappliquer cette approche diviser pour mieux régner, en réduisant chaque fois de moitié le coût de calcul, jusqu'à ce que nos matrices soient suffisamment petites pour que la stratégie ne profite plus. Dans la limite asymptotique, cette approche récursive évolue comme O [NlogN].
Cet algorithme récursif peut être implémenté très rapidement en Python, à partir de notre code DFT lent, lorsque la taille de la sous-tâche devient assez petite:
Dans [4]:
def FFT(x): """A recursive implementation of the 1D Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if N % 2 > 0: raise ValueError("size of x must be a power of 2") elif N <= 32:
Ici, nous allons vérifier rapidement que notre algorithme donne le résultat correct:
Dans [5]:
x = np.random.random(1024) np.allclose(FFT(x), np.fft.fft(x))
Sortie [5]:
TrueComparez cet algorithme avec notre version lente:
-Dans [6]:
%timeit DFT_slow(x) %timeit FFT(x) %timeit np.fft.fft(x)
10 loops, best of 3: 77.6 ms per loop 100 loops, best of 3: 4.07 ms per loop 10000 loops, best of 3: 24.7 µs per loop
Notre calcul est plus rapide que la version directe! De plus, notre algorithme récursif est asymptotiquement
: nous avons implémenté la transformée de Fourier rapide.
Notez que nous ne sommes toujours pas proches de la vitesse de l'algorithme FFT intégré numpy, et cela devrait être prévu. L'algorithme FFTPACK derrière
fft numpy est une implémentation Fortran qui a reçu des années de raffinement et d'optimisation. De plus, notre solution NumPy inclut à la fois la récursivité de la pile Python et l'allocation de nombreux tableaux temporaires, ce qui augmente le temps de calcul.
Une bonne stratégie pour accélérer le code lorsque vous travaillez avec Python / NumPy consiste à vectoriser les calculs répétitifs autant que possible. Nous pouvons le faire - dans le processus, supprimez nos appels de fonction récursifs, ce qui rendra notre FFT Python encore plus efficace.
Version Numpy vectoriséeVeuillez noter que dans l'implémentation récursive de la FFT ci-dessus, au niveau de récursivité le plus bas, nous effectuons
N / 32 produits matriciels vectoriels identiques. L'efficacité de notre algorithme gagnera si nous calculons simultanément ces produits matriciels-vectoriels comme un seul produit matriciel-matrice. À chaque niveau de récursivité suivant, nous effectuons également des opérations répétitives qui peuvent être vectorisées. NumPy fait un excellent travail d'une telle opération, et nous pouvons utiliser ce fait pour créer cette version vectorisée de la transformée de Fourier rapide:
Dans [7]:
def FFT_vectorized(x): """A vectorized, non-recursive version of the Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if np.log2(N) % 1 > 0: raise ValueError("size of x must be a power of 2")
Bien que l'algorithme soit légèrement plus opaque, il s'agit simplement d'un réarrangement des opérations utilisées dans la version récursive, à une exception près: nous utilisons la symétrie dans le calcul des coefficients et ne construisons que la moitié du tableau. Encore une fois, nous confirmons que notre fonction donne le résultat correct:
Dans [8]:
x = np.random.random(1024) np.allclose(FFT_vectorized(x), np.fft.fft(x))
Sortie [8]:
TrueComme nos algorithmes deviennent beaucoup plus efficaces, nous pouvons utiliser un tableau plus grand pour comparer le temps, laissant
DFT_slow :
Dans [9]:
x = np.random.random(1024 * 16) %timeit FFT(x) %timeit FFT_vectorized(x) %timeit np.fft.fft(x)
10 loops, best of 3: 72.8 ms per loop 100 loops, best of 3: 4.11 ms per loop 1000 loops, best of 3: 505 µs per loop
Nous avons amélioré notre mise en œuvre d'un ordre de grandeur! Nous sommes maintenant à environ 10 fois loin du benchmark FFTPACK, en utilisant seulement quelques dizaines de lignes de Python + NumPy pur. Bien que cela ne soit toujours pas cohérent sur le plan des calculs, en termes de lisibilité, la version Python est de loin supérieure au code source FFTPACK, que vous pouvez consulter
ici .
Alors, comment FFTPACK parvient-il à cette dernière accélération? Eh bien, fondamentalement, c'est juste une question de comptabilité détaillée. FFTPACK passe beaucoup de temps à réutiliser tous les calculs intermédiaires qui peuvent être réutilisés. Notre version irrégulière inclut toujours l'allocation et la copie de mémoire en excès; dans un langage de bas niveau tel que Fortran, il est plus facile de contrôler et de minimiser l'utilisation de la mémoire. De plus, l'algorithme Cooley-Tukey peut être étendu pour utiliser des partitions d'une taille autre que 2 (ce que nous avons mis en œuvre ici est connu sous le nom de Cooley-Tukey Radix FFT à partir de la base 2). D'autres algorithmes FFT plus complexes peuvent également être utilisés, y compris des approches fondamentalement différentes basées sur des données de convolution (voir, par exemple, l'algorithme Blueshtein et l'algorithme Raider). La combinaison des extensions et des méthodes ci-dessus peut conduire à des FFT très rapides même sur des tableaux dont la taille n'est pas une puissance de deux.
Bien que les fonctions en Python pur soient probablement inutiles dans la pratique, j'espère qu'elles fournissent un aperçu de ce qui se passe dans le contexte de l'analyse des données basée sur FFT. En tant que spécialistes des données, nous pouvons faire face à la mise en œuvre de la «boîte noire» des outils fondamentaux créés par nos collègues plus algorithmiques, mais je crois fermement que plus nous comprenons les algorithmes de bas niveau que nous appliquons à nos données, les meilleures pratiques nous le ferons.
Ce message a été entièrement écrit dans le bloc-notes IPython. Le bloc-notes complet peut être téléchargé
ici ou affiché statiquement
ici .
Beaucoup peuvent remarquer que le matériel n'est pas nouveau, mais, comme il nous semble, est tout à fait pertinent. En général, indiquez si l'article était utile. En attente de vos commentaires.