La vérification formelle est la vérification d'un programme ou d'un algorithme à l'aide d'un autre.
C'est l'une des méthodes les plus puissantes qui vous permet de trouver toutes les vulnérabilités dans le programme ou de prouver qu'elles ne sont pas là.
Une description plus détaillée de la vérification formelle peut être vue sur l'exemple de la résolution du problème du
loup, de la chèvre et du chou dans mon article précédent.
Dans cet article, je passerai de la vérification formelle des tâches aux programmes, et je décrirai
comment les convertir automatiquement en systèmes de règles formels.
Pour cela, j'ai écrit mon analogue d'une machine virtuelle, sur des principes symboliques.
Elle analyse le code du programme et le traduit en un système d'équations (SMT), qui peut déjà être résolu par programme.
Étant donné que les informations sur les calculs symboliques sont présentées de manière assez fragmentaire sur Internet,
Je vais décrire brièvement ce que c'est.
Les calculs de caractères sont un moyen d'exécuter simultanément un programme sur un large éventail de données et sont le principal outil de vérification formelle des programmes.
Par exemple, nous pouvons définir les conditions d'entrée où le premier argument peut prendre n'importe quelle valeur positive, le deuxième négatif, le troisième - zéro et l'argument de sortie, par exemple, 42.
Les calculs symboliques en une seule fois nous donneront la réponse, est-il possible pour nous d'obtenir le résultat souhaité et un exemple d'un ensemble de tels paramètres d'entrée. Ou la preuve qu'il n'y a pas de tels paramètres.
De plus, nous pouvons définir les arguments d'entrée en général comme possible, et sélectionner uniquement la sortie, par exemple, le mot de passe administrateur.
Dans ce cas, nous trouverons toutes les vulnérabilités du programme ou nous obtiendrons la preuve que le mot de passe administrateur est sûr.
Vous remarquerez peut-être que l'exécution classique d'un programme avec des données d'entrée spécifiques est un cas particulier de programme symbolique.
Par conséquent, ma machine virtuelle de personnage peut également fonctionner en mode d'émulation d'une machine virtuelle standard.
Dans les commentaires de l'article précédent, vous pouvez trouver une critique juste de la vérification formelle avec une discussion de ses faiblesses.
Les principaux problèmes sont les suivants:
- Explosion combinatoire, car la vérification formelle repose finalement sur P = NP
- La gestion des appels vers le système de fichiers, les réseaux et tout autre stockage externe est plus difficile à vérifier
- Bogues dans la spécification, lorsque le client ou le programmeur a conçu une chose, mais ne l'a pas décrite avec précision dans l'énoncé des travaux.
En conséquence, le programme sera vérifié et conforme aux spécifications, mais il ne fera pas du tout ce que les créateurs attendaient de lui.
Étant donné que dans cet article, je considère principalement l'application de la vérification formelle dans la pratique, je ne frapperai pas encore mon front contre le mur et je choisirai un système où la complexité algorithmique et le nombre d'appels externes sont minimes.
Étant donné que les contrats intelligents répondent au mieux à ces exigences, le choix s'est porté sur les contrats RIDE de la plate-forme Waves: ils ne sont pas complets de Turing et leur complexité maximale est artificiellement limitée.
Mais nous les considérerons uniquement du côté technique.
De plus, pour tout contrat, une vérification formelle sera particulièrement demandée: en règle générale, il est impossible de corriger une erreur de contrat après son lancement.
Et le prix de ces erreurs peut être très élevé, car des sommes assez importantes sont souvent stockées dans des contrats intelligents.
Ma machine virtuelle de personnage est écrite en PHP et Python et utilise le Z3Prover de Microsoft Research pour résoudre les formules SMT résultantes.
À sa base se trouve une puissante recherche multi-transactionnelle, qui
vous permet de trouver des solutions ou des vulnérabilités, même si cela nécessite beaucoup de transactions.
Même
Mythril , l'un des cadres symboliques les plus puissants pour rechercher les vulnérabilités d'Ethereum, a ajouté cette fonctionnalité il y a seulement quelques mois.
Mais il convient de noter que les contrats d'éther sont plus complexes et ont l'intégralité de Turing.
PHP traduit le code source du contrat intelligent RIDE en un script python dans lequel le programme est présenté sous la forme d'un système de conditions contractuelles et de conditions pour leurs transitions compatibles avec Z3 SMT:
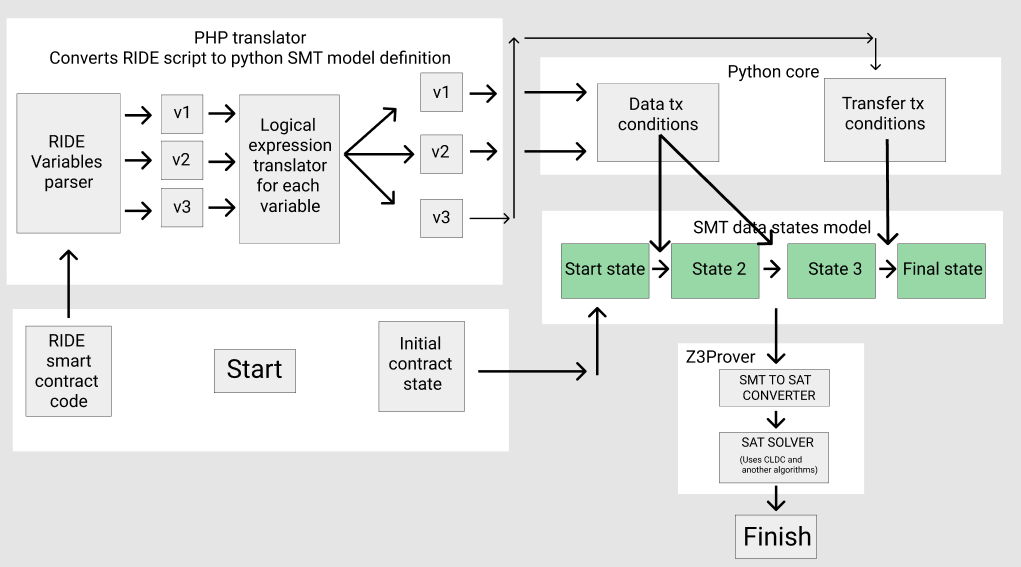
Je vais maintenant décrire plus en détail ce qui se passe à l'intérieur.
Mais d'abord, quelques mots sur le langage des contrats intelligents RIDE.
C'est un langage de programmation fonctionnel et basé sur l'expression qui est paresseux comme prévu.
RIDE est effectué de manière isolée au sein de la blockchain, et peut extraire et écrire des informations à partir du stockage associé au portefeuille de l'utilisateur.
Vous pouvez attacher un contrat RIDE à chaque portefeuille et le résultat de l'exécution ne sera que VRAI ou FAUX.
VRAI signifie que le contrat intelligent autorise la transaction et FAUX qu'il l'interdit.
Un exemple simple: un script peut interdire un transfert si le solde du portefeuille est inférieur à 100.
À titre d'exemple, je prendrai tout de même le loup, la chèvre et le chou, mais déjà présenté sous la forme d'un contrat intelligent.
L'utilisateur ne sera pas en mesure de retirer de l'argent du portefeuille sur lequel le contrat est déployé jusqu'à ce qu'il transfère tout le monde à l'autre côté.
# let contract = tx.sender let human= extract(getInteger(contract,"human")) let wolf= extract(getInteger(contract,"wolf")) let goat= extract(getInteger(contract,"goat")) let cabbage= extract(getInteger(contract,"cabbage")) # -, 4 . # . match tx { case t:DataTransaction => # let newHuman= extract(getInteger(t.data,"human")) let newWolf= extract(getInteger(t.data,"wolf")) let newGoat= extract(getInteger(t.data,"goat")) let newCabbage= extract(getInteger(t.data,"cabbage")) #0 , , 1 let humanSide= human == 0 || human == 1 let wolfSide= wolf == 0 || wolf == 1 let goatSide= goat == 0 || goat == 1 let cabbageSide= cabbage == 0 || cabbage == 1 let side= humanSide && wolfSide && goatSide && cabbageSide # , . let safeAlone= newGoat != newWolf && newGoat != newCabbage let safe= safeAlone || newGoat == newHuman let humanTravel= human != newHuman # , - . let t1= humanTravel && newWolf == wolf + 1 && newGoat == goat && newCabbage == cabbage let t2= humanTravel && newWolf == wolf && newGoat == goat + 1 && newCabbage == cabbage let t3= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage + 1 let t4= humanTravel && newWolf == wolf - 1 && newGoat == goat && newCabbage == cabbage let t5= humanTravel && newWolf == wolf && newGoat == goat - 1 && newCabbage == cabbage let t6= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage - 1 let t7= humanTravel && newWolf == wolf && newGoat == goat && newCabbage == cabbage let objectTravel = t1 || t2 || t3 || t4 || t5 || t6 || t7 # . # 1 0, # , # - side && safe && humanTravel && objectTravel case s:TransferTransaction => # human == 1 && wolf == 1 && goat == 1 && cabbage == 1 # case _ => false }
PHP extrait tout d'abord du smart contract toutes les variables sous forme de leurs clés et la variable correspondante de l'expression logique.
cabbage: extract ( getInteger ( contract , "cabbage" ) ) goat: extract ( getInteger ( contract , "goat" ) ) human: extract ( getInteger ( contract , "human" ) ) wolf: extract ( getInteger ( contract , "wolf" ) ) fState: human== 1 && wolf== 1 && goat== 1 && cabbage== 1 fState: wolf: goat: cabbage: cabbageSide: cabbage== 0 || cabbage== 1 human: extract ( getInteger ( contract , "human" ) ) newGoat: extract ( getInteger ( t.data , "goat" ) ) newHuman: extract ( getInteger ( t.data , "human" ) ) goatSide: goat== 0 || goat== 1 humanSide: human== 0 || human== 1 t7: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage t3: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage + 1 t6: humanTravel && newWolf== wolf && newGoat== goat && newCabbage== cabbage - 1 t2: humanTravel && newWolf== wolf && newGoat== goat + 1 && newCabbage== cabbage t5: humanTravel && newWolf== wolf && newGoat== goat - 1 && newCabbage== cabbage t1: humanTravel && newWolf== wolf + 1 && newGoat== goat && newCabbage== cabbage t4: humanTravel && newWolf== wolf - 1 && newGoat== goat && newCabbage== cabbage safeAlone: newGoat != newWolf && newGoat != newCabbage wolfSide: wolf== 0 || wolf== 1 humanTravel: human != newHuman side: humanSide && wolfSide && goatSide && cabbageSide safe: safeAlone || newGoat== newHuman objectTravel: t1 || t2 || t3 || t4 || t5 || t6 || t7
PHP les convertit ensuite en une description de système Python compatible pour Z3Prover SMT.
Les données sont encapsulées dans un cycle où les variables de stockage obtiennent l'index i, les variables de transaction l'index i + 1 et les variables avec des expressions définissent les règles pour la transition de l'état précédent au suivant.
C'est le cœur même de notre machine virtuelle, qui fournit un moteur de recherche multi-transactionnel.
fState: And( And( And( human[Steps] == 1 , wolf[Steps] == 1 ) , goat[Steps] == 1 ) , cabbage[Steps] == 1 ) final: fState[Steps] fState: wolf: goat: cabbage: cabbageSide: Or( cabbage[i] == 0 , cabbage[i] == 1 ) goatSide: Or( goat[i] == 0 , goat[i] == 1 ) humanSide: Or( human[i] == 0 , human[i] == 1 ) t7: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) t3: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] + 1 ) t6: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] - 1 ) t2: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] + 1 ) , cabbage == cabbage[i] ) t5: And( And( And( humanTravel[i] , wolf == wolf[i] ) , goat[i+1] == goat[i] - 1 ) , cabbage == cabbage[i] ) t1: And( And( And( humanTravel[i] , wolf == wolf[i] + 1 ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) t4: And( And( And( humanTravel[i] , wolf == wolf[i] - 1 ) , goat[i+1] == goat[i] ) , cabbage == cabbage[i] ) safeAlone: And( goat[i+1] != wolf , goat[i+1] != cabbage ) wolfSide: Or( wolf[i] == 0 , wolf[i] == 1 ) humanTravel: human[i] != human[i+1] side: And( And( And( humanSide[i] , wolfSide[i] ) , goatSide[i] ) , cabbageSide[i] ) safe: Or( safeAlone[i] , goat[i+1] == human[i+1] ) objectTravel: Or( Or( Or( Or( Or( Or( t1[i] , t2[i] ) , t3[i] ) , t4[i] ) , t5[i] ) , t6[i] ) , t7[i] ) data: And( And( And( side[i] , safe[i] ) , humanTravel[i] ) , objectTravel[i] )
Les conditions sont triées et insérées dans un modèle de script conçu pour décrire le système SMT en python.
Modèle vierge import json from z3 import * s = Solver() Steps=7 Num= Steps+1 $code$
Pour le dernier état de la chaîne entière, les règles spécifiées dans la section des transactions de transfert s'appliquent.
Ainsi, Z3Prover recherchera exactement un tel ensemble de conditions qui vous permettront éventuellement de retirer des fonds du contrat.
En conséquence, nous obtenons automatiquement un modèle SMT pleinement fonctionnel de notre contrat.
Vous pouvez voir qu'il est très similaire au modèle de mon article précédent, que j'ai écrit manuellement.
Modèle complété import json from z3 import * s = Solver() Steps=7 Num= Steps+1 human = [ Int('human_%i' % (i + 1)) for i in range(Num) ] wolf = [ Int('wolf_%i' % (i + 1)) for i in range(Num) ] goat = [ Int('goat_%i' % (i + 1)) for i in range(Num) ] cabbage = [ Int('cabbage_%i' % (i + 1)) for i in range(Num) ] nothing= [ And( human[i] == human[i+1], wolf[i] == wolf[i+1], goat[i] == goat[i+1], cabbage[i] == cabbage[i+1] ) for i in range(Num-1) ] start= [ human[0] == 1, wolf[0] == 0, goat[0] == 1, cabbage[0] == 0 ] safeAlone= [ And( goat[i+1] != wolf[i+1] , goat[i+1] != cabbage[i+1] ) for i in range(Num-1) ] safe= [ Or( safeAlone[i] , goat[i+1] == human[i+1] ) for i in range(Num-1) ] humanTravel= [ human[i] != human[i+1] for i in range(Num-1) ] cabbageSide= [ Or( cabbage[i] == 0 , cabbage[i] == 1 ) for i in range(Num-1) ] goatSide= [ Or( goat[i] == 0 , goat[i] == 1 ) for i in range(Num-1) ] humanSide= [ Or( human[i] == 0 , human[i] == 1 ) for i in range(Num-1) ] t7= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t3= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] + 1 ) for i in range(Num-1) ] t6= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] - 1 ) for i in range(Num-1) ] t2= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] + 1 ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t5= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] ) , goat[i+1] == goat[i] - 1 ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t1= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] + 1 ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] t4= [ And( And( And( humanTravel[i] , wolf[i+1] == wolf[i] - 1 ) , goat[i+1] == goat[i] ) , cabbage[i+1] == cabbage[i] ) for i in range(Num-1) ] wolfSide= [ Or( wolf[i] == 0 , wolf[i] == 1 ) for i in range(Num-1) ] side= [ And( And( And( humanSide[i] , wolfSide[i] ) , goatSide[i] ) , cabbageSide[i] ) for i in range(Num-1) ] objectTravel= [ Or( Or( Or( Or( Or( Or( t1[i] , t2[i] ) , t3[i] ) , t4[i] ) , t5[i] ) , t6[i] ) , t7[i] ) for i in range(Num-1) ] data= [ Or( And( And( And( side[i] , safe[i] ) , humanTravel[i] ) , objectTravel[i] ) , nothing[i]) for i in range(Num-1) ] fState= And( And( And( human[Steps] == 1 , wolf[Steps] == 1 ) , goat[Steps] == 1 ) , cabbage[Steps] == 1 ) final= fState
Après le lancement, Z3Prover résout un contrat intelligent et nous affiche une chaîne de transactions, ce qui nous permettra de retirer des fonds:
Winning transaction chain found: Data transaction: human= 0, wolf= 0, goat= 1, cabbage= 0 Data transaction: human= 1, wolf= 0, goat= 1, cabbage= 1 Data transaction: human= 0, wolf= 0, goat= 0, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 0, cabbage= 1 Data transaction: human= 0, wolf= 1, goat= 0, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 1, cabbage= 1 Data transaction: human= 1, wolf= 1, goat= 1, cabbage= 1 Transfer transaction
En plus du contrat de transfert, vous pouvez expérimenter vos propres contrats ou essayer cet exemple simple, qui se résout en 2 transactions.
let contract = tx.sender let a= extract(getInteger(contract,"a")) let b= extract(getInteger(contract,"b")) let c= extract(getInteger(contract,"c")) let d= extract(getInteger(contract,"d")) match tx { case t:DataTransaction => let na= extract(getInteger(t.data,"a")) let nb= extract(getInteger(t.data,"b")) let nc= extract(getInteger(t.data,"c")) let nd= extract(getInteger(t.data,"d")) nd == 0 || a == 100 - 5 case s:TransferTransaction => ( a + b - c ) * d == 12 case _ => true }
Comme il s'agit de la toute première version, la syntaxe est très limitée et des bugs peuvent survenir.
Dans les articles suivants, je prévois de mettre en évidence le développement ultérieur de la VM et de montrer comment il est possible de créer des contrats intelligents formellement vérifiés avec son aide, et pas seulement de les résoudre.
Une machine virtuelle symbolique est disponible sur
http://2.59.42.98/hyperbox/Les sources sont disponibles sur github:
http://github.com/scp1001/hyperboxToute la logique VM est contenue dans 2 fichiers, hyperbox.php et hyperbox2.php