Un duo de maths a cartographié un territoire sans fin de surfaces minimales

Un couple de mathématiciens sur la base d'une théorie mathématique peu connue d'il y a 30 ans a démontré que des surfaces minimales ressemblant à un film de savon apparaissent en grand nombre sur un large éventail de figures

Fin 2011, Brian White entendait occasionnellement frapper à la porte de son bureau de Stanford. À l'extérieur, à ces moments, deux jeunes mathématiciens l'attendaient, Fernando Coda Marquez et Andre Nevis , qui avaient toujours la même question: est-ce que White aurait quelques minutes pour les aider à comprendre l'une des parties obscures d'une dissertation peu connue de plusieurs centaines pages écrites il y a trente ans?

La dissertation, écrite par John Pitts , a présenté un mécanisme puissant pour construire des surfaces minimales - des structures similaires au film de savon et aux bulles - dans un large éventail de formes. Lorsqu'une surface minimale peut être construite sur une figure, celle-ci permet d'étudier la géométrie de l'espace qui l'entoure. De telles surfaces apparaissent dans divers problèmes scientifiques, de l'étude des trous noirs au développement de biomolécules.

Et pourtant, toutes ces années, la thèse de Pitts est tombée en dehors du domaine de l'attention des savants - peut-être parce qu'elle était incroyablement difficile à lire. Marquez et Nevis étaient convaincus qu'il y avait un grand potentiel en elle. "Il était évident pour nous que cette théorie était complètement sous-estimée et passée inaperçue", a déclaré Nevis, qui est maintenant professeur à l'Université de Chicago.

Bien que White n'ait jamais demandé au couple pourquoi ils étaient intéressés par le travail de Pitts, ils ont chaque fois déclaré que leur intérêt était «purement académique», a déclaré Nevis. Cependant, ils avaient un objectif précis - prouver l'hypothèse de Wilmore il y a 50 ans, qui aborde la question de trouver la meilleure forme de beignet possible (détails plus loin). Après trois mois de lutte avec les idées de la thèse de Pitts, Marquez et Nevis ont atteint leur objectif , remportant de nombreux prix et critiques positives.

Mais ces dernières années, ils ont pu pousser les idées de Pitts bien plus loin. Pitts, avec son conservateur, Frederick Almgren, a trouvé un moyen de s'assurer que chaque figure dans un petit nombre de dimensions a au moins une surface minimale. Maintenant, Marquez et Nevis, en utilisant la cohorte de jeunes mathématiciens réunis autour d'eux, sur la base des idées d'Almgren et Pitts, ont montré que dans le cas général, ces formes devraient contenir de nombreuses surfaces minimales - infiniment de surfaces encombrées et encombrées dans tous les coins des figures. «C'est une énorme percée», nous a écrit la célèbre géomètre Karen Uhlenbeck de l'Université du Texas dans un e-mail.

«Il faut beaucoup d'efforts pour créer une seule surface minimale», a déclaré Richard Shoin de l'Université de Californie à Irvine, qui a conseillé Nevis il y a environ 15 ans. "Le fait qu'il y en ait tellement est incroyable."

Cette renaissance de la théorie d'Almgren et de Pitts a conduit à une explosion d'activité au cours des deux dernières années. "Les résultats sont si rapides et en si grand nombre qu'il est difficile de les suivre", a déclaré White. "Cela me semble très intéressant et merveilleux."

Marquer la chaîne de montagnes

Trempez le fil incurvé dans une solution savonneuse ou soufflez une bulle de savon et le liquide formera rapidement la surface de la plus petite zone possible. La géométrie de ces surfaces minimales occupe les mathématiciens depuis des centaines d'années. Ils apparaissent dans divers domaines, de l'architecture, où la surface minimale inspire la conception des toits et autres structures, à la création de microparticules pour l'administration de médicaments. Il y a cinq ans, lorsqu'une équipe de scientifiques a créé des molécules poreuses capables de transporter des médicaments ou des hormones en elles, elles ont découvert que certaines molécules prenaient la forme d'une gyroïde , une surface à répétition sans fin, dont certaines parties ressemblent à un film de savon.

Techniquement, les mathématiciens considèrent uniquement les films de savon sur un fil comme des surfaces avec une surface minimale, mais pas des bulles de savon, car dans un espace abstrait où il n'y a pas de molécules d'air, la bulle se détacherait en un point. Cependant, le film sur le fil ne satisfait pas pleinement les mathématiciens. Sa partie intérieure est une surface lisse, mais son fil se rompt fortement. Il est logique de penser s'il est possible d'étendre cette surface au-delà des limites des limites des fils de sorte qu'elle continue à ressembler à un film de savon dans chaque zone individuelle. Parfois, cela est possible et la surface s'étend à l'infini. Parfois, la surface revient et se croise maladroitement avec elle-même, ou rencontre d'autres difficultés.


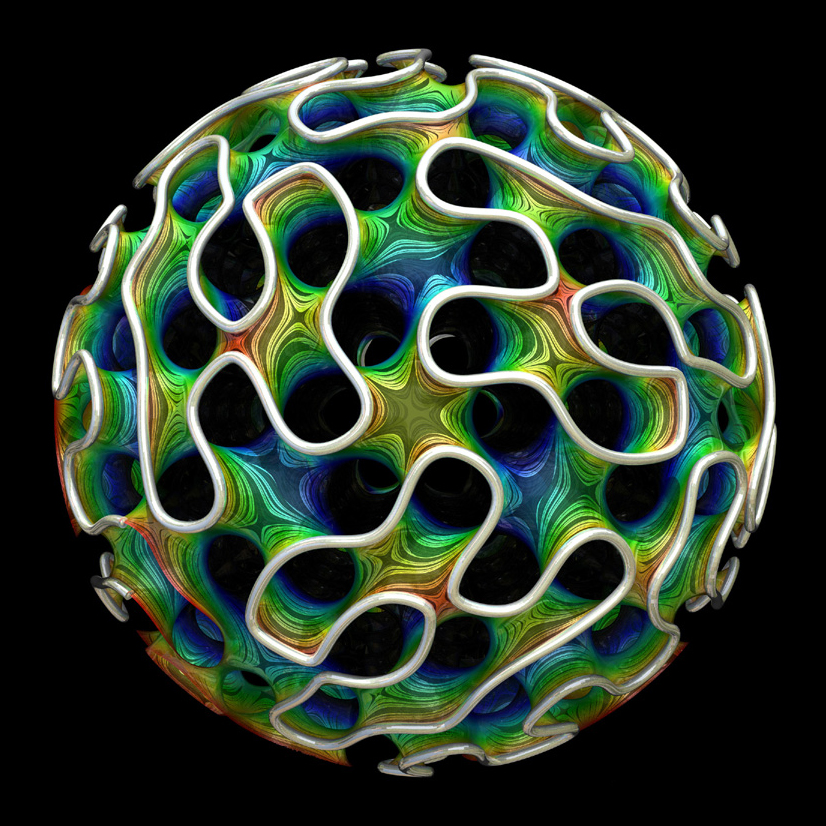Gyroïde - un type de surface minimale qui s'est produite lors de la conception de microparticules pour l'administration de médicaments

Dans l'espace ordinaire, cela épuise toutes les possibilités. Mais les mathématiciens et autres scientifiques considèrent souvent d'autres mondes qui sont différents de l'espace tridimensionnel infini auquel nous sommes habitués - incurvé ou fini, comme les analogies tridimensionnelles d'une sphère ou de la surface d'un tore. De telles figures ont de nouvelles possibilités intéressantes: des surfaces minimales qui se plient sur elles-mêmes et se verrouillent dans une figure finale fermée qui ne nécessite pas de support de fil.

Dans la théorie de la relativité, ces surfaces minimales finies jouent le rôle d'horizon des événements des trous noirs. Et s'ils peuvent être trouvés sur n'importe quelle figure, cela aide les mathématiciens à considérer leur géométrie de différents côtés: ils donnent un modèle pour couper la figure (ou le collecteur ) en morceaux potentiellement plus simples, ils indiquent des zones de courbure positive dans le collecteur - en sections, courbant vers l'intérieur, comme une sphère ou un trou noir, par opposition à courbant vers l'extérieur.

"Nous savons peu de choses sur les variétés à courbure positive", a déclaré Shoin.

Cependant, il est souvent difficile de prouver l'existence d'une surface minimale au sein d'une figure. Pour comprendre pourquoi, envisagez une version bidimensionnelle de ce problème. La question de trouver la surface minimale a un sens dans n'importe quelle dimension: les mathématiciens considèrent simplement la surface comme une forme dont la dimension est inférieure de un à l'espace dans lequel elle vit. Ainsi, dans un monde à deux dimensions, les courbes «géodésiques» constituées des chemins les plus courts reliant les points voisins seront la surface minimale.

Pour certaines figures en deux dimensions, trouvez facilement des courbes géodésiques fermées dans une boucle finie. Prenez la surface d'un tore - même pas nécessairement uniforme et symétrique; laissez-le présenter des irrégularités et des renflements. Si nous enveloppons un tel beignet avec une bande élastique passant par son centre, nous pouvons imaginer comment nous le resserrons et le déplaçons dans diverses positions possibles. L'un d'eux sera le plus court - ce sera par définition une courbe géodésique.



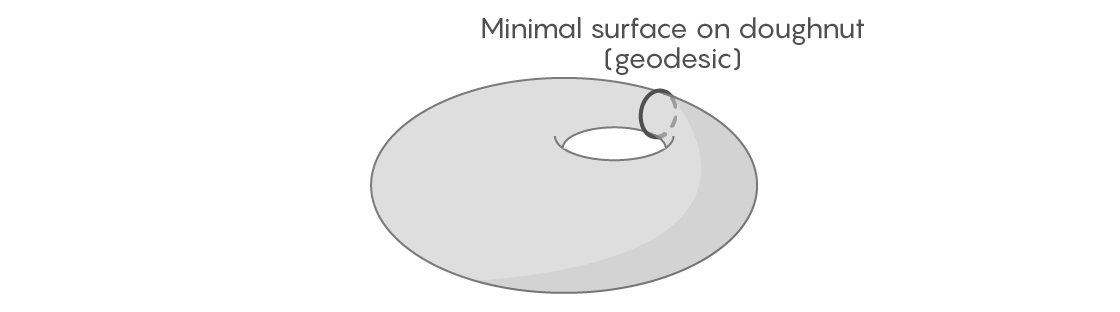
Mais si la sphère est notre figure, cette approche ne fonctionnera plus. Sur une sphère parfaitement plane, il est facile de trouver une courbe géodésique - ce sera l'équateur et d'autres cercles pleins. Mais sur une sphère inégale, par exemple, à la surface de la Terre, il n'est pas clair où vont les courbes géodésiques et si certaines d'entre elles sont fermées en boucle. Vous pouvez imaginer comment nous enveloppons la terre avec une bande élastique, comme dans le cas d'un beignet. Mais si vous commencez à le déplacer, en essayant de le raccourcir, il rétrécira à un point, car contrairement à un beignet, la sphère n'a pas de trou pour que l'élastique s'y accroche.

Cependant, ce fiasco avec une bande élastique est semé d'embûches de succès. Si l'équateur d'une sphère ronde est intercepté par une bande élastique, la seule façon de le déplacer - d'y ajouter des vagues - le rendra plus long. Si vous le déplacez différemment, vers le haut ou vers le bas à une nouvelle latitude, il deviendra plus court. Par conséquent, l'équateur sera la courbe la plus courte d'un point de vue et la plus longue de l'autre.

Cela rend l'équateur lié à la selle du col de montagne, le point le plus élevé d'un côté (du chemin à travers les montagnes) et le plus bas de l'autre (du chemin vers les sommets voisins). Et ce n'est pas seulement une faible analogie: en règle générale, les surfaces minimales s'avèrent être de telles selles, mais leurs chaînes de montagnes vivent dans un monde beaucoup plus difficile à visualiser.



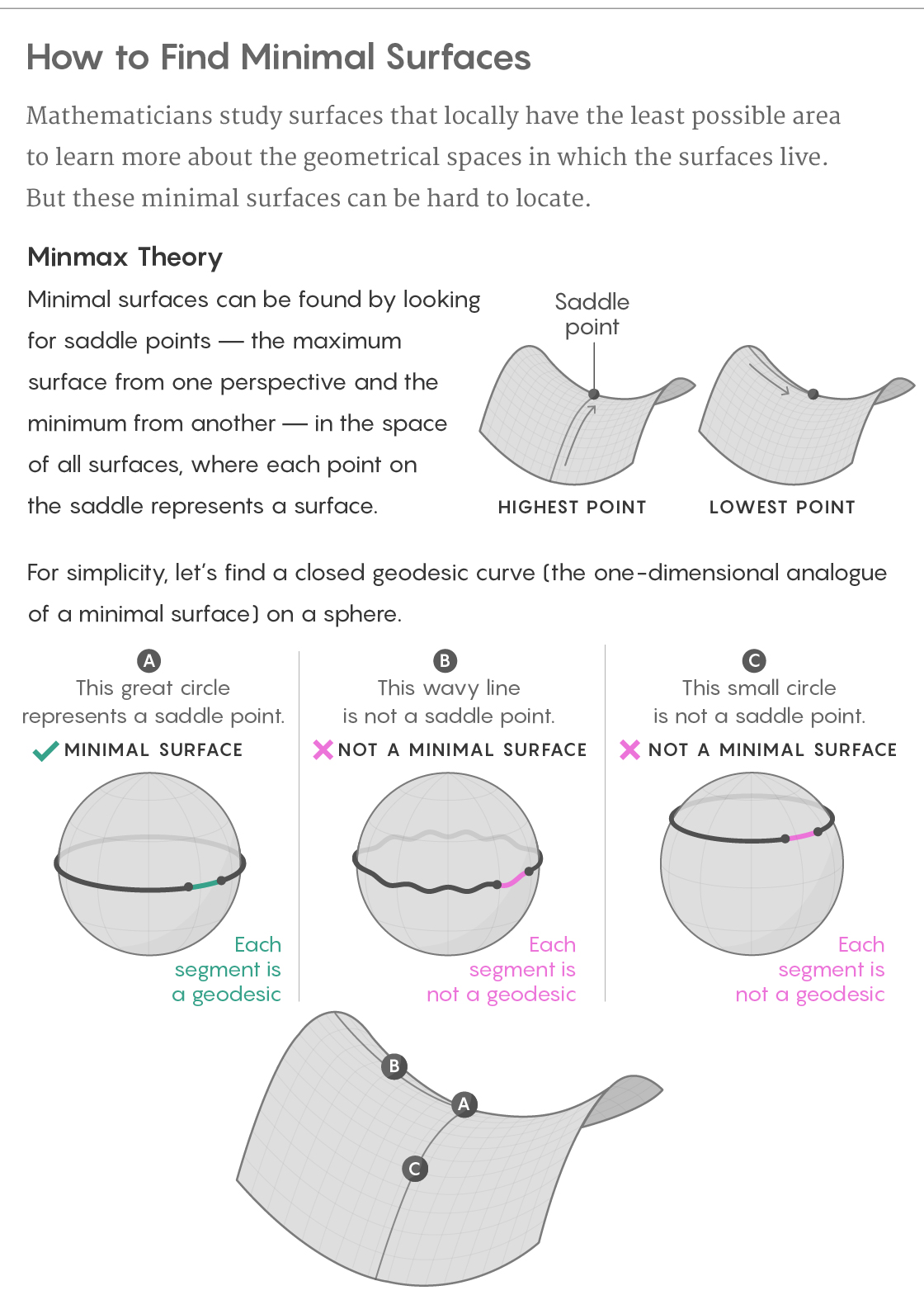
En déterminant la surface minimale d'une figure, nous pouvons considérer un nouveau monde composé de toutes les surfaces finies possibles existant au sein de cette figure - nous l'appellerons la «surface des surfaces». Chaque point de l'espace de surface correspond à la surface entière entièrement sur la figure d'origine. Ensuite, nous pouvons considérer l'aire de chaque surface comme la hauteur du point correspondant dans l'espace des surfaces, à la suite de quoi notre monde aura une topographie naturelle. La recherche de surfaces minimales sur la figure originale devient la recherche de selles dans l'espace de surface.

En 1917, George David Birkhoff a utilisé cette approche pour montrer que toute sphère, vallonnée ou lisse, aura nécessairement une courbe géodésique fermée. Environ six décennies plus tard, Almgren et Pitts ont magistralement étendu les idées de Birkhoff en marquant la topographie de surface des surfaces sur toutes les figures finies en dimensions de trois à sept, puis ont utilisé cette topographie pour prouver que ces figures ont toujours au moins une surface minimale fermée. La thèse de Pitts de 1981 sur cette théorie Minmax - ainsi nommée parce que la selle est à la fois un minimum et un maximum - était "absolument incroyable", a déclaré Nevis.

Cependant, c'était extrêmement complexe. Peu de gens ont compris les nuances de la théorie et certains mathématiciens qui l'ont étudiée ont affirmé qu'elle n'était pas entièrement confirmée, a déclaré Shoin. "Je ne pense pas qu'il y ait eu le moindre doute que c'était extrêmement intéressant et important", a-t-il déclaré. "Mais il n'était pas clair à quel point il était plein."

Les travaux sur la théorie de Minmax ont peu à peu échoué. "Le travail de Pitts a été oublié par la communauté mathématique depuis environ 30 ans", a déclaré Nevis. Elle n'a pas été ressuscitée jusqu'à ce que Nevis et Marquez se rencontrent en 2006 dans l'ascenseur du bâtiment mathématique de l'Université de Princeton.

Au-dessus du col de montagne

À ce moment, Marquez est arrivé à Princeton pour donner une conférence; Nevis y a trouvé un emploi peu de temps après avoir soutenu un doctorat. Les deux avaient le portugais comme langue maternelle (Marquez était du Brésil et Nevis du Portugal), et ils ont facilement trouvé une langue commune. "Ensuite, je lui ai parlé pour la première fois, mais il m'a parlé comme si nous étions amis depuis 10 ans", se souvient Marquez, désormais professeur à Princeton.

Ils ont ensuite découvert que discuter d'idées mathématiques était tout aussi naturel pour eux. Ils ont des styles différents: Marquez est plus calme et Nevis est plus intense. Mais cela a été un plus pour eux. "Il est très rare de trouver quelqu'un qui vous complète si bien", a déclaré Marquez.

Les deux étaient impatients de trouver un problème mathématique complexe qui pourrait être immergé. Pendant plusieurs années, le couple a jeté des idées chaque fois que leurs chemins se croisaient pour "voir ce qui était retardé", a déclaré Nevis. «Nous avions un million d'idées, et en conséquence, l'une d'elles a été filtrée et transformée en quelque chose de formé.»

Le problème filtré s'est avéré être le fameux problème de «l'hypothèse de Wilmore». Elle suggère de trouver une forme de tore qui minimise la magnitude connue sous le nom d'énergie de Willmore, qui, grosso modo, mesure la différence entre une forme donnée et une sphère circulaire. En 1965, Wilmore a suggéré que ce serait le beignet le plus rond d'une forme particulièrement symétrique, connu sous le nom de tore de Clifford , cependant, malgré de nombreuses tentatives, l'hypothèse n'a pu être prouvée à personne.


Marquez (à gauche) et Nevis

Marquez et Nevis ont développé une approche prometteuse, mais pour que cela fonctionne, ils avaient besoin du dernier ingrédient: la théorie minimax. Ils pensaient que la maîtrise de cette théorie et la rédaction du travail final prendraient deux à trois semaines - jusqu'à ce qu'ils ouvrent le livre de Pitts. «Nous avons été choqués - de quoi s'agit-il? - dit Nevis. "Le livre était incroyablement sec."

Les théorèmes séparés se sont développés en plusieurs pages - et ce n'était qu'une description des théorèmes, pas leur preuve. Le théorème principal était simplement difficile à trouver. "Je me souviens comment Fernando est venu dans mon bureau et a dit: j'ai trouvé l'énoncé du théorème!" - dit Nevis.


Thor Clifford

Quand ils se sont retrouvés coincés, ils ont fait du poker et ont demandé de l'aide à White, l'une des rares personnes qui comprenait la plupart du travail de Pitts (bien que White lui-même ait décrit ces conversations comme «aveugles, aveugles de premier plan»; Pitts lui-même, professeur à l'Université A&M du Texas, est diplômé écrire des travaux sur la théorie du minmax il y a quelques décennies). «Nous étions incroyablement motivés et nous avons donc pu percer», se souvient Nevis. "Mais ce n'était pas une tâche pour les faibles de cœur."

Au moment où Marquez et Nevis ont terminé leur preuve de l'hypothèse de Wilmore, ils avaient mieux compris la théorie de Minmax que tout autre mathématicien. Ils étaient convaincus que son potentiel allait bien au-delà de l'énoncé même de l'hypothèse. "Nous savions que nous avions une théorie très puissante", a déclaré Nevis. - Chaque fois, en utilisant la méthode pour prouver un certain résultat qui est resté ouvert depuis longtemps, vous comprenez qu'il y a quelque chose en lui. Cela suggère qu'il vaut la peine de continuer à creuser. "

Le diagramme minmax d'Almgren et Pitts produit non seulement une selle, mais un nombre infini d'entre eux. En théorie, cela devrait correspondre à un nombre infini de surfaces minimales de la forme d'origine. Mais Almgren et Pitts n'ont pas pu montrer que les surfaces minimales ainsi obtenues étaient différentes. Par conséquent, la seule chose que l'on pouvait certainement dire était que chaque figurine avait au moins une surface minimale.

Après cela, "le développement du sujet s'est pratiquement arrêté", a déclaré Nevis. «Ce fut le meilleur résultat sur une période de plus de 30 ans.»

Un nouvel ingrédient était nécessaire, et Marquez et Nevis l'ont trouvé. La liste interminable de surfaces minmax, comme ils l'ont montré en 2016, se comporte de la même manière que les fréquences du tambour.

Le mathématicien allemand Weil en 1911 a montré que les fréquences fondamentales du tambour ont une propriété inattendue: grosso modo, les hautes fréquences ne dépendent que du volume du tambour, et non de sa forme. Marquez et Nevis, avec Eugene Lekumovich du Massachusetts Institute of Technology, ont montré que les surfaces Minmax satisfont à une loi mathématique similaire à la loi des fréquences de tambour. En particulier, les surfaces sont grossièrement déterminées par la quantité d'espace dans lequel elles vivent, et non par sa forme.

Ce résultat, qui a mis fin à l'hypothèse avancée il y a plusieurs décennies, a permis à Marquez et Nevis de montrer en 2017 - cette fois avec l'aide de Kay Air de l'Université de Tokyo - que pour la plupart des figures la liste de minmax contient un nombre infini de surfaces minimales différentes. De plus, ils ont montré que ces surfaces sont «denses»: elles apparaissent à côté de chaque point de l'espace environnant. L'intuition étayant cette conclusion est que pour que le volume d'espace détermine les zones de l'emplacement de surfaces minimales, ces dernières doivent en quelque sorte «voir» le volume entier. Et cela "dit que ces gars sont dans toute leur diversité", a expliqué Marquez.

Quelques mois plus tard, ce couple, avec Antoine Sun , étudiant diplômé de Marques, a montré que si vous parcourez la liste des surfaces minmax, vous verrez qu'elles remplissent l'espace de manière égale - ce que les mathématiciens appellent "équidistribution" apparaît.

"Quand j'ai entendu qu'ils étaient également distribués, j'ai été étonné", a déclaré White. «Il semblait que les gens n'auraient pas dû être en mesure de prouver un tel résultat au cours de ma vie.»

Au cours des deux dernières années, plusieurs autres mathématiciens se sont joints à la question. Par exemple, en janvier, Xin Zhou de l'Université de Californie à Santa Barbara, sur la base de travaux antérieurs de Marquez et Nevis, a prouvé que pour la plupart des figures, toutes les surfaces minimales de la liste Almgren et Pitts sont différentes les unes des autres, ce qui met un point intéressant sur cette question. "Cela clôt vraiment bien ce sujet, ouvert depuis l'époque d'Almgren et de Pitts dans les années 80", a déclaré White.

Cette famille de résultats prend en compte presque tous les chiffres dans des dimensions allant de trois à sept - à l'exception des formes les plus lisses, aussi contraires à l'intuition. Mais en juin dernier, Sunn a pu prouver que chaque figure dans ces dimensions, y compris les plus arrondies, possède une infinité de surfaces minimales fermées, ce qui confirme une autre hypothèse vieille de plusieurs décennies.

On ne sait toujours pas si la densité et l'équidistribution se comporteront aussi uniformément, ainsi que la façon dont la théorie minmax ne fonctionne pas dans des variétés compactes, ou dans huit dimensions ou plus (cependant, les nouveaux travaux ont également connu un certain succès ici). Les mathématiciens prédisent que nous serons en mesure de répondre à de nombreuses questions plus tôt qu'il n'y paraissait.

"Tout se développe extrêmement rapidement", a déclaré Nevis. «Chaque semaine, je regarde le site avec des prépublications arxiv, et je vois comment quelqu'un a décidé autre chose.»

D'un point de vue, ces œuvres marquent la fin - ou la fin - d'une histoire suspendue dans son état inachevé depuis près de quatre décennies. Mais c'est aussi un nouveau départ: les mathématiciens commencent tout juste à comprendre que ces nouvelles idées concernant les surfaces minimales peuvent nous renseigner sur les espaces dans lesquels ils vivent.

"Je peux très bien supposer que d’autres façons intéressantes d’appliquer ces connaissances apparaîtront bientôt, mais quoi exactement, je ne peux certainement pas le dire", a déclaré Shoin. "Je suis sûr que ce sera l'une des principales directions de la géométrie."