Projet: «Taux de change absolu»
Présentation
À propos du projet
Le projet « Taux de change absolu » est engagé dans l'analyse des taux de change appariés, la répartition des taux de change absolus à partir d'eux et leur analyse.
Dans le cadre du projet, une méthodologie de conversion des taux de paire en taux de change absolus a été obtenue. Pour cela, l'ABS en devise absolue est défini. Toutes les devises disponibles sont exprimées en termes d'ABS.
Le projet explore les propriétés des cours absolus. Diverses applications des taux de change absolus sont étudiées.
Pourquoi est-ce ...?
À ce jour, plusieurs articles ont déjà été publiés sur l'application de la méthode du taux de change absolu. J'apporte les deux derniers.
L'article « Étude de l'interdépendance des monnaies mondiales par la corrélation des taux absolus » décrit l'une des applications de la technologie des taux de change absolus. Une méthode formelle de calcul de la relation entre différentes devises est présentée.
L'article « La méthode du portefeuille de Markowitz appliquée au marché des changes » décrit une technologie jusqu'alors inaccessible pour optimiser le portefeuille de devises.
La recherche ne s'arrête pas sur ces deux applications. D'autres applications technologiques sont en cours de test. Si les lecteurs ont leurs propres visions d'autres utilisations possibles, elles peuvent être écrites dans la discussion de l'article. Des liens vers des sites de discussion sont fournis.
Méthodologie d'obtention de cours absolus
Une description détaillée de la technologie est donnée dans l'article « Des paires de devises aux taux de change absolus ».
La méthode est basée sur l'analyse de la présentation des cours en binôme. Un taux de change paire est le rapport entre la valeur d'une devise et la valeur d'une autre. Et si vous introduisez un ABS universel absolu, la transformation suivante a lieu.
Un taux de change paire est le rapport de deux taux absolus.
Afin d'obtenir des cours absolus, vous devez d'abord prologarithme cette équation.
En conséquence, on peut voir que les logarithmes des taux de paire sont linéairement liés aux logarithmes des taux de change absolus. Et cela signifie que vous pouvez rechercher une simple transformation linéaire entre eux. Les logarithmes des cours absolus peuvent être multipliés par la matrice de conversion directe et obtenir les logarithmes des cours appariés.
Et nous devons nous attendre à ce qu'il y ait une transformation linéaire inverse pour la transition des cours par paires aux cours absolus.
En conséquence, toute la méthodologie pour obtenir des cours absolus est écrite comme suit.
Il vous suffit de consigner les cours jumelés, de les multiplier par la matrice inverse et d'appliquer l'exposant.
À propos du problème
Il a été décrit ci-dessus comment obtenir des cours absolus à partir de doubles. Cela se fait à l'aide d'une transformation linéaire des taux de paires logarithmiques et du retour à travers l'exposant.
La conversion linéaire directe des taux absolus en taux appariés est effectuée à l'aide d'une matrice directe. Pour l'obtenir, c'est très simple. Il se compose de zéros, de uns et de moins («0» signifie aucune relation paire / devise, «+1» signifie la devise dans le numérateur de la paire, «-1» signifie la devise dans le dénominateur de la paire). Ci-dessous, vous pouvez le voir.
Le plus gros problème est d'obtenir la matrice inverse (plus précisément, vous devez utiliser la transformation pseudo-inverse ). Avec son aide, vous pouvez passer des cours par paires aux cours absolus. Mais l'obtention de cette matrice n'est pas triviale en raison de la dégénérescence de la matrice de transformation directe.
Dans l'article précédent, une description est donnée d'une méthode pour obtenir une telle matrice. Dans l'article « Détails de la transition des taux de change (relatifs) de paire à absolus. Work on bugs »révèle une méthode pour obtenir des cours absolus. Dans l'expérience, nous avons utilisé la technique de transition vers des composants linéairement indépendants. Ainsi, il a été possible de se débarrasser de la dégénérescence dans la transformation pseudo-inverse.
Méthode de la présente expérience
Dans cet article, une autre méthode pour éviter la dégénérescence dans la matrice de transformation directe est proposée. Actuellement, des cours en binôme sont dispensés par le RBC . Il existe 88 paires de devises à exporter. Pour eux, la matrice de transformation directe suivante existe.
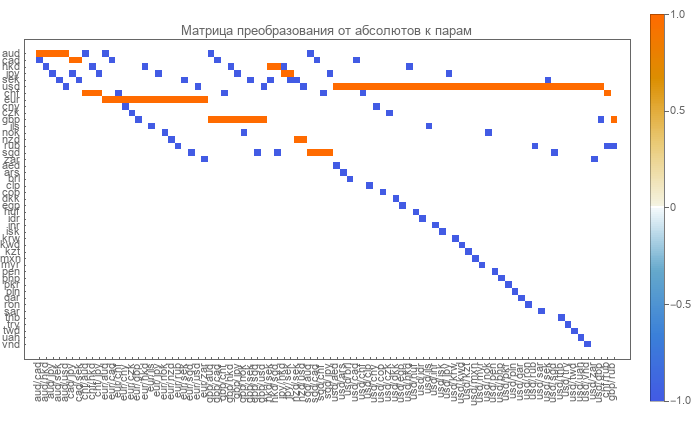
Les zéros blancs, le bleu -1 et le rouge sont des unités. Mais c'est dégénéré. C'est-à-dire il ne produira pas de matrice inverse.
Lors de l'expérience précédente, il a été possible de remarquer qu'une matrice diagonalement similaire a une transformation inverse. En conséquence, il a été proposé de passer aux taux croisés et à une matrice de transformation non dégénérée .
L'ensemble du calcul a été effectué dans le système Wolfram Mathematica . Le système vous permet de recevoir des cours croisés directement à l'intérieur du système .
Détails de l'expérience (petit exemple)
Il y a un total de 45 devises. Pour plus de clarté, nous considérons d'abord le cas avec un petit nombre de devises et de paires de devises. Le calcul est disponible via le lien dans le Wolfram Cloud .
Liste des devises et paires de devises
Les 10 devises suivantes ont été sélectionnées: AUD, CAD, HKD, JPY, SEK, USD, CHF, EUR, CNY, CZK. Parmi celles-ci, 9 paires de devises ont été déterminées: AUD / CAD, CAD / HKD, HKD / JPY, JPY / SEK, SEK / USD, USD / CHF, CHF / EUR, EUR / CNY, CNY / CZK.
Matrice de conversion directe
La matrice de transformation directe a la forme suivante.

La version colorisée ressemble à ceci.

La taille de la matrice est 10x9. Le rang de la matrice est 9. La matrice est non dégénérée. Vous pouvez librement rechercher le contraire.
Matrice de transformation inverse de l'apparié à l'absolu
Grâce à l'application de la méthode de transformation pseudo-inverse, nous obtenons la matrice inverse.

Sous forme colorisée comme ça.

La taille de la matrice inverse est 9x10.
Vérification matricielle inverse
Avant de continuer, vérifiez la matrice résultante. Pour ce faire, nous multiplions la matrice inverse par la droite. Le résultat est le suivant.

Et sous forme colorisée.
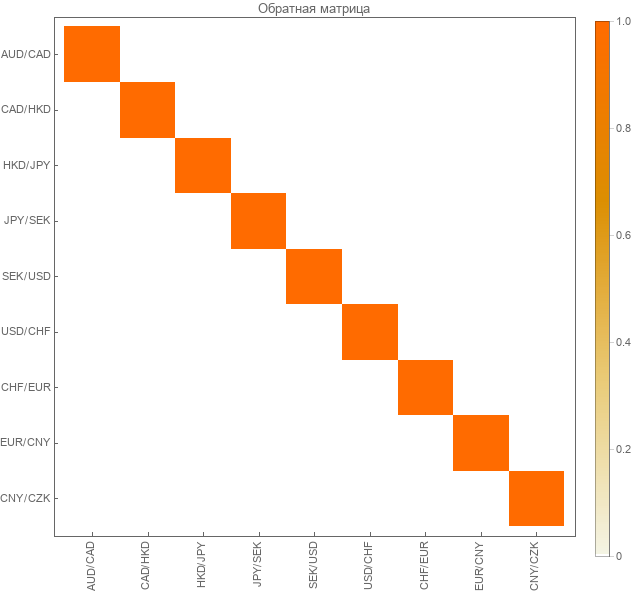
Vraiment obtenu la matrice diagonale unitaire . L'inverse est donc vrai.
Dans une expérience précédente , nous avons testé la méthode d'obtention des taux absolus. Pour cela, à partir des cours absolus obtenus, les cours par paires ont été restaurés via la matrice de conversion directe. Ensuite, nous avons comparé les cours jumelés restaurés avec les cours originaux et examiné l'erreur. Dans notre cas, l'erreur dans un tel contrôle sera dans les limites de la précision de la machine.
Test sur de vrais cours
Voyons maintenant les résultats sur des données réelles. Prenons de vraies citations de taux de change de paire et calculons les taux absolus pour eux.
Nous avons suivi des cours croisés quotidiens pendant 30 jours du 28/03/2019 au 27/04/2019.
Taux de paire de devises
Voici une matrice de taux de change appariés. Ce sont les colonnes des paires de devises pour les paires suivantes AUD / CAD, CAD / HKD, HKD / JPY, JPY / SEK, SEK / USD, USD / CHF, CHF / EUR, EUR / CNY, CNY / CZK.

Voici le graphique de l'une des paires de devises.

Les valeurs moyennes pour les cours en binôme étaient les suivantes.
Essayons maintenant d'évaluer la variabilité des données. Pour ce faire, utilisez l' écart-type . Mais pour la normalisation, nous la divisons par la valeur moyenne. Nous affichons les résultats sur le graphique.
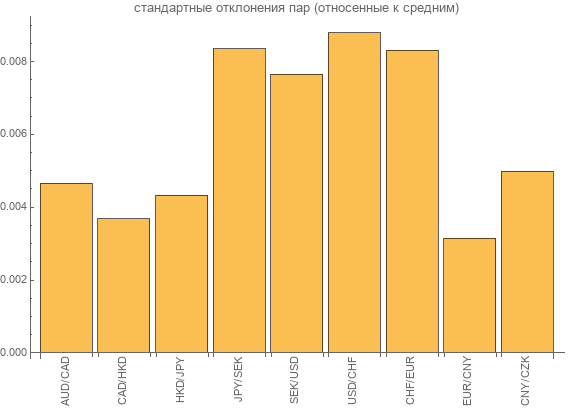
Comme vous pouvez le voir, les écarts-types pour chaque paire de devises sont compris entre 0, 2% - 0, 9% des valeurs moyennes des taux de paire.
Cours absolus
Nous calculons maintenant les cours absolus pour les paires (la méthodologie est décrite dans la section Méthodologie pour obtenir des cours absolus). Après les calculs, nous obtenons la série de données suivante.
Il s'agit de colonnes d'échange absolues pour les devises suivantes AUD, CAD, HKD, JPY, SEK, USD, CHF, EUR, CNY, CZK.

Voici un graphique du taux absolu d'une des devises.
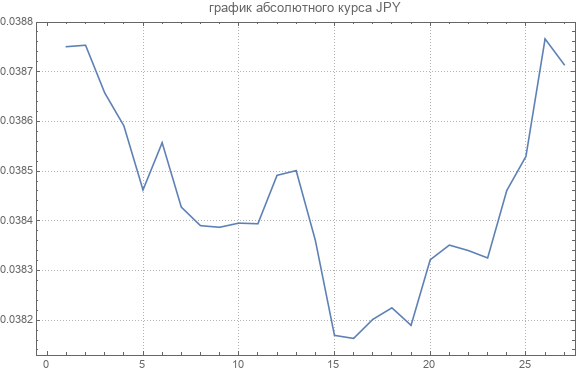
Les valeurs moyennes des cours absolus sont les suivantes.

Nous estimons la variabilité des taux de change absolus.

Les écarts-types pour les taux absolus de chaque devise se situent entre 0, 2% - 0, 7% des valeurs moyennes des taux absolus. Et cela est cohérent avec les données des paires de devises.
Résultats dans toutes les devises
Considérez maintenant les résultats dans toutes les devises disponibles. La source de calcul est disponible ici .
Liste des devises et paires de devises
La liste complète contient les 45 devises suivantes: AUD, CAD, HKD, JPY, SEK, USD, CHF, EUR, CNY, CZK, GBP, ILS, NOK, NZD, RUB, SGD, ZAR, AED, ARS, BRL, CLP, COP , DKK, EGP, HUF, IDR, INR, ISK, KRW, KWD, KZT, MXN, MYR, PEN, PHP, PKR, PLN, QAR, RON, SAR, THB, TRY, TWD, UAH, VND. Les 44 paires de devises suivantes ont été sélectionnées pour elles: AUD / CAD, CAD / HKD, HKD / JPY, JPY / SEK, SEK / USD, USD / CHF, CHF / EUR, EUR / CNY, CNY / CZK, CZK / GBP, GBP / ILS, ILS / NOK, NOK / NZD, NZD / RUB, RUB / SGD, SGD / ZAR, ZAR / AED, AED / ARS, ARS / BRL, BRL / CLP, CLP / COP, COP / DKK, DKK / EGP, EGP / HUF, HUF / IDR, IDR / INR, INR / ISK, ISK / KRW, KRW / KWD, KWD / KZT, KZT / MXN, MXN / MYR, MYR / PEN, PEN / PHP, PHP / PKR, PKR / PLN, PLN / QAR, QAR / RON, RON / SAR, SAR / THB, THB / TRY, TRY / TWD, TWD / UAH, UAH / VND.
Matrice de conversion directe
Nous avons obtenu une matrice de transformation directe de taille 45 par 44. Son rang est 44.
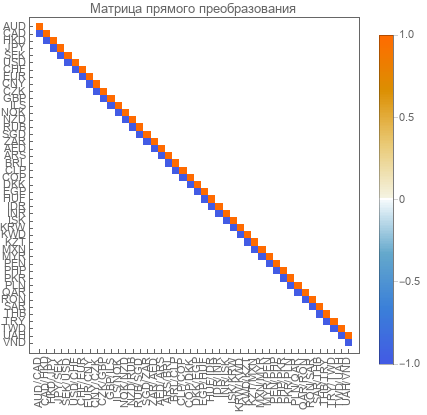
Matrice de transformation inverse
La matrice inverse est le résultat de l'application d'une pseudo-transformation inverse. La taille de la matrice est de 44 par 45.
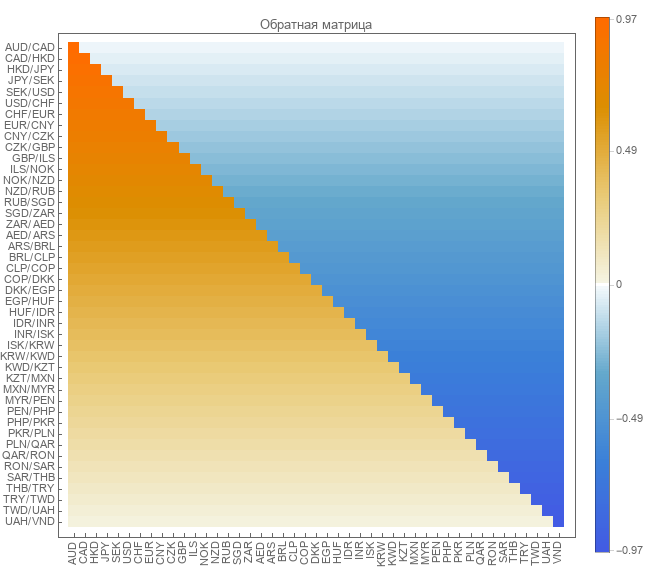
Vérification matricielle inverse
Après avoir multiplié la matrice inverse par la droite, nous avons obtenu la matrice d'identité.
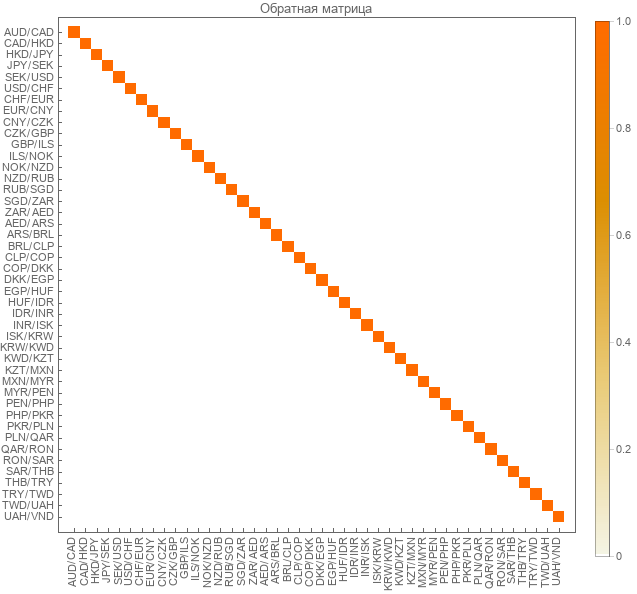
Test sur de vrais cours
A transféré 44 taux de change inter-devises appariés. Un exemple est donné dans le graphique suivant.
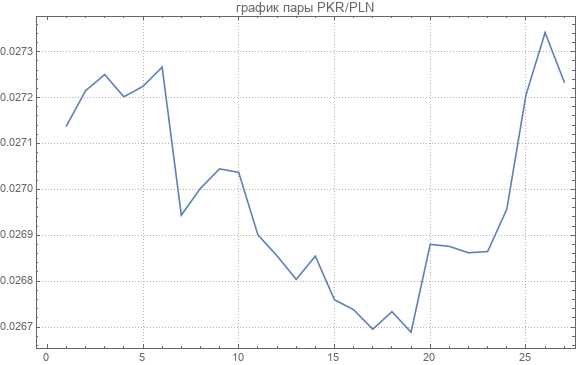
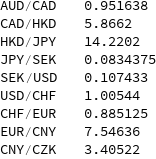
Voici les taux de change moyens pour chaque paire de devises.
AUD / CAD 0.951638
CAD / HKD 5.8662
HKD / JPY 14.2202
JPY / SEK 0,0834375
SEK / USD 0,107433
USD / CHF 1.00544
CHF / EUR 0.885125
EUR / CNY 7,54636
CNY / CZK 3.40522
0,0335481 CZK / GBP
GBP / ILS 4.69022
ILS / NOK 2.38106
NOK / NZD 0.173451
NZD / RUB 43.5338
RUB / SGD 0,0209621
SGD / ZAR 10.4641
ZAR / AED 0,259015
AED / ARS 11.7136
ARS / BRL 0.0907021
BRL / CLP 171.256
CLP / COP 4.72058
COP / DKK 0,00210715
DKK / EGP 2.60095
EGP / HUF 16.5291
HUF / IDR 49.5307
IDR / INR 0,00490364
INR / ISK 1.73912
ISK / KRW 9.44975
KRW / KWD 0.000266945
KWD / KZT 1248.05
KZT / MXN 0,050062
MXN / MYR 0,216251
MYR / PEN 0.803967
PEN / PHP 15.7631
PHP / PKR 2.71475
PKR / PLN 0,0269842
PLN / QAR 0.954411
QAR / RON 1.16298
RON / SAR 0.885697
SAR / THB 8.48908
THB / TRY 0,179564
TRY / TWD 5.39876
TWD / UAH 0,871089
UAH / VND 863.675
Pour chaque paire de devises, nous examinons la variabilité comme dans l'expérience ci-dessus.

L'écart type pour toutes les paires de devises varie de 0,2% à 2,5% de la moyenne.
Après le recomptage, nous obtenons des taux absolus. Voici un graphique du taux absolu d'une des devises.
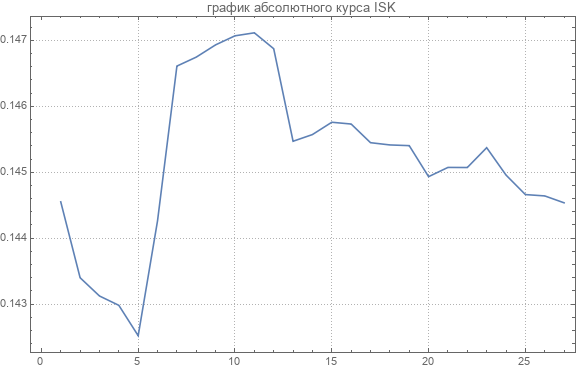
Les valeurs moyennes des taux absolus étaient les suivantes.
AUD 12.4626
13,096 CAD
HKD 2.23247
JPY 0.156996
SEK 1.88165
17,5149 USD
CHF 17.4213
19,6824 EUR
CNY 2.60821
CZK 0,765955
22,832 GBP
ILS 4.86814
NOK 2.04455
NZD 11.7884
RUB 0.270822
SGD 12.9197
ZAR 1.23485
AED 4.76765
ARS 0.407218
BRL 4.49018
CLP 0.0262207
COP 0,0055548
DKK 2.63619
EGP 1.01359
HUF 0,0613224
0,00123809 IDR
0,25249 INR
ISK 0.145194
KRW 0,0153652
KWD 57.5605
KZT 0,0461203
MXN 0.921362
MYR 4.26106
PEN 5.30007
PHP 0,336241
PKR 0.123862
PLN 4.59025
QAR 4.8096
RON 4.1356
SAR 4.66938
THB 0,550046
TRY 3.06473
TWD 0.567676
UAH 0.651731
VND 0.000754602
La variabilité des taux absolus peut être estimée par le diagramme.

L'écart type de tous les taux absolus varie de 0,2% à 2,5% de la moyenne. Ce qui est cohérent avec les données des paires de devises.
Conclusions
L'expérience consistant à obtenir des cours absolus à partir de cours croisés jumelés a été un succès. Une nouvelle méthode de calcul des taux absolus a été obtenue. La méthode fonctionne et est facilement applicable. Pour de plus amples recherches, il est assez facile de recevoir des cours absolus.
L'exactitude de la méthode n'est limitée que par l'exactitude des croisements émis.
Malheureusement, les taux croisés open source sont introuvables sur le réseau. Et en conséquence, cette méthode ne peut pas être appliquée sur le site. Mais dans la comparaison initiale des cours absolus du site et de ceux obtenus dans la présente expérience, les différences n'ont été révélées qu'à la quatrième décimale. Nous effectuerons une comparaison détaillée dans les travaux suivants.
La dernière version de cet article au format PDF peut être téléchargée ici .
Enin A.V.
Orenburg
05/02/2019