Bonjour, Habr!
Cette publication m'a semblé intéressante:
nous obtenons
des taux de change absolus à partir de taux de change croisés et j'ai voulu tester la capacité de trouver ce taux de change absolu par le biais d'une modélisation numérique, en abandonnant généralement l'algèbre linéaire.
Les résultats étaient intéressants.
L'expérience sera petite: 4 devises, 6 paires de devises. Pour chaque paire, une mesure de parcours.
Commençons donc
L'hypothèse est que la valeur de n'importe quelle devise peut être exprimée avec une certaine valeur qui tiendra compte de la valeur des autres devises dans lesquelles elle est cotée, tandis que les autres devises elles-mêmes seront exprimées dans la valeur de toutes les autres devises. Il s'agit d'une tâche récursive intéressante.
Il y a 4 devises:
Pour eux, les paires de devises ont été composées:
- eurusd
- gbpusd
- eurchf
- eurgbp
- gbpchf
- usdchf
Veuillez noter que si le nombre de devises est n = 4, alors le nombre de paires est k = (n ^ 2 - n) / 2 = 6. Cela n'a aucun sens de chercher usdeur si eurusd est cité ...
Au temps t, le taux de change d'un des prestataires a été mesuré:
Des calculs seront effectués pour ces valeurs.
Math
Je résous le problème en prenant analytiquement le gradient de la fonction de perte, qui est essentiellement un système d'équations.
Le code de l'expérience sera en R:
R permet d'utiliser stats :: D pour prendre un dérivé d'une fonction. Par exemple, si nous voulons différencier par la devise USD, nous obtenons l'expression:
2 * (eur / usd ^ 2 * (eurusd - eur / usd)) + 2 * (gbp / usd ^ 2 * (gbpusd -
gbp / usd)) - 2 * (1 / chf * (usdchf - usd / chf))
Pour réduire la valeur de la fonction express, nous allons effectuer une descente de gradient et il est immédiatement clair (nous voyons des différences carrées) que la valeur minimale sera nulle, ce dont nous avons besoin.
-deriv_vals * lr
Le pas de descente de gradient sera régulé par le paramètre lr et tout cela est pris avec un signe négatif.
Autrement dit, nous sélectionnons les taux de 4 devises de sorte que toutes les paires de devises de l'expérience reçoivent des valeurs égales aux valeurs initiales de ces paires. Mmm, résolvons le puzzle - dans le front!
Résultats
Afin de ne pas étirer, je vais immédiatement vous informer de ce qui suit: l'expérience dans son ensemble a réussi, le code a fonctionné, l'erreur s'est rapprochée, proche de zéro. Mais j'ai remarqué que les résultats sont toujours différents.
Une question pour les connaisseurs: il semble que cette tâche ait un nombre illimité de solutions, mais en cela je suis un zéro complet, je pense qu'ils me le diront dans les commentaires.
Pour vérifier la (dé) stabilité de la solution, j'ai simulé 1000 fois sans fixer la graine PRNG pour les valeurs de départ des valeurs monétaires.
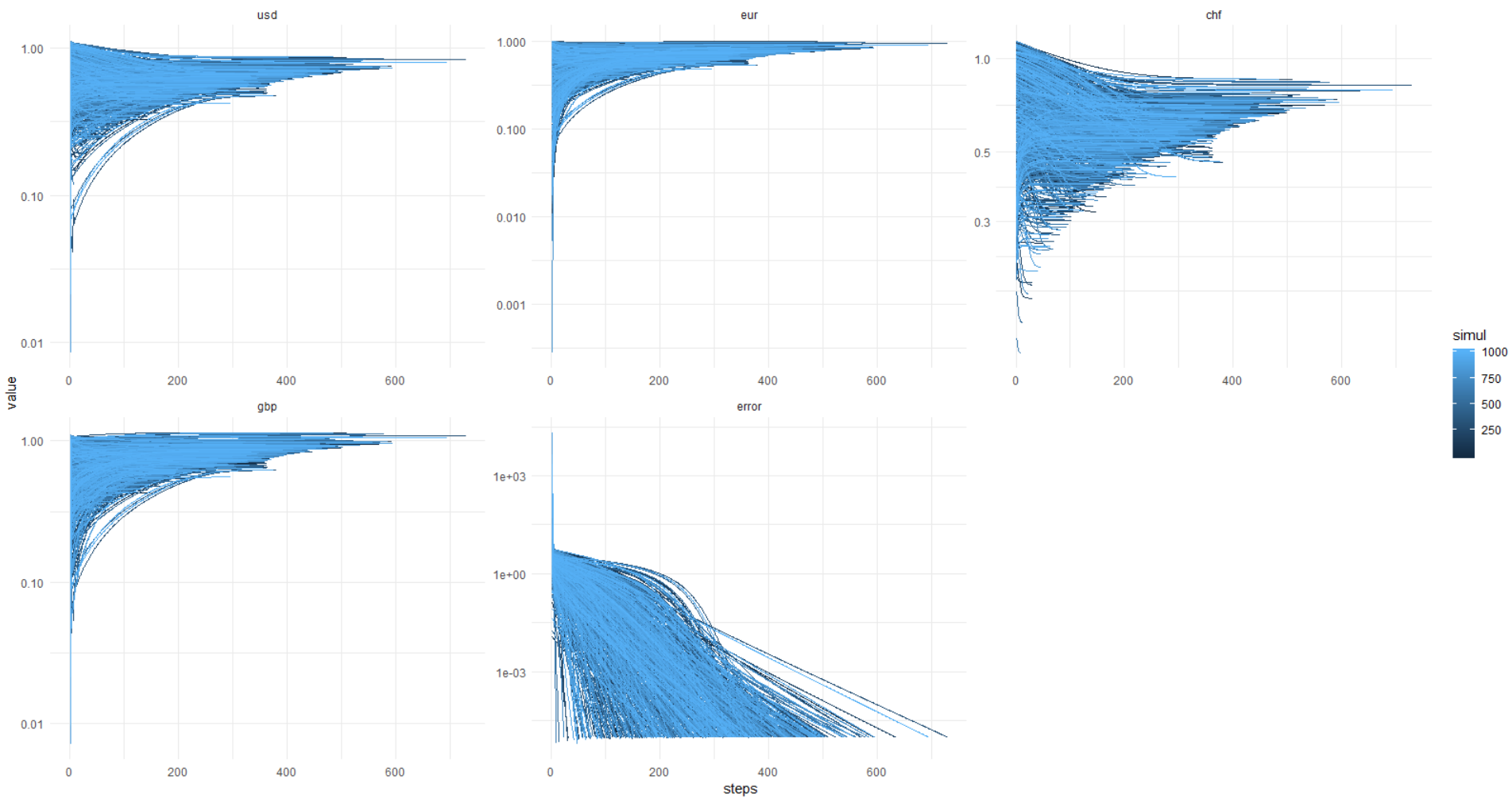
Et voici l'image du kata: l'erreur atteint toujours 0,00001 et moins (l'optimisation est définie de cette façon), tandis que les valeurs des devises flottent de partout. Il s'avère qu'il y a toujours une décision différente, messieurs!
Encore une fois, cette image, l'axe des y dans les unités d'origine (pas log.):
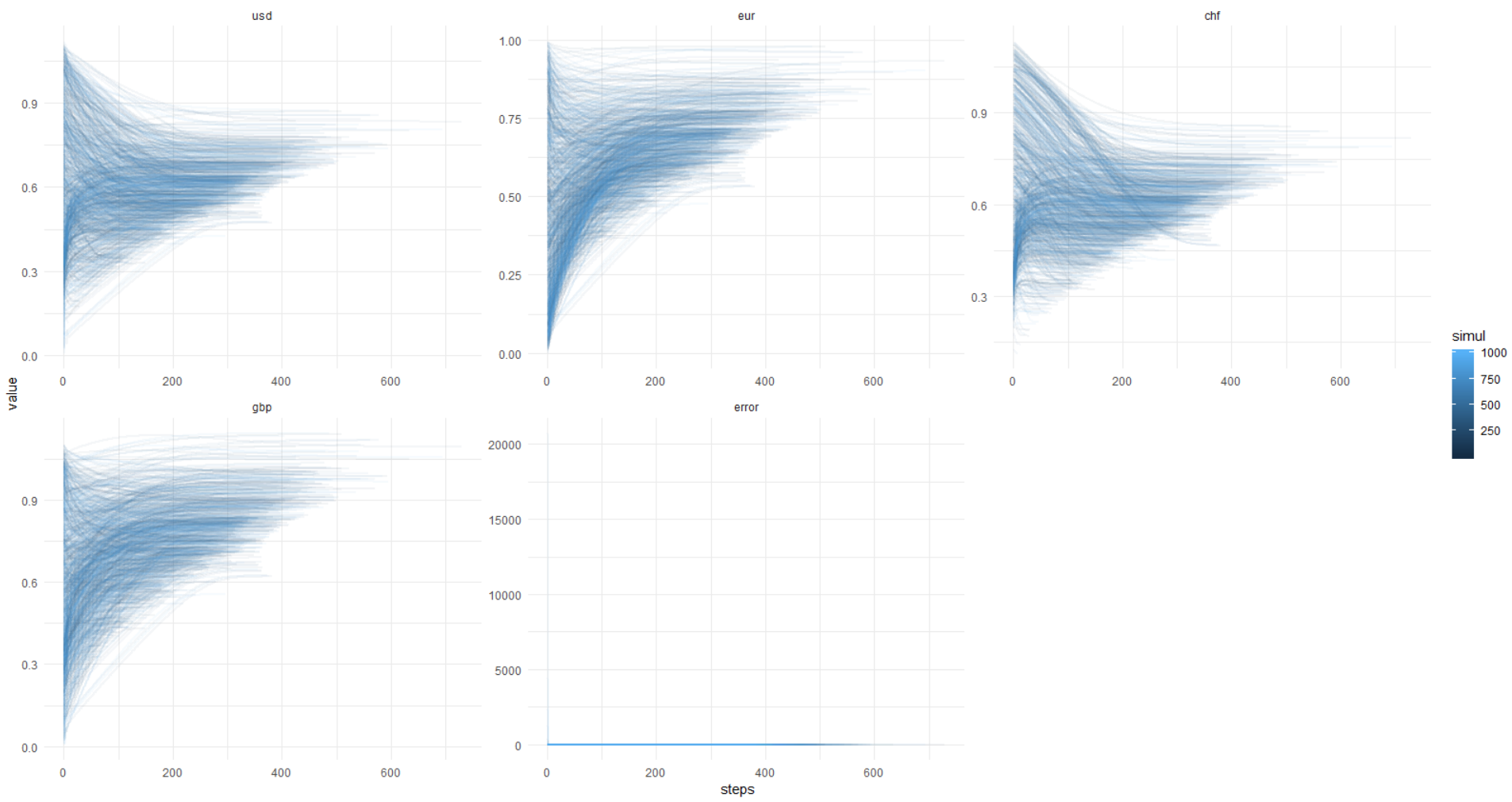
Pour que vous puissiez répéter cela, ci-dessous, je joins le code complet.
Le code pour 1000 simulations fonctionne pendant environ une minute.Conclusion
Voici ce qui ne me paraît pas clair:
- Est-il possible de stabiliser la solution d'une manière mathématique délicate;
- s'il y aura une convergence avec plus de devises et de paires de devises;
- s'il n'y a pas de stabilité, alors pour chaque nouvel instantané de données, nos devises marcheront comme elles le souhaitent, si vous ne corrigez pas la graine PRNG, et c'est un échec.
L'idée globale semble très vague en l'absence de conditions préalables et de limitations intelligibles. Mais c'était intéressant!
Eh bien, je voulais aussi dire que l'on peut se passer d'OLS lorsque les données sont délicates, les matrices sont singulières, enfin, ou lorsque la théorie est mal connue (ehh ...).
Merci
eavprog pour le message initial.
Salut!