Préface

En plus de mon récent article, je voudrais également parler du sujet MU ( M ulti U ser) MIMO. J'ai déjà mentionné le très célèbre article du professeur Haardt où, avec ses collègues, il propose un algorithme de séparation des utilisateurs dans une liaison descendante basé sur des méthodes linéaires, à savoir la diagonalisation de bloc d'un canal. L'article contient un nombre impressionnant de citations et constitue également la publication fondamentale pour l'une des tâches d'examen. Par conséquent, pourquoi ne pas découvrir les bases de l'algorithme proposé?

Énoncé du problème

Tout d'abord, décidons dans quel domaine du thème MIMO nous allons travailler maintenant.
Classiquement, toutes les méthodes de transfert dans le cadre de la technologie MIMO peuvent être divisées en deux groupes principaux:

• Diversité spatiale

L'objectif principal est d'augmenter l'immunité au bruit de la transmission. Les canaux spatiaux, s'ils sont simplifiés, se dupliquent, ce qui nous permet d'obtenir la meilleure qualité de transmission.

Exemples:
- Codes de bloc (par exemple, le schéma Alamuti );
- Codes basés sur l'algorithme de Viterbi.

• Multiplexage spatial

L'objectif principal est d'augmenter la vitesse de transmission. Nous avons déjà expliqué dans un article précédent que sous certaines conditions le canal MIMO peut être considéré comme une série de canaux SISO parallèles. En fait, c'est l'idée centrale du multiplexage spatial: obtenir le maximum de flux d'informations indépendants. Le problème principal dans ce cas est la suppression des interférences inter-canaux (inter-canaux) , pour lesquelles il existe plusieurs classes de solutions:

- séparation horizontale des canaux;
- vertical (par exemple, l'algorithme V-BLAST);
- diagonale (par exemple, l'algorithme D-BLAST).

Mais ce n'est bien sûr pas tout.

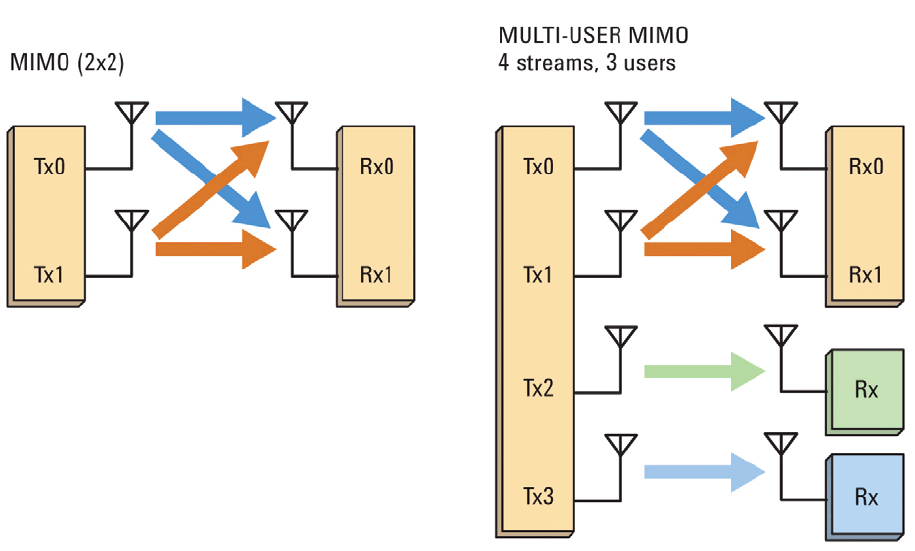
L'idée du multiplexage spatial peut être élargie: diviser non seulement les canaux, mais aussi les utilisateurs (SDMA - Space Division Multiple Access).

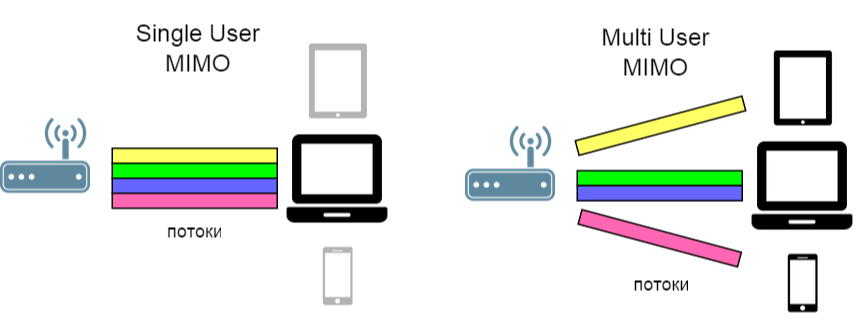
( lien vers la source de l'illustration )

Par conséquent, dans ce cas, il est déjà nécessaire de lutter contre les interférences entre utilisateurs . Pour cela, un algorithme appelé Block diagonalization Zero-Forcing a été proposé , que nous envisageons aujourd'hui.

Description mathématique

Commençons, comme précédemment, par le modèle de signal reçu. Plus précisément, nous montrons sur le diagramme d'où et d'où vient:

La matrice des canaux dans ce cas a la forme:

avec le nombre total d'antennes d'émission et le nombre total d'antennes de réception .

Important :
Cet algorithme ne peut être appliqué que si le nombre d'antennes d'émission est supérieur ou égal au nombre total d'antennes de réception:

Cette condition affecte directement les propriétés de la diagonalisation.

Ainsi, le modèle des symboles (signaux) reçus peut être écrit sous forme vectorielle comme:

Cependant, il est plus intéressant de regarder la formule pour un utilisateur spécifique:

En fait:

• Est un signal utile pour le k-ème utilisateur,

  
  

• - c'est une interférence d'autres utilisateurs,

  
  

• - bruit additif.

Nous arrivons donc à la formulation de la tâche principale:

Vous pouvez trouver de telles matrices de sorte que la partie d'interférence passe à zéro!

Voilà ce que nous allons faire.

Description de l'algorithme

Nous allons effectuer la description avec un exemple, et à titre d'illustration, je donnerai des captures d'écran de première main , en les commentant un peu.

Considérez le premier utilisateur:

Parlons des principales étapes:

• Nous faisons une matrice des matrices de canaux de tous les autres utilisateurs.

• Nous le décomposons en utilisant la méthode SVD .

  
  

• Dans la matrice nous trouvons le sous-espace de bruit (sous-espace nul) - la matrice (c'est-à-dire tout ce qui dépasse le rang de la matrice - le dénoter )

  
  

• Nous composons à partir de cette matrice de bruit et de sa conjugaison hermitienne une matrice de projection .

  
  

Allez-y:

• Maintenant, la partie originale de la matrice des canaux multiplier avec la matrice de projection résultante .

  
  

• Nous décomposons le résultat via SVD.

  
  

• Dans la matrice choisir lignes où - rang .

  
  

• Transposez-les et obtenez la matrice (ou - où comme indiqué).

  
  

Et donc cette procédure sera répétée pour chaque utilisateur. N'est-ce pas la magie des mathématiques: en utilisant les méthodes de l'algèbre linéaire, nous résolvons des problèmes complètement techniques!

Notez qu'en pratique, non seulement les matrices de pré-codage obtenues sont utilisées, mais aussi les matrices de post-traitement et la matrice de valeurs singulières (voir diapositives ). Ce dernier, par exemple, permet d'équilibrer la puissance selon l' algorithme de coulée d'eau déjà connu.

Nous modélisons l'algorithme

Je pense qu'il ne sera pas superflu d'effectuer une petite simulation pour consolider le résultat. Pour ce faire, nous utiliserons Python 3, à savoir:

import numpy as np 

pour les calculs de base, et:

 import pandas as pd 

pour afficher le résultat.

 class ZeroForcingBD: def __init__(self, H, Mrs_arr): Mr, Mt = np.shape(H) self.Mr = Mr self.Mt = Mt self.H = H self.Mrs_arr = Mrs_arr def __routines(self, H, mr, shift): # used in self.process() - See example above for illustration # inputs: # H - the whole channel matrix # mr - number of receive antennas of the i-th user # shift - how much receive antennas were considered before # outputs: # Uidx, Sigmaidx, Vhidx - SVD decomposition of the H_iP_i # d - rank of the hat H_i # Hidx - H_i (channel matrix for the i-th user) # r - rank of the H_i Hidx = H[0+shift:mr+shift,:] # H_i (channel matrix for the i-th user) r = np.linalg.matrix_rank(Hidx) # rank of the H_i del_idx = [i for i in range(0+shift, mr+shift, 1)] # row indeces of H_i in H H_hat_idx = np.delete(H, del_idx, 0) # hat H_i d = np.linalg.matrix_rank(H_hat_idx) # rank of the hat H_i U, Sigma, Vh = np.linalg.svd(H_hat_idx) # SVD Vhn = Vh[d:, :] # null-subspace of V^H Vn = np.matrix(Vhn).H # null-subspace of V Pidx = np.dot(Vn, np.matrix(Vn).H) # projection matrix Uidx, Sigmaidx, Vhidx = np.linalg.svd(np.dot(Hidx, Pidx)) # SVD of H_iP_i return Uidx, Sigmaidx, Vhidx, d, Hidx, r def process(self): # used in self.obtain_matrices() # outputs: # F - whole filtering (pre-coding) matrix (array of arrays) # D - whole demodulator (post-processing) matrix (array of arrays) # H - the whole channel matrix (array of arrays) shift = 0 H = self.H F = [] D = [] Hs = [] for mr in self.Mrs_arr: Uidx, Sigmaidx, Vhidx, d, Hidx, r = self.__routines(H, mr, shift) Vhidx1 = Vhidx[:r,:] # signal subspace Fidx = np.matrix(Vhidx1).H F.append(Fidx) D.append(Uidx) Hs.append(Hidx) shift = shift + mr return F, D, Hs def obtain_matrices(self): # used to obtain pre-coding and post-processing matrices # outputs: # FF - whole filtering (pre-coding) matrix # DD - whole demodulator (post-processing) matrix (array of arrays) F, D, Hs = self.process() FF = np.hstack(F) # Home Task: calculation of the demodulator matrices :) return FF 

Supposons que nous ayons 8 antennes d'émission et 3 utilisateurs qui ont respectivement 3, 2 et 3 antennes de réception:

 Mrs_arr = [3,2,3] # 1st user have 3 receive antennas, 2nd user - 2 receive antennas, 3d user - 3 receive antennas Mr = sum(Mrs_arr) # total number of the receive antennas Mt = 8 # total number of the transmitt antennas H = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2); #Rayleigh flat faded channel matrix (MrxMt) 

Nous initialisons notre classe et appliquons les méthodes appropriées:

 BD = ZeroForcingBD(H, Mrs_arr) F, D, Hs = BD.process() FF = BD.obtain_matrices() 

Nous apportons sous une forme lisible:

 df = pd.DataFrame(np.dot(H, FF)) df[abs(df).lt(1e-14)] = 0 

Et prenons un peu d'ascenseur pour plus de clarté (bien que vous puissiez vous en passer):

 print(pd.DataFrame(np.round(np.real(df),100))) 

Vous devriez obtenir quelque chose comme ceci:

En fait, ici ce sont des blocs, ça y est et la diagonalisation. Et minimiser les interférences.

De telles choses.

Littérature

1. Spencer, Quentin H., A. Lee Swindlehurst et Martin Haardt. "Méthodes de forçage nul pour le multiplexage spatial en liaison descendante dans les canaux MIMO multi-utilisateurs." Transactions IEEE sur le traitement du signal 52.2 (2004): 461-471.
2. Martin Haard " Traitement de transmission robuste pour les systèmes MIMO multi-utilisateurs "

PS

Au corps enseignant et à la fraternité étudiante de ma profession natale, je dis bonjour!