Depuis de nombreuses années, je donne des cours de combinatoire et de graphisme à des étudiants en mathématiques et en informatique (comment est-il en russe, en informatique?), Auparavant à l'Université universitaire et maintenant à
l'Université d'État de Saint-Pétersbourg . Notre programme est conçu de manière à ce que ces sujets soient abordés dans le cadre de «l'informatique théorique» (d'autres sujets y sont les algorithmes, la complexité, les langages et les grammaires). Je ne peux pas dire comment métaphysiquement ou historiquement justifié: néanmoins, les objets combinatoires (graphes, systèmes de décors, permutations, figures quadrillées, etc.) ont commencé à être étudiés bien avant l'avènement des ordinateurs, et maintenant ce dernier, bien qu'important, est loin d'être le seul motif d'intérêt pour lui. Mais regarder les spécialistes de la combinatoire et de l'informatique théorique, c'est étonnamment souvent les mêmes personnes: Lovas, Alon, Semeredi, Razborov et au-delà. Il y a probablement des raisons à cela. Dans mes cours, les champions de la programmation olympique offrent souvent des solutions très simples à des problèmes complexes (je ne les énumérerai pas, à quiconque est curieux de voir les meilleurs codes). En général, je pense que certaines choses de la combinatoire peuvent intéresser la communauté. Parlez si quelque chose est vrai ou non.
Laissez-vous besoin de construire une permutation aléatoire de nombres de 1 à
$ en ligne $ n $ en ligne $ de sorte que toutes les permutations sont également probables. Cela peut être fait de plusieurs manières: par exemple, sélectionnez d'abord au hasard le premier élément, puis à partir du second restant et ainsi de suite. Ou vous pouvez faire autrement: sélectionnez des points au hasard
$ inline $ t_1, t_2, \ ldots, t_n $ inline $ dans le segment
$ inline $ [0,1] $ inline $ et voyez comment ils sont commandés. En remplaçant le plus petit des nombres par 1, le second par 2, etc., nous obtenons une permutation aléatoire. Facile à voir que tout
$ inline $ n! $ inline $ les permutations sont également probables. C'est possible et pas dans le segment
$ en ligne $ 0,1 $ en ligne $ choisir des points et, par exemple, parmi les nombres de 1 à
$ en ligne $ n $ en ligne $ . Ici, les coïncidences sont possibles (pour un segment, elles sont également possibles, mais avec une probabilité nulle, donc elles ne nous dérangent pas) - vous pouvez les traiter de différentes manières, par exemple, en réordonnant en plus les numéros correspondants. Ou prendre
N plus grand pour que la probabilité de coïncidence soit petite (le cas
$ en ligne $ N = 365 $ en ligne $ et
$ en ligne $ n $ en ligne $ il y a le nombre d'élèves dans votre classe, et nous parlons de la coïncidence de deux anniversaires.) Une variation sur cette méthode: notez au hasard
$ en ligne $ n $ en ligne $ points dans un carré d'unité et voir comment leurs ordonnées sont ordonnées par rapport aux abscisses. Autre variation: marque dans le segment
$ en ligne $ n-1 $ en ligne $ pointer et voir comment les longueurs des segments dans lesquels il est divisé sont ordonnées. Le point clé de ces approches est l'indépendance des tests, selon les résultats desquels un réarrangement aléatoire est construit. Andrei Nikolaevich Kolmogorov a déclaré que la théorie des probabilités est une théorie de la mesure plus l'indépendance - et cela sera confirmé par tous ceux qui ont traité la probabilité.
Je vais montrer comment cela aide, en utilisant l'exemple de la
formule des crochets pour les arbres :
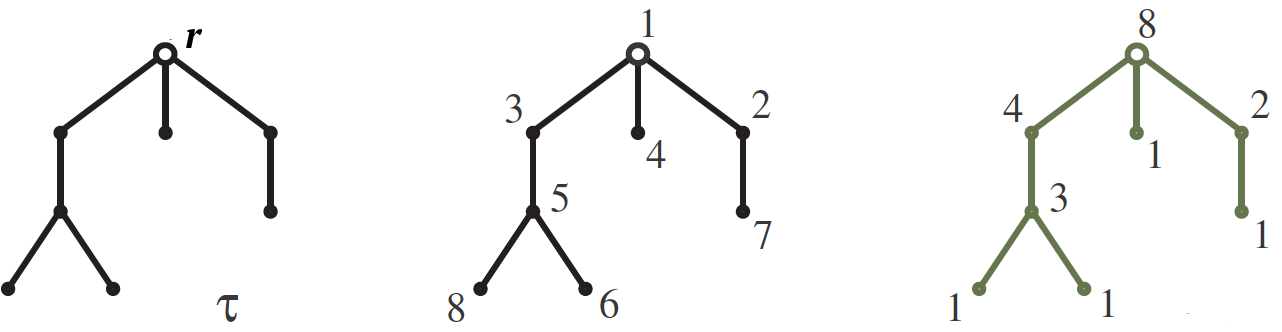
Soit
$ inline $ \ tau $ inline $ - suspendu par la racine
$ en ligne $ r $ en ligne $ arbre avec
$ en ligne $ n $ en ligne $ pics qui poussent comme sur la photo. Notre objectif est de calculer le nombre
$ inline $ S (\ tau) $ inline $
numéroter les sommets des arbres
$ inline $ \ tau $ inline $ nombres de 1 à
$ en ligne $ n $ en ligne $ de telle sorte que pour chaque bord, le nombre en haut est supérieur à celui en bas. L'un de ces chiffres est illustré dans l'image du milieu. La réponse est formulée en utilisant des
tailles de crochets . Crochet
$ en ligne $ H (v) $ en ligne $ pics
$ inline $ v $ inline $ appelons un sous-arbre croissant à partir de ce sommet, et sa taille est simplement le nombre de sommets qu'il contient. Les longueurs de crochet sont écrites dans l'image de droite à côté des sommets correspondants. Ainsi, le nombre de nombres est
$ inline $ n! $ inline $ divisé par le produit des tailles de crochet, donc pour notre exemple
$$ afficher $$ S (\ tau) = \, \ frac {8!} {8 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 \ cdot 1 \ cdot 1 \ cdot 1} = 210. $$ afficher $ $
Nous pouvons prouver cette formule de différentes manières, par exemple par induction sur le nombre de sommets, mais notre vision des permutations aléatoires nous permet d'effectuer la preuve sans aucun calcul. C'est mieux non seulement par l'élégance, mais aussi parce qu'il se généralise bien à des questions plus subtiles sur la numérotation avec les inégalités prescrites, mais pas à ce sujet maintenant. Donc, prenez
n nombres réels différents et placez-les au hasard en haut de l'arbre, chacun avec un numéro, tous
$ inline $ n! $ inline $ les permutations sont également probables. Quelle est la probabilité que pour chaque arête, le nombre au sommet supérieur de l'arête soit supérieur au nombre à son sommet inférieur? La réponse est:
$ inline $ S (\ tau) / n! $ inline $ , et cela ne dépend pas d'un ensemble de nombres. Et si cela ne dépend pas, alors considérons les nombres également choisis au hasard - pour être précis, dans l'intervalle
$ inline $ [0,1] $ inline $ . Au lieu de sélectionner au hasard des nombres dans un premier temps, puis de les disposer de manière aléatoire en haut de l'arbre, nous pouvons simplement sélectionner de manière aléatoire et indépendante un nombre à chaque sommet: leur réarrangement sera aléatoire automatiquement. De cette façon
$ inline $ S (\ tau) / n! $ inline $ c'est la probabilité que pour des nombres indépendants aléatoires
$ en ligne $ \ xi (v) $ en ligne $ sélectionné un pour chaque sommet
$ inline $ v $ inline $ bois
$ inline $ \ tau $ inline $ , toutes les inégalités de la forme
$ inline $ \ xi (v)> \ xi (u) $ inline $ pour tous les bords
$ inline $ v \ à u $ inline $ ,
$ inline $ v $ inline $ Est le sommet supérieur de la côte, et
$ en ligne $ u $ en ligne $ - en bas. Nous formulons ces conditions sous une forme équivalente, mais de manière légèrement différente: pour chaque sommet
$ inline $ v $ inline $ un tel événement devrait se produire - je le désignerai
$ en ligne $ Q (v) $ en ligne $ : nombre
$ en ligne $ \ xi (v) $ en ligne $ - le maximum parmi tous les nombres aux sommets du sous-arbre du crochet
$ en ligne $ H (v) $ en ligne $ .
Notez que
$ inline $ \ frac {1} {| H (v) |} $ inline $ c'est la probabilité d'un événement
$ en ligne $ Q (v) $ en ligne $ . En fait, dans le crochet
$ en ligne $ H (v) $ en ligne $ est disponible
$ en ligne $ | H (v) | $ en ligne $ sommets et le nombre maximal de crochets est mappé à chacun d'eux avec une probabilité égale
$ inline $ \ frac {1} {| H (v) |} $ inline $ . Donc, la formule du crochet
$ inline $ S (\ tau) / n! = \ prod_v \ frac {1} {| H (v) |} $ inline $ peut être formulée comme suit: la probabilité que tous les événements se produisent en même temps
$ en ligne $ Q (v) $ en ligne $ est égal au produit des probabilités de ces événements. Les raisons peuvent être différentes, mais la première qui vient à l'esprit fonctionne ici: ces événements sont indépendants. Pour comprendre cela, regardons, par exemple, un événement
$ en ligne $ Q (r) $ en ligne $ (correspondant à la racine). Il consiste dans le fait que le nombre dans la racine est supérieur à tous les autres nombres dans les sommets, et d'autres événements se rapportent à des comparaisons entre eux de nombres écrits pas dans la racine. C’est
$ en ligne $ Q (r) $ en ligne $ concernant le nombre
$ en ligne $ \ xi (r) $ en ligne $ et des
ensembles de nombres aux autres sommets, et tous les autres événements sont de l'
ordre des nombres aux sommets autres que la racine. Comme nous l'avons déjà évoqué, «ordre» et «multitude» sont indépendants, donc l'événement
$ en ligne $ Q (r) $ en ligne $ indépendant des autres. En descendant dans l'arbre, nous obtenons que tous ces événements sont indépendants, d'où le nécessaire suit.
Habituellement, la formule pour les crochets est la formule pour numéroter non pas les sommets de l'arborescence, mais les cellules
du diagramme Young 
augmentant dans les directions des axes de coordonnées, et les crochets y ressemblent plus à des crochets qu'à des arbres. Mais cette formule se révèle plus compliquée et mérite un poste séparé.
Depuis que je l'avais d'ailleurs, je ne peux m'empêcher de parler du modèle d'un
diagramme de Young aléatoire . Le jeune diagramme est une telle figure de
$ en ligne $ n $ en ligne $ carrés d'unité, la longueur de ses lignes augmente de bas en haut et la longueur des colonnes de gauche à droite. Nombre de graphiques de zone de Young
$ en ligne $ n $ en ligne $ est indiqué
$ en ligne $ p (n) $ en ligne $ , cette
fonction importante se comporte de manière intéressante et inhabituelle: par exemple, elle croît plus vite que n'importe quel polynôme, mais plus lentement que tout exposant. Par conséquent, en particulier, générez un diagramme de Young aléatoire (si nous voulons que tous les diagrammes de surface
$ en ligne $ n $ en ligne $ étaient tout aussi probables
$ en ligne $ 1 / p (n) $ en ligne $ ) n'est pas anodin. Par exemple, si vous ajoutez des cellules une par une, en choisissant un endroit pour ajouter au hasard, différents graphiques auront des probabilités différentes (ainsi, la probabilité d'un graphique à une seule ligne se révèle être égale
$ en ligne $ 1/2 ^ {n-1} $ en ligne $ .) Il s'avère une mesure divertissante sur les diagrammes, mais pas uniforme. L'uniforme peut être obtenu comme suit. Prenez le numéro
$ inline $ t \ in (0,1) $ inline $ , pour nos besoins, les chiffres dans la zone sont les mieux adaptés
$ inline $ 1- \ mathrm {const} / \ sqrt {n} $ inline $ . Pour chacun
$ inline $ k = 1,2, \ ldots $ inline $
considérer la distribution géométrique sur des entiers non négatifs avec une moyenne
$ en ligne $ t ^ k $ en ligne $ (c.-à-d. probabilité du nombre
$ inline $ m = 0,1, \ ldots $ inline $ est égal à
$ en ligne $ t ^ {km} (1-t ^ k) $ en ligne $ ) On choisit selon elle une variable aléatoire
$ inline $ m_k $ inline $ (il existe de nombreuses façons d'organiser cela). En général
$ en ligne $ k $ en ligne $ très probablement 0. Regardons le diagramme de Young dans lequel
$ inline $ m_k $ inline $ les lignes sont de longueur
$ en ligne $ k $ en ligne $ à chaque
$ inline $ k = 1,2, \ ldots $ inline $ . Je l'appelle
la méthode du navire, car la superficie totale est
parfois égale à
$ en ligne $ n $ en ligne $ . Si ce n'est pas égal, répétez l'expérience. En fait égal
$ en ligne $ n $ en ligne $ elle assez souvent si elle choisit intelligemment
$ inline $ t \ in (0,1) $ inline $ . J'invite le lecteur à prouver indépendamment que tous les diagrammes d'une zone donnée sont également probables et à estimer le nombre d'étapes.