29 mars 2019 - Michael Trott, chercheur principal
Entrée
Dans le soi-disant «nouveau SI» - une
version mise à jour du Système international d'unités , qui déterminera sept unités de mesure de base (seconde, mètre, kilogramme, ampère, kelvin, mole et candela) et qui entrera en vigueur le 20 mai 2019, toutes les unités SI seront déterminé par les valeurs exactes des constantes physiques fondamentales. En conséquence, toutes les unités SI ci-dessus (Newton, Volt, Ohm, Pascal, etc.) seront finalement exprimées en termes de constantes fondamentales. (Enfin, la physique fondamentale contrôlera littéralement notre vie quotidienne ☺)
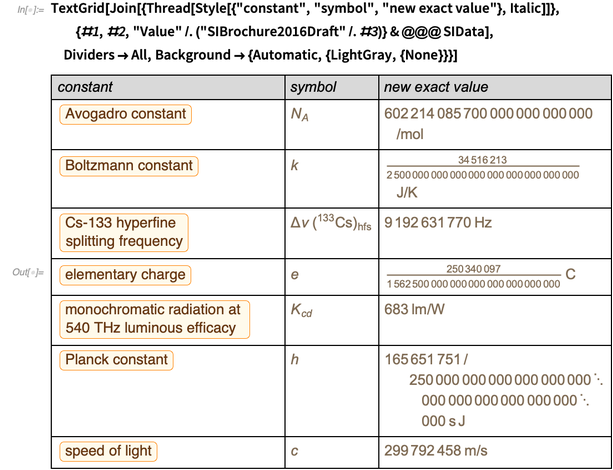
Le tableau ci-dessous montre comment tout va changer du lundi soir 20 mai au mardi matin 21 mai de cette année.
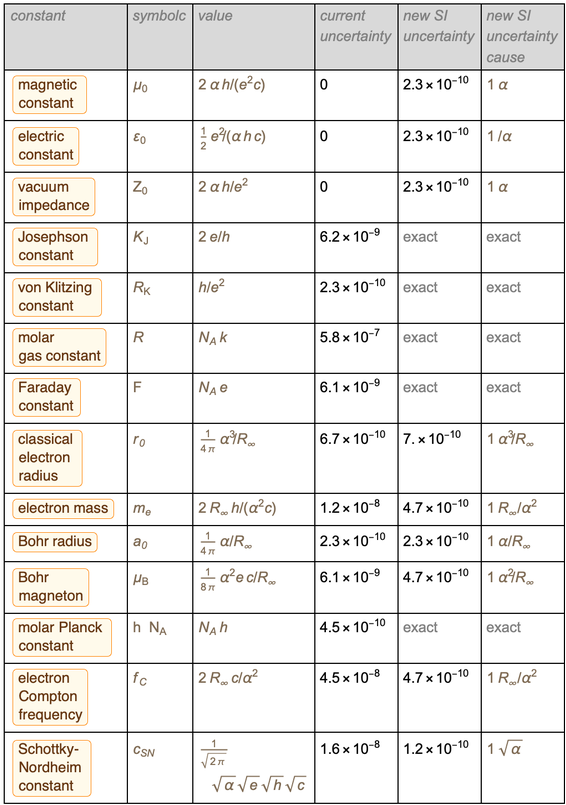
Le calcul des données de ce tableau est l'objectif de ce blog. Commençons donc par un bref aperçu de ce qui va changer dans le nouveau SI.
En plus de la valeur exacte bien connue de la vitesse de la lumière, en quatre semaines, quatre autres constantes physiques - la constante de Planck, la constante de Boltzmann, la constante d'Avogadro et la constante de Millikan (souvent appelée la charge électrique élémentaire) - auront des valeurs exactes. La décision sur ce changement a été prise au niveau international en novembre de l’année dernière (j’en ai parlé dans ma dernière
blog).
Vous trouverez ci-dessous un extrait de la page 12 du projet de
brochure SI en cours .
Notez que dans ces définitions, les nombres décimaux sont considérés comme des nombres décimaux exacts, pas, par exemple, des numéros de machine sur un ordinateur qui ont une précision finie et ne sont pas des nombres exacts. La fréquence de transition dans la structure superfine divisée du Cs-133, la vitesse de la lumière et «l'efficacité lumineuse» ont déjà des valeurs exactes aujourd'hui.
Le monde discute des changements futurs
Ce changement aura des conséquences intéressantes pour d'autres constantes physiques: certaines constantes qui sont actuellement mesurées et qui ont des erreurs deviendront précises, et certaines constantes qui sont actuellement précises auront des valeurs approximatives avec des erreurs finies à l'avenir . Ces modifications sont inévitables pour garantir la cohérence globale du système.
Le premier numéro
de Physics of the World de cette année a abordé ce sujet dans une
lettre à l'éditeur de William Hough; il a écrit:
Avec la fixation de la charge sur l'électron ( e ) et la constante de Planck ( h ), toutes les unités physiques sont désormais «immortalisées dans la pierre», ce qui est très agréable. Mais cela soulève une question délicate. Constante de structure fine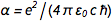 
où c est la vitesse de la lumière et 
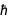c'est 
. Des équations familières 
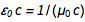et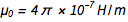 
nous constatons rapidement que 
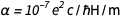. Ceci, bien sûr, est un nombre pur avec une quantité sans dimension, et il est maintenant fixé pour toujours comme égal à 1 / 137.13601, ce qui est très proche de la valeur acceptée. Cela n'est pas surprenant, car cette dernière valeur serait utilisée dans les nouvelles valeurs convenues pour e et ℏ . Mais la nature a sa propre valeur, inconnue de nous actuellement, qui, de ce fait, est immortalisée dans le diamant. Nous pouvons être pardonnés d'avoir laissé entendre que nous connaissons mieux que la nature. Mais que faire si la future théorie de l'univers est acceptée et donne le sens exact 
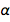Laquelle est significativement différente de la valeur acceptée? Cela pourrait-il arriver? Il y a eu des tentatives pour trouver une valeur théorique pour α , mais elles incluent l'électrodynamique quantique menaçante et controversée.
Le problème est que dans le nouveau système SI,
et
aura désormais des valeurs inexactes avec une erreur. Dans ce blog, nous utiliserons le Wolfram Language et sa connaissance des unités physiques et des constantes pour voir comment ces constantes physiques et d'autres gagnent (ou perdent) des erreurs, et pourquoi il s'agit d'une conséquence mathématique de la définition des unités de base.
Un bref aperçu de la langue Wolfram
Wolfram Language est un support unique pour mener des expériences numériques et des calculs symboliques, identifier les conséquences possibles. En plus des capacités informatiques générales, trois composants système sont très utiles ici:
1) Wolfram Language units et structure des grandeurs physiques.
Les unités classiques (comme les mètres, les pieds, etc.) peuvent être utilisées dans les calculs et les visualisations. Et, bien sûr, dans la conversion des unités de mesure.
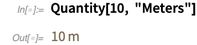
La conversion en unités américaines ordinaires entraîne une fraction (plutôt qu'une valeur approximative du nombre réel!) En raison des ratios bien définis des deux unités.
Les physiciens aiment (surtout) utiliser des unités "naturelles". Souvent, ces unités naturelles ne sont que des constantes physiques ou des combinaisons de celles-ci. Par exemple, la vitesse de la lumière (la saisie en langage naturel est utilisée ici).
Exprimée en unités SI (car il s'agit de la vitesse et des unités en mètres et en secondes sont nécessaires), la vitesse de la lumière a une valeur précise.
En revanche, la constante de Planck n'a actuellement pas de valeur exacte. Ainsi, sa valeur, exprimée en unités de base SI, est un nombre décimal approximatif.
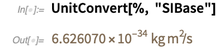
Veuillez noter que la précision de 6,626070 ... reflète le nombre de nombres connus.
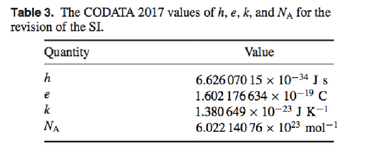
Il s'agit de la dernière valeur recommandée pour la constante de Planck publiée dans
CODATA 2017 en préparation du raffinement des constantes. Voici le tableau correspondant:
Les constantes physiques (ou leurs combinaisons) qui relient deux quantités physiques peuvent souvent être utilisées comme unités naturelles. Les exemples les plus simples seraient la mesure de la vitesse en termes de vitesse de la lumière ou le couple microscopique en termes de
ℏ . Ou l'énergie peut être mesurée en termes de masse avec un facteur implicite
. La fonction
DimensionalCombinations peut être utilisée pour rechercher des combinaisons de constantes physiques qui vous permettent de relier deux quantités physiques données. Par exemple, les relations suivantes entre la masse et l'énergie peuvent être établies:
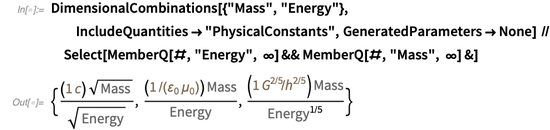
La première égalité reflète la célèbre formule d'Einstein
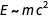
, la seconde est l'équivalent de la première relation, et la troisième - (dimensionnellement) déclare que
.
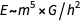
2) La classe d'entité «
PhysicalConstant » a récemment été ajoutée à la base de
connaissances Wolfram .
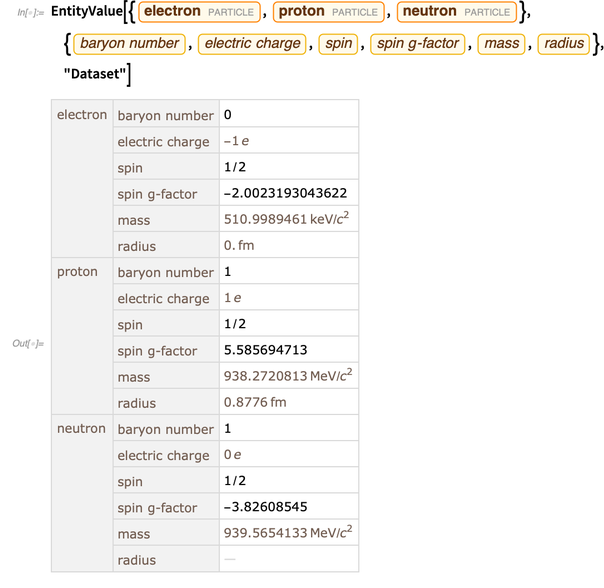
Les fonctions et les objets du Wolfram Language naissent «par le calcul», c'est-à-dire qu'ils sont prêts à être utilisés en informatique. Mais pour décrire et simuler le monde réel, vous avez besoin de données sur le monde réel. La structure d'entité est un moyen pratique et entièrement intégré d'obtenir de telles données. Voici quelques données sur l'électron, le proton et le neutron.
L'une des nouvelles unités d'entité est les constantes physiques. Actuellement, la base de connaissances contient plus de 250 constantes physiques.
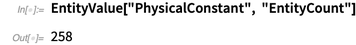
Voici une douzaine d'exemples choisis au hasard. De plus, sans une définition claire de quelles constantes sont des constantes physiques, des masses de particules fondamentales, des paramètres de Lagrange du modèle standard, etc. Pour plus de commodité, la liste contient également des
constantes astronomiques conformément à l'Almanach astronomique.
La plupart des constantes physiques fondamentales étaient appelées constantes de classe C dans le célèbre
ouvrage de Jean-Marc Levy-Leblond. Les constantes suivantes sont des classes C et B.
Prenons, par exemple, l'unité de temps naturelle, le temps de Planck. Les fonctions
ToEntity et
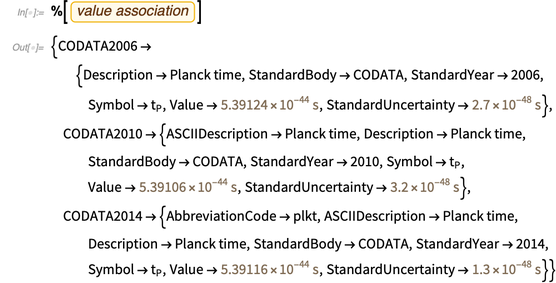
FromEntity facilitent le va-et-vient entre les constantes physiques en tant qu'unités et les constantes physiques en tant qu'entités. Une entité correspondant à une unité de temps de Planck est présentée ci-dessous.
La base de connaissances contient de nombreuses méta-informations le concernant, par exemple ses valeurs dans les dernières listes CODATA.
La dernière conclusion, qui contient du sens et de l'erreur, nous amène à la troisième fonction importante, qui sera utile plus tard:
3) Introduction de la fonction
Around [] dans la version 12 de Wolfram Language. La fonction
Around [] fournit une valeur inexacte, indiquant la valeur moyenne et l'erreur. Le modèle arithmétique
Around [] est basé sur le
GUM (Guide to Expressing Measurement Error) - à ne pas confondre avec le Leibniz Plus-Minus-calculus. Voici une telle valeur avec une erreur.
L'aspect le plus important et utile du calcul avec des valeurs qui comportent des erreurs est qu'elles tiennent compte des corrélations. L'utilisation naïve de telles valeurs dans les nombres ou intervalles arithmétiques peut sous-estimer ou surestimer l'erreur résultante.
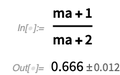
Ci-dessous, nous voyons que la fonction
AroundReplace [] prend en compte la corrélation.
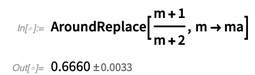
Retour à la lettre à l'éditeur
Utilisons maintenant ces trois composants et la lettre plus détaillée de William Hough à l'éditeur.
Aux valeurs approximatives actuelles de
e et
ℏ , ces deux valeurs pour la constante de structure fine sont cohérentes dans les limites de leurs erreurs. La première est l'expression de la lettre à l'éditeur et la seconde est la quantité (
Quantité []), qui représente la constante de structure fine.
Toutes les quelques années, CODATA publie les valeurs officielles des constantes fondamentales (voir
constantes de structure fine ); comme je l'ai dit, les valeurs utilisées dans le Wolfram Language sont les dernières valeurs CODATA et l'erreur finale se reflète dans la précision du nombre.
Veuillez noter que la constante de structure fine directement mesurée est légèrement plus précise que celle qui exprime la constante de structure fine à travers d'autres constantes.
Si nous utilisons les valeurs exactes à venir de
e et
ℏ ,
et utilisons la valeur exacte actuelle
, nous obtenons la valeur exacte suivante pour la constante de structure fine sous la forme
.
Il est peu probable que le Seigneur, qui ne
joue même pas
aux dés , choisisse un tel nombre pour la valeur
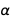
dans notre univers. Cela signifie que si
e et
ℏ sont fixes dans le nouveau SI, les valeurs exactes actuelles
et
doit être inévitablement «découplé» (voir aussi l'
article de Goldfarb sur la quantité
nouveau SI). (Nous reviendrons sur pourquoi
et
bientôt inexact.)
Cela signifie qu'après le 20 mai de cette année, ces résultats seront différents de ceux donnés ci-dessous.
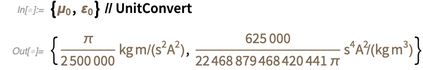
(Dans une brève note, la classe d'entité "
PhysicalConstant " a également des valeurs estimées pour les constantes, telles que la constante de structure fine):
Maintenant, en dehors de l'argument théologique sur la forme exacte de la constante de structure fine, d'un point de vue physique, pourquoi
et
devrait être inexact? Comme argument de probabilité, considérons
. L'un des résultats les plus remarquables est la loi de Coulomb.
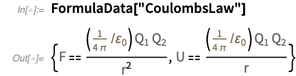
Dans le
système SI
existant , les ampères ont une définition «exacte»:
Un ampère est ce courant continu qui, s'il est supporté par deux conducteurs parallèles de longueur infinie avec une légère section ronde et placé à une distance de 1 mètre dans le vide, va créer une force entre ces conducteurs égale à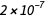 
Newton par mètre de longueur. Cette définition utilise des quantités purement mécaniques Newton et mètre (c'est-à-dire, après expansion, il s'agit d'un second, mètre et kilogramme). Aucune relation n'est établie avec la charge de l'électron, et dans le système SI existant, la charge élémentaire est une quantité mesurée expérimentalement.
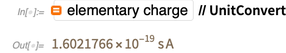
Et cette valeur mesurée expérimentalement a changé au fil des ans, devenant plus précise.
La force sur le côté gauche de la loi de Coulomb (exprimée en Newtons) contient l'unité de base du kilogramme, qui, après que la valeur de la constante de Planck soit constante, devient également précisément définissable. Puisqu'il n'y a aucune raison de croire que toutes les lois de la nature peuvent être exprimées en nombres rationnels finis, la seule «partie mobile» possible dans la loi de Coulomb sera
. Sa valeur numérique doit être déterminée, et elle fera coïncider les côtés gauche et droit de la loi de Coulomb.
D'un point de vue plus fondamental de la physique, la constante de structure fine est la constante d'interaction, qui détermine la force des interactions électromagnétiques. Et, peut-être un jour, la physique pourra calculer la valeur de la constante de structure fine, mais nous en sommes encore loin. Le simple choix des définitions d'unité ne peut pas fixer la valeur
.
Sont tous les deux vraiment
et
devenir non fixé, ou est-il possible de garder l'un d'eux précis? En raison de la vitesse de la lumière déjà précise et du rapport
si l'un des
ou
précis, l'autre doit également être précis. Nous savons qu'au moins un doit devenir non engagé, il s'ensuit que les deux doivent être non engagés.
Les valeurs qui sont maintenant données par la constante de Planck, la constante de Boltzmann, la constante d'Avogadro et la charge élémentaire ne sont ni arbitraires ni entièrement définies. Ils sont déterminés jusqu'à huit caractères environ, de sorte que les unités de mesure qu'ils déterminent après le 20 mai correspondent à la "taille" des unités qu'ils déterminent avant le 20 mai. Mais les chiffres en bas à droite ne sont pas définis. Ainsi, la valeur de la valeur exacte future de la charge élémentaire peut être
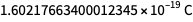
mais pas
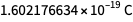
. C'est le rasoir et la rationalité d'Occam qui nous permettent d'utiliser
.
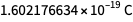
Sur un plan plus technique, la substitution dans le calcul précédent était que par le terme
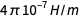
dans la formule
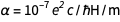l'ampli a été utilisé avant la redéfinition (rappelez-vous
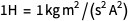
), mais la valeur exacte de la charge élémentaire a également été utilisée, c'est-à-dire la définition de l'ampère après redéfinition. Et nous devons toujours rester dans un seul système d'unités.
Calcul d'une table de formulaire optimisée pour les erreurs
Alors, la question naturelle se pose: quelles devraient être ces significations «non fixées»? Dans mon dernier blog, j'ai créé manuellement une nouvelle valeur
. Ce qui peut être fait manuellement peut être fait à l'aide d'un programme informatique, alors implémentons un petit programme qui calcule la forme optimisée en termes d'erreurs des dérivées des constantes physiques. Dans une approche prospective, une classe d'entité de sept constantes qui définit un nouveau SI est déjà disponible.
Voici les constantes qui auront une valeur exacte dans le nouveau SI.
Les valeurs actuelles de ces constantes ainsi que leur erreur (calculées à l'aide de la fonction
Around []) ont la forme:
En utilisant la classe d'entité «
PhysicalConstant », nous pouvons obtenir de nouvelles valeurs à venir de quantités physiques. Notez que, comme dans tous les langages informatiques, les entiers exacts et les nombres rationnels sont soit des entiers explicites soit des nombres rationnels (mais pas décimaux).
De nombreuses constantes physiques peuvent être reliées par des équations données par les théories physiques de divers domaines de la physique. A l'avenir, nous voulons nous limiter à la théorie des phénomènes électromagnétiques fondamentaux, dans laquelle l'erreur des constantes sera réduite à l'erreur de la constante de structure fine
et constante de Rydberg
. Si nous incluions, par exemple, les phénomènes gravitationnels, nous aurions à utiliser la constante gravitationnelle G, qui est mesurée indépendamment, bien qu'elle présente une très grande erreur (c'est pourquoi la NSF avait le soi-disant «
Big-G Challenge »).
De plus, nous nous limitons aux quantités électriques, magnétiques et de masse, dont les erreurs sont réduites à des unités
et
.
Ci-dessous, nous utilisons la nouvelle fonction
Around pour exprimer des valeurs avec des erreurs correspondantes
et
.
Actuellement, selon CODATA 2014, l'erreur relative pour
est sur le point
, et pour
à propos
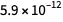
. Comme vous pouvez le voir, l'erreur de
plus que pour
.
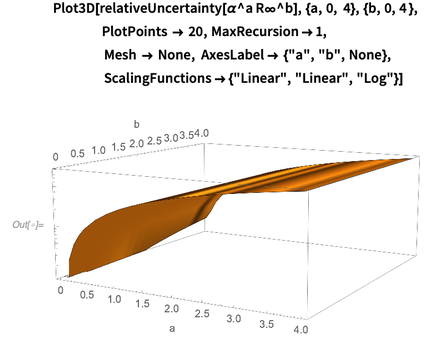
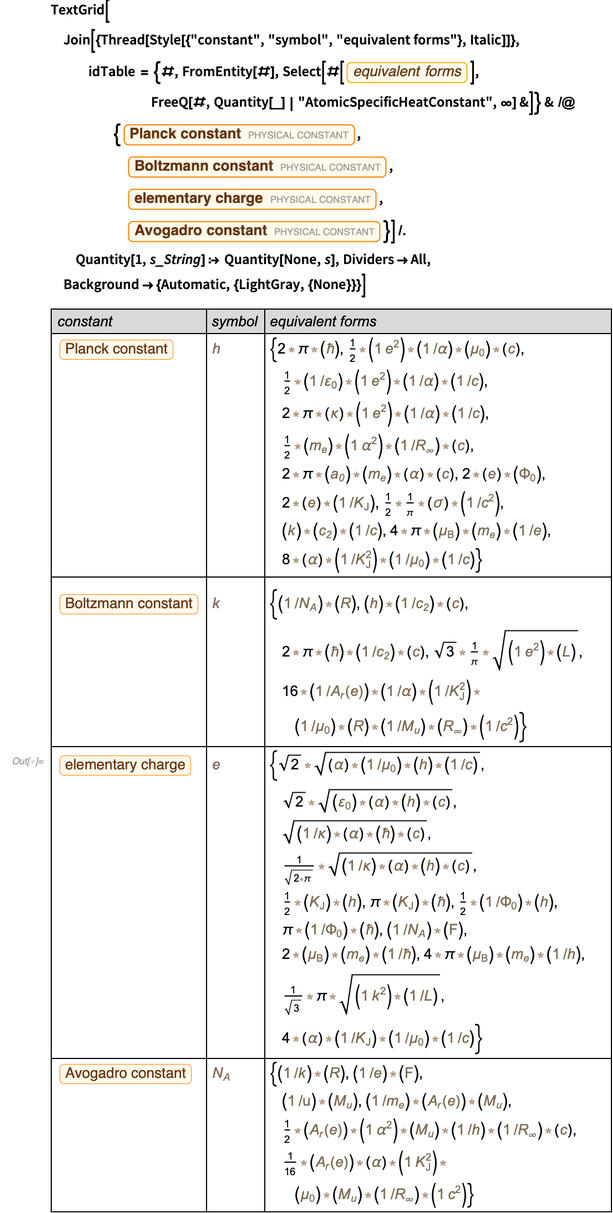
Voici un graphique de l'erreur relative log-base-10
comme fonctions
a et
b . Évidemment, pour de petits degrés, l'erreur relative du produit dépend faiblement des exposants
a et
b . Ce graphique montre que la dépendance de l'erreur
domine par rapport à
a (exposant de structure fine). Cette observation s'explique par le fait que l'erreur de la constante de Rydberg est 50 fois inférieure à l'erreur de la constante de structure fine.
Pour calculer les erreurs de différentes constantes dans le nouveau SI, nous utiliserons les étapes suivantes:
• Récupération de représentations équivalentes pour les constantes physiques accessibles à partir de la classe d'entités
PhysicalConstant .
Ces égalités identiques entre les constantes physiques sont les lois de la physique et en tant que telles doivent être préservées à la fois dans l'ancien et le nouveau SI.
• Considérez les formules comme un ensemble d'égalités algébriques auxquelles différentes méthodes d'exclusion peuvent être appliquées pour exprimer une constante à travers une combinaison de sept constantes de base du nouveau SI, ainsi que des constantes de structure fine
et les constantes de Rydberg
.
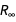
Ce sont les neuf constantes de base que nous permettons d'appliquer dans les définitions de chaque nouvelle constante considérée. (Techniquement, il y a 10 constantes dans la liste, mais en raison de la simple relation d'échelle entre
h et
ℏ , il y a en fait neuf constantes «différentes» dans cette liste.)
La classe d'entité «
PhysicalConstant » contient beaucoup d'informations sur les relations entre les constantes physiques. Par exemple, voici des formes équivalentes de quatre constantes qui sont actuellement mesurées et qui seront bientôt identifiées comme ayant des valeurs précises.
Dans la précision des valeurs mesurées, tous ces éléments unitaires fonctionnent maintenant. Voici une vérification numérique rapide des formes alternatives de la constante de Planck. Mais la valeur numérique spécifique, en particulier l'erreur, dépend de la forme réelle de présentation.
Around [], .
. .
, . , ? , , , , , .
, , ( ,
Entité [" PhysicalConstant",. ] et en quantité [ 1 ,. ] sont assimilés). La raison pour laquelle nous utilisons des entités, plutôt que des quantités dans les calculs ultérieurs, est double: premièrement, les entités sont des représentations pratiques et faciles à lire; et deuxièmement, les fonctions algébriques (telles que GroebnerBasis ) ne pénètrent pas les quantités pour déterminer la nature de leur premier argument.
Ensuite, nous rendons toutes les identités polynomiales. La dernière étape signifie: (1) soustraire le côté gauche du côté droit; et (2) qu'aucun pouvoir fractionnaire (par exemple, racines carrées) des constantes n'apparaît plus. Nous effectuons une telle transformation en polynôme en recherchant tous les exposants fractionnaires et en trouvant le LCM (plus petit facteur commun) de tous leurs dénominateurs.
Voici une des équations précédentes qui contient des constantes avec une puissance fractionnaire.
Après polynomialisation, on arrive aux polynômes de plusieurs variables dans les trois constantes présentes. Ces polynômes doivent être éliminés.
Le tableau suivant montre comment la fonction
toPolynomial s'applique aux formes équivalentes présentées précédemment pour une charge élémentaire. Après la canonisation de ℏ en
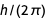
, certains des polynômes résultants deviennent identiques.
Maintenant, sur la base des constantes physiques disponibles (sans les constantes utilisées pour déterminer le nouveau SI), nous obtenons suffisamment de formes équivalentes pour créer un ensemble d'équations.
Voici une liste des équations polynomiales obtenues pour l'expression d'une charge élémentaire.
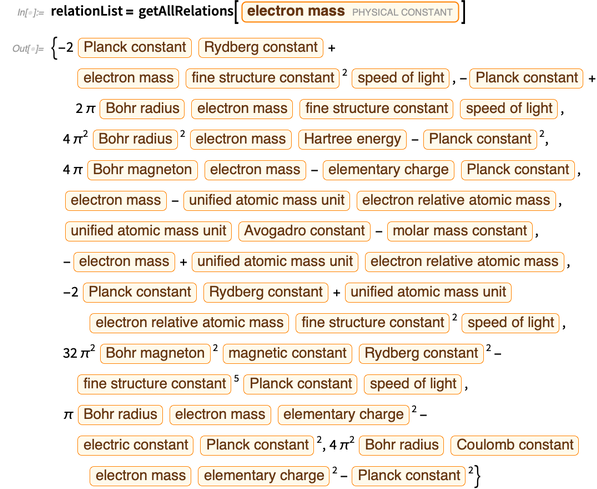
Nous exprimons toutes les erreurs à travers les erreurs
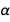
et
. Seules ces deux constantes suffisent à exprimer l'erreur de nombreuses constantes physiques. Et puisque leurs erreurs sont indépendantes l'une de l'autre, et comme les erreurs sont assez petites, ces deux constantes assez bien connues sont les mieux adaptées pour exprimer une nouvelle version optimisée (au sens d'erreurs) de nombreuses constantes physiques. Et, bien sûr, nous autorisons les sept constantes exactes du nouveau SI; comme ce sont des quantités précises, leur présence ne changera pas l'erreur.
Les principaux travaux sur l'expression d'une constante donnée en termes de constantes SI et
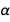
et
sera implémenté par la fonction
GroebnerBasis . La définition du paramètre
MonomialOrder -> ElventionOrder est une étape critique qui supprime toutes les quantités physiques «inutiles», laissant une équation polynomiale avec des constantes définies avec précision et (si nécessaire) une structure fine et des constantes Rydberg.
En éliminant les constantes liées par la masse de l'électron, on obtient
.
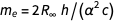
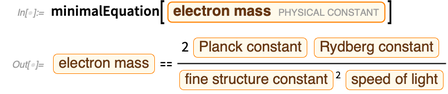
L'erreur de cette expression provient du terme
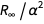
. Nous pouvons définir une fonction qui supprime un membre
provoquant une erreur.
Pour une représentation plus compacte, nous pouvons définir une fonction qui renvoie une forme équivalente, ainsi que des erreurs anciennes et nouvelles - sous la forme d'une chaîne.
Nous terminons le blog avec un tableau des erreurs anciennes et nouvelles pour plus d'une douzaine de constantes physiques. Cette liste est sélectionnée comme exemple représentatif; d'autres constantes peuvent être traitées de la même manière (cela peut nécessiter l'ajout de constantes imprécises supplémentaires pour la conservation, telles que la constante gravitationnelle ou les paramètres du modèle standard).
La combinaison des lignes dans un tableau donne le résultat suivant pour la représentation optimale de ces constantes dans le nouveau système d'unités SI.
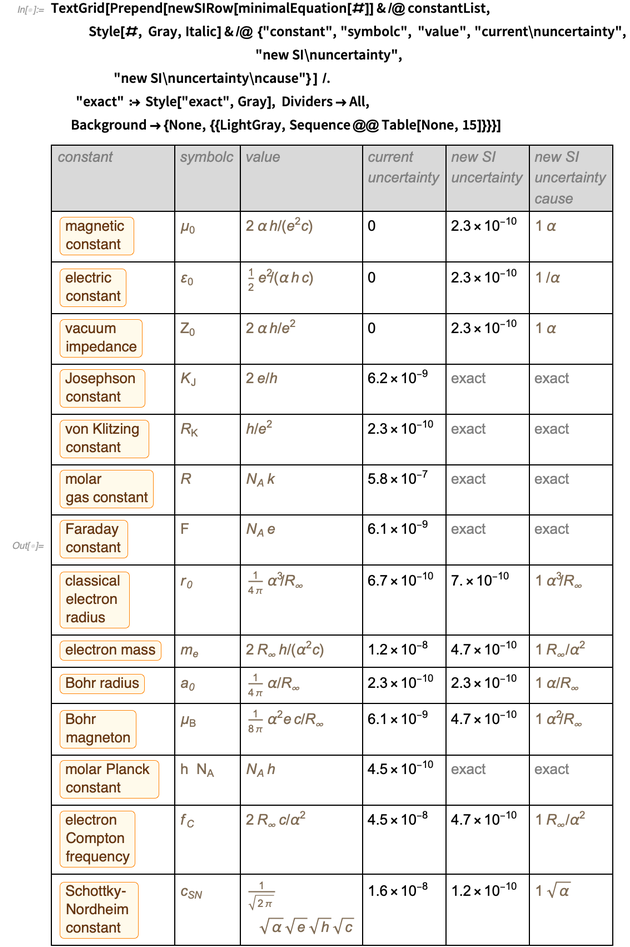
C'était une table que nous avions l'intention d'afficher, et nous avons réussi à l'afficher. Faites attention à l'apparence
au numérateur et au dénominateur
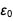
et
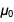
de sorte qu'après réduction du résultat
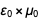
devient
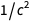
. Une liste similaire se trouve au bas de la page Wikipedia sur la
redéfinition des unités SI .
Nous pouvons maintenant nous attendre calmement à
la Journée mondiale de la métrologie 2019 pour un monde fondamentalement meilleur, décrit par des constantes fondamentales.
Téléchargez le blog
Wolfram Notebook .
Système Wolfram Mathematica temporaire gratuitVous avez une question? Contactez info-russia@wolfram.com