🖌️ 🆒 👩‍👩‍👧‍👧 Analyse des ondelettes, partie 1 👵🏽 👋🏿 📵

Présentation

Considérons la transformée en ondelettes discrètes (DWT) implémentée dans la bibliothèque PyWavelets PyWavelets 1.0.3 . PyWavelets est un logiciel gratuit et open source publié sous la licence MIT.

Lors du traitement de données sur un ordinateur, une version discrétisée de la transformée en ondelettes continue peut être effectuée, dont les bases sont décrites dans mon article précédent. Cependant, la spécification de valeurs discrètes des paramètres (a, b) d'ondelettes avec une étape arbitraire Δa et Δb nécessite un grand nombre de calculs.

De plus, il en résulte un nombre excessif de coefficients, dépassant de loin le nombre d'échantillons du signal d'origine, ce qui n'est pas nécessaire à sa reconstruction.

La transformée en ondelettes discrètes (DWT) implémentée dans la bibliothèque PyWavelets fournit suffisamment d'informations tant pour l'analyse du signal que pour sa synthèse, tout en étant économique en termes de nombre d'opérations et de mémoire requise.

Quand utiliser la transformée en ondelettes au lieu de la transformée de Fourier

La transformée de Fourier fonctionnera très bien lorsque le spectre de fréquences est stationnaire. Dans ce cas, les fréquences présentes dans le signal sont indépendantes du temps et le signal contient les fréquences xHz qui sont présentes n'importe où dans le signal. Plus le signal est instable, plus les résultats sont mauvais. C'est un problème, car la plupart des signaux que nous voyons dans la vie réelle sont de nature instable.

La transformée de Fourier a une résolution élevée dans le domaine fréquentiel, mais une résolution nulle dans le domaine temporel. Nous le montrons dans les deux exemples suivants.

Annonce

import numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt # 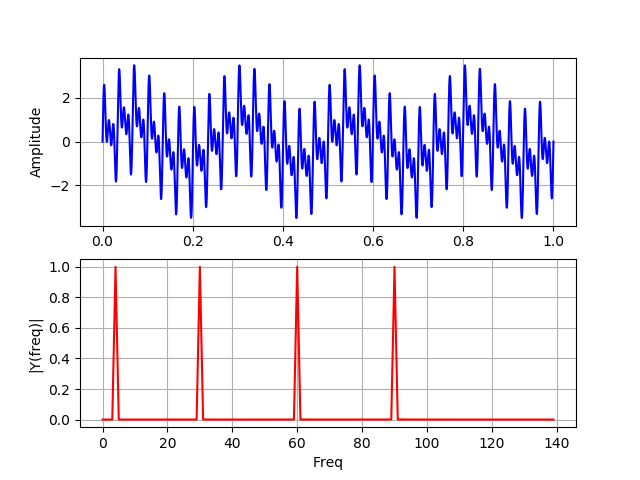sampling rate, Fs = 0,1 MHz n = len(y) # length of the signal k = np.arange(n) T = n / Fs frq = k / T # two sides frequency range frq = frq[range(n // 2)] # one side frequency range Y = fftpack.fft(y) / n # fft computing and normalization Y = Y[range(n // 2)] / max(Y[range(n // 2)]) # plotting the data subplot(2, 1, 1) plot(k/N , y, 'b') ylabel('Amplitude') grid() # plotting the spectrum subplot(2, 1, 2) plot(frq[0:140], abs(Y[0:140]), 'r') xlabel('Freq') plt.ylabel('|Y(freq)|') grid() y= y1a + y2a + y3a + y4a spectrum_wavelet(y) show()

Sur ce graphique, les quatre fréquences sont présentes dans le signal pendant toute la durée de son fonctionnement.

Annonce

 import numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt # 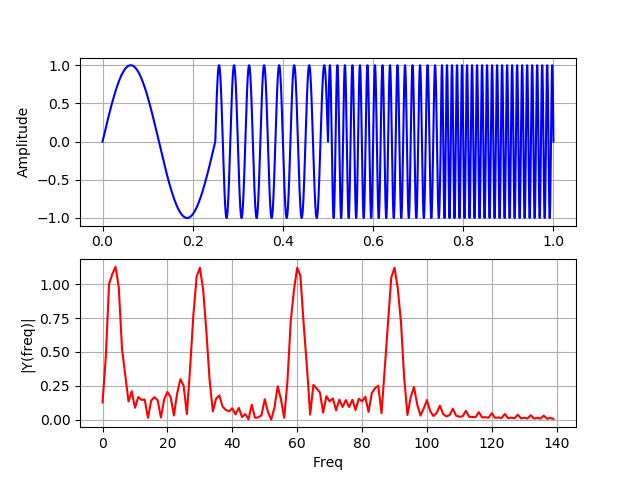sampling rate, Fs = 0,1 MHz n = len(y) # length of the signal k = np.arange(n) T = n / Fs frq = k / T # two sides frequency range frq = frq[range(n // 2)] # one side frequency range Y = fftpack.fft(y) / n # fft computing and normalization Y = Y[range(n // 2)] / max(Y[range(n // 2)]) # plotting the data subplot(2, 1, 1) plot(k/N , y, 'b') ylabel('Amplitude') grid() # plotting the spectrum subplot(2, 1, 2) plot(frq[0:140], abs(Y[0:140]), 'r') xlabel('Freq') plt.ylabel('|Y(freq)|') grid() y = np.concatenate([y1b, y2b, y3b, y4b]) spectrum_wavelet(y) show()

Sur ce graphique, les signaux ne se chevauchent pas dans le temps, les lobes latéraux sont dus à un écart entre quatre fréquences différentes.

Pour deux spectres de fréquence contenant exactement les mêmes quatre pics, la transformée de Fourier ne peut pas déterminer où ces fréquences sont présentes dans le signal. La meilleure approche pour analyser des signaux avec un spectre de fréquence dynamique est la transformée en ondelettes.

Les principales propriétés des ondelettes

Le choix du type, et donc des propriétés de l'ondelette, dépend de la tâche d'analyse, par exemple, pour déterminer les valeurs efficaces des courants dans l'industrie électrique, les formes d'onde d'ordre supérieur d'Ingrid Daubechies offrent une plus grande précision. Les propriétés des ondelettes peuvent être obtenues à l'aide de la fonction pywt.DiscreteContinuousWavelet () dans la liste suivante:

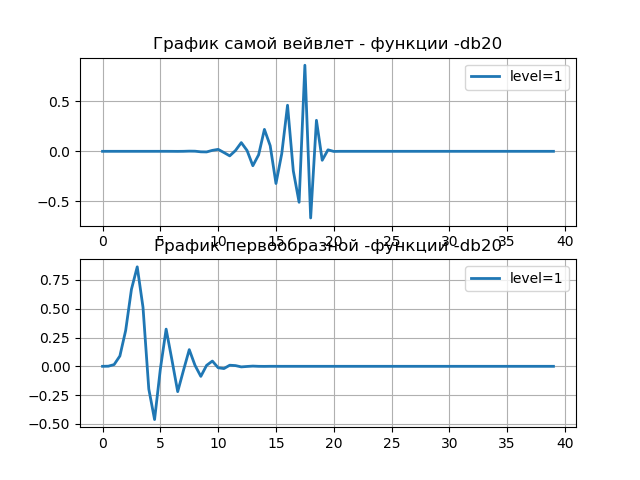
Annonce

 import pywt from pylab import * from numpy import * discrete_wavelets = ['db5', 'sym5', 'coif5', 'haar'] print('discrete_wavelets-%s'%discrete_wavelets ) st='db20' wavelet = pywt.DiscreteContinuousWavelet(st) print(wavelet) i=1 phi, psi, x = wavelet.wavefun(level=i) subplot(2, 1, 1) title("   -  -%s"%st) plot(x,psi,linewidth=2, label='level=%s'%i) grid() legend(loc='best') subplot(2, 1, 2) title("  - -%s"%st) plt.plot(x,phi,linewidth=2, label='level=%s'%i) legend(loc='best') grid() show()

Nous obtenons:

discrete_wavelets - ['db5', 'sym5', 'coif5', 'haar']

 Wavelet db20 Family name: Daubechies Short name: db Filters length: 40 Orthogonal: True Biorthogonal: True Symmetry: asymmetric DWT: True CWT: False

Dans un certain nombre de cas pratiques, il est nécessaire d'obtenir des informations sur la fréquence centrale de l'ondelette psi - une fonction qui est utilisée, par exemple, dans l'analyse en ondelettes des signaux pour détecter les défauts des engrenages:

 import pywt f=pywt.central_frequency('haar', precision=8 ) print(f) #  : scale=1 f1=pywt.scale2frequency('haar',scale) print(f1)

 0.9961089494163424 0.9961089494163424

Utilisation de la fréquence centrale

f_{c}

$f_ {c}$ l'ondelette maternelle et le facteur d'échelle «a» peuvent convertir les échelles en pseudo-fréquences

f_{a}

$f_ {a}$ en utilisant l'équation:

f_{a} = f r a c f_{c} a

$f_ {a} = \ frac {f_ {c}} {a}$

Modes d'extension du signal

Avant de calculer la transformée en ondelettes discrète à l'aide de bancs de filtres , il devient nécessaire d' allonger le signal . Selon la méthode d'extrapolation, des artefacts importants peuvent se produire aux limites du signal, entraînant des inexactitudes dans la transformation DWT.

PyWavelets fournit plusieurs techniques d'extrapolation de signal qui peuvent être utilisées pour minimiser cet effet négatif. Pour illustrer ces méthodes, utilisez la liste suivante:

Liste de démonstration des méthodes d'extension de signal

 import numpy as np from matplotlib import pyplot as plt from pywt._doc_utils import boundary_mode_subplot # synthetic test signal x = 5 - np.linspace(-1.9, 1.1, 9)**2 # Create a figure with one subplots per boundary mode fig, axes = plt.subplots(3, 3, figsize=(10, 6)) plt.subplots_adjust(hspace=0.5) axes = axes.ravel() boundary_mode_subplot(x, 'symmetric', axes[0], symw=False) boundary_mode_subplot(x, 'reflect', axes[1], symw=True) boundary_mode_subplot(x, 'periodic', axes[2], symw=False) boundary_mode_subplot(x, 'antisymmetric', axes[3], symw=False) boundary_mode_subplot(x, 'antireflect', axes[4], symw=True) boundary_mode_subplot(x, 'periodization', axes[5], symw=False) boundary_mode_subplot(x, 'smooth', axes[6], symw=False) boundary_mode_subplot(x, 'constant', axes[7], symw=False) boundary_mode_subplot(x, 'zeros', axes[8], symw=False) plt.show()

Les graphiques montrent comment un signal court (rouge) se dilate (noir) au-delà de sa longueur d'origine.

Transformation en ondelettes discrète

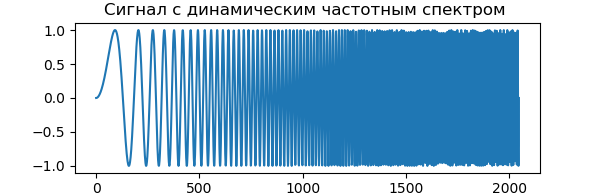
Pour démontrer DWT, nous utiliserons un signal avec un spectre de fréquence dynamique, qui augmente avec le temps. Le début du signal contient des valeurs de basse fréquence et la fin du signal contient des fréquences de la gamme des ondes courtes. Cela nous permet de déterminer facilement quelle partie du spectre de fréquences est filtrée en regardant simplement l'axe du temps:

Annonce

 from pylab import * from numpy import* x = linspace(0, 1, num=2048) chirp_signal = sin(250 * pi * x**2) fig, ax = subplots(figsize=(6,1)) ax.set_title("     ") ax.plot(chirp_signal) show()

La transformée en ondelettes discrète dans PyWavelets 1.0.3 est la fonction pywt.dwt (), qui calcule les coefficients approximatifs cA et les coefficients détaillés cD de la transformée en ondelettes de premier niveau du signal spécifié par le vecteur:

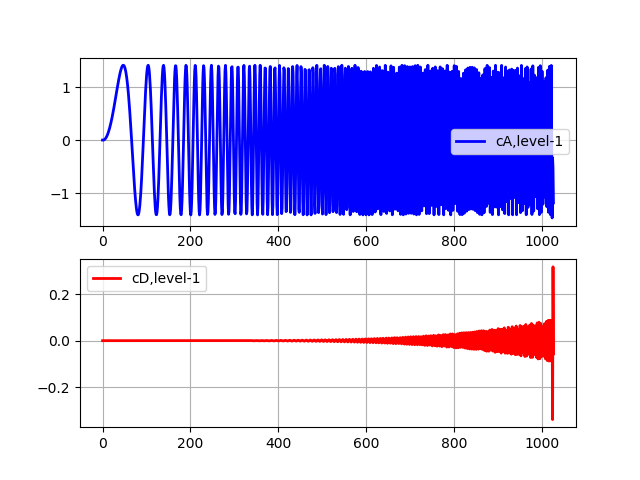
Inscription au niveau de transformation 1

 import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-1') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-1') grid() legend(loc='best') show()

Liste de transformation niveau 5

 import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show()

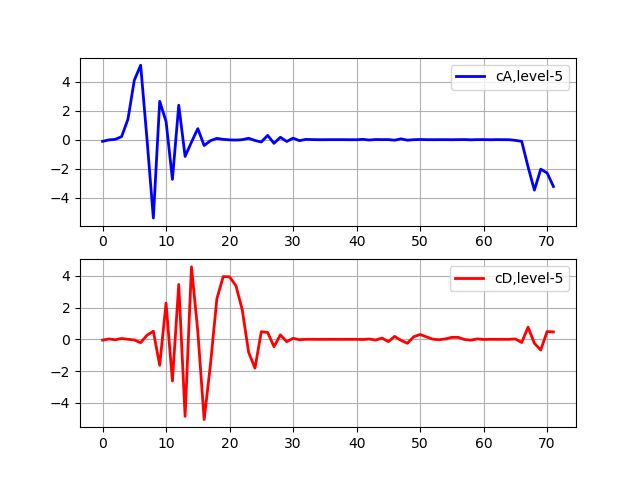
Les coefficients d'approximation (cA) représentent la sortie du filtre passe-bas (filtre de moyenne) DWT. Les coefficients de détail (cD) représentent la sortie du filtre passe-haut (filtre différentiel) DWT.

Vous pouvez utiliser la fonction pywt.wavedec () pour calculer immédiatement les coefficients de niveau supérieur. Cette fonction prend le signal d'entrée et le niveau en entrée et renvoie un ensemble de coefficients d'approximation (n-ième niveau) et n ensembles de coefficients de détail (de 1 à n-ième niveau). Voici un exemple pour le cinquième niveau:

 from pywt import wavedec from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=5) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show()

En conséquence, nous obtenons les mêmes graphiques que dans l'exemple précédent. Les coefficients cA et cD peuvent être obtenus séparément:

Pour cA:

 import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('a', data, 'db20', mode='symmetric', level=1)

Pour cD:

 import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('d', data, 'db20', mode='symmetric', level=1)

Banque de filtres

Certains des problèmes liés aux niveaux de conversion ont été abordés dans la section précédente. Cependant, DWT est toujours implémenté comme une banque de filtres sous la forme d'une cascade de filtres passe-haut et passe-bas. Les banques de filtres sont un moyen très efficace de diviser un signal en plusieurs sous-bandes de fréquences.

Au premier stade avec une petite échelle, l'analyse du comportement à haute fréquence du signal. À la deuxième étape, l'échelle augmente d'un facteur deux (la fréquence diminue d'un facteur deux) et nous analysons le comportement de la moitié environ de la fréquence maximale. Au troisième stade, le facteur d'échelle est de quatre, et nous analysons le comportement en fréquence d'environ un quart de la fréquence maximale. Et cela continue jusqu'à ce que nous atteignions le niveau maximum de décomposition.

Le niveau maximal de décomposition peut être calculé à l'aide de la fonction pywt.wavedec (), tandis que la décomposition et les détails ressembleront à:

Annonce

 import pywt from pywt import wavedec from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data= sin (250 * pi * x**2) n_level=pywt.dwt_max_level(len(data), 'sym5') print('  : %s'%n_level) x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=7) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-7') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-7') grid() legend(loc='best') show()

Nous obtenons:

Niveau de décomposition maximum: 7

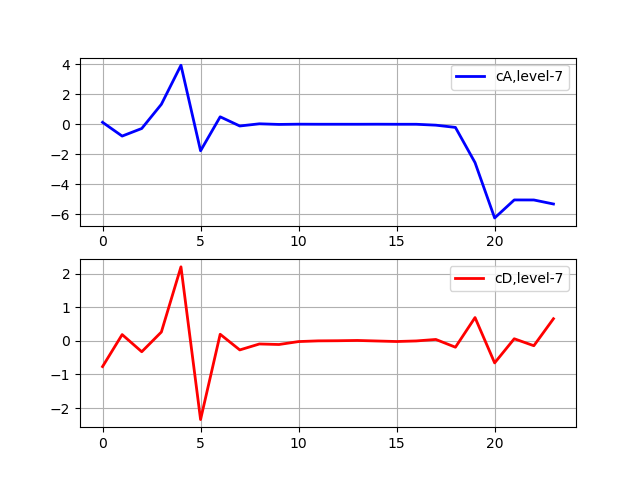
La décomposition s'arrête lorsque le signal devient plus court que la longueur du filtre pour une ondelette sym5 donnée. Par exemple, supposons que nous ayons un signal avec des fréquences allant jusqu'à 1000 Hz. À la première étape, nous séparons notre signal en parties basse et haute fréquence, c'est-à-dire 0-500 Hz et 500-1000 Hz. À la deuxième étape, nous prenons la partie basse fréquence et la divisons à nouveau en deux parties: 0-250 Hz et 250-500 Hz. Dans la troisième étape, nous avons divisé la partie 0-250 Hz en la partie 0-125 Hz et la partie 125-250 Hz. Cela continue jusqu'à ce que nous atteignions le niveau maximum de décomposition.

Analyse de fichiers wav à l'aide de scalogrammes de Fourier et d'ondelettes fft

Pour l'analyse, utilisez le fichier WebSDR . Considérons l'analyse du signal réduit à l'aide de triang de scipy.signal et la mise en œuvre de la transformée de Fourier discrète en python (fft de scipy.fftpack). Si la longueur de la séquence fft n'est pas égale à 2n, alors au lieu de la transformée de Fourier rapide (fft), une transformée de Fourier discrète (dft) sera effectuée. Voilà comment fonctionne cette équipe.

Nous utilisons le tampon de transformée de Fourier rapide selon le schéma suivant (données numériques par exemple):

fftbuffer = np.zeros (15); créer un tampon rempli de zéros;
fftbuffer [: 8] = x [7:]; déplacer la fin du signal vers la première partie du tampon; fftbuffer [8:] = x [: 7] - nous déplaçons le signal à partir de la dernière partie du tampon; X = fft (fftbuffer) - nous considérons la transformée de Fourier d'un tampon rempli de valeurs de signal.

Pour rendre le spectre de phase plus lisible, le déploiement de phase est applicable. Pour ce faire, modifiez la ligne avec le calcul de la caractéristique de phase: pX = np.unwrap (np.angle (X)).

Liste pour l'analyse des fragments de signal fft

 import numpy as np from pylab import * from scipy import * import scipy.io.wavfile as wavfile M=501 hM1=int(np.floor((1+M)/2)) hM2=int(np.floor(M/2)) (fs,x)=wavfile.read('WebSDR.wav') x1=x[5000:5000+M]*np.hamming(M) N=511 fftbuffer=np.zeros([N]) fftbuffer[:hM1]=x1[hM2:] fftbuffer[N-hM2:]=x1[:hM2] X=fft(fftbuffer) mX=abs(X) pX=np.angle(X) suptitle(" WebSDR") subplot(3, 1, 1) st='  (WebSDR.wav)' plot(x,linewidth=2, label=st) legend(loc='center') subplot(3, 1, 2) st='    ' plot(mX,linewidth=2, label=st) legend(loc='best') subplot(3, 1, 3) st='    ' pX=np.unwrap(np.angle(X)) plot(pX,linewidth=2, label=st) legend(loc='best') show()

Pour l'analyse comparative, nous utiliserons un scalogramme en ondelettes qui peut être construit en utilisant la fonction tree = pywt.wavedec (signal, 'coif5') dans matplotlib.

Liste des scalogrammes d'ondelettes

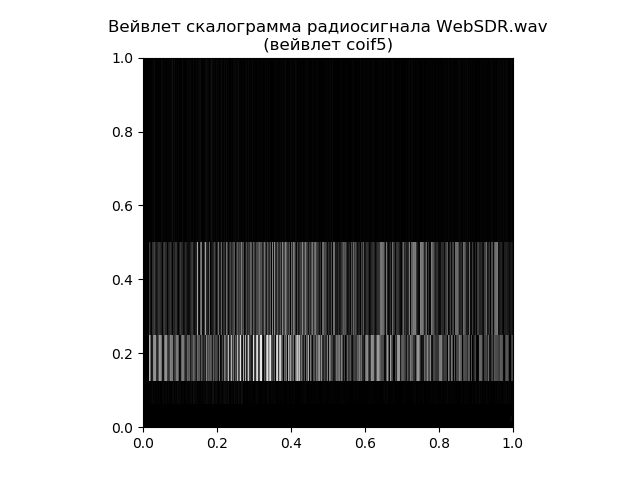
 from pylab import * import pywt import scipy.io.wavfile as wavfile #     ,     . def lepow2(x): return int(2 ** floor(log2(x))) #    MRA. def scalogram(data): bottom = 0 vmin = min(map(lambda x: min(abs(x)), data)) vmax = max(map(lambda x: max(abs(x)), data)) gca().set_autoscale_on(False) for row in range(0, len(data)): scale = 2.0 ** (row - len(data)) imshow( array([abs(data[row])]), interpolation = 'nearest', vmin = vmin, vmax = vmax, extent = [0, 1, bottom, bottom + scale]) bottom += scale #  ,   . rate, signal = wavfile.read('WebSDR.wav') signal = signal[0:lepow2(len(signal))] tree = pywt.wavedec(signal, 'coif5') gray() scalogram(tree) show()

Ainsi, le scalogramme donne une réponse plus détaillée à la question de la distribution des fréquences dans le temps, et la transformée de Fourier rapide est responsable des fréquences elles-mêmes. Tout dépend de la tâche, même pour un exemple aussi simple.

Conclusions

La justification de l'utilisation d'une transformée en ondelettes discrète pour les signaux dynamiques est donnée.
Des exemples d'analyse d'ondelettes utilisant PyWavelets 1.0.3, un logiciel open source gratuit publié sous la licence MIT, sont fournis.
Des outils logiciels pour une utilisation pratique de la bibliothèque PyWavelets sont considérés.

Analyse des ondelettes, partie 1

Présentation

Quand utiliser la transformée en ondelettes au lieu de la transformée de Fourier

Les principales propriétés des ondelettes

Modes d'extension du signal

Transformation en ondelettes discrète

Banque de filtres

Analyse de fichiers wav à l'aide de scalogrammes de Fourier et d'ondelettes fft

Conclusions

More articles: