En analysant un problème d'olympiade, nous irons le long des couloirs sinueux de la génération des labyrinthes et de leur passage, et nous verrons également que dans le langage Julia la simplicité de la mise en œuvre des algorithmes frise leur pseudo-code.

Défi

Le labyrinthe est un carré quadrillé de 10 sur 10, dans certaines cellules il y a des obstacles et dans une cellule il y a une sortie. Le robot est dans un tel labyrinthe et peut exécuter 4 commandes: déplacer une cellule vers le bas, le haut, la droite ou la gauche. Si le robot essaie d'aller au-delà des limites du labyrinthe ou d'entrer dans la cage avec un obstacle, il reste en place. Si le robot entre dans la sortie, il quitte le labyrinthe et ignore les autres commandes. Écrivez un programme pour le robot, exécutant ce que le robot arrive dans tous les cas à la sortie, quelle que soit la cellule dans laquelle il se trouvait au début. Le programme ne devrait pas comprendre plus de 1 000 équipes.

Format d'entrée

Il n'y a pas d'entrée. Vous devez écrire un programme pour une condition spécifique spécifiée
le labyrinthe.
La version du labyrinthe que vous pouvez copier. 0 - cellule libre, 1 - obstacle, x -
sortir.

0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000 

Format de sortie

Une ligne composée des caractères U, D, R, L d'une longueur ne dépassant pas 1000

La préparation

Ceux qui n'ont pas travaillé avec des graphiques dans Julia doivent télécharger des packages

 using Pkg Pkg.add("Plots") Pkg.add("Colors") Pkg.add("Images") Pkg.build("Images") #     

Il est plus pratique de travailler dans Jupyter, car les images seront affichées directement pendant le travail. Vous trouverez ici des informations sur l'installation, ainsi qu'une introduction et des tâches pour les débutants.

Dans l'état de notre tâche, il existe une version du labyrinthe pour copier

 S0 = "0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000" 

Pour dessiner un labyrinthe, vous devez créer une matrice. Comme nous ne voulons pas mettre les espaces manuellement, nous travaillerons avec la ligne:

 S1 = prod(s-> s*' ', '['*S0*']') # prod(fun, arr)    arr #     fun #  julia  *   "[ 0 0 1 1 0 1 0 0 1 1 \n 0 1 0 0 0 0 1 0 0 0 \n 0 1 1 0 x 0 0 0 0 0 \n 0 0 1 0 0 0 0 1 0 0 \n 0 0 0 0 1 1 1 0 0 0 \n 0 0 0 0 1 0 0 1 0 0 \n 0 0 0 0 0 1 0 0 1 0 \n 0 1 0 0 1 0 1 0 1 0 \n 0 0 1 1 0 0 1 0 1 0 \n 1 0 0 0 0 1 1 0 0 0 ] " 

En remplaçant la lettre maladroite x par un nombre et en analysant la chaîne, nous obtenons une matrice entière définissant notre labyrinthe. Ensuite, pour plus de commodité, changez les uns en zéros et les zéros en uns et entourez le labyrinthe d'un mur:

 S2 = replace(S1, 'x'=>'9') M0 = S2 |> Meta.parse |> eval m,n = size(M0) M1 = replace(M0, 1=>0, 0=>1) M = zeros(Int64,m+2,n+2) for i in 2:m+1, j in 2:n+1 M[i,j] = M1[i-1,j-1] end M # Maze map matrix 12×12 Array{Int64,2}: 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 

Dans la matrice

 length(M) 144 

les cellules et d'eux

 sum(M)-9 70 

sur lequel vous pouvez marcher, c'est-à-dire des positions de départ potentielles. Vous pouvez afficher le résultat en construisant un histogramme bidimensionnel

 using Plots heatmap(M, yaxis = :flip) # flip -   

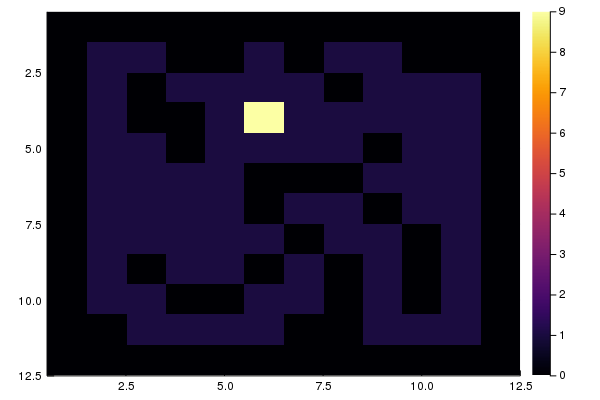
Vérification de la solution

Tout d'abord, vous devez élaborer des procédures qui vérifieront l'exactitude de la solution proposée. Définissez le type composite Point pour utiliser la terminologie des points et des coordonnées:

 mutable struct Point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end 

Et maintenant, vous devez apprendre à traduire une séquence de commandes compréhensibles par le robot en code.

L'idée est assez simple: il y a une coordonnée de départ, une ligne propose un algorithme indiquant comment marcher. Nous prenons une lettre et regardons laquelle des cellules voisines marcher. À la coordonnée actuelle, nous ajoutons la valeur qui est stockée dans cette cellule. Autrement dit, s'il y a zéro (mur), nous n'avons bougé nulle part, sinon nous avons fait un petit pas dans la direction requise.

En utilisant la puissance de la métaprogrammation, vous pouvez remplacer la séquence entrante de directions par un code volumineux et uniforme et l'exécuter

 S = "RRLDUURULDDRDDRRRUUU" S1 = replace(S , "R"=>"c.y+=M[cx, c.y+1];") S1 = replace(S1, "L"=>"cy-=M[cx, cy-1];") S1 = replace(S1, "U"=>"c.x+=M[c.x+1, cy];") S1 = replace(S1, "D"=>"cx-=M[cx-1, cy];") #  - start point Sp = eval( Meta.parse(S1) ) 

Mais cette méthode présente un certain nombre d'inconvénients, par conséquent, nous utiliserons les opérateurs conditionnels classiques. Soit dit en passant, le fait que la sortie soit indiquée par le nombre 9 est une petite astuce: afin de ne pas vérifier chaque cellule, et si c'est la sortie, nous initions le mouvement en ajoutant la valeur stockée dans une cellule spécifique. Lorsque le robot monte sur la sortie, un nombre délibérément élevé est ajouté à ses coordonnées, de sorte que le robot vole au-delà des limites du tableau, ce qui peut être détecté comme une erreur en utilisant le bloc:

 try #     catch #       end 

Ainsi, nous implémentons une fonction qui vérifiera si le robot atteint la sortie à partir du point c exécutant des commandes à partir de la chaîne str :

 function isexit(str, c) scatter!([cy],[cx]) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end 

Collectons une fonction qui itérera sur toutes les positions de départ

 function test(Str) k = 0 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end 

Vérifiez les commandes:

 S = "RRRLDUUURRRUUURRRRLLLRRUULDDDDRRRRDDDRRRUUU" heatmap(M, yaxis = :flip) test(S) # 10 test completed from 70 plot!(legend = false) 

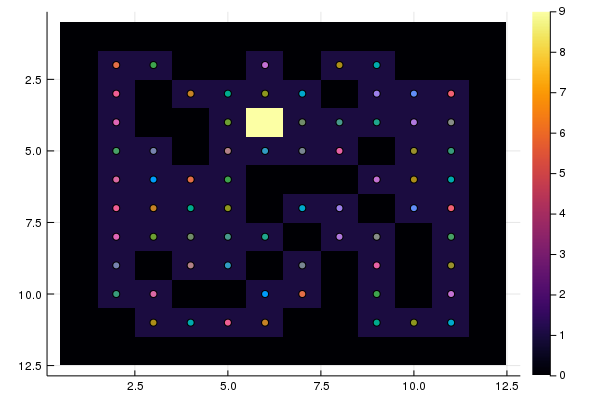
Tous les points de départ ont été testés et seulement 10 ont conduit à la sortie. Il est nécessaire de construire des itinéraires de chaque point jusqu'à la sortie.

Avant de plonger dans la génération et le passage des labyrinthes, nous enregistrerons nos résultats. Nous utiliserons le package Images.jl qui offre de nombreuses possibilités dans le domaine du traitement d'image (un bon exemple ). L'un de ses outils de support est le package Colors.jl , qui étend la capacité de Julia à travailler avec les couleurs.

 using Images clrs(x) = x==9 ? RGB(1.,0.5,0) : RGB(x,x,x) maze = clrs.(M) # maze = Gray.(maze) # save("D:/dat/maze12x12.png", maze) 

Recherche de profondeur

Mise en œuvre de l'idée à partir d'un article sur le Habr .
L'idée est simple: créer une grille de murs

 M = 10 N = 10 A = [ i&j&1 for i in 0:N, j in 0:M ] # isodd(i) & isodd(j) & 1 Gray.(A) # from Images.jl 

puis, en boucle, nous traversons la route et les branches. Nous définissons une fonction qui trouve les zones non visitées voisines (nous les désignerons, disons, par un diable) et renvoie l'un de ces voisins (s'il n'y a pas de voisins non visités, il renvoie un point de drapeau):

 function neighbours2(A,p, n, m) nbrs = [Point(px, p.y+2), # up Point(px, py-2), # down Point(px-2, py), # left Point(p.x+2, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==2 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(-1,-1) end 

Nous allons briser les murs comme ceci:

 function breakwall(A, newp,oldp) #  : x = (newp.x + oldp.x) >> 1 #   y = (newp.y + oldp.y) >> 1 A[x,y] = 1 end 

Algorithme

1. Activez la cellule initiale et marquez-la comme visitée.
2. Bien qu'il y ait des cellules non visitées
   1. Si la cellule actuelle a des «voisins» non visités
   1. Poussez la cellule actuelle sur la pile
   2. Sélectionnez une cellule aléatoire de voisin
   3. Supprimez le mur entre la cellule actuelle et la cellule sélectionnée
   4. Activez la cellule sélectionnée et marquez-la comme visitée.
   2. Sinon, si la pile n'est pas vide
   1. Retirez la cage de la pile
   2. Rendez-le à jour
   3. Sinon
   1. Sélectionnez une cellule aléatoire non visitée, actualisez-la et marquez-la comme visitée.

 function amazeng(n, m) M = [ 2(i&j&1) for i in 0:n, j in 0:m ]; p = Point(2,2) #   lifo = [] #   push!(lifo, p) #i = 0 while length(lifo) != 0 #     M[px,py] = 1 #     np = neighbours2(M, p, n, m) # new point #    -   if np.x == np.y == -1 p = pop!(lifo) else push!(lifo, p) breakwall(M, np, p) p = np #i+=1 #maze = Gray.(M/2) #save("D:/dat/maze$i.png", maze) end end M[1,2] = 1 #  M[n,m+1] = 1 #  Gray.(M) end 

 lbrnt = amazeng(36, 48) # save("D:/dat/maze111.png", lbrnt) 

Algorithme de recherche de chemin de retour en arrière:

1. Activez la cellule initiale et marquez-la comme visitée.
2. Jusqu'à ce qu'une solution soit trouvée
   1. Si la cellule actuelle a des «voisins» non visités
   1. Poussez la cellule actuelle sur la pile
   2. Sélectionnez une cellule aléatoire de voisin
   3. Activez la cellule sélectionnée et marquez-la comme visitée.
   2. Sinon, si la pile n'est pas vide
   1. Retirez la cage de la pile
   2. Rendez-le à jour
   3. Sinon, il n'y a pas d'issue.

Nous recherchons des voisins au contraire et dans le rayon d'une cellule, et non à travers une:

 function neighbours1(A, p, n, m) nbrs = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==1 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(0,0) end 

Définissez un algorithme pour passer le labyrinthe en dessinant l'itinéraire et les tentatives infructueuses

 function amazeng(img, start, exit) M = Float64.(channelview(img)) n, m = size(M) p = start M[exit.x,exit.y] = 1 lifo = [] push!(lifo, p) while px != exit.x || py != exit.y M[px,py] = 0.4 np = neighbours1(M, p, n, m) if np.x == np.y == 0 M[px,py] = 0.75 p = pop!(lifo) #  -  ,    #      else push!(lifo, p) p = np end end Gray.(M) end 

Comme certains l'ont remarqué, une fonction est également appelée, comme celle que les algorithmes génèrent (ordonnancement multiple). Lorsque vous l'appelez avec deux nombres, cela fonctionnera sur la méthode de construction du labyrinthe, mais si vous l'appelez en spécifiant l'image et deux points (les coordonnées de l'entrée et de la sortie) comme argument, puis à la sortie, nous obtenons une image avec le labyrinthe passé

 img0 = load("D:/dat/maze111.png") amazeng(img0) 

Essayons notre labyrinthe:

 img0 = load("D:/dat/maze12x12.png") n, m = size(img0) amazeng(img0, Point(11,9), Point(4,6) ) 

Même si vous modifiez la fonction pour que la route soit mémorisée, l'algorithme s'avère toujours inefficace à cause des espaces ouverts. Mais les labyrinthes sortent très bien.

Algorithme randomisé de Prim

Dès que vous commencez à dessiner des labyrinthes, vous ne vous arrêterez pas. Réalisons un autre algorithme intéressant:

• Commencez avec une grille pleine de murs.
• Sélectionnez une cellule, marquez-la comme faisant partie du labyrinthe. Ajoutez des murs de cellules à la liste des murs.
• Bien qu'il y ait des murs dans la liste:
  
  • Sélectionnez un mur au hasard dans la liste. Si une seule des deux cellules partagées par le mur est visitée, alors:
    
    • Faites du mur un passage et marquez la cellule non visitée comme faisant partie du labyrinthe.
    • Ajoutez des murs de cellules adjacents à la liste des murs.
  • Retirez le mur de la liste.

 neighbors(p::Point) = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right function newalls!(walls, p, maze, n, m) nbrs = neighbors(p) for a in nbrs if 1<ax<n-1 && 1<ay<m-1 && !maze[ax,ay] push!(walls, a) #       . end end end function breakwall!(p, maze, n, m) nbrs = neighbors(p) #       if sum( a-> maze[ax,ay], nbrs) == 1 for a in nbrs if maze[ax,ay] # true =  px == ax ? nx = px : px>ax ? nx = p.x+1 : nx = px-1 py == ay ? ny = py : py>ay ? ny = p.y+1 : ny = py-1 maze[px,py] = true #   maze[nx,ny] = true px = nx py = ny return true end end else return false end end function prim(n, m) M = falses(n,m); #    p = Point(2, 2) M[px,py] = true walls = [] newalls!(walls, p, M, n, m) while length(walls) != 0 p = splice!( walls, rand(1:length(walls)) ) if breakwall!(p, M, n, m) newalls!(walls, p, M, n, m) end end M end 

 primaze = prim(19,19); Gray.(primaze) 

Il s'avère plus ramifié et non moins génial, en particulier le processus d'assemblage.

Et maintenant, nous implémentons l'algorithme le plus courant pour trouver l'itinéraire le plus court:

Méthode A *

• 2 listes de sommets sont créées - en attente et déjà examinées. Un point de départ est ajouté à ceux en attente, la liste des révisés jusqu'à présent est vide.
• Pour chaque point est calculé $$$H$ - la distance approximative du point à la cible.
• Dans la liste des points à considérer, le point avec le plus petit $$$H$ . Laisse-la $$$X$ .
• Si $$$X$ - le but, puis nous avons trouvé l'itinéraire.
• Nous portons $$$X$ de la liste en attente à la liste des déjà examinés.
• Pour chacun des points adjacents à $$$X$ (dénotez ce point voisin $$$Y$ ), procédez comme suit:
  
  • Si $$$Y$ déjà dans la revue - sautez-la.
  • Si $$$Y$ pas encore sur la liste d'attente - ajoutez-le ici.
• Si la liste des points à considérer est vide, mais que nous n'avons pas atteint l'objectif, alors l'itinéraire n'existe pas.

Pour commencer, définissons la classe "point" qui saura à quelle distance elle est de la cible:

 mutable struct Point_h x::Int64 # horisont y::Int64 # vertical h::Float64 Point_h(x, y) = new(x, y, 0.) end 

Nous définissons maintenant une opération de comparaison pour la structure, une méthode pour établir la présence d'un élément dans un tableau, ainsi que la fonction de suppression d'un élément, de recherche de la distance entre les points et de listage des voisins:

 import Base: in, == ==(a::Point_h, b::Point_h) = ax==bx && ay==by function in(p::Point_h, Arr::Array{Point_h,1}) for a in Arr if a == p return true end end return false end function splicemin!(Arr)#::Array{Point_h,1} i = argmin( [ah for a in Arr] ) splice!(Arr, i) end dista(u,v) = hypot(vx-ux, vy-uy) # <=> sqrt( (vx-ux)^2 + (vy-uy)^2 ) neighbors(p::Point_h) = [Point_h(px, p.y+1), # up Point_h(px, py-1), # down Point_h(px-1, py), # left Point_h(p.x+1, py)] # right 

Comme toujours, les opérateurs obscurs peuvent être clarifiés en utilisant la commande ? par exemple ?splice ?argmin .

Et, en fait, la méthode A * elle-même

 function astar(M, start, final) #   -       isgood(p) = 1<px<n && 1<py<m && M[px,py] != 0 n, m = size(M) #       start.h = dista(start,final) closed = [] opened = [] push!(opened, start) while length(opened) != 0 X = splicemin!(opened) if X in closed continue end if X == final break end push!(closed, X) nbrs = neighbors(X) ygrex = filter(isgood, nbrs) for Y in ygrex if Y in closed continue else Yh = dista(Y, final) push!(opened, Y) end end end #    closed # return end 

Nous chargeons l'image avec le labyrinthe et la présentons sous la forme d'une matrice:

 img0 = load("D:/dat/maze0.png") mazematrix = Float64.(channelview(img0)) 

Et nous construisons une route pour sortir d'un point arbitraire:

 s = Point_h(11,9) # start f = Point_h(4,6) # finish M = copy(mazematrix) route = astar(M, s, f) i = 1 for c in route #   M[cx,cy] = 0.7 #save("D:/dat/Astar$i.png", M) i+=1 end Gray.(M) 

Une recherche de toutes les positions ressemble à ceci:

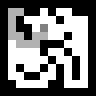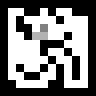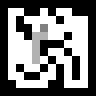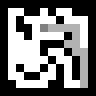
Vu que l'agent se précipiter tend toujours du côté de la sortie et se transforme souvent en impasses, ce qui donne lieu à des étapes inutiles, et tout le parcours est mémorisé. Ceci est évité par une version légèrement plus complexe de l'algorithme A *.

• 2 listes de sommets sont créées - en attente et déjà examinées. Un point de départ est ajouté à ceux en attente, la liste des révisés jusqu'à présent est vide.
• Pour chaque point est calculé $$$F = G + H$ . $$$G$ - distance du début au point, $$$H$ - la distance approximative du point à la cible. Chaque point stocke également un lien vers le point d'où il provient.
• Dans la liste des points à considérer, le point avec le plus petit $$$F$ . Laisse-la $$$X$ .
• Si $$$X$ - le but, puis nous avons trouvé l'itinéraire.
• Nous portons $$$X$ de la liste en attente à la liste des déjà examinés.
• Pour chacun des points adjacents à $$$X$ (dénotez ce point voisin $$$Y$ ), procédez comme suit:
  
  • Si $$$Y$ déjà dans la revue - sautez-la.
  • Si $$$Y$ pas encore sur la liste d'attente - ajoutez-le ici, en vous souvenant du lien vers $$$X$ et ayant calculé $$$Y.G$ (c'est $$$X.G$ + distance de $$$X$ avant $$$Y$ ) et $$$Y.H$ .
  • Si $$$Y$ dans la liste pour examen - vérifier si $$$X.G$ + distance de $$$X$ avant $$$Y$$$$<Y.G$ nous sommes donc arrivés au point $$$Y$ manière plus courte, remplacer $$$Y.G$ sur $$$X.G$ + distance de $$$X$ avant $$$Y$ , et le point d'où ils sont venus $$$Y$ sur $$$X$ .
• Si la liste des points à considérer est vide, mais que nous n'avons pas atteint l'objectif, alors l'itinéraire n'existe pas.

Mais même avec des étapes inutiles, notre option est bien dans la limite de la tâche, donc la modification des programmes sera votre devoir.

Jusqu'à la fin de l'Olympiade, il ne restait plus rien, mais nous devons encore apprendre à traduire les résultats de nos algorithmes en commandes de la forme "RRLUUDL..."

Et après toutes ces promenades dans les dédales, on peut supposer que la solution est beaucoup plus simple. En fait, une option simple demande tout de suite, mais je voulais vraiment faire de belles choses .

Si nous plaçons notre artiste dans un espace ouvert et initions des promenades aléatoires, il hésitera près de sa position de départ. Mais avec l'introduction des murs, certaines directions commenceront à s'estomper, les degrés de liberté deviendront moindres et avec les mêmes données d'entrée, l'agent se déplacera sur une plus grande distance.

Voici notre version de vérification de la pertinence des équipes pour sauver un robot d'un labyrinthe:

 M = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0] mutable struct Point # point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end function isexit(str, c) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end function test(Str) k = 0 n, m = 10,10 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end 

Il suffit maintenant de générer des lignes aléatoires jusqu'à ce que vous en obteniez une qui fonctionne pour toutes les positions de départ:

 using Random S = randstring("RLUD",200) "RDRRRDLRLUULURUDUUDLLLLLULLUDRRURDLDLULLRLUUUDURUUUULRUDUURUUDLRLLULRLUDRRLRRULLDULRRRRULRLLDULRLDRUDURDRUUDUUDDDDDLURRRRDRDURRRDDLLDUURRRLDRUDLRLLRDDRLRRRDDLLLRUURDRLURDLLUULLLLUURLLULUDULDDLDLLRLDUD" test(S) 41 test completed from 70 

De plus, il était possible de ne pas se soucier du test. Il suffisait de lire la tâche et de générer une chaîne aléatoire avec la condition maximale autorisée:

 for i in 1:20 S = randstring("RLUD",1000) test(S) end 70 test completed from 70 70 test completed from 70 70 test completed from 70 70 test completed from 70 55 test completed from 70# 65 test completed from 70# 70 test completed from 70 70 test completed from 70 38 test completed from 70# 70 test completed from 70 70 test completed from 70 56 test completed from 70# 70 test completed from 70 70 test completed from 70 70 test completed from 70 16 test completed from 70# 70 test completed from 70 24 test completed from 70# 70 test completed from 70 70 test completed from 70 

Autrement dit, avec une probabilité de 70%, la ligne passerait les tests.

C’est tout. Je souhaite au lecteur un hasard, une patience et une intuition réussis pour des solutions évidentes.

Pour les curieux - liens pour approfondir le sujet:

• L'excursion la plus complète dans la génération du labyrinthe
• Version russe
• Méthodes de temps
• Deux méthodes
• Algorithme Eller
• Générateur en ligne
• Méthodes pour trouver le chemin entre les points en ligne
• Algorithme de chemin de recherche de point de saut
• A * sur Wikipédia
• Introduction à A *
• Introduction à l'algorithme A *
• Explication des algorithmes de recherche de chemin
• Source d'art