Ce commentaire a été suscité par la rédaction de l'article. Plus précisément, une phrase de celui-ci.

... dépenser des cycles de mémoire ou de processeur sur des articles en milliards de dollars n'est pas bon ...

Il se trouve que récemment, je devais faire exactement cela. Et, bien que le cas que j'examinerai dans l'article soit assez spécial - les conclusions et les solutions appliquées peuvent être utiles à quelqu'un.

Un peu de contexte

L'application iFunny traite une énorme quantité de contenu graphique et vidéo, et la recherche floue de doublons est l'une des tâches très importantes. C'est en soi un gros sujet qui mérite un article séparé, mais aujourd'hui je vais juste parler un peu de certaines approches pour calculer de très grands tableaux de nombres par rapport à cette recherche. Bien sûr, tout le monde a une compréhension différente des «très grands réseaux», et il serait stupide de rivaliser avec le Hadron Collider, mais quand même. :)

Si l'algorithme est très court, alors pour chaque image sa signature numérique (signature) est créée à partir de 968 entiers, et la comparaison est faite en trouvant la "distance" entre les deux signatures. Étant donné que le volume de contenu au cours des deux derniers mois à lui seul s'est élevé à environ 10 millions d'images, un lecteur attentif pourra facilement le comprendre dans son esprit - ce sont exactement les «éléments en milliards de volumes». Peu importe - bienvenue au chat.

Au début, il y aura une histoire ennuyeuse sur le gain de temps et de mémoire, et à la fin il y aura une courte histoire instructive sur le fait qu'il est parfois très utile de regarder la source. Une image pour attirer l'attention est directement liée à cette histoire instructive.

Je dois admettre que j'étais un peu rusé. Dans une analyse préliminaire de l'algorithme, il a été possible de réduire le nombre de valeurs dans chaque signature de 968 à 420. C'est déjà deux fois plus bon, mais l'ordre de grandeur reste le même.

Bien que, si vous y réfléchissez, je ne suis pas si trompeur, et ce sera la première conclusion: avant de commencer la tâche, il convient de réfléchir - est-il possible de la simplifier d'une manière ou d'une autre à l'avance?

L'algorithme de comparaison est assez simple: la racine de la somme des carrés des différences des deux signatures est calculée, divisée par la somme des valeurs précédemment calculées (c'est-à-dire qu'à chaque itération, la somme sera toujours et ne pourra pas être considérée comme une constante) et comparée à la valeur de seuil. Il convient de noter que les éléments de signature sont limités aux valeurs de -2 à +2 et, par conséquent, la valeur absolue de la différence est limitée aux valeurs de 0 à 4.


Rien de compliqué, mais la quantité décide.

Première approche, naïve

//  const val d = 0.3 // 10.000.000 . //      , //        val collection: MutableList<Signature> = mutableListOf() // signature —   420   Byte class Signature(val signature: Array<Byte>, val norma: Double) fun getSimilar(signature: Signature) = collection .filter { calculateDistance(it, signature) < d } fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> Math.pow((value - second.signature[index]).toDouble(), 2.0) }.sum()) / (first.norma + second.norma) 

Calculons ce que nous avons ici avec le nombre d'opérations:

10M Square Roots Math.sqrt
10M et divisions de 10M / (first.norma + second.norma)
4.200M soustractions et quadrature Math.pow((value - second.signature[index]).toDouble(), 2.0)
4.200M ajouts .sum()

Quelles options avons-nous:

1. Avec de tels volumes, dépenser un Byte entier (ou, Dieu ne plaise, quelqu'un aurait deviné utiliser Int ) pour stocker trois bits importants est un gaspillage impardonnable.
2. Peut-être, comment réduire la quantité de mathématiques?
3. Mais est-il possible de faire un filtrage préliminaire, qui n'est pas si coûteux en calcul?

La deuxième approche, nous emballons

Soit dit en passant, si quelqu'un suggère comment vous pouvez simplifier les calculs avec un tel emballage, vous recevrez un grand merci et plus en karma. Bien qu'un, mais de tout mon cœur :)

Un Long est de 64 bits, ce qui, dans notre cas, nous permettra d'y stocker 21 valeurs (et 1 bit restera non réglé).

 //   20   Long class Signature(val signature: Array<Long>, val norma: Double) fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> calculatePartial(value, second.signature[index]) }.sum()) / (first.norma + second.norma) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L (0..60 step 3).onEach { val current = (first.ushr(it) and 0x7) - (second.ushr(it) and 0x7) sum += current * current } return sum.toDouble() } 

C'est mieux de la mémoire ( 4.200M contre 1.600M octets, si grosso modo), mais qu'en est-il des calculs?

Je pense qu'il est évident que le nombre d'opérations est resté le même et que 8.400M décalages et 8.400M logiques y ont 8.400M ajoutés. Peut-être que cela peut être optimisé, mais la tendance n'est toujours pas heureuse - ce n'est pas ce que nous voulions.

La troisième approche, reconditionner avec des sous-sous-marins

Le matin, je me sens, ici, vous pouvez utiliser un peu de magie!

Stockons les valeurs non pas en trois, mais en quatre bits. De cette façon:

Oui, nous perdrons la densité d'emballage par rapport à la version précédente, mais nous aurons la possibilité de recevoir Long avec 16 différences (pas tout à fait) avec un XOR 'ohm à la fois. De plus, il n'y aura que 11 options pour la distribution des bits dans chaque quartet final, ce qui vous permettra d'utiliser des valeurs précalculées des carrés des différences.

 //   27   Long class Signature(val signature: Array<Long>, val norma: Double) // -1    val precomputed = arrayOf(0, 1, 1, 4, 1, -1, 4, 9, 1, -1, -1, -1, 4, -1, 9, 16) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L val difference = first xor second (0..60 step 4).onEach { sum += precomputed[(difference.ushr(it) and 0xF).toInt()] } return sum.toDouble() } 

De mémoire, il est devenu 2.160M contre 1.600M - désagréable, mais toujours meilleur que le 4.200M initial.

Calculons les opérations:

10M racines carrées, ajouts et divisions (pas allé nulle part)
270M XOR
4.320 ajouts, décalages, 4.320 logiques et extraits de la matrice.

Cela semble déjà plus intéressant, mais de toute façon, il y a trop de calculs. Malheureusement, il semble que nous ayons déjà dépensé ces 20% des efforts pour donner 80% du résultat et il est temps de réfléchir à d'autres sources de profit. La première chose qui me vient à l'esprit est de ne pas le faire du tout, en filtrant les signatures manifestement inappropriées avec un filtre léger.

Quatrième approche, grand tamis

Si vous transformez légèrement la formule de calcul, vous pouvez obtenir cette inégalité (plus la distance calculée est petite, mieux c'est):


C'est-à-dire maintenant, nous devons comprendre comment calculer la valeur minimale possible du côté gauche de l'inégalité sur la base des informations que nous avons sur le nombre de bits définis dans Long . Ensuite, jetez simplement toutes les signatures qui ne le satisfont pas.
Permettez-moi de vous rappeler que x _i peut prendre des valeurs de 0 à 4 (le signe n'est pas important, je pense que c'est clair pourquoi). Étant donné que chaque terme est au carré, il est facile de dériver un modèle général:


La formule finale ressemble à ceci (nous n'en avons pas besoin, mais je l'ai déduit pendant longtemps et il serait dommage d'oublier et de ne montrer à personne):


Où B est le nombre de bits défini.

En fait, dans un seul Long de 64 bits, lisez 64 résultats possibles. Et ils sont parfaitement calculés à l'avance et ajoutés à un tableau, par analogie avec la section précédente.

De plus, il est complètement facultatif de calculer les 27 Longs - il suffit de dépasser le seuil au prochain et vous pouvez interrompre le contrôle et retourner faux. Soit dit en passant, la même approche peut être utilisée dans le calcul principal.

 fun getSimilar(signature: Signature) = collection .asSequence() //     !? .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } val estimateValues = arrayOf(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 69, 74, 79, 84, 89, 94, 99, 104, 109, 114, 119, 124, 129, 134, 139, 144, 151, 158, 165, 172, 179, 186, 193, 200, 207, 214, 221, 228, 235, 242, 249, 256) fun estimate(first: Signature, second: Signature):Boolean{ var bitThreshold = Math.pow(d * (first.norma + second.norma), 2.0).toLong() first.signature.forEachIndexed { index, value -> bitThreshold -= estimateValues[java.lang.Long.bitCount(value xor second.signature[index])] if (bitThreshold <= 0) return false } return true } 

Ici, il faut comprendre que l'efficacité de ce filtre (jusqu'à négatif) dépend de façon désastreuse du seuil sélectionné et, un peu moins fortement, des données d'entrée. Heureusement, pour le seuil requis d=0.3 un nombre assez faible d'objets réussit à passer le filtre et la contribution de leur calcul au temps de réponse total est si faible qu'ils peuvent être négligés. Et si c'est le cas, vous pouvez économiser un peu plus.

Cinquième approche, se débarrasser de la séquence

Lorsque vous travaillez avec de grandes collections, la sequence est une bonne défense contre la mémoire extrêmement désagréable. Cependant, si nous savons évidemment que sur le premier filtre, la collection sera réduite à une taille saine, un choix beaucoup plus raisonnable serait d'utiliser l'itération ordinaire en boucle avec la création d'une collection intermédiaire, car la sequence n'est pas seulement à la mode et jeune, mais aussi un itérateur, qui a des compagnons suivants qui sont loin d'être gratuits.

 fun getSimilar(signature: Signature) = collection .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } 

Il semblerait qu'ici c'est le bonheur, mais je voulais "le rendre beau". Nous arrivons ici à l'histoire instructive promise.

Sixième approche, nous voulions le meilleur

Nous écrivons sur Kotlin, et voici quelques java.lang.Long.bitCount étrangers! Et plus récemment, des types non signés ont été introduits dans la langue. Attaque!

Aussitôt dit, aussitôt fait. Tous les ULong remplacés par ULong , ULong extrait de la source Java et réécrit en tant que fonction d'extension pour ULong

 fun ULong.bitCount(): Int { var i = this i = i - (i.shr(1) and 0x5555555555555555uL) i = (i and 0x3333333333333333uL) + (i.shr(2) and 0x3333333333333333uL) i = i + i.shr(4) and 0x0f0f0f0f0f0f0f0fuL i = i + i.shr(8) i = i + i.shr(16) i = i + i.shr(32) return i.toInt() and 0x7f } 

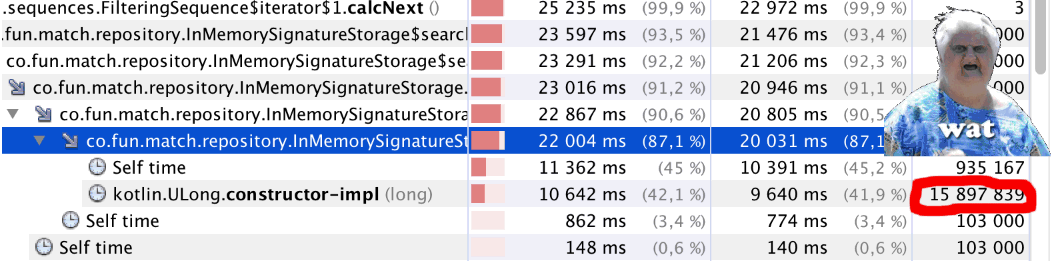
Nous commençons et ... Quelque chose ne va pas. Le code a commencé à fonctionner sensiblement plus lentement. Nous démarrons le profileur et voyons quelque chose d'étrange (voir le bitCount() article): un peu moins d'un million d'appels à bitCount() près de 16 millions d'appels à Kotlin.ULong.constructor-impl . WAT!?

L'énigme est expliquée simplement - il suffit de regarder le code de classe ULong

 public inline class ULong @PublishedApi internal constructor(@PublishedApi internal val data: Long) : Comparable<ULong> { @kotlin.internal.InlineOnly public inline operator fun plus(other: ULong): ULong = ULong(this.data.plus(other.data)) @kotlin.internal.InlineOnly public inline operator fun minus(other: ULong): ULong = ULong(this.data.minus(other.data)) @kotlin.internal.InlineOnly public inline infix fun shl(bitCount: Int): ULong = ULong(data shl bitCount) @kotlin.internal.InlineOnly public inline operator fun inc(): ULong = ULong(data.inc())  .. } 

Non, je comprends tout, ULong est experimental maintenant, mais comment ça!?
En général, nous reconnaissons que l'approche a échoué, ce qui est dommage.

Eh bien, mais peut-être que quelque chose d'autre peut être amélioré?

En fait, vous le pouvez. Le code java.lang.Long.bitCount origine n'est pas le plus optimal. Cela donne un bon résultat dans le cas général, mais si nous savons à l'avance sur quels processeurs notre application fonctionnera, alors nous pouvons choisir une manière plus optimale - voici un très bon article à ce sujet sur Habré.Je recommande vivement de compter les bits simples .

J'ai utilisé la "méthode combinée"

 fun Long.bitCount(): Int { var n = this n -= (n.shr(1)) and 0x5555555555555555L n = ((n.shr(2)) and 0x3333333333333333L) + (n and 0x3333333333333333L) n = ((((n.shr(4)) + n) and 0x0F0F0F0F0F0F0F0FL) * 0x0101010101010101).shr(56) return n.toInt() and 0x7F } 

Compter les perroquets

Toutes les mesures ont été effectuées au hasard, lors du développement sur la machine locale et sont reproduites de mémoire, il est donc difficile de parler de précision, mais vous pouvez estimer la contribution approximative de chaque approche.

Conclusions

• Lorsqu'il s'agit de traiter de grandes quantités de données, il vaut la peine de consacrer du temps à une analyse préliminaire. Peut-être que toutes ces données n'ont pas besoin d'être traitées.
• Si vous pouvez utiliser un pré-filtrage grossier mais bon marché, cela peut être très utile.
• La magie un peu est notre tout. Eh bien, le cas échéant, bien sûr.
• Regarder les codes sources des classes et fonctions standard est parfois très utile.

Merci de votre attention! :)

Et oui, à suivre.