Pour transmettre un message d'une station de base à un appareil mobile (et vice versa), une onde électromagnétique doit surmonter un nombre considérable d'obstacles: réflexion, réfraction, diffusion, ombrage, décalages de fréquence Doppler, etc. Tout d'abord, tous ces effets sont appelés multiplicatifs (de l'anglais. Multiplication - multiplication) - selon le modèle mathématique de ces effets. Et, d'autre part, il peut être collecté sous le terme général de décoloration .

De standard en standard, de génération en génération, de technologie en technologie, les scientifiques et les ingénieurs se sont débattus et ont du mal à niveler ces évanouissements (atténuation des évanouissements).

Et certaines solutions sont répandues. Disons plus: presque tous, d'une manière ou d'une autre, sont associés au concept de diversité .

La source de l'illustration (non, ce n'est pas de la publicité, juste une combinaison réussie du terme souhaité et du chat).

Un exemple de telles solutions:

Saut de fréquence - contre les évanouissements sélectifs en fréquence;
Estimation et égalisation des canaux par rétroaction - GSM, pour supprimer les changements dans le domaine temporel;
Extension du spectre (UMTS);
Signaux pilotes (commençant par UMTS) sur la liaison descendante (liaison descendante) et suivi du signal (suivi du signal) sur la liaison montante (liaison montante) - pour supprimer les changements dans le domaine temporel;
OFDM - LTE, contre les évanouissements sélectifs en fréquence;
Diversité temporelle ( codage correcteur d'erreurs );
Diversité de polarisation (côté émetteur) + Additionneurs (combineurs, côté récepteur);
Diversité spatiale .

La dernière de ces techniques que nous considérerons aujourd'hui dans le cadre d'un autre sujet sur MIMO .

Ordre de diversité d'espace et gain de réseau

Le premier.

Il existe un tel concept - l'ordre de la diversité de l'espace: si les mêmes informations peuvent être collectées dans différentes directions , alors l'espoir de les restaurer augmentera correctement. À titre d'exemple tiré de la vie, nous pouvons imaginer recueillir des informations sur le même événement à partir de sources informatives indépendantes. Dans les communications radio, nous pouvons augmenter cette commande, notamment en utilisant MISO , SIMO ou MIMO .

La limite théorique d'une telle diversité M_TM_R où M_T - le nombre d'antennes d'émission, et M_R - le nombre d'antennes de réception. N'oubliez pas cela.

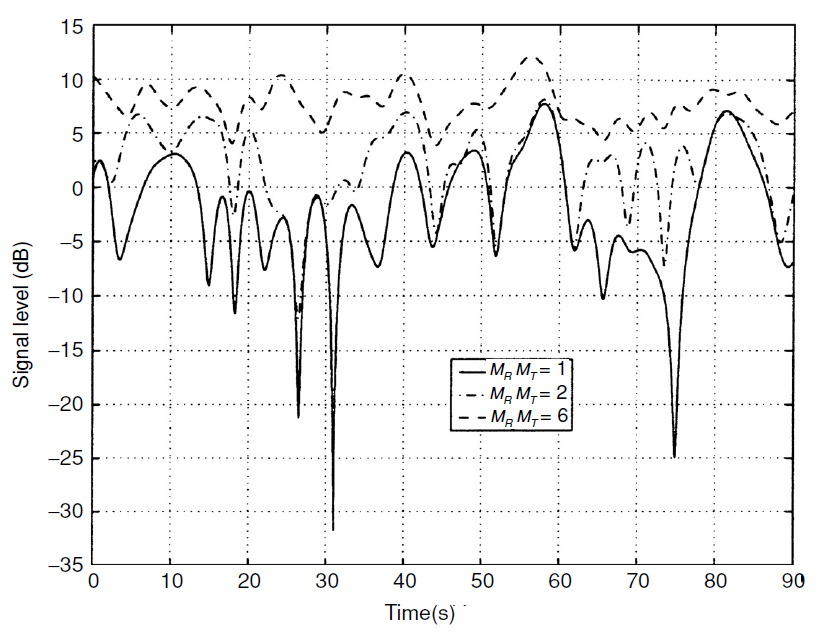
Fig.1. Stabilité des canaux causée par une augmentation de l'ordre de diversité spatiale. Aux valeurs $M_TM_R \ to \ infty$ le canal est entièrement stabilisé et se transformera en canal sans décoloration (AWGN) [1, p . 101] .

Le deuxième.

En utilisant SIMO , MIMO et même MISO (dans le cas d'un canal bien connu), on peut obtenir ce que l'on appelle le gain de réseau . Cela signifie que l'utilisation de plusieurs antennes de réception et / ou la répartition correcte de l'énergie du côté émission peut augmenter le rapport signal / bruit (SNR) - et ainsi réduire le nombre d'erreurs.

Les ordres de diversité et de gain de réseau pour diverses configurations peuvent être dérivés analytiquement [1, p. 86 - 100] et réduire à un tableau [1, p. 101] à la fois pour le cas où le canal est inconnu (CU - Canal inconnu) et pour le cas où le canal est connu (CK - Canal non connu) sur le côté de l'émetteur.

La configuration	Ordonnance sur la diversité	Gain de tableau
SIMO (CU, Rx-MRC)
SIMO (CK, Rx-MRC)
MISO (CU, OSTBC)		1
MISO (CK, Tx-MRC)
MIMO (CU, OSTBC)
MIMO (CK, DET)

D'accord, même avec des traits larges, mais maintenant nous avons au moins une certaine compréhension des aspects théoriques de la suppression de la décoloration. La question suivante est de savoir comment atteindre ces limites théoriques? Quelles sont les techniques d'activation des gains considérés?

Solution n ° 1. Codes temps spatiaux

L'une des classes de solutions de diversité spatiale les plus populaires est peut-être la classe des codes spatio-temporels (codes spatio-temporels). Par exemple, la méthode familière, je pense, de nombreux Alamouti (un exemple de code de bloc) [2, p. 40-46]:

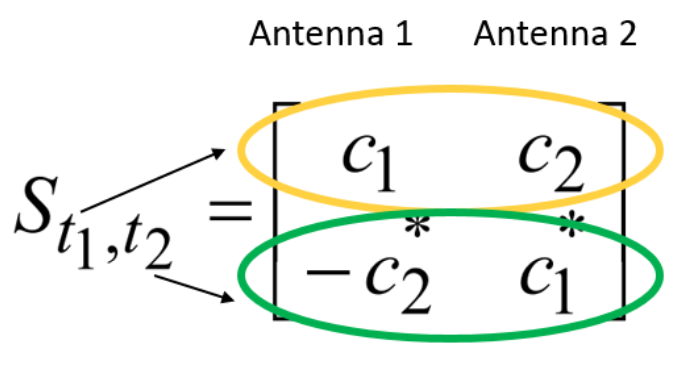
où c_i à i = 1,2 Y a-t-il des caractères saisis t_i à i = 1,2 Sont des plages horaires et $\ mathbf {S}$ - il s'agit en fait d'une matrice de codage.

Le schéma Alamouti est orthogonal [1, pp. 93-95, 97-98] et, surtout, ne nécessite pas d' informations sur l'état du canal.

La description mathématique de la transmission du signal codé par le schéma Alamouti, ainsi que plusieurs exemples de modélisation de cette technique dans MatLab se trouvent dans mon référentiel . Intéressé par bienvenue!

Cependant, comme vous pouvez le voir, le circuit d'Alamouti est un cas où nous n'avons que deux antennes d'émission ( M_T = 2 )
Mais ne vous découragez pas à l'avance: bien sûr, d'autres options sont disponibles, elles sont simplement appelées un peu différemment. Par exemple, selon [3], on peut appliquer les schémas de codage suivants:

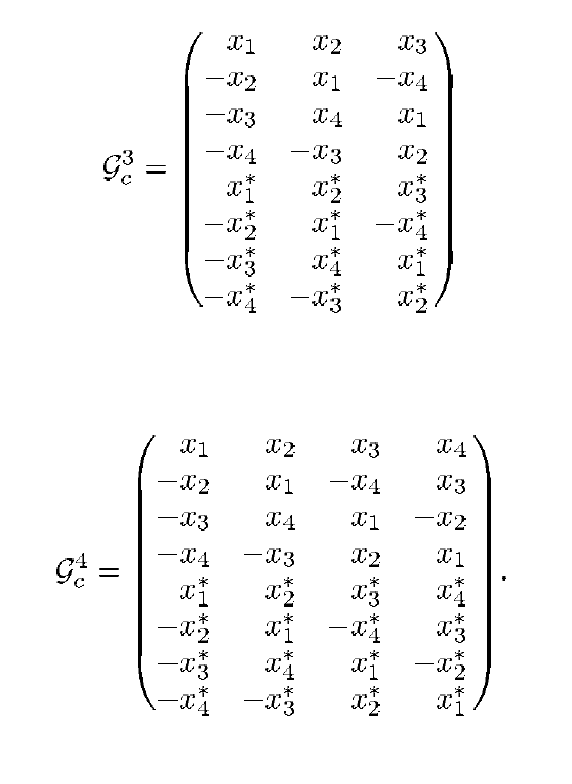
Fig. 2. Mécanismes de transfert des cas et [2].

Et il existe de nombreuses autres options: juste pour répondre aux conditions d'orthogonalité.

De tels codes nécessitent, en effet, les mêmes procédures de codage et de décodage que pour le code Alamouti. Par conséquent, ils sont généralement combinés sous le terme général de codes de blocs spatio-temporels orthogonaux (OSTBC - Codes de blocs spatio-temporels orthogonaux ).

Une grande attention est accordée à cette classe de codes dans les matériaux "Introduction aux systèmes MIMO" de MathWorks. Je conseille vivement à toutes les personnes intéressées de le lire!

Quel est le prix?

Comme le montre le schéma de transmission, bien que nous transmettions des symboles en parallèle, nous y consacrons plusieurs tranches de temps. Par conséquent, nous sacrifions la bande passante (au moins, nous l'obtenons moins). Pour le schéma Alamouti, un tel compromis est symétrique: on utilise 2 antennes et 2 tranches de temps (comme si on utilisait SISO en termes de bande passante). D'autres schémas peuvent affecter encore plus la vitesse de transmission.

Décision numéro 2. DET: transmission en mode propre dominant

Eh bien, pour la classe de techniques précédente, la connaissance de la chaîne n'était pas importante pour nous. Mais que faire si nous avons encore cette connaissance? Existe-t-il des techniques plus appropriées dans ce cas?

Dans l' un de mes articles précédents, nous avons discuté du fait que, connaissant l'état du canal, nous pouvons appliquer diverses méthodes de traitement du signal pour augmenter le débit. Le même principe fonctionne pour augmenter l'immunité au bruit.

Beaucoup ont probablement entendu parler de la méthode MRC et beaucoup savent que cette méthode convient très bien au cas SIMO , quand il y a au moins une antenne sur la transmission, mais il y en a encore beaucoup, ce qui signifie qu'il y a quelque chose à combiner.

Mais, probablement, déjà un plus petit nombre de lecteurs ont rencontré MRC du côté de la transmission (Tx-MRC) [1, p. 95,96], et encore moins avec la technologie DET (Dominant Eigenmode Transmission) [1, p. 98-100]. Réparez-le!

Pour commencer, considérons le cas général du canal MIMO et la dernière de ces méthodes - DET.

Quelle est l'essence de:

Si l'émetteur a une matrice $\ mathbf {H}$ alors il peut être traité.
Par exemple, décomposez-le via SVD : $\ mathbf {H} = \ mathbf {U} \ mathbf {\ Sigma} \ mathbf {V} ^ H$ obtenant ainsi plusieurs matrices d'une certaine propriété.
Ces propriétés peuvent être utilisées pour optimiser le transfert, par exemple en utilisant un pré-codage (pré-codage).

Nous introduisons un vecteur de pré-codage:

$\ underset {M_T \ times1} {\ mathbf {w}} = \ sqrt {M_T} \ underset {M_T \ times1} {\ mathbf {v} _1}$

où $\ mathbf {v} _1$ Est le premier vecteur de matrice (dominant, pour ainsi dire) $\ mathbf {V}$ .

De plus, nous pouvons également écrire le vecteur de post-traitement:

$\ underset {M_R \ times1} {\ mathbf {g}} = \ underset {M_R \ times1} {\ mathbf {u} _1}$

où $\ mathbf {u} _1$ Est le premier vecteur de la matrice $\ mathbf {U}$ .

Redéfinissez le modèle du signal reçu (voir le sujet de la bande passante ):

${z} = \ underset {1 \ times M_R} {\ mathbf {g} ^ H} \ underset {M_R \ times 1} {\ mathbf {y}} = \ mathbf {g} ^ H \ sqrt {\ frac { E_s} {M_T}} \ mathbf {H} \ mathbf {w} s + \ mathbf {g} ^ H \ mathbf {n} = \ sqrt {E_s} \ mathbf {u} _1 ^ H \ mathbf {H} \ mathbf {v} _1 s + \ hat {\ mathbf {n}} = \ sqrt {E_s} \ sigma_ {max} s + \ hat {\ mathbf {n}}$

Voila! La magie de l'algèbre linéaire a distingué parmi tous les chemins de distribution les plus rentables et y a dirigé toute l'énergie. En fait, nous avons devant nous un algorithme de formation de faisceau linéaire.

Au détriment de cette approche, tout comme dans le cas de OSTBC, la limitation de la bande passante est. Certes, cela se produit maintenant uniquement dans le domaine spatial.

Pourquoi la méthode contient-elle des valeurs propres dans son nom si nous ne parlions que de singulières?

Parce que les valeurs propres (cardinalité des chemins de propagation - évanouissement) peuvent être directement dérivées de nombres singuliers (amplitudes d'évanouissement):

$\ mathbf {R} _ {\ mathbf {HH} ^ H} = \ mathbf {HH} ^ H = \ mathbf {Q} \ mathbf {\ Lambda} \ mathbf {Q} ^ H = \ mathbf {Q} \ begin {bmatrix} \ lambda_ {max} & & & & \\ &. & & & \\ & &. & & \\ & & &. & \\ & & & & \ lambda_ {min} \\ \ end {bmatrix} \ mathbf {Q} ^ H$

Eh bien, avec le DET, il est plus ou moins clair ce qui est avec Tx-MRC?

C’est encore plus facile avec lui - c’est un cas particulier du DET, et maintenant nous allons le prouver.

Pour Tx-MRC, le vecteur de précodage suivant est proposé dans la littérature:

$\ mathbf {w} = \ sqrt {M_T} \ frac {\ mathbf {h} ^ H} {\ sqrt {|| \ mathbf {h} || ^ 2_F}}$

Nous gardons à l'esprit que le carré de la norme de Frobenius est égal à la valeur propre et, par conséquent, le carré du nombre singulier $|| \ mathbf {h} || ^ 2_F = \ lambda_ {max} = \ sigma ^ 2_ {max}$ (dans le cas de SIMO et MISO).

Ensuite, nous redéfinissons le modèle du signal reçu, uniquement pour le cas MISO:

$y = \ sqrt {\ frac {E_s} {M_T}} \ mathbf {h} \ mathbf {w} s + \ mathbf {n} = \ sqrt {\ frac {E_s} {M_T}} \ mathbf {h} \ sqrt {M_T} \ frac {\ mathbf {h} ^ H} {\ sqrt {|| \ mathbf {h} || ^ 2_F}} s + \ mathbf {n}} = \ frac {\ sqrt {E_s}} {\ sigma_ {max}} \ mathbf {h} \ mathbf {h} ^ H s + \ mathbf {n}} = \ frac {\ sqrt {E_s}} {\ sigma_ {max}} || \ mathbf {h } || _F ^ 2 s + \ mathbf {n}} = \ frac {\ sqrt {E_s}} {\ sigma_ {max}} \ lambda_ {max} s + \ mathbf {n}} = \ sqrt {E_s} \ sigma_ {max} s + \ mathbf {n}}$

Ce qui devait prouver.

Remarquez, maintenant nous ne parlons pas seulement de la séparation des signaux du côté émission et de leur combinaison du côté réception, comme ce fut le cas avec OSTBC. Maintenant, nous parlons de la distribution optimale de l'énergie. Cela signifie que les valeurs de gain de tableau dans ce cas sont supérieures à celles de OSTBC.

Maintenant que tous les mots ont été prononcés, nous allons essayer de simuler nos techniques.

Modélisation

Aujourd'hui, j'ai compté un peu: pour la modélisation OSTBC , des objets prêts à l'emploi de la Communication Toolbox ont été utilisés (MatLab R2014a - lequel c'était):

comm.OSTBCEncoder - Encodeur de codes de blocs spatio-temporels orthogonaux;
comm.OSTBCCombiner - Combinateur de codes de blocs spatio-temporels orthogonaux.

Pour la modulation et la démodulation (et le calcul d'erreur sur les bits - BER), les fonctions n'étaient plus utilisées, mais des fonctions . Leurs analogues se trouvent dans le package de communication Octave.

Les codes source peuvent être trouvés ici.

clear all; close all; clc snapshots = 100000; EbNo = 0:15; M = 2; % modulation order (BPSK) Mt = 2; % num. of Tx antennas Mr = [1; 2]; % num. of Rx antennas ostbcEnc = comm.OSTBCEncoder('NumTransmitAntennas', Mt); % for Alamouti ric_ber = zeros(length(EbNo), length(M), length(Mr)); sum_BER_alam = zeros(length(EbNo), length(M), length(Mr)); sum_BER_det = zeros(length(EbNo), length(M), length(Mr)); for mr = 1:length(Mr) ostbcComb = comm.OSTBCCombiner('NumTransmitAntennas', Mt, 'NumReceiveAntennas', Mr(mr)); H = zeros(Mr(mr), Mt, snapshots); alam_fad_msg = zeros(snapshots, Mr(mr)); for m = 1:length(M) ric_ber(:,m,mr) = berfading(EbNo, 'psk', M(m), Mr(mr)*Mt, 0); snr = EbNo+10*log10(log2(M(m))); % Signal-to-Noise Ratio message = randi([0, M(m)-1],100000,1); mod_msg = pskmod(message, M(m), 0, 'gray'); Es = mean(abs(mod_msg).^2); % symbol energy alam_msg = step(ostbcEnc, mod_msg); % OSTBC encoding % Channel h = (1/sqrt(2))*(randn(Mr(mr),Mt,snapshots/Mt)... + 1j*randn(Mr(mr),Mt, snapshots/Mt)); % Rayleigh flat fading % Channel is stable during to time-slots: H(:,:,1:2:end-1) = h; H(:,:,2:2:end) = h; pathGainself = permute(H,[3,2,1]); % Transmit through the channel (Alamouti): for q = 1:snapshots; alam_fad_msg(q,:) = (sqrt(Es/Mt)*H(:,:,q)*alam_msg(q,:).').'; end % DET: sigmas = zeros(length(mod_msg), 1); for hi = 1:length(mod_msg) [U, Sigma, Vh] = svd(H(:, :, hi)); sigmas(hi) = Sigma(1, 1); end det_fad_msg = mod_msg.*sigmas; No = Es./((10.^(EbNo./10))*log2(M(m))); % Noise spectrum density for c = 1:500 for jj = 1:length(EbNo) alam_noisy_msg = alam_fad_msg + ... sqrt(No(jj)/2)*(randn(size(alam_fad_msg)) + ... 1j*randn(size(alam_fad_msg))); % AWGN alam_decodeData = step(ostbcComb,alam_noisy_msg,pathGainself); %OSTBC combining alam_demod_msg = pskdemod(alam_decodeData, M(m), 0, 'gray'); % demodulation [number,alam_BER(c,jj)] = biterr(message, alam_demod_msg); % BER det_noisy_msg = det_fad_msg+ ... sqrt(No(jj)/2)*(randn(size(mod_msg)) + ... 1j*randn(size(mod_msg))); %AWGN det_decodeData = det_noisy_msg./sigmas; % Zero-Forcing equalization det_demod_msg = pskdemod(det_decodeData, M(m), 0, 'gray'); % demodulation [number,det_BER(c,jj)] = biterr(message, det_demod_msg); % BER end end sum_BER_alam(:,m, mr) = sum(alam_BER)./c; sum_BER_det(:,m, mr) = sum(det_BER)./c; end end figure(1) semilogy(EbNo, sum_BER_alam(:, 1, 1), 'b-o', ... EbNo, sum_BER_det(:,1,1), 'b->',... EbNo, ric_ber(:,1,1), 'b-',... EbNo, sum_BER_alam(:, 1, 2), 'r-o', ... EbNo, sum_BER_det(:,1,2), 'r->',... EbNo, ric_ber(:,1,2), 'r-',... 'LineWidth', 1.5) title('BPSK (Rayleigh flat fading)') legend('Alamouti (2x1)','Tx-MRC (2x1)','2-nd order diversity', ... 'Alamouti (2x2)','DET (2x2)','4-th order diversity') xlabel('EbNo (dB)') ylabel('BER') grid on

Il devrait en résulter quelque chose comme ceci:

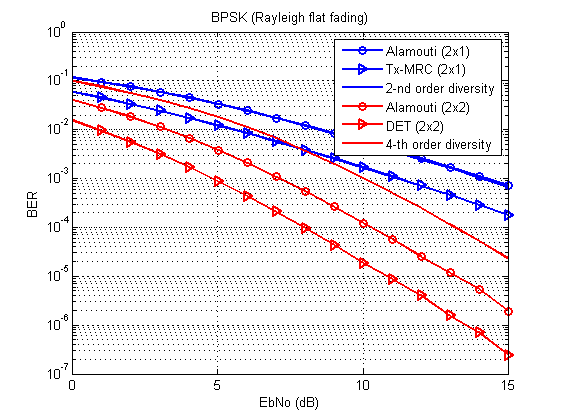
Fig. 3. Courbes d'erreur bit / symbole pour différentes techniques de transmission (BPSK, canal Rayleigh avec évanouissement plat). Comparer avec [1, p. 96, 100].

Et maintenant la question est: où est la courbe de la frontière théorique de la diversité du second ordre?

La réponse

Tout est conforme au tableau: cette courbe coïncide complètement avec l'Alamouti 2x1. Dans le cas de MIMO, le gain de matrice entre également en jeu et les courbes sont donc séparées.

D'une manière ou d'une autre, le DET (ou Tx-MRC) devrait surpasser l'Alamouti en qualité.

Comme ça: la connaissance c'est le pouvoir!

Littérature

Paulraj, Arogyaswami, Rohit Nabar et Dhananjay Gore. Introduction aux communications sans fil spatio-temporelles. Cambridge University Press, 2003.
Bakulin M. G., Varukina L. A., Kreindelin V. B. Technologie MIMO: principes et algorithmes // M.: Hot line - Telecom. - 2014 .-- T. 244.
Tarokh, V., Jafarkhani, H., et Calderbank, AR (1999). Codes de bloc spatio-temporels de conceptions orthogonales. Transactions IEEE sur la théorie de l'information, 45 (5), 1456-1467.

Au corps enseignant et à la fraternité étudiante de ma profession natale, je dis bonjour!

Diversité spatiale MIMO: Alamouti, DET et autre diversité spatiale

Ordre de diversité d'espace et gain de réseau

Solution n ° 1. Codes temps spatiaux

Décision numéro 2. DET: transmission en mode propre dominant

Modélisation

Littérature

More articles: