Introduction à l'apprentissage automatique

Le cours complet de russe se trouve sur ce lien .
Le cours d'anglais original est disponible sur ce lien .



De nouvelles conférences sont prévues tous les 2-3 jours.

Entretien avec Sebastian Trun, PDG Udacity

"Bonjour encore, je suis Paige et vous êtes mon invité aujourd'hui, Sebastian."
- Salut, je suis Sebastian!
- ... un homme qui a une carrière incroyable, qui a réussi à faire beaucoup de choses incroyables! Vous êtes co-fondateur d'Udacity, vous avez fondé Google X, vous êtes professeur à Stanford. Vous avez fait des recherches incroyables et un apprentissage approfondi tout au long de votre carrière. Qu'est-ce qui vous a apporté le plus de satisfaction et dans quels domaines avez-vous reçu le plus de récompenses pour le travail accompli?
- Franchement, j'aime vraiment être dans la Silicon Valley! J'aime être près de gens beaucoup plus intelligents que moi, et j'ai toujours considéré la technologie comme un outil qui change les règles du jeu de diverses manières - de l'éducation à la logistique, aux soins de santé, etc. Tout cela change si vite, et il y a une incroyable envie de participer à ces changements, de les observer. Vous regardez votre environnement et comprenez que la plupart de ce que vous voyez autour de vous ne fonctionne pas comme il se doit - vous pouvez toujours inventer quelque chose de nouveau!
- Eh bien, c'est une vision très optimiste de la technologie! Quelle a été la plus grande eureka de votre carrière?
- Seigneur, il y en avait tellement! Je me souviens d'un des jours où Larry Page m'a appelé et m'a suggéré de créer des voitures à pilote automatique qui pourraient traverser toutes les rues de Californie. À ce moment-là, j'étais considéré comme un expert, j'étais classé parmi ceux-là et j'étais la personne même qui disait "non, cela ne peut pas être fait". Après cela, Larry m'a convaincu que, en principe, il est possible de le faire, il suffit de commencer et d'essayer. Et nous l'avons fait! C'était le moment où j'ai réalisé que même les experts se trompaient et en disant «non», nous sommes 100% pessimistes. Je pense que nous devrions être plus ouverts au nouveau.
- Ou, par exemple, si Larry Page vous appelle et vous dit: «Hé, faites quelque chose de cool comme Google X» et vous obtenez quelque chose d'assez cool!
- Oui, c'est sûr, pas besoin de se plaindre! Je veux dire, tout cela est un processus qui passe par beaucoup de discussions sur le chemin de la mise en œuvre. J'ai vraiment de la chance de travailler et j'en suis fier, sur Google X et sur d'autres projets.
- Génial! Donc, ce cours est entièrement consacré à l'utilisation de TensorFlow. Avez-vous de l'expérience avec TensorFlow ou peut-être le connaissez-vous?
- Oui! J'adore littéralement TensorFlow, bien sûr! Dans mon propre laboratoire, nous l'utilisons souvent et beaucoup, l'un des travaux les plus importants basés sur TensorFlow a été publié il y a environ deux ans. Nous avons appris que l'iPhone et Android peuvent être plus efficaces pour détecter le cancer de la peau que les meilleurs dermatologues du monde. Nous avons publié nos recherches dans Nature et cela a créé une sorte d'agitation en médecine.
- Cela semble incroyable! Vous connaissez et aimez donc TensorFlow, ce qui est génial en soi! Avez-vous déjà travaillé avec TensorFlow 2.0?
- Non, malheureusement je n'ai pas encore eu le temps.
- Il sera juste incroyable! Tous les étudiants de ce cours travailleront avec cette version.
- Je les envie! Je vais certainement l'essayer!
- Génial! Dans notre cours, il y a beaucoup d'étudiants qui dans leur vie n'ont jamais été impliqués dans l'apprentissage automatique, du mot "complètement". Pour eux, le domaine peut être nouveau, peut-être pour quelqu'un qui se programme lui-même sera nouveau. Quels conseils leur donnez-vous?
- Je souhaite qu'ils restent ouverts - à de nouvelles idées, techniques, solutions, positions. L'apprentissage automatique est en fait plus facile que la programmation. Dans le processus de programmation, vous devez prendre en compte chaque cas dans les données source, adapter la logique du programme et les règles pour cela. En ce moment même, en utilisant TensorFlow et l'apprentissage automatique, vous formez essentiellement l'ordinateur à l'aide d'exemples, laissant l'ordinateur trouver les règles lui-même.
- C'est incroyablement intéressant! J'ai hâte d'en dire un peu plus sur l'apprentissage automatique aux étudiants de ce cours! Sebastian, merci d'avoir pris le temps de venir nous voir aujourd'hui!
- Merci! Restez en contact!

Qu'est-ce que l'apprentissage automatique?

Commençons donc par la tâche suivante - des valeurs d'entrée et de sortie données.



Lorsque vous avez la valeur 0 comme valeur d'entrée, puis 32 comme valeur de sortie Lorsque vous avez 8 comme valeur d'entrée, puis 46,4 comme valeur de sortie. Lorsque vous avez 15 comme valeur d'entrée, puis 59 comme valeur de sortie, etc.

Examinez ces valeurs de plus près et laissez-moi vous poser une question. Pouvez-vous déterminer quelle sera la sortie si nous obtenons 38 à l'entrée?



Si vous avez répondu 100,4, vous aviez raison!



Alors, comment pourrions-nous résoudre ce problème? Si vous regardez attentivement les valeurs, vous pouvez voir qu'elles sont liées par l'expression:



Où C - degrés Celsius (valeurs d'entrée), F - Fahrenheit (valeurs de sortie).

Ce que votre cerveau vient de faire - a comparé les valeurs d'entrée et les valeurs de sortie et a trouvé un modèle commun (connexion, dépendance) entre elles - c'est ce que fait l'apprentissage automatique.

Sur la base des valeurs d'entrée et de sortie, les algorithmes d'apprentissage automatique trouveront un algorithme approprié pour convertir les valeurs d'entrée en valeurs de sortie. Cela peut être représenté comme suit:



Regardons un exemple. Imaginez que nous voulons développer un programme qui convertira les degrés Celsius en degrés Fahrenheit en utilisant la formule F = C * 1.8 + 32 .



La solution, à l'approche du point de vue du développement logiciel traditionnel, peut être implémentée dans n'importe quel langage de programmation en utilisant la fonction:



Alors qu'avons-nous? La fonction prend une valeur d'entrée de C, puis calcule la valeur de sortie de F à l'aide d'un algorithme explicite, puis renvoie la valeur calculée.



D'un autre côté, dans l'approche d'apprentissage automatique, nous n'avons que des valeurs d'entrée et de sortie, mais pas l'algorithme lui-même:



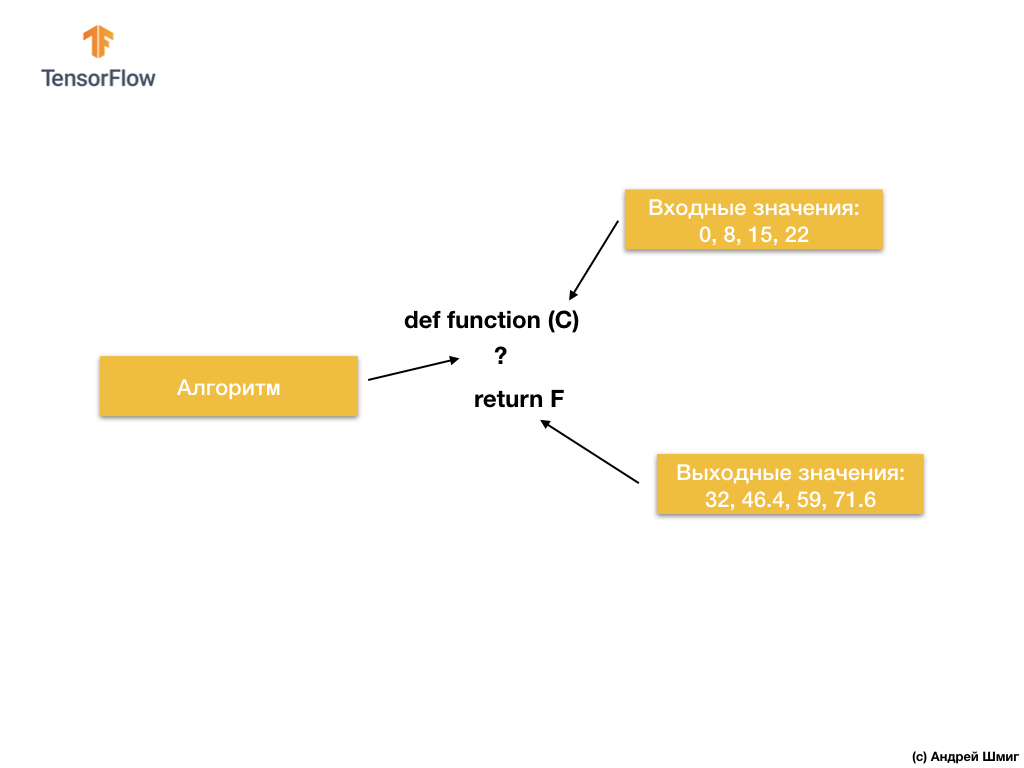
L'approche d'apprentissage automatique repose sur l'utilisation de réseaux de neurones pour trouver la relation entre les valeurs d'entrée et de sortie.



Vous pouvez considérer les réseaux de neurones comme une pile de couches, chacune étant constituée de mathématiques (formules) et de variables internes précédemment connues. La valeur d'entrée pénètre dans le réseau neuronal et traverse une pile de couches de neurones. En passant à travers les couches, la valeur d'entrée est convertie selon les mathématiques (formules données) et les valeurs des variables internes des couches, produisant une valeur de sortie.

Pour que le réseau de neurones puisse apprendre et déterminer la relation correcte entre les valeurs d'entrée et de sortie, nous devons le former - le former.

Nous formons le réseau neuronal par des tentatives répétées de faire correspondre les valeurs d'entrée à celles de sortie.



Dans le processus de formation, l'ajustement (sélection) des valeurs des variables internes dans les couches du réseau neuronal a lieu jusqu'à ce que le réseau apprenne à générer les valeurs de sortie correspondantes aux valeurs d'entrée correspondantes.

Comme nous le verrons plus loin, afin de former un réseau de neurones et lui permettre de sélectionner les valeurs les plus adaptées des variables internes, des milliers ou des dizaines de milliers d'itérations (formations) sont effectuées.



En tant que version simplifiée de la compréhension de l'apprentissage automatique, vous pouvez imaginer des algorithmes d'apprentissage automatique comme des fonctions qui sélectionnent les valeurs des variables internes afin que les valeurs d'entrée correctes correspondent aux valeurs de sortie correctes.

Il existe de nombreux types d'architectures de réseaux de neurones. Cependant, quelle que soit l'architecture que vous choisissez, les calculs à l'intérieur (quels calculs sont effectués et dans quel ordre) resteront inchangés pendant la formation. Au lieu de changer les mathématiques, les variables internes (poids et décalages) changent pendant l'entraînement.

Par exemple, dans la tâche de conversion de degrés Celsius en degrés Fahrenheit, le modèle commence par multiplier la valeur d'entrée par un certain nombre (poids) et en ajoutant une autre valeur (décalage). La formation aux modèles consiste à trouver des valeurs adaptées à ces variables, sans modifier les opérations de multiplication et d'addition effectuées.

Mais une chose sympa à penser! Si vous avez résolu le problème de la conversion des degrés Celsius en Fahrenheit, ce qui est indiqué dans la vidéo et dans le texte ci-dessous, vous l'avez probablement résolu parce que vous aviez une expérience ou des connaissances sur la façon d'effectuer ce type de conversion des degrés Celsius en Fahrenheit. Par exemple, vous savez peut-être que 0 degré Celsius correspond à 32 degrés Fahrenheit. D'un autre côté, les systèmes basés sur l'apprentissage automatique ne disposent pas de connaissances préalables pour résoudre le problème. Ils apprennent à résoudre de tels problèmes sans se baser sur des connaissances antérieures et en leur absence totale.

Assez parlé - passez à la partie pratique de la conférence!

CoLab: convertir des degrés Celsius en degrés Fahrenheit

La version russe du code source CoLab et la version anglaise du code source CoLab .

Les bases: apprendre le premier modèle

Bienvenue à CoLab, où nous formerons notre premier modèle d'apprentissage automatique!

Nous essaierons de maintenir la simplicité du matériel présenté et n'introduirons que les concepts de base nécessaires au travail. Les CoLabs ultérieurs contiendront des techniques plus avancées.

La tâche que nous allons résoudre est la conversion des degrés Celsius en degrés Fahrenheit. La formule de conversion est la suivante:

$$

$$f = c \ fois 1,8 + 32$$

Bien sûr, il serait plus facile d'écrire simplement une fonction de conversion en Python ou tout autre langage de programmation qui effectuerait des calculs directs, mais dans ce cas, ce ne serait pas de l'apprentissage automatique :)

Au lieu de cela, nous introduisons dans l'entrée TensorFlow nos degrés d'entrée disponibles Celsius (0, 8, 15, 22, 38) et leurs degrés Fahrenheit correspondants (32, 46, 59, 72, 100). Ensuite, nous formerons le modèle de manière à ce qu'il corresponde approximativement à la formule ci-dessus.

Importer les dépendances

La première chose que nous importons est TensorFlow . Ici et dans ce qui suit, nous l'appelons abrégé tf . Nous configurons également le niveau de journalisation - uniquement les erreurs.

Ensuite, importez NumPy tant que np . Numpy nous aide à présenter nos données sous forme de listes performantes.

 from __future__ import absolute_import, division, print_function, unicode_literals import tensorflow as tf tf.logging.set_verbosity(tf.logging.ERROR) import numpy as np 

Préparation des données de formation

Comme nous l'avons vu précédemment, la technique d'apprentissage automatique avec l'enseignant est basée sur la recherche d'un algorithme pour convertir les données d'entrée en sortie. Étant donné que la tâche de ce CoLab est de créer un modèle pouvant produire le résultat de la conversion des degrés Celsius en degrés Fahrenheit, nous créerons deux listes - celsius_q et fahrenheit_a , que nous utilisons lors de la formation de notre modèle.

 celsius_q = np.array([-40, -10, 0, 8, 15, 22, 38], dtype=float) fahrenheit_a = np.array([-40, 14, 32, 46, 59, 72, 100], dtype=float) for i,c in enumerate(celsius_q): print("{}   = {}  ".format(c, fahrenheit_a[i])) 

-40.0 = -40.0
-10.0 = 14.0
0.0 = 32.0
8.0 = 46.0
15.0 = 59.0
22.0 = 72.0
38.0 = 100.0

Quelques terminologies d'apprentissage automatique:

• La propriété est la ou les valeurs d'entrée de notre modèle. Dans ce cas, la valeur unitaire est le degré Celsius.
• Les étiquettes sont les valeurs de sortie que notre modèle prédit. Dans ce cas, la valeur unitaire est le degré Fahrenheit.
• Un exemple est une paire de valeurs d'entrée-sortie utilisées pour la formation. Dans ce cas, il s'agit d'une paire de valeurs de celsius_q et fahrenheit_a sous un certain indice, par exemple (22,72).

Créer un modèle

Ensuite, nous créons un modèle. Nous utiliserons le modèle le plus simplifié - le modèle d'un réseau entièrement connecté (réseau Dense ). Étant donné que la tâche est assez triviale, le réseau sera également constitué d'une seule couche avec un seul neurone.

Construire un réseau

Nous nommerons la couche l0 ( l ayer et zéro) et la créerons en initialisant tf.keras.layers.Dense avec les paramètres suivants:

• input_shape=[1] - ce paramètre détermine la dimension du paramètre d'entrée - une valeur unique. Matrice 1 × 1 avec une seule valeur. Comme il s'agit de la première (et unique) couche, la dimension des données d'entrée correspond à la dimension de l'ensemble du modèle. La seule valeur est une valeur à virgule flottante représentant les degrés Celsius.
• units=1 - ce paramètre détermine le nombre de neurones dans la couche. Le nombre de neurones détermine le nombre de variables de la couche interne qui seront utilisées pour s'entraîner à trouver une solution au problème. Comme il s'agit de la dernière couche, sa dimension est égale à la dimension du résultat - la valeur de sortie du modèle - un seul nombre à virgule flottante représentant les degrés Fahrenheit. (Dans un réseau multicouche, la taille et la forme de la couche input_shape doivent correspondre à la taille et à la forme de la couche suivante).

 l0 = tf.keras.layers.Dense(units=1, input_shape=[1]) 

Convertir les calques en modèle

Une fois les couches définies, elles doivent être converties en modèle. Sequential modèle Sequential prend comme arguments la liste des couches dans l'ordre dans lequel elles doivent être appliquées - de la valeur d'entrée à la valeur de sortie.

Notre modèle n'a qu'une seule couche - l0 .

 model = tf.keras.Sequential([l0]) 

Remarque
Très souvent, vous rencontrerez la définition des couches directement dans la fonction de modèle, plutôt que leur description préliminaire et leur utilisation ultérieure:

 model = tf.keras.Sequential([ tf.keras.layers.Dense(units=1, input_shape=[1]) ]) 

Nous compilons un modèle avec une fonction de perte et d'optimisation

Avant la formation, le modèle doit être compilé (assemblé). Lors de la compilation pour la formation, vous avez besoin de:

• fonction de perte - un moyen de mesurer la distance entre la valeur prédite et la valeur de sortie souhaitée (une différence mesurable est appelée «perte»).
• fonction d'optimisation - un moyen d'ajuster les variables internes pour réduire les pertes.

 model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) 

La fonction de perte et la fonction d'optimisation sont utilisées lors de l'apprentissage du modèle ( model.fit(...) mentionné ci-dessous) pour effectuer des calculs initiaux à chaque point puis optimiser les valeurs.

L'action de calculer les pertes actuelles et l'amélioration ultérieure de ces valeurs dans le modèle est exactement ce qu'est la formation (une itération).

Pendant la formation, la fonction d'optimisation est utilisée pour calculer les ajustements des valeurs des variables internes. Le but est d'ajuster les valeurs des variables internes de cette manière dans le modèle (et c'est en fait une fonction mathématique) afin qu'elles reflètent le plus fidèlement possible l'expression existante pour convertir les degrés Celsius en degrés Fahrenheit.

TensorFlow utilise l'analyse numérique pour effectuer ce type d'opérations d'optimisation, et toute cette complexité est cachée à nos yeux, nous n'entrerons donc pas dans les détails de ce cours.

Ce qu'il est utile de savoir sur ces options:

La fonction de perte (erreur standard) et la fonction d'optimisation (Adam) utilisées dans cet exemple sont standard pour ces modèles simples, mais de nombreux autres sont disponibles en plus d'eux. À ce stade, nous ne nous soucions pas du fonctionnement de ces fonctions.

Ce à quoi vous devez faire attention, c'est la fonction d'optimisation et le paramètre est le coefficient de learning rate , qui dans notre exemple est 0.1 . Il s'agit de la taille de pas utilisée lors du réglage des valeurs internes des variables. Si la valeur est trop petite, il faudra trop d'itérations de formation pour former le modèle. Trop - la précision baisse. Trouver une bonne valeur pour le coefficient de taux d'apprentissage nécessite quelques essais et erreurs; il se situe généralement dans la plage de 0.01 (par défaut) à 0.1 .

Nous formons le modèle

La formation du modèle est réalisée par méthode d' fit .

Pendant l'entraînement, le modèle reçoit des degrés Celsius à l'entrée, effectue des transformations en utilisant les valeurs des variables internes (appelées «poids») et renvoie des valeurs qui doivent correspondre aux degrés Fahrenheit. Comme les valeurs initiales des poids sont fixées arbitrairement, les valeurs résultantes seront loin des valeurs correctes. La différence entre le résultat souhaité et le réel est calculée à l'aide de la fonction de perte, et la fonction d'optimisation détermine comment les poids doivent être ajustés.

Ce cycle de calculs, de comparaisons et d'ajustements est contrôlé dans le cadre de la méthode d' fit . Le premier argument est la valeur d'entrée, le deuxième argument est la valeur de sortie souhaitée. L'argument des epochs détermine combien de fois ce cycle de formation doit être terminé. L'argument verbose contrôle le niveau de journalisation.

 history = model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) print("  ") 

Dans les vidéos suivantes, nous allons plonger dans les détails de la façon dont tout cela fonctionne et comment exactement les couches entièrement connectées (couches Dense ) "sous le capot".

Afficher les statistiques de formation

La méthode fit renvoie un objet qui contient des informations sur les modifications des pertes à chaque itération suivante. Nous pouvons utiliser cet objet pour créer un programme de perte approprié. Une perte élevée signifie que les degrés Fahrenheit prédits par le modèle sont loin des vraies valeurs du tableau fahrenheit_a .

Pour la visualisation, nous utiliserons Matplotlib . Comme vous pouvez le voir, notre modèle s'améliore très rapidement au tout début, puis arrive à une amélioration stable et lente jusqu'à ce que les résultats deviennent «presque» parfaits à la toute fin de la formation.

 import matplotlib.pyplot as plt plt.xlabel('Epoch') plt.ylabel('Loss') plt.plot(history.history['loss']) 

Nous utilisons le modèle pour les prédictions.

Nous avons maintenant un modèle qui a été formé sur les valeurs d'entrée celsius_q et les valeurs de sortie fahrenheit_a pour déterminer la relation entre elles. Nous pouvons utiliser la méthode de prédiction pour calculer les degrés Fahrenheit par lesquels nous ne connaissions pas auparavant les degrés Celsius correspondants.

Par exemple, combien coûte 100,0 degrés Celsius Fahrenheit? Essayez de deviner avant d'exécuter le code ci-dessous.

 print(model.predict([100.0])) 

Conclusion:

[[211.29639]]


La bonne réponse est 100 × 1,8 + 32 = 212, donc notre modèle a plutôt bien fonctionné!

Revue

• Nous avons créé un modèle en utilisant la couche Dense .
• Nous l'avons formée avec 3 500 exemples (7 paires de valeurs, 500 itérations d'entraînement)

Notre modèle a ajusté les valeurs des variables internes (poids) dans la couche Dense de manière à renvoyer les valeurs correctes de degrés Fahrenheit à une valeur d'entrée arbitraire de degrés Celsius.

Nous regardons les poids

Affichons les valeurs des variables internes de la couche Dense .

 print("   : {}".format(l0.get_weights())) 

Conclusion:

    : [array([[1.8261501]], dtype=float32), array([28.681389], dtype=float32)] 

La valeur de la première variable est proche de ~ 1,8 et la seconde de ~ 32. Ces valeurs (1,8 et 32) sont des valeurs directes dans la formule de conversion des degrés Celsius en degrés Fahrenheit.

C'est vraiment très proche des valeurs réelles de la formule! Nous examinerons ce point plus en détail dans les vidéos suivantes, où nous montrons comment fonctionne la couche Dense , mais pour l'instant, vous devez seulement savoir qu'un neurone avec une seule entrée et sortie contient des mathématiques simples - y = mx + b (comme une équation direct), qui n'est rien de plus que notre formule de conversion des degrés Celsius en degrés Fahrenheit, f = 1.8c + 32 .

Comme les représentations sont les mêmes, les valeurs des variables internes du modèle devraient converger vers celles présentées dans la formule réelle, ce qui s'est finalement produit.

Avec la présence de neurones supplémentaires, de valeurs d'entrée et de valeurs de sortie supplémentaires, la formule devient un peu plus compliquée, mais l'essence reste la même.

Un peu d'expérimentation

Pour le plaisir! Que se passe-t-il si nous créons plus de couches Dense avec plus de neurones, qui à leur tour contiendront plus de variables internes?

 l0 = tf.keras.layers.Dense(units=4, input_shape=[1]) l1 = tf.keras.layers.Dense(units=4) l2 = tf.keras.layers.Dense(units=1) model = tf.keras.Sequential([l0, l1, l2]) model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) print("  ") print(model.predict([100.0])) print(" ,  100    {}  ".format(model.predict([100.0]))) print("    l0: {}".format(l0.get_weights())) print("    l1: {}".format(l1.get_weights())) print("    l2: {}".format(l2.get_weights())) 

Conclusion:

    [[211.74748]]  ,  100    [[211.74748]]       l0: [array([[-0.5972079 , -0.05531882, -0.00833384, -0.10636603]], dtype=float32), array([-3.0981746, -1.8776944, 2.4708805, -2.9092448], dtype=float32)]     l1: [array([[ 0.09127654, 1.1659832 , -0.61909443, 0.3422218 ], [-0.7377194 , 0.20082018, -0.47870865, 0.30302727], [-0.1370897 , -0.0667181 , -0.39285263, -1.1399261 ], [-0.1576551 , 1.1161333 , -0.15552482, 0.39256814]], dtype=float32), array([-0.94946504, -2.9903848 , 2.9848468 , -2.9061244 ], dtype=float32)]     l2: [array([[-0.13567649], [-1.4634581 ], [ 0.68370366], [-1.2069695 ]], dtype=float32), array([2.9170544], dtype=float32)] 

Comme vous l'avez peut-être remarqué, le modèle actuel est également capable de prédire assez bien les degrés correspondants de Fahrenheit. Cependant, si nous regardons les valeurs des variables internes (poids) des neurones par couches, nous ne verrons aucune valeur similaire à 1,8 et 32. La complexité supplémentaire du modèle cache la forme «simple» de conversion des degrés Celsius en degrés Fahrenheit.

Restez connecté et dans la prochaine partie, nous verrons comment fonctionnent les couches denses «sous le capot».

Bref résumé

Félicitations! Vous venez de former votre premier modèle. En pratique, nous avons vu comment, par les valeurs d'entrée et de sortie, le modèle a appris à multiplier la valeur d'entrée par 1,8 et à y ajouter 32 pour obtenir le résultat correct.



C'était vraiment impressionnant, compte tenu du nombre de lignes de code dont nous avions besoin pour écrire:

 l0 = tf.keras.layers.Dense(units=1, input_shape=[1]) model = tf.keras.Sequential([l0]) model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) history = model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) model.predict([100.0]) 

L'exemple ci-dessus est un plan général pour tous les programmes d'apprentissage automatique. Vous utiliserez des constructions similaires pour créer et former des réseaux de neurones et pour résoudre des problèmes ultérieurs.

Processus de formation

Le processus de formation (qui se déroule dans la méthode model.fit(...)) consiste en une séquence très simple d'actions, dont le résultat devrait être les valeurs des variables internes donnant les résultats le plus près possible de l'original. Le processus d'optimisation par lequel ces résultats sont obtenus, appelé descente de gradient , utilise une analyse numérique pour trouver les valeurs les plus appropriées pour les variables internes du modèle.

Afin de vous engager dans l'apprentissage automatique, vous n'avez en principe pas besoin de comprendre ces détails. Mais pour ceux qui sont toujours intéressés à en savoir plus: la descente de gradient par itérations modifie un peu les valeurs des paramètres, les «tirant» dans la bonne direction jusqu'à ce que les meilleurs résultats soient obtenus. Dans ce cas, les «meilleurs résultats» (meilleures valeurs) signifient que toute modification ultérieure du paramètre ne fera qu'aggraver le résultat du modèle. Une fonction qui mesure le bien ou le mal d'un modèle à chaque itération est appelée «fonction de perte», et le but de chaque «traction» (ajustement des valeurs internes) est de réduire la valeur de la fonction de perte.

Le processus de formation commence par le bloc «distribution directe», dans lequel les paramètres d'entrée vont à l'entrée du réseau neuronal, suivent les neurones cachés et ensuite vont au week-end. Le modèle applique ensuite des transformations internes sur les valeurs d'entrée et les variables internes pour prédire la réponse.

Dans notre exemple, la valeur d'entrée est la température en degrés Celsius et le modèle a prédit la valeur correspondante en degrés Fahrenheit.



Dès que la valeur est prédite, la différence entre la valeur prédite et la bonne est calculée. La différence est appelée «perte» et est une forme de mesure de l'efficacité du modèle. La valeur de perte est calculée par la fonction de perte, que nous avons déterminée par l'un des arguments lors de l'appel de la méthode model.compile(...).

Après avoir calculé la valeur de perte, les variables internes (poids et déplacements) de toutes les couches du réseau neuronal sont ajustées pour minimiser la valeur de perte afin d'approximer la valeur de sortie à la valeur de référence initiale correcte.



Ce processus d'optimisation est appelé descente de gradient . Un algorithme d'optimisation spécifique est utilisé pour calculer une nouvelle valeur pour chaque variable interne lorsque la méthode est appelée model.compile(...). Dans l'exemple ci-dessus, nous avons utilisé un algorithme d'optimisation Adam.

Il n'est pas nécessaire de comprendre les principes du processus de formation pour ce cours, mais si vous êtes assez curieux, vous pouvez trouver plus d'informations sur le cours Google Crash(La traduction et la partie pratique de l'ensemble du cours sont définies dans les plans de publication de l'auteur).

À ce stade, vous devez déjà être familiarisé avec les termes suivants:

• Propriété : valeur d'entrée de notre modèle;
• Exemples : paires entrée + sortie;
• Tags : valeurs de sortie du modèle;
• Couches : une collection de nœuds réunis au sein d'un réseau de neurones;
• Modèle : représentation de votre réseau neuronal;
• Dense et entièrement connecté : chaque nœud d'une couche est connecté à chaque nœud de la couche précédente.
• Poids et décalages : modéliser les variables internes;
• Perte : la différence entre la valeur de sortie souhaitée et la valeur de sortie réelle du modèle;
• MSE : , , , .
• : , - ;
• : ;
• : «» ;
• : ;
• : ;
• : ;
• : , .

Dense-

, , .

. ? 3 , .



Rappelons qu'un réseau de neurones peut être imaginé comme un ensemble de couches, chacune composée de nœuds appelés neurones. Les neurones à chaque niveau peuvent être connectés aux neurones de chaque couche suivante. Le type de couches dans lequel chaque neurone d'une couche est connecté à l'autre neurone de la couche suivante est appelé une couche entièrement connectée (entièrement connectée) ou dense ( Dense-couche).



Ainsi, lorsque nous utilisons des couches entièrement connectées keras, nous informons en quelque sorte que les neurones de cette couche doivent être connectés à tous les neurones de la couche précédente.

Pour créer le réseau neuronal ci-dessus, les expressions suivantes nous suffisent:

 hidden = tf.keras.layers.Dense(units=2, input_shape=[3]) output = tf.keras.layers.Dense(units=1) model = tf.keras.Sequential([hidden, output]) 

Nous avons donc compris ce que sont les neurones et comment ils sont liés. Mais comment fonctionnent les couches entièrement connectées?

Pour comprendre ce qui se passe réellement là-bas et ce qu'ils font, nous devons regarder «sous le capot» et analyser les mathématiques internes des neurones.



Imaginez que notre modèle reçoive trois paramètres - 1, 2, 3, et 1, 2 3- les neurones de notre réseau. Rappelez-vous que nous avons dit qu'un neurone a des variables internes? Ainsi, w * et b * sont les mêmes variables internes d'un neurone, également appelées poids et déplacements. Ce sont les valeurs de ces variables qui sont ajustées dans le processus d'apprentissage pour obtenir les résultats les plus précis de comparaison des valeurs d'entrée à la sortie.



Ce que vous devez certainement garder à l'esprit, c'est que les mathématiques internes du neurone restent inchangées . En d'autres termes, pendant le processus de formation, seuls les poids et les déplacements changent .

Lorsque vous commencez à apprendre l'apprentissage automatique, cela peut sembler étrange - le fait que cela fonctionne vraiment, mais c'est ainsi que fonctionne l'apprentissage automatique!

Revenons à notre exemple de conversion des degrés Celsius en degrés Fahrenheit.



Avec un seul neurone, nous n'avons qu'un seul poids et un seul déplacement. Tu sais quoi? C'est exactement à quoi ressemble la formule de conversion des degrés Celsius en degrés Fahrenheit. Si nous substituons la w11valeur 1.8, et au lieu de b1- 32, nous obtenons le modèle de transformation final!

Si nous revenons aux résultats de notre modèle de la partie pratique, nous faisons attention au fait que les indicateurs de poids et de déplacement ont été «calibrés» de manière à correspondre approximativement aux valeurs de la formule.

Nous avons délibérément créé un tel exemple pratique afin de montrer clairement la comparaison exacte entre les poids et les décalages. En mettant l'apprentissage automatique en pratique, nous ne pouvons jamais comparer les valeurs des variables avec l'algorithme cible de cette manière, comme dans l'exemple ci-dessus. Comment pouvons-nous faire cela? Pas question, car nous ne connaissons même pas l'algorithme cible!

Pour résoudre les problèmes d'apprentissage automatique, nous testons diverses architectures de réseaux de neurones avec différents nombres de neurones - par essais et erreurs, nous trouvons les architectures et les modèles les plus précis et espérons qu'ils résoudront le problème dans le processus d'apprentissage. Dans la prochaine partie pratique, nous pourrons étudier des exemples spécifiques de cette approche.

Restez en contact, car le plaisir commence maintenant!

Résumé

Dans cette leçon, nous avons appris les approches de base de l'apprentissage automatique et appris comment fonctionnent les couches (couches Dense) entièrement connectées . Vous avez formé votre premier modèle à convertir des degrés Celsius en degrés Fahrenheit. Vous avez également appris les termes de base utilisés dans l'apprentissage automatique, tels que les propriétés, les exemples, les étiquettes. Vous avez, entre autres, écrit les principales lignes de code en Python, qui sont l'épine dorsale de tout algorithme d'apprentissage automatique. Vous avez vu qu'en quelques lignes de code, vous pouvez créer, former et demander une prédiction à partir d'un réseau de neurones en utilisant TensorFlowet Keras.

... et appel à l'action standard - inscrivez-vous, mettez un plus et partagez :)


YouTube: https://youtube.com/channel/ashmig
Télégramme: https://t.me/ashmig
VK: https://vk.com/ashmig