Il est bien connu que la plupart des séries chronologiques auxquelles un chercheur doit faire face ne sont pas stationnaires, et leur analyse est beaucoup plus compliquée que l'étude des processus stationnaires. Étant donné que l'intérêt pour les ondelettes semble s'être calmé, il est utile de discuter d'autres instruments «non stationnaires» qui sont utiles principalement pour estimer les fréquences instantanées, ainsi que pour évaluer les spectres instantanés.
Tout d'abord, il est logique de rappeler le «signal analytique». Ci-dessous, le «modèle An» fait référence à l'impédance et à la puissance instantanées du signal de test après achèvement de sa partie imaginaire (décalée en phase de π / 2).
Mais il n'est pas toujours possible de bricoler avec la transformation de Gilbert. Plus tôt, une méthode d'estimation spectrale autorégressive appropriée pour travailler avec des séquences courtes a déjà été
mentionnée . Ici, le «modèle AR» sera compris comme l'étude de courts fragments (de 5 échantillons) se chevauchant du signal d'origine afin de déterminer les coefficients d'autorégression de second ordre, en trouvant les «pôles» du modèle à partir d'eux, etc.
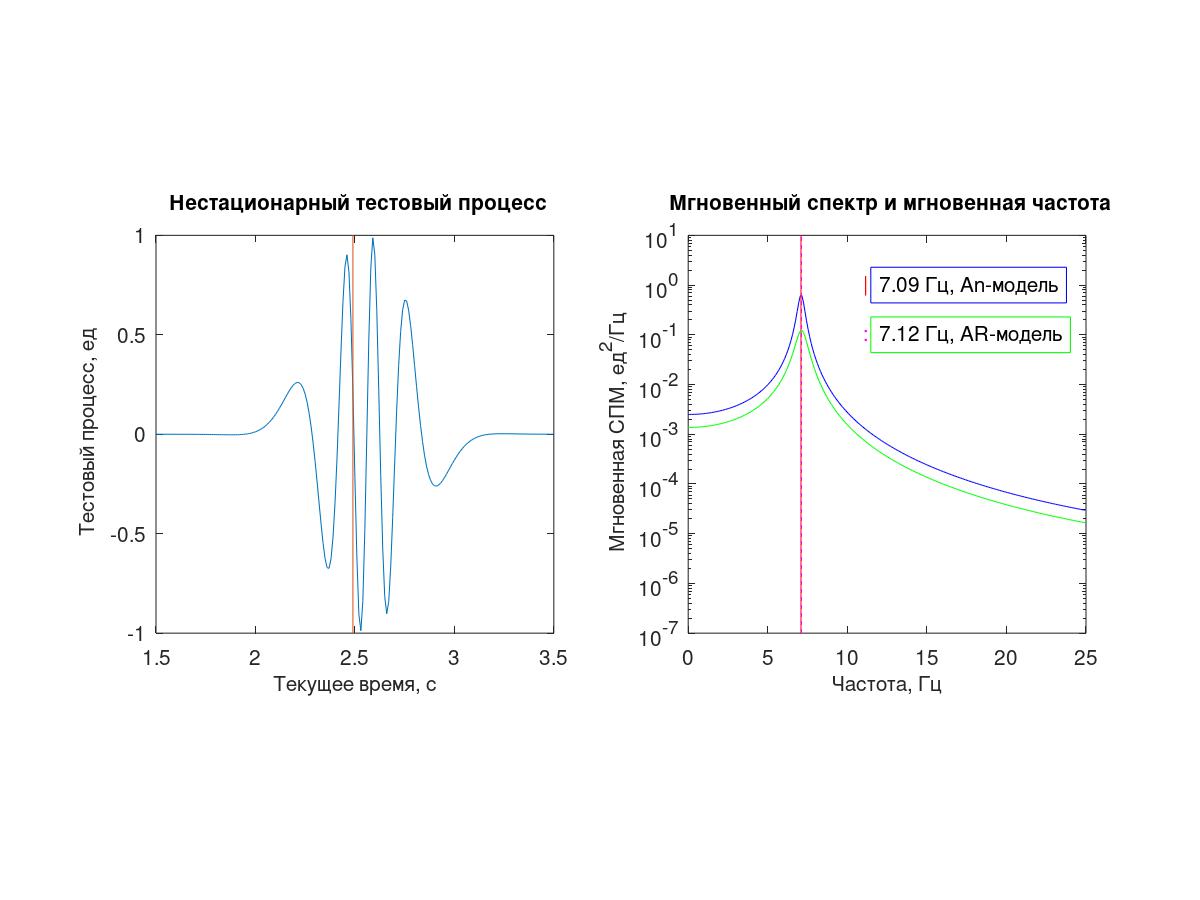

Les deux méthodes décrites ici reposent sur un principe - l'hypothèse selon laquelle, dans un petit voisinage du moment temporel sélectionné, le processus à l'étude peut être approximé par une séquence "exponentielle" - un complexe (An) ou la somme de deux exponentielles conjuguées complexes (AR).
En tant que processus de test, une séquence de 512 échantillons avec un intervalle d'échantillonnage conditionnel Δt = 0,01 s obtenu à partir d'un processus déterministe continu (1) a été utilisée.
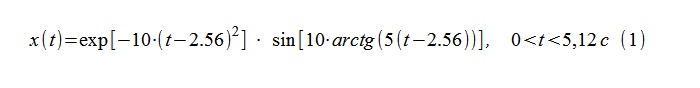
Par le «logarithme» et la différenciation subséquente du remplissage haute fréquence et de l'enveloppe, respectivement, de (1), on obtient des expressions théoriques pour la fréquence (instantanée) et la décrémentation (2)

Pour la modélisation An par la méthode du périodogramme (transformée de Fourier directe et inverse), un signal analytique y [i] est généré à partir de la séquence initiale x [i].
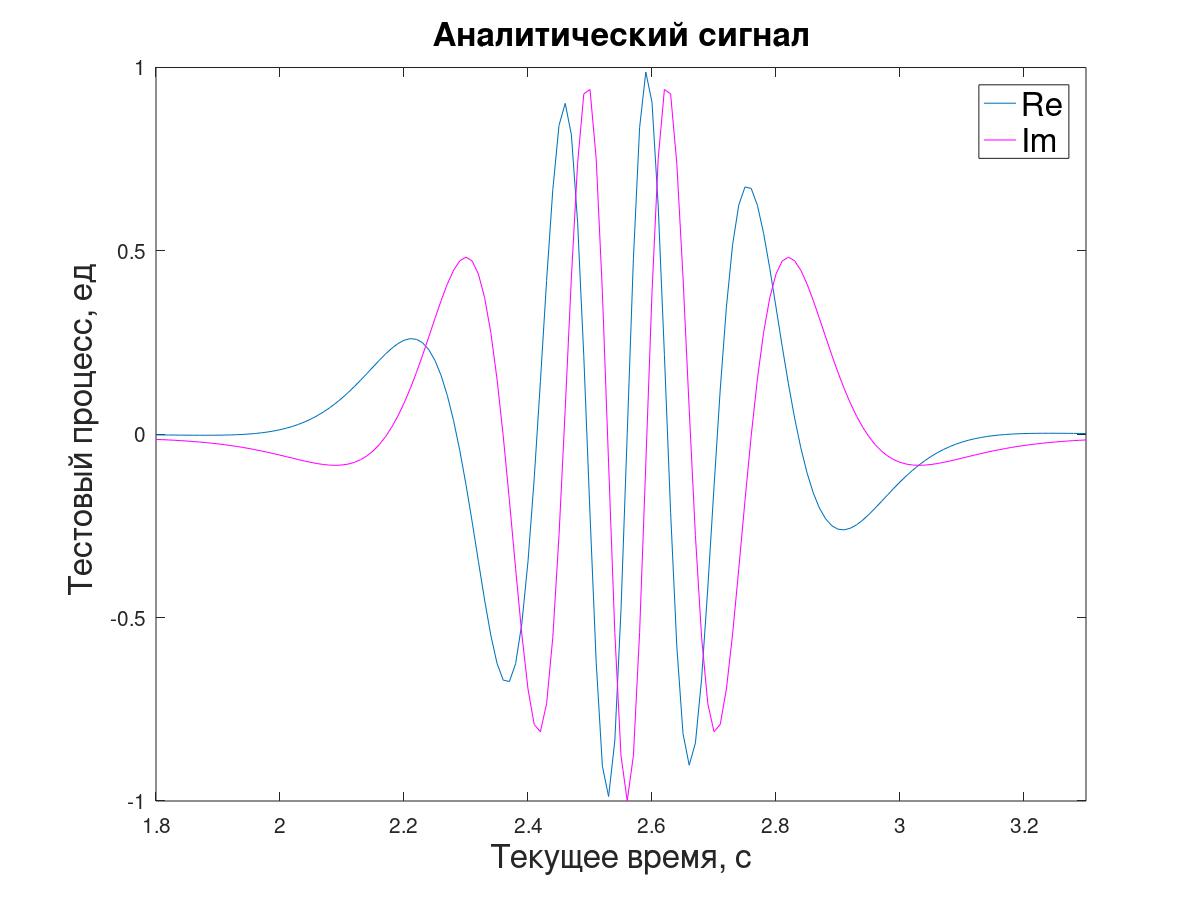
Le rapport de deux échantillons consécutifs d'un tel signal, en principe, permet de déterminer l'impédance instantanée λ, mais afin de simplifier cette tâche de démonstration - afin de ne pas se soucier de créer des échantillons intermédiaires ou d'expliquer le décalage de l'estimation par Δt / 2 - il a été décidé de travailler avec des échantillons «à travers un», en calculant λ
i par rapport aux valeurs de signal y [i + 1] suivantes par rapport à la valeur y [i-1] (3) précédente.

Pour la modélisation AR (un modèle de second ordre), la procédure standard pour calculer les coefficients d'autocorrélation 1, a
1i , a
2i en utilisant les équations de Yule-Walker a été utilisée, et les séquences à 5 échantillons x [i-2], x [i -1], ... x [i + 2] (4).
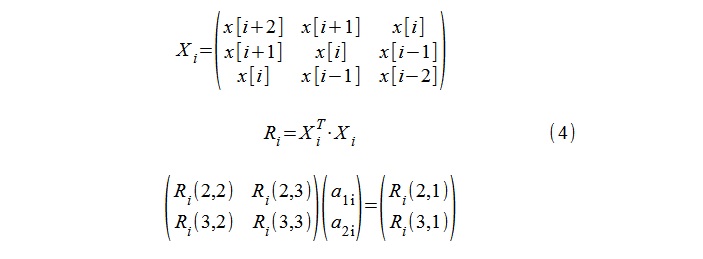
Les «pôles» du modèle λ
i sont ensuite facilement calculés par logarithme des racines de l'équation quadratique (5).
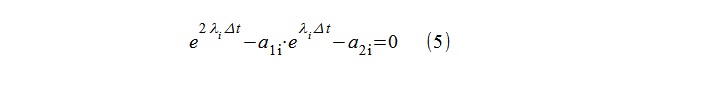

La construction d'estimations spectrales à partir de "pôles" connus jusqu'à un facteur d'échelle n'est
pas difficile . Ensuite. La «puissance instantanée» pour le modèle An est évidemment définie comme | y [i] |
2 , et la question de la mise à l'échelle de cette estimation semble être réglée. Pour le modèle AR, la technique habituelle associée à la détermination de la puissance du bruit blanc conventionnel, dans le cas d'un signal instationnaire, «ne fonctionne pas». Faute de meilleures idées, une mise à l'échelle a été appliquée sur la base du carré moyen des 5 échantillons correspondants. Il semble que rien de plus ne peut être fait en analysant uniquement la séquence de 5 échantillons. L'animation montre comment le diagramme AR SPM «échoue» parfois de manière notable par rapport au score An. Il faut comprendre que les moments de la transition «à zéro» pour le modèle AR peuvent être difficiles non seulement en termes d'erreurs à fréquence instantanée, mais aussi d'amplitude instantanée, notamment dans la région des basses fréquences.
Quelques commentaires à la fin.
- D'après l'expérience, les deux méthodes donnent généralement de bons résultats pour estimer la fréquence instantanée, au moins dans la plage de fréquence moyenne (basée sur la fréquence d'échantillonnage).
- La qualité relativement élevée des résultats de la méthode An, sa simplicité et sa facilité de compréhension et de mise en œuvre sont plus que «compensées» par les difficultés éventuelles de transformation du procédé selon Gilbert. Un filtre numérique Gilbert de bonne qualité, en particulier dans une large gamme de fréquences, peut avoir un ordre trop élevé. Lors de la mise en œuvre d'une méthode alternative de périodogramme de cette transformation, il faut tenir compte du fait que la transformée de Fourier implique implicitement l'achèvement du processus à périodique. En conséquence, un achèvement significatif significatif du processus avec des zéros peut être nécessaire. La haute qualité des résultats de la méthode An s'explique par son utilisation d'informations sur un très vaste voisinage de l'instant choisi (à proprement parler - sur l'ensemble de la mise en œuvre temporaire du processus), et cette même propriété rend difficile la mise en œuvre de la méthode (par exemple, lorsque l'on travaille en temps réel).
- Si nécessaire, les mesures suivantes peuvent être recommandées pour améliorer les résultats de la méthode AR:
- Amincissement des données (à un taux d'échantillonnage excessivement élevé)
- Une augmentation du nombre de moyennes - une extension du «moment de temps» impliqué dans le modèle du voisinage - la construction d'une matrice de piste X avec un grand nombre de lignes.
- Augmenter l'ordre du modèle AR.