En science asynchrone, la place centrale est occupée par la propriété des circuits, appelés indépendance de la vitesse, en anglais indépendant de la vitesse (ci-après SI). On pense que cette propriété est un analogue de l'indépendance des circuits asynchrones des retards des éléments logiques. Sans surprise, le terme SI est mentionné dans presque tous les travaux sur l'asynchronie. Mais périodiquement, de vagues doutes surgissent concernant ce terme. Ce n'est pas un hasard si ce terme est de plus en plus remplacé par un autre terme appelé auto-synchronisation. Un appel à la source aidera à clarifier cette situation. Nous parlons du
deuxième volume du livre de R. Miller's Theory of Switching Circuits, ou plus précisément, du chapitre 10, intitulé Theory of Switching Circuits, Independent of Speed.
Voici donc la définition des circuits indépendants de la vitesse.

Une classe (équivalence) est un ensemble complet d'états admissibles d'un circuit tel que pour tout état de cet ensemble, il existe une séquence d'états admissibles à partir d'un état donné et contenant tous les états d'un ensemble donné. En d'autres termes, à partir de n'importe quel état d'une classe, vous pouvez entrer dans n'importe quel état de la même classe.
Une classe (équivalence) est définitive s'il est impossible de passer des états d'une classe donnée à un état appartenant à une autre classe.
Par exemple, tous les modes de vie (comportements) sont indépendants de la vitesse. De plus, ils ne dépendent pas de la vitesse du circuit, qui finit nécessairement par s'arrêter, et dans un seul état.
De plus, l'auteur établit une connexion entre les schémas SI d'une part, et les schémas de distribution semi-modulaires et séquentiels d'autre part. Et en conclusion, il cite une liste de propriétés remarquables de circuits indépendants de la vitesse.

Le premier point est particulièrement intéressant. Il indique simplement que les circuits indépendants de la vitesse ne dépendent pas des retards des éléments logiques. Malheureusement, le texte n'énonce pas explicitement les motifs de cette conclusion. C'est peut-être la raison des malentendus ultérieurs concernant le terme SI. En réalité, cette conclusion est tout à fait vraie. Au début du chapitre 10, l'auteur fournit des règles de calcul des états ultérieurs.

La transition du circuit à l'état suivant est le résultat de la commutation de la sortie d'un élément logique (ou des sorties de plusieurs éléments). C'est-à-dire que l'intervalle de temps entre la création de conditions pour commuter un élément logique (excitation) et sa commutation elle-même n'est limité par rien. Et une telle période de temps est un retard de l'élément logique. Autrement dit, dès le début, l'auteur part de l'hypothèse que les retards des éléments logiques peuvent être arbitrairement importants. En effet, ce qui suit est écrit un peu plus loin.

Eh bien, pour dissiper tous les doutes, une citation de la première page du chapitre 10.

Ainsi, un fait incontestable a été établi: l'indépendance vis-à-vis des retards des éléments logiques n'est pas une propriété d'un circuit, mais une propriété du modèle dans lequel ce circuit est étudié. C'est-à-dire que tout circuit, SI ou non SI, étudié de la même manière que celle décrite par R. Miller, est indépendant des retards des éléments logiques. Dans le même temps, tout circuit peut être étudié dans un modèle avec un délai limité. Dans un tel modèle, l'ensemble des états admissibles est un sous-ensemble de l'ensemble des états admissibles lorsque l'on considère le même schéma dans un modèle avec un retard d'élément illimité. Lors de l'examen d'un circuit dans un modèle avec un retard d'élément limité, le circuit peut être indépendant de la vitesse et en même temps dépendre des retards d'élément.
Ainsi, il s'avère que l'indépendance du circuit vis-à-vis des retards des éléments logiques n'est en aucun cas liée à la propriété SI. La question se pose alors: à quoi bon introduire une définition de l'indépendance à la vitesse? En effet, considérons deux modèles et leur comportement.
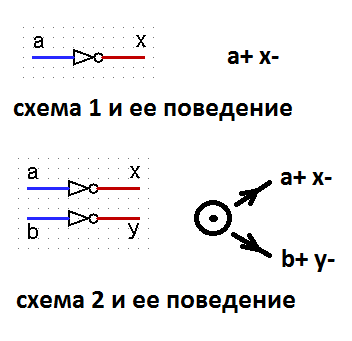
Les signaux a, b pour les deux circuits sont entrés, les signaux x, y sont sortis. Les deux schémas mettent en œuvre des comportements parfaitement raisonnables. Mais en même temps, le circuit 1 ne dépend pas de la vitesse et le circuit 2 n'a pas une telle propriété. Oui, nous pouvons dire que la définition de SI a été introduite sans diviser les signaux en entrée et en sortie. Mais une telle séparation des signaux par l'auteur était implicite, et il y a une remarque dans le texte à ce sujet.
Le sens et le caractère raisonnable de l'introduction de la définition de la propriété SI ne sont révélés qu'en relation avec la propriété de semi-modularité. Pour les circuits ayant la propriété de semi-modularité, chaque signal ne peut supprimer son excitation que par sa commutation. Les schémas non semi-modulaires lors de la mise en œuvre physique sont semés d'embûches et d'états métastables. Seuls les schémas semi-modulaires peuvent être considérés comme stables.
Mais le lien entre les propriétés de semi-modularité et l'indépendance vis-à-vis de la vitesse est unilatéral. Autrement dit, les schémas semi-modulaires sont indépendants de la vitesse, mais l'inverse n'est pas vrai. Les circuits SI peuvent ne pas être semi-modulaires. C'est-à-dire qu'une propriété vraiment importante divisant les circuits en fonction de la stabilité est la semi-modularité. Il est important de comprendre que les circuits semi-modulaires peuvent également dépendre des retards des éléments logiques, si on les considère dans un modèle à retard limité.
Mais ce n'est pas tout. La propriété de semi-modularité est également définie pour les circuits autonomes, c'est-à-dire sans diviser les signaux en entrée et en sortie. De ce fait, les schémas de libre choix (comportements) ne répondent pas aux critères de semi-modularité. Pendant ce temps, ces schémas peuvent être aussi stables que semi-modulaires. Par exemple, le schéma 2 ci-dessus n'est pas semi-modulaire, mais en termes de stabilité, il n'est en aucun cas inférieur au schéma 1, qui est semi-modulaire.
Il existe un moyen de sortir de cette impasse. Le livre J. Logic Synthesis for Asynchronous Controllers and Interfaces, J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno, A. Yakovlev, définit la propriété de la persistance de sortie (OP).

C'est la propriété OP qui est la propriété réelle qui sépare les schémas (comportements) en stable et non stable. C'est la propriété OP qui devrait remplacer la propriété SI. Il ne faut pas oublier que l'indépendance aux retards des éléments logiques est une propriété du modèle dans lequel les circuits (comportements) sont étudiés. Et les circuits OP peuvent également dépendre des retards des éléments s'ils sont pris en compte dans un modèle à retard limité.
Malgré toutes les critiques précédentes, il n'y a aucune plainte contre R. Miller. Il n'y a aucune erreur logique dans son travail. Le blâme pour plus d'un demi-siècle d'erreur réside davantage dans les lecteurs qui ont mal interprété le travail de R. Miller.
Et enfin, une conclusion agréable de ce qui précède. Le modèle comportemental STG fournit un délai illimité pour les éléments logiques. Les règles pour changer les marquages, extraire la table de vérité sont formulées à partir de l'hypothèse d'éléments de retard illimités. Par conséquent, tout circuit obtenu en calculant des fonctions logiques en utilisant STG (soit en utilisant une table de vérité soit directement en utilisant un graphe) est évidemment indépendant des retards des éléments logiques. Certes, il faut comprendre que de nouvelles manipulations avec le schéma résultant peuvent entraîner la perte de cette qualité précieuse.