Preuve trouvée que tous les changements sont un mélange d'ordre et de chance

Toutes les descriptions des changements sont un mélange unique de hasard et de déterminisme, selon la preuve radicale de «l'hypothèse faible» de Pinsker

Imaginez un jardin où poussent toutes les fleurs du monde - des orchidées délicates, des tournesols imposants, des fleurs de cire du cactus Carnegie et des inflorescences puantes de l' amorphophallus titanesque . Imaginez maintenant que toute cette diversité végétale se résume à deux options et qu'en les croisant, vous pouvez produire toutes les autres.

C'est la nature de l'une des preuves les plus radicales obtenues ces dernières années. Il a été réalisé par Tim Austin , un mathématicien de l'Université de Californie à Los Angeles. Mais au lieu des fleurs, le travail d'Austin est associé à l'un des objets les plus étudiés en mathématiques: une description mathématique des changements.

Ces descriptions, appelées systèmes dynamiques , s'appliquent à tout, des mouvements planétaires aux fluctuations des marchés boursiers. Partout où un système dynamique apparaît, les mathématiciens veulent comprendre ses principes fondamentaux. Et l'un des faits de base est que tout système dynamique arbitrairement complexe peut être divisé en éléments aléatoires et déterministes.

Cette question fait l'objet de «l'hypothèse faible» du Pinsker, qui a été formulée pour la première fois dans les années 1970. La preuve de l'hypothèse présentée par Austin fournit une méthode élégante et intuitive de penser à toutes sortes de phénomènes obscurs. Il a montré que, essentiellement, chacun de ces systèmes dynamiques est un mélange de hasard et de déterminisme.

Destin et chance

Un système dynamique commence avec certaines données d'entrée, par exemple, avec la position du pendule, applique certaines règles, par exemple, les lois du mouvement de Newton, et produit un certain résultat, par exemple, la position du pendule en une seconde. Ce qui est important, les systèmes dynamiques vous permettent de répéter ce processus: vous pouvez prendre une nouvelle position du pendule, appliquer les mêmes règles et obtenir sa position en une seconde.

Les systèmes dynamiques sont également purement mathématiques. Vous pouvez sélectionner le numéro de départ, appliquer la règle "multiplier le nombre par deux" et en obtenir un nouveau. Ce système vous permet également de saisir le nombre total dans le gestionnaire de règles et d'obtenir encore plus de nombres.

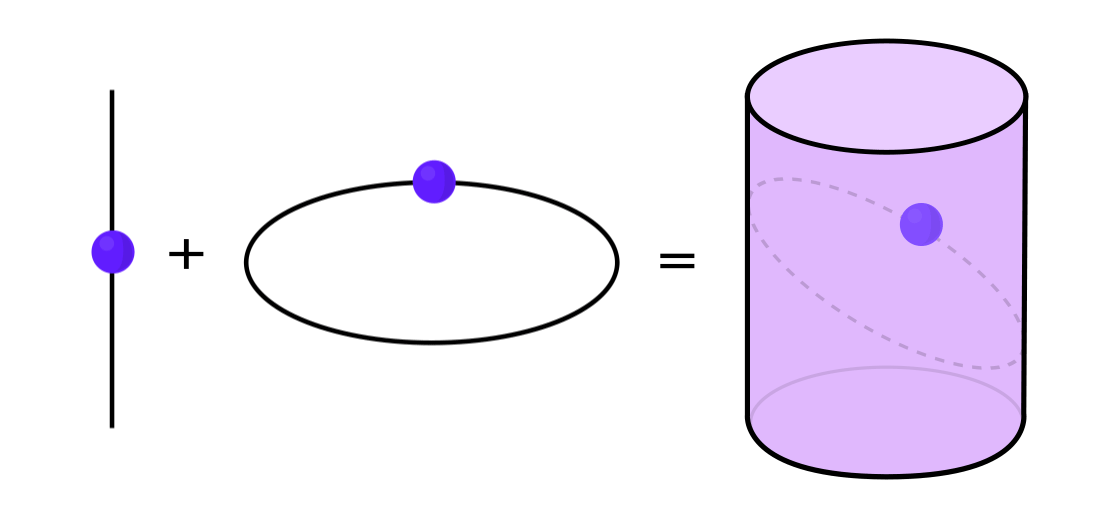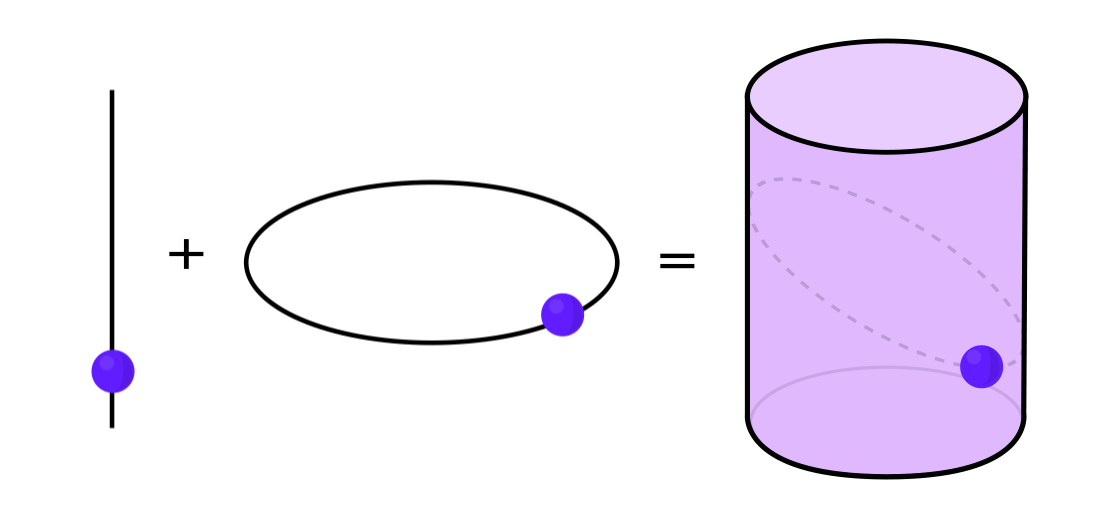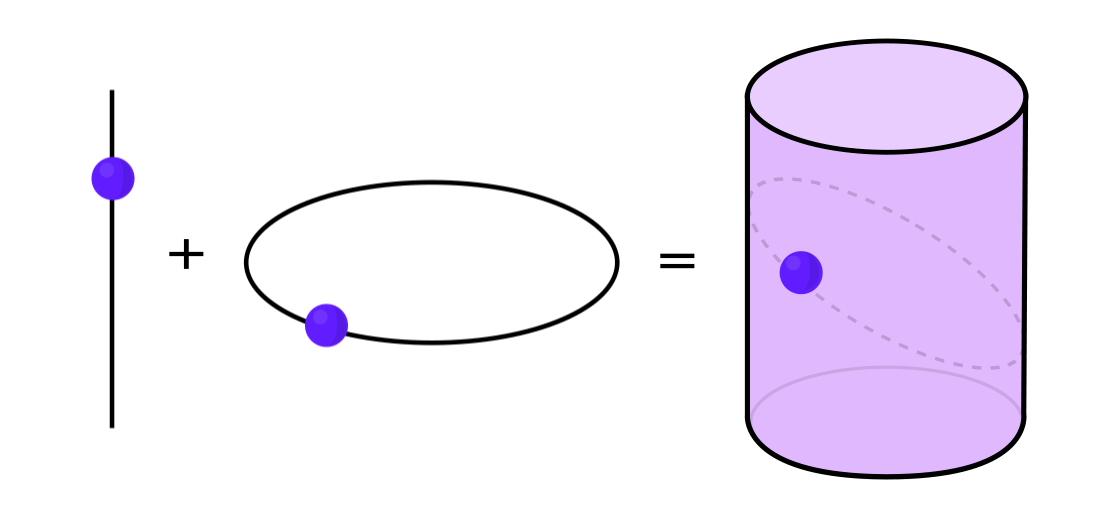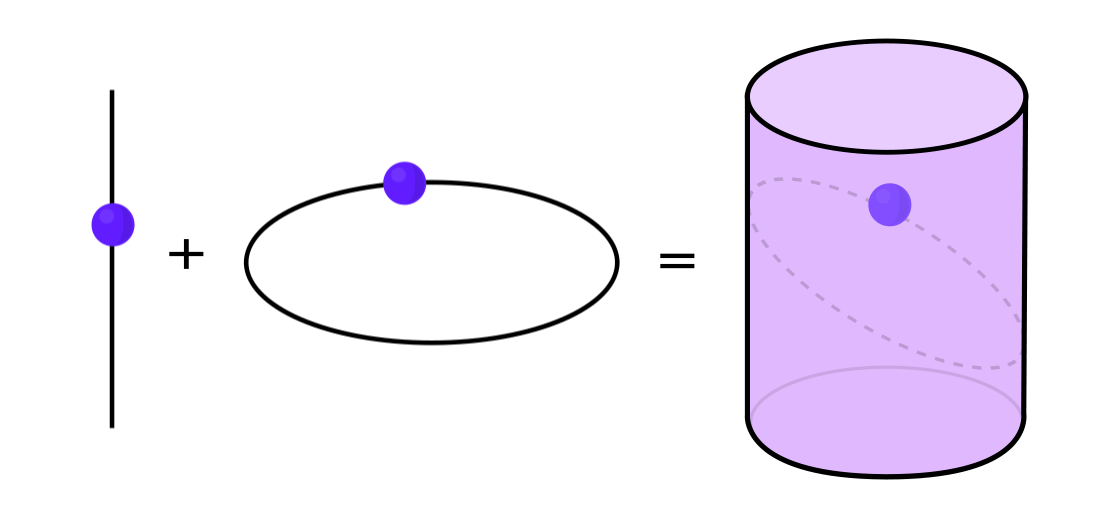
Certains types de systèmes dynamiques peuvent être exprimés comme une combinaison de deux systèmes dynamiques plus simples. Ces deux systèmes fonctionnent indépendamment l'un de l'autre, mais ils peuvent être combinés pour former un système plus complexe. Par exemple, imaginez un système dynamique déplaçant un point le long de la surface d'un cylindre. Vous entrez la position du point, appliquez les règles et obtenez un autre point.

Ce système peut être démonté en deux simples. Le premier est un système dynamique déplaçant un point autour d'un cercle. Le second est un système qui déplace un point verticalement. En combinant deux systèmes - mouvement circulaire et mouvement droit - nous obtenons un mouvement ponctuel plus complexe le long du cylindre.



«Au lieu d'étudier l'intégralité du système dynamique dans son intégralité, vous devez le diviser en parties, de petites parties qui ont du sens à étudier», a déclaré Catherine Lindsay , mathématicienne au Boston College.

Il y a deux candidats naturels pour le rôle de ces blocs de construction. Les premiers sont des systèmes dynamiques entièrement déterministes, comme notre exemple de pendule. Si vous connaissez la position du pendule à un moment donné, vous pouvez la prédire à tout moment dans le futur.


Jean-Paul Tuveno en 1975, deux ans avant la formulation de l'hypothèse faible de Pinsker

Le deuxième type de systèmes dynamiques est complètement aléatoire. Par exemple, imaginez un système dynamique avec cette règle: lancer une pièce. S'il y a un aigle, faites un pas vers la gauche; si c'est pile, c'est vrai. Le chemin final sera complètement aléatoire, c'est-à-dire que même si vous savez tout sur le chemin précédent, ces informations ne vous aideront pas à prédire la prochaine étape.

Certains systèmes dynamiques sont complètement aléatoires, d'autres sont complètement déterministes, et la plupart se situent quelque part entre les deux - ils sont un hybride des deux. Par exemple, imaginez une version légèrement modifiée de notre marche aléatoire. Nous marchons le long d'un chemin le long duquel des fleurs sont plantées, et leurs couleurs sont également aléatoires. La règle reste la même: si un aigle tombe, allez à gauche; si c'est pile, c'est vrai. Quelle sera la séquence des couleurs des fleurs?

Vous dites d'abord au hasard. Après tout, les couleurs elles-mêmes ont été choisies au hasard et votre mouvement est également aléatoire. Cependant, après avoir passé une seule fleur, la probabilité que vous la passiez à l'avenir augmente, tout simplement parce que vous n'en êtes pas loin. La séquence des couleurs des fleurs ne sera pas complètement aléatoire.

"Si vous vous tenez à côté du rouge, cela augmente les chances que vous rencontriez à nouveau le rouge en deux étapes, car il peut arriver que vous marchiez à gauche, puis à droite, et reveniez au même endroit", a déclaré Austin.

Une telle «marche aléatoire dans un paysage aléatoire» produit une sortie - une séquence de couleurs - en partie aléatoire et en partie non. En 1960, le mathématicien Mark Pinsker a suggéré qu'une certaine grande classe de systèmes dynamiques a la propriété suivante: ils sont un mélange d'un système dynamique aléatoire avec un système déterministe.

La conjecture de Pinsker est applicable à la classe des systèmes dynamiques qui ont une propriété commune importante. Les points en eux ne s'écartent pas beaucoup les uns des autres et ne rétrécissent pas au cours du développement du système. Plus précisément, si vous dessinez une boucle autour d'un ensemble de points dans votre espace (l'espace peut être quelque chose comme une surface de cylindre), commencez le développement d'un système dynamique pendant une longue période de temps, puis dessinez une boucle autour de l'ensemble de points résultant, puis la zone dans laquelle les points se trouvent fin, coïncide avec la zone qu'ils occupaient au début. De tels systèmes sont appelés «préservation des mesures»

"Si l'hypothèse originale de Pinsker était vraie, ce serait une description étonnante du monde", a déclaré Assaf Naor , mathématicien à l'Université de Princeton. Mais Pinsker avait tort. En 1973, Donald Ornstein a réfuté son hypothèse. "Le libellé était trop ambitieux", a déclaré Brina Kra , mathématicienne à la Northwestern University.

En mathématiques, il arrive souvent qu'après réfutation de l'hypothèse générale, les mathématiciens tentent d'en formuler une version plus modeste. En 1977, le mathématicien Jean-Paul Tuveno a proposé l'hypothèse faible de Pinsker. Il a adouci la formulation originale, suggérant que les systèmes dynamiques auxquels Pinsker pensait étaient le résultat de la combinaison d'un système purement aléatoire avec un système presque entièrement déterministe.

Le raffinement distingue «presque» l'hypothèse de Tuveno de l'hypothèse de Pinsker. Il voulait dire qu'un simple système déterministe devrait avoir une trace de hasard. Cette trace peut disparaître petite, mais devrait être là. Et pendant qu'il l'est, a déclaré Tuveno, l'idée de Pinsker fonctionnera.

"Il était proche de l'hypothèse d'origine, et Tuveno a montré que si tel était le cas, l'hypothèse aurait un très grand nombre d'excellentes applications", a déclaré Naor.

Au cours des décennies suivantes, les mathématiciens n'ont pas réussi à prouver l'hypothèse faible de Pinsker. L'absence de progrès a fait penser à Tuveno que même sa formulation affaiblie se révélerait fausse. "À un moment donné, j'ai pensé que tout serait le contraire, que ce ne serait pas universel", a-t-il déclaré.

Et puis Tim Austin est apparu.

Solution d'étape

Pour prouver l'hypothèse faible de Pinsker, il était nécessaire de trouver un moyen exact de passer au crible un système dynamique - celui qui lui permettrait de séparer ses parties aléatoires et presque déterministes. Des travaux antérieurs ont établi qu'il sera plus difficile d'isoler des éléments avec un peu de hasard.

"Les petits facteurs aléatoires sont beaucoup plus difficiles à attraper, et la partie centrale des preuves consiste à trouver un moyen de détecter une petite structure aléatoire", a déclaré Tuveno.


Tim Austin, mathématicien à l'Université de Californie, Los Angeles

Austin a réussi à gérer de petits éléments aléatoires d'un système dynamique en changeant les perspectives. Les systèmes dynamiques opèrent sur un espace continu, tel qu'un point se déplaçant le long de la surface d'un cylindre ou un pendule oscillant dans l'espace. Dans ces espaces, les points se déplacent le long d'arcs continus conformément aux règles d'un système dynamique. De plus, ces systèmes fonctionnent sur un nombre infini d'étapes - ils peuvent agir pour toujours.

Mais dans sa preuve, Austin a abandonné l'espace lisse continu et a oublié le travail éternel des systèmes dynamiques. Au lieu de cela, il a commencé à analyser ce qui se passerait s'ils étaient autorisés à travailler des heures discrètes, comme un million de pas. Il a ainsi appliqué la méthode inventée par Tuveno.

"La principale contribution de Tuveno a été qu'il a réalisé que si vous effectuez les étapes mathématiques correctes avec de longues lignes finies, vous pouvez prouver les propriétés d'un système dynamique", a déclaré Austin. «Ma principale contribution a été de prouver ce qui était nécessaire pour les lignes longues.»

Austin a imaginé un système dynamique émettant une séquence de uns et de zéros. Si le système dynamique lance une pièce, alors c'est facile à imaginer: les queues seront 1 et les têtes seront 0. Mais tout système dynamique peut être utilisé pour générer une séquence binaire en divisant simplement l'espace dans lequel il fonctionne en deux (pas nécessairement égaux) pièces.



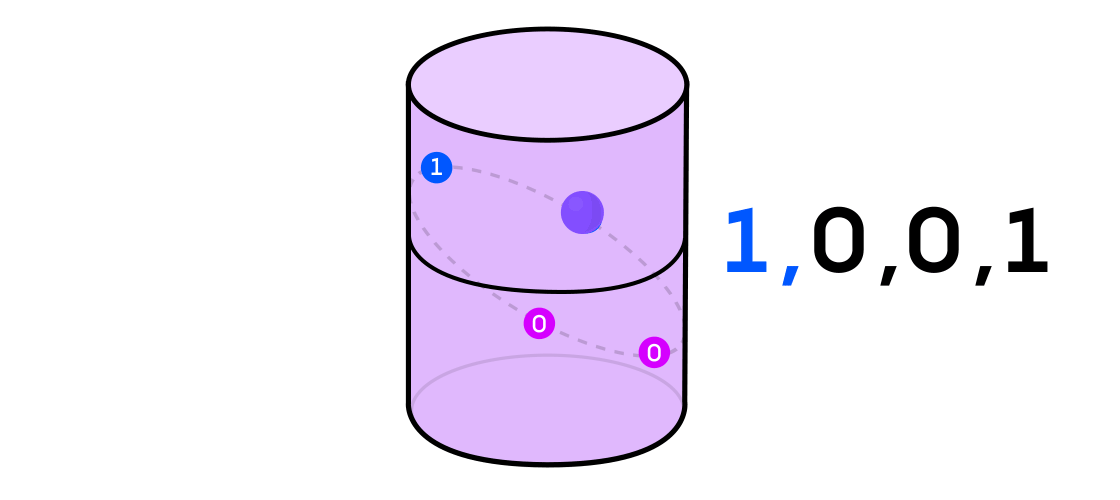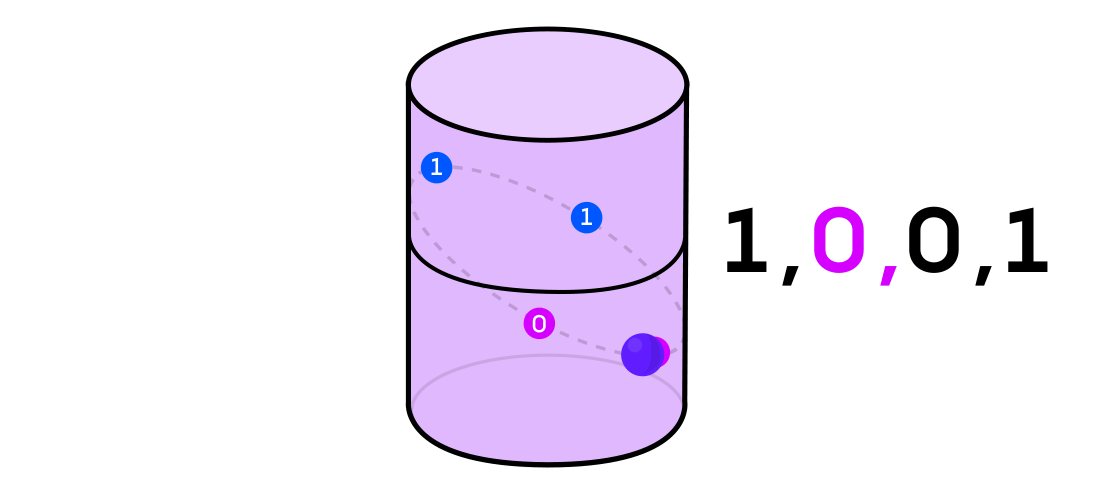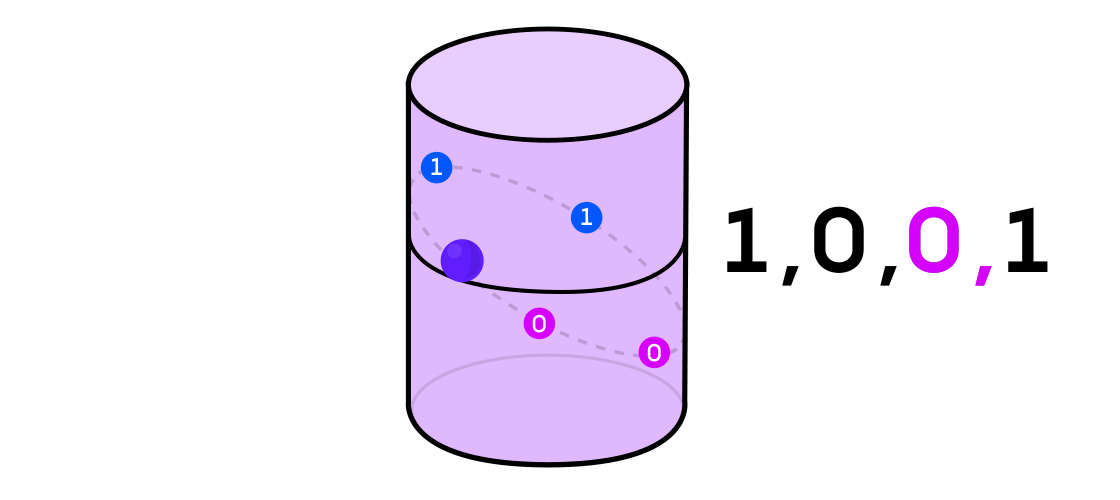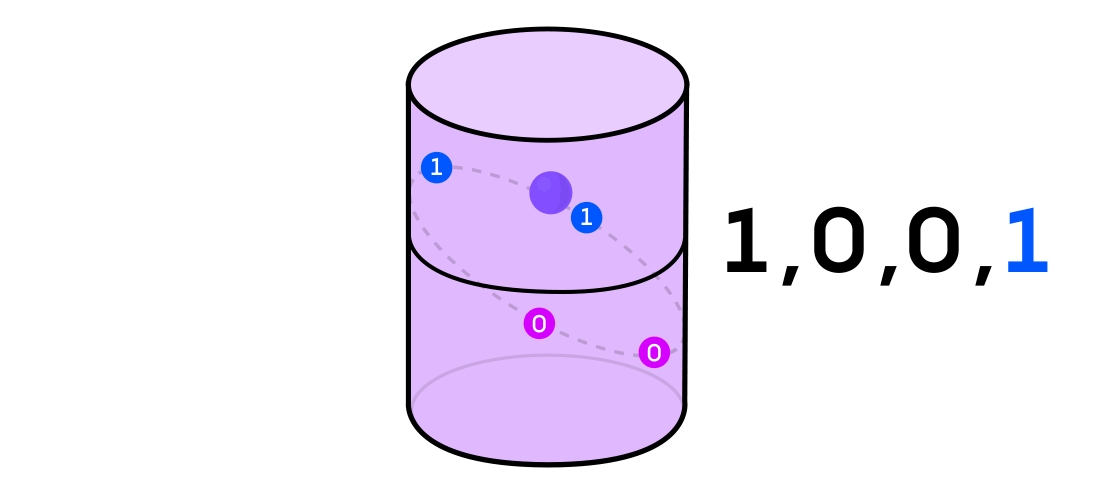
Pour revenir à l'exemple d'un système dynamique sur un cylindre, si le point se trouve sur une partie du cylindre, vous dénotez la valeur de sortie du système 1, et si de l'autre, alors 0.

Austin a analysé ces séquences binaires à l'aide d'un outil de théorie de l'information appelé Hamming Cubes . Imaginez un cube de sommets reliés par des arêtes. Des nombres binaires sont attribués à chaque sommet, disons 001 ou 101. Chaque fois, lors du passage d'un sommet à un autre, l'un des trois chiffres change.

Les cubes de Hamming peuvent être beaucoup plus compliqués que les nôtres, ils peuvent avoir autant plus d'arêtes et de sommets dans plus de trois dimensions - mais ils ont tous la propriété, en raison de la distance entre deux sommets - ou le nombre d'arêtes que vous devez parcourir passer d'un sommet à un autre est égal au nombre de places où se distinguent les lignes d'information correspondant à ces sommets. Par conséquent, 000 est situé à la distance d'un bord de 001, de deux bords de 011 et de trois de 111.



Pour isoler les éléments aléatoires et déterministes qui composent un système dynamique complexe, Austin a réfléchi à la fréquence à laquelle un système dynamique peut produire une séquence donnée de zéros et de uns représentés sur un cube de Hamming. Il a prouvé que ces séquences sont distribuées dans un cube d'une certaine manière. Ils s'accumulent dans un petit nombre de sous-régions de cubes - et ce cluster reflète le déterminisme du système - cependant, ils sont répartis au hasard parmi les séquences au sein de ces clusters, ce qui reflète le caractère aléatoire du système.

Un tel rond-point était nécessaire pour résoudre un problème qui ne cédait pas aux attaques directes.

"Ce qui m'a surpris, ce n'est pas tant la vérité ou la fausseté de l'hypothèse faible de Pinsker, mais comment cela s'est avéré, car cette tâche semblait si insidieuse", a déclaré Lewis Bowen, mathématicien à l'Université du Texas à Austin. «Avant que les preuves n'apparaissent, nous, dans l'ensemble, ne savions pas si cela pouvait être fait du tout.»

Le résultat d'Austin donne la structure de base à une large gamme de systèmes dynamiques. Pour les mathématiciens, qui tournent souvent parmi des objets qui semblent interconnectés, il n'est pas clair comment la preuve donne leur géographie exacte. Maintenant, ils ont un guide pour ces systèmes dynamiques, bien que l'on ne sache pas encore à quel type de découvertes cela conduira.

«Les mathématiciens sont toujours intéressés par les éléments constitutifs qui composent quoi que ce soit», a déclaré Lindsay. "La preuve d’Austin est un excellent résultat, qui aura probablement de nombreuses applications en mathématiques pures, mais je ne peux pas dire ce qu’elles seront."