👨🏿‍🏭 🐰 👩🏽‍🍳 Analyse des ondelettes. 3e partie 👇🏽 🦀 👩🏾‍🏫

Présentation

Lorsque vous effectuez une analyse CWT à l'aide de la bibliothèque PyWavelets (un logiciel open source gratuit publié sous la licence MIT), il y a des problèmes avec la visualisation du résultat. Le programme de test de visualisation proposé par les développeurs est présenté dans la liste suivante:

Annonce

import pywt import numpy as np import matplotlib.pyplot as plt t = np.linspace(-1, 1, 200, endpoint=False) sig = np.cos(2 * np.pi * 7 * t) + np.real(np.exp(-7*(t-0.4)**2)*np.exp(1j*2*np.pi*2*(t-0.4))) widths = np.arange(1, 31) cwtmatr, freqs = pywt.cwt(sig, widths, 'cmor1-1.5') plt.imshow(cwtmatr, extent=[-1, 1, 1, 31], cmap='PRGn', aspect='auto', vmax=abs(cwtmatr).max(), vmin=-abs(cwtmatr).max()) # doctest: +SKIP plt.show() # doctest: +SKIP

Lorsque vous travaillez avec des ondelettes complexes, par exemple avec 'cmor1-1.5', le programme génère une erreur:

 File"C:\Users\User\AppData\Local\Programs\Python\Python36\lib\site-packages\matplotlib\image.py", line 642, in set_data raise TypeError("Image data cannot be converted to float") TypeError: Image data cannot be converted to float

Cette erreur, ainsi que les difficultés à choisir l'échelle (largeurs) pour fournir la résolution de temps nécessaire, rendent difficile, en particulier pour les utilisateurs novices, d'étudier l'analyse CWT, ce qui m'a incité à écrire cet article à caractère pédagogique.

Le but de cette publication est d'envisager l'utilisation du nouveau module de visualisation de scalogrammes pour l'analyse de signaux simples et spéciaux, ainsi que lors de l'utilisation de méthodes de normalisation, de mise à l'échelle logarithmique et de synthèse, qui fournissent des informations supplémentaires dans l'analyse des séries chronologiques.

L'article utilisait des informations de la publication «Une douce introduction aux ondelettes pour l'analyse des données» . Dans les listes d'exemples données dans la publication, les erreurs sont corrigées et chaque liste de l'exemple est ramenée à sa forme finale, ce qui permet de l'utiliser sans se familiariser avec les précédentes. Pour l'analyse en ondelettes de signaux spéciaux, les données de la base de données d' échantillons PyWavelets ont été utilisées.

Un scalogramme en ondelettes est une représentation bidimensionnelle de données unidimensionnelles. Le temps est tracé sur l'axe X, et une échelle est affichée sur l'axe Y - le résultat de la transformation en ondelettes du signal correspondant à l'amplitude du signal au temps X. La valeur analytique d'un tel affichage graphique du signal est que la résolution temporelle est affichée sur l'axe Y, ce qui donne des informations supplémentaires sur les propriétés dynamiques du signal.

Ondelette - Scalogrammes de signaux simples

1. Onde cosinus avec une enveloppe gaussienne (remplacement des ondelettes. Vous pouvez étudier la dépendance de la résolution temporelle sur l'échelle):

Annonce

 from numpy import* from pylab import* import scaleogram as scg import pywt #  ,        #       'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #    1  /  ns = 1024 time =arange(ns) scales = scg.periods2scales( arange(1, 40) ) p1=10; periodic1 = cos(2*pi/p1*time) * exp(-((time-ns/2)/200)**2) fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9)); lines = ax1.plot(periodic1); ax1.set_xlim(0, len(time)) ax1.set_title("   ") fig1.tight_layout() ax2 = scg.cws(periodic1, scales=scales, figsize=(6.9,2.9)); txt = ax2.annotate("p1=%s"%p1, xy=(100, 10), bbox=dict(boxstyle="round4", fc="w")) tight_layout() print("    :", scg.get_default_wavelet(), "(", pywt.ContinuousWavelet(scg.get_default_wavelet()).family_name, ")") show()

Fonction ondelettes pour la conversion du signal: cmor1-1.5 (ondelettes Morlet complexes)

Le signal périodique apparaît désormais sous la forme d'une bande continue horizontale au point Y = p1, dont l'intensité varie en fonction de l'amplitude du signal périodique.

Il y a un certain flou dans la détection, car la bande passante n'est pas égale à zéro, cela est dû au fait que les ondelettes ne détectent pas une fréquence, mais plutôt une bande. Cet effet est associé à la largeur de bande des ondelettes.

2. Trois impulsions sont ajoutées séquentiellement avec une période croissante (pour considérer les variations périodiques à différentes échelles: analyse multi-résolution):

Annonce

 from numpy import* import pandas as pd from pylab import* import scaleogram as scg #          #       'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) pulses = zeros(ns, dtype=float32) steps = linspace(0, ns, 8) periods = [10, 20, 40] for i in range(0,3): step_mask = (time > steps[i*2+1]) & (time < steps[i*2+2]) pulses += cos(2*pi/periods[i]*time) * step_mask fig1, ax1 = subplots(1, 1, figsize=(7,3)); lines = ax1.plot(pulses); ax1.set_xlim(0, len(time)); ax1.set_title("     "); ax1.set_xlabel("Time") fig1.tight_layout() ax2 = scg.cws(pulses, scales=scales, figsize=(7,3)) for i in range(0, 3): txt = ax2.annotate("p%d=%ds"%(i+1,periods[i]), xy=(steps[i*2]+20, periods[i]), bbox=dict(boxstyle="round4", fc="w")) ax2.plot(steps[i*2+1]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5) ax2.plot(steps[i*2+2]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5) tight_layout() show()

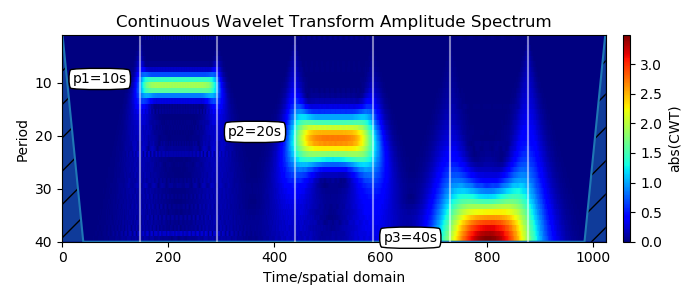
Des impulsions apparaissent à l'endroit attendu Y, correspondant à leur périodicité, elles sont localisées en fréquence et en temps. Le début de la bande et la fin correspondent à l'élan.
La bande passante évolue avec la longueur de la période. C'est une propriété bien connue de la transformée en ondelettes: lorsque l'échelle augmente, la résolution temporelle diminue. Ceci est également connu comme le compromis entre le temps et la fréquence. Lorsque vous regardez un spectrogramme de ce type, vous faites beaucoup d'analyses de résolution.

3. Trois oscillations périodiques de fréquences différentes en même temps (Wavelet - l'analyse est capable de distinguer les composantes du signal par fréquence, si leurs différences sont significatives):

Annonce

 from numpy import* import pandas as pd from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) allwaves = np.zeros(ns, dtype=np.float32) periods = [10, 20, 40] for i in range(0,3): allwaves += cos(2*np.pi/periods[i]*time) fig1, ax1 = subplots(1, 1, figsize=(6.5,2)); lines = ax1.plot(allwaves); ax1.set_title("  ") ax1.set_xlim(0, len(time)); ax1.set_xlabel("") fig1.tight_layout() ax2 = scg.cws(allwaves, scales=scales, figsize=(7,2)) tight_layout() show()

4. Un signal périodique non sinusoïdal (La différence dans les transformations en ondelettes d'un signal d'onde triangulaire avec une période de 30 secondes par rapport à celles précédemment considérées est considérée):

Annonce

 from numpy import* from pylab import* import scipy.signal import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) ptri = 30.0 # period in samples raising = 0.8 # fraction of the period raising triangle = scipy.signal.sawtooth(time/ptri*2*pi, raising) # plot the signal fig1, ax1 = subplots(1, 1, figsize=(7,3)); lines = ax1.plot(triangle); ax1.set_xlim(0, len(time)) ax1.set_title("triangle wave increasing 80% of the time with a 30s period") fig1.tight_layout() # and the scaleogram ax2 = scg.cws(triangle, scales=scales, figsize=(7,3)); txt = ax2.annotate("first harmonic", xy=(100, 30), bbox=dict(boxstyle="round4", fc="w")) txt = ax2.annotate("second harmonic", xy=(100, 15), bbox=dict(boxstyle="round4", fc="w")) tight_layout() show()

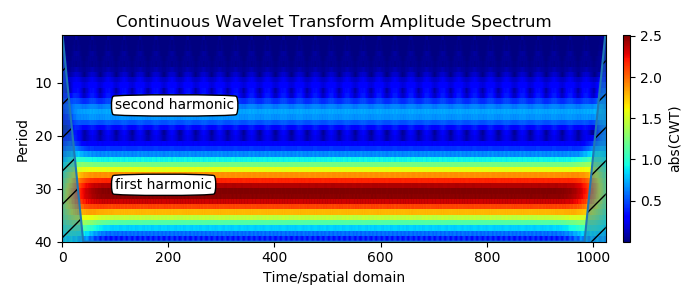
Une large bande est la première harmonique. La deuxième harmonique est visible exactement à la moitié de la valeur de la période de la première harmonique. C'est le résultat attendu pour les signaux périodiques non sinusoïdaux. Des éléments verticaux flous apparaissent autour de la deuxième harmonique, qui est plus faible et a une amplitude de 1/4 de la première pour une forme d'onde triangulaire.

5. Les impulsions lisses (gaussiennes) sont similaires aux structures de données réelles. (Cet exemple montre comment utiliser l'analyse en ondelettes pour détecter les changements de signal localisés au fil du temps):

Une série d'impulsions lisses avec différentes valeurs sigma:

$2 \ cdot \ sigma _ {1} = 2$
$2 \ cdot \ sigma _ {2} = 10$
$2 \ cdot \ sigma _ {3} = 20$

Largeur d'impulsion:

$\ omega _ {1} = 2$
$\ omega _ {2} = 20$
$\ omega _ {3} = 100$

Annonce

 from numpy import* from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) #       s1=1; s2=5; s3=10 events = [ns*0.1, ns*0.3, ns*0.7] bumps = exp(-((time-events[0])/s1)**2) + exp(-((time-events[1])/s2)**2) + \ exp(-((time-events[2])/s3)**2) #      w1=1; w2=5; w3= 50 steps = ((time > events[0]-w1) & (time < events[0]+w1)) + \ ((time > events[1]-w2) & (time < events[1]+w2)) + \ ((time > events[2]-w3) & (time < events[2]+w3)) #   fig1, (ax1, ax2) = subplots(1, 2, figsize=(11, 2)); ax1.set_title("Bumps"); ax2.set_title("Steps") lines = ax1.plot(bumps); ax1.set_xlim(0, len(time)) lines = ax2.plot(steps); ax2.set_xlim(0, len(time)) fig1.tight_layout() #   scales_bumps = scg.periods2scales(arange(1, 120, 2) ) fig2, (ax3, ax4) = subplots(1, 2, figsize=(14,3)); ax3 = scg.cws(bumps, scales=scales_bumps, ax=ax3) ax4 = scg.cws(steps, scales=scales_bumps, ax=ax4) for bmpw, stepw in [(2*s1, 2*w1), (2*s2,2*w2), (2*s3, 2*w3)]: ax3.plot(ax3.get_xlim(), bmpw*ones(2), 'w-', alpha=0.5) ax4.plot(ax4.get_xlim(), stepw*ones(2), 'w-', alpha=0.5) fig2.tight_layout() show()

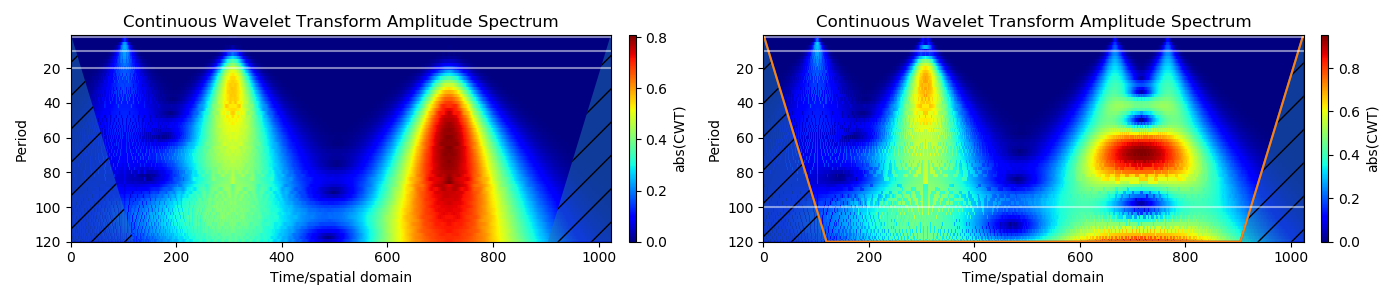
Des impulsions discrètes créent des structures coniques sur le sialogramme, également connues sous le nom de cône d'influence. Les impulsions lisses (gaussiennes) sont similaires aux structures de données réelles et créent des cônes s'étendant vers de grandes échelles. Les lignes de guidage horizontales correspondent approximativement à des périodes de temps (2 s, 10 s, 20 s). Par conséquent, l'impulsion est similaire à un signal périodique avec une période.

6. Bruit (afficher le bruit sur le sialogramme):

Annonce

 from numpy import* from pylab import* import scaleogram as scg import random scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #    1  /  ns = 1024 time =arange(ns) scales = scg.periods2scales( arange(1, 40) ) noise =random.sample(range(ns), ns) fig1, ax1 = plt.subplots(1, 1, figsize=(6.2,2)); ax1.set_title("  ") lines = ax1.plot(time, noise) ax1.set_xlim(0, ns) fig1.tight_layout() ax2 = scg.cws(noise, scales=scales, figsize=(7,2)) tight_layout() show()

Le bruit est généralement affiché sous la forme d'un ensemble d'éléments et certaines irrégularités peuvent ressembler à des objets de données réelles.Par conséquent, lorsque vous utilisez des données réelles, vous devez être prudent et, si nécessaire, vérifier le niveau de bruit. L'horaire supérieur sera différent à chaque démarrage du programme.

Formes d'onde spéciales du signal ondelette

La base de données PyWavelets contient vingt signaux spéciaux de transformée en ondelettes qui seront utiles à la fois pour l'étude et le développement. Par conséquent, je vais donner une liste qui vous permet d'effectuer une analyse en ondelettes des vingt signaux:

Annonce

 #!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from pylab import* import scaleogram as scg import pywt signals = pywt.data.demo_signal('list') signal_length=1024 for signal in signals: if signal in ['Gabor', 'sineoneoverx']: x = pywt.data.demo_signal(signal) else: x = pywt.data.demo_signal(signal, signal_length) times=[] signals=[] for time, sig in enumerate(x.real): times.append(time) signals.append(sig) scg.set_default_wavelet('cmor1-1.5') scales = scg.periods2scales( arange(1, 40) ) fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9)); lines = ax1.plot(signals); ax1.set_xlim(0, len(times)) ax1.set_title("%s"%signal) fig1.tight_layout() ax2 = scg.cws(signals, scales=scales, figsize=(6.9,2.9)); tight_layout() show()

Je ne donnerai qu'un seul résultat de la transformée en ondelettes du signal Doppler:

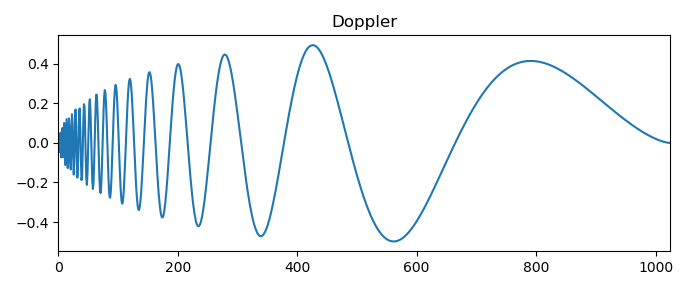
Les variétés les plus courantes de signaux simples et spéciaux sont considérées, ce qui nous permet de passer à l'utilisation d'un scalogramme pour résoudre certains problèmes d'analyse de séries chronologiques.

Scalogrammes de chronologie d'ondelettes

1. Données de fécondité des CDC aux États-Unis 1969-2008 (les données de fécondité contiennent des caractéristiques périodiques, à la fois sur une échelle annuelle et sur une échelle plus petite):

Annonce

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) fig = figure(figsize=(12,2)) lines = plot(births.index, births.values/1000, '-') xlim(datetime_lim) ylabel("Nb of birthes [k]"); title("Total births per day in the US (CDC)"); xlim = xlim() ax = scg.cws(births, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day") set_x_yearly(ax, len(births)) show()

Une ligne horizontale apparaît avec une fréquence d'environ 7 jours. Des valeurs élevées apparaissent près des bordures de l'échelle, ce qui est le comportement normal du traitement en ondelettes. Ces effets sont bien connus comme un cône d'influence, c'est pourquoi un masque (facultatif) recouvre cette zone.

2. Normalisation (la suppression de la valeur moyenne - births_normed = births-births.mean () est obligatoire, sinon les limites des données sont considérées comme des étapes qui créent beaucoup de fausses détections en forme de cône):

Annonce

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() ax = scg.cws(births_normed, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day") set_x_yearly(ax, len(births)) show()

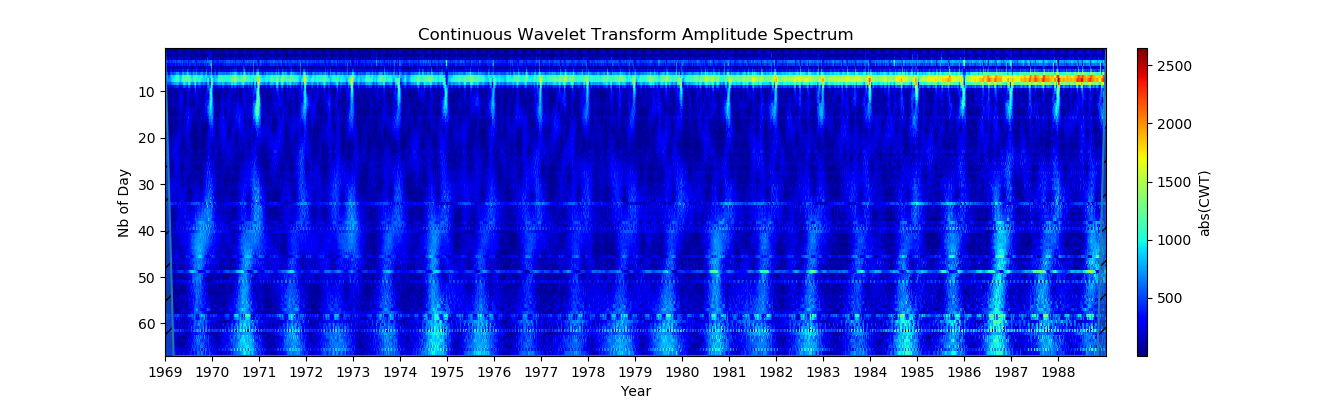
3. Changement d'échelle d'amplitude (pour voir les objets annuels, en utilisant period2scales () l' échelle le long de l'axe Y est spécifiée).

Annonce

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() scales = scg.periods2scales(np.arange(1, 365+100, 3)) ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 5), xlabel="Year", ylabel="Nb of Day", clim=(0, 2500)) set_x_yearly(ax, len(births)) show()

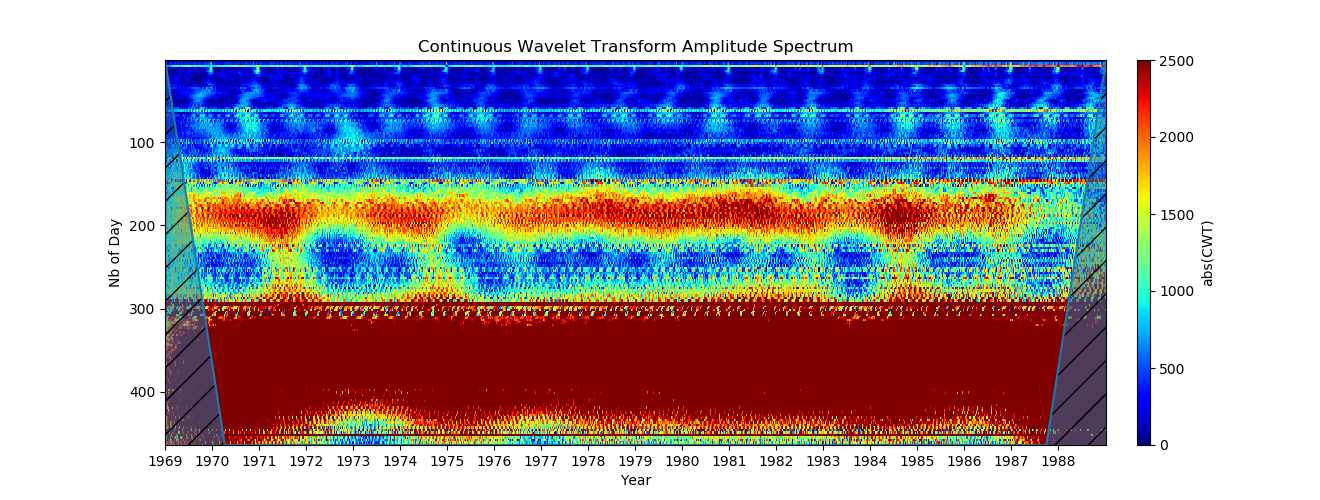
La plage d'amplitude de la carte des couleurs (axe Y) est désormais définie par clim = (0,2500). La valeur exacte de l'amplitude d'oscillation dépend de l'ondelette, mais restera proche de l'ordre de la valeur réelle. C'est bien mieux, maintenant on voit très bien la variation annuelle, ainsi qu'environ 6 mois!

4. Utilisation de l'échelle logarithmique (Afin de pouvoir voir des périodes petites et grandes en même temps, il est préférable d'utiliser l'échelle logarithmique sur l'axe Y. Ceci est réalisé en utilisant l'option xscale = log.)

Annonce

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() scales = scg.periods2scales(np.arange(1, 365+100, 3)) ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) print("Number of available days:", len(births_normed)) show()

Le résultat est bien meilleur, mais maintenant les pixels à de faibles valeurs de périodes sont allongés le long de l'axe Y.

5. Distribution uniforme sur une échelle logarithmique (Pour obtenir une distribution uniforme sur une échelle, les valeurs de période doivent être uniformément réparties puis converties en valeurs d'échelle, comme indiqué ci-dessous :):

Annonce

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #  CWT  ,       cwt = scg.CWT(births_normed, scales=scales) ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) bboxf = dict(boxstyle="round", facecolor="y", edgecolor="0.5") arrowpropsf = dict(facecolor='yellow', shrink=0.05) text = ax.annotate("unusual\nfeature", xy=(365*6, 15), xytext=(365*3, 50), bbox=bboxf, arrowprops=arrowpropsf) show()

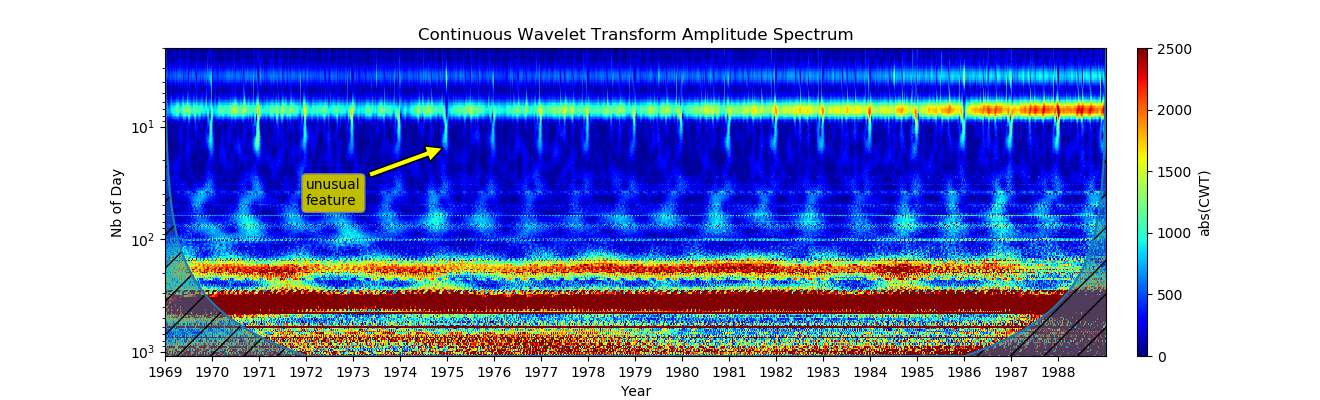
Nous pouvons voir des changements de signal à toutes les échelles. Le sialogramme montre chaque année en périodes égales.

6. Mise en évidence d'une partie de la chronologie (vérification des données intermédiaires entre les marques de chronologie à la recherche d'artefacts ou de données manquantes.):

Annonce

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) #    : 1974-1976 fig = figure(figsize=(12,4)) lines =plot(births.index, births.values/1000, '-') xlim(pd.to_datetime("1974-01-01"), pd.to_datetime("1976-01-01")) ylabel("Nb of birthes [k]"); title("Total births per day bw 1974 and 1976"); #      ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) xlim = ax.set_xlim( (1974-1969)*365, (1976-1969)*365 ) show()

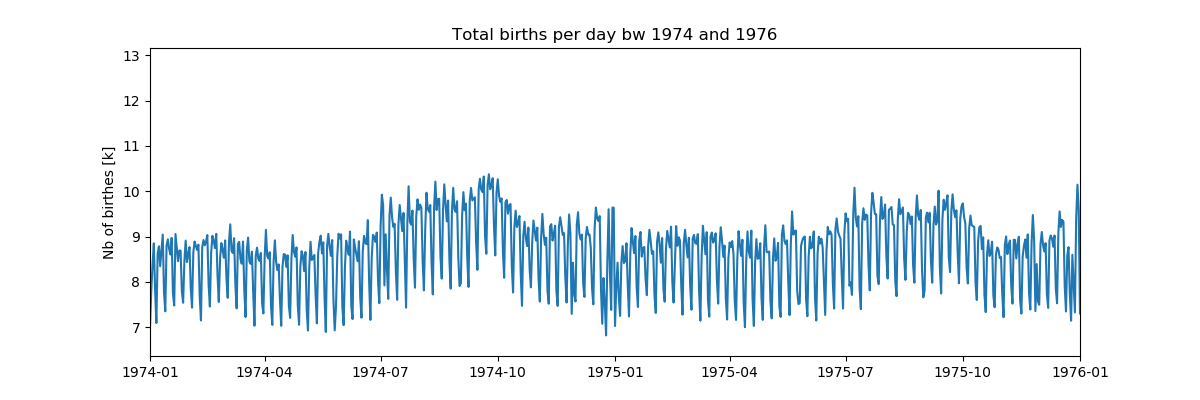
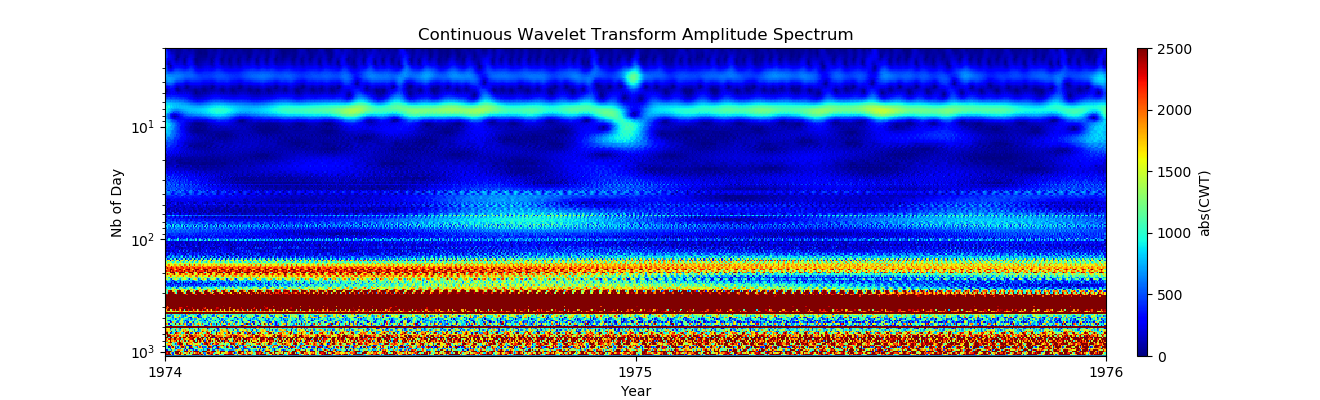À première vue, les modèles hebdomadaires semblent très uniformes, mais quelque chose se passe le jour de Noël, regardons à nouveau cette période:

Annonce

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) # :  1975    1976  fig = figure(figsize=(12,4)) lines = plot(births.index, births.values/1000, '.-') xlim(pd.to_datetime("1974-12-01"), pd.to_datetime("1975-02-01")) ylabel("Nb of birthes [k]"); title("Total births per day : 2 monthes zoom"); #      ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) xlim = ax.set_xlim( (1975-1969)*365-30, (1975-1969)*365+30 ) show()

Maintenant, il est clair que c'est l'effet de la fin de l'année:

Noël: le 23/24/25 décembre montre un nombre anormalement bas de naissances, et ces jours s'écartent de l'horaire hebdomadaire;
Il existe des données pour décembre, ce qui est cohérent avec la présence d'une certaine valeur pour les dates concernées les 1er et 2 janvier, ces dates sont généralement inférieures aux événements personnels

7. Synthèse (un sialogramme est construit à partir de données normalisées, avec une meilleure lisibilité pour toutes les échelles):

Annonce

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) bbox = dict(boxstyle="round", facecolor="w", edgecolor="0.5") bbox2 = dict(boxstyle="round", facecolor="y", edgecolor="0.5") arrowprops = dict(facecolor='white', shrink=0.05) arrowprops2 = dict(facecolor='yellow', shrink=0.05) for period, label in [ (3.5, "half a week"), (7, "one week"), (365/2, "half a year"), (365, "one year"), (365*2.8, "long trends")]: text = ax.annotate(label, xy=(365*5.5, period), xytext=(365*2, period), bbox=bbox, arrowprops=arrowprops) text = ax.annotate("end of year\neffect", xy=(365*6, 15), xytext=(365*3, 50), bbox=bbox2, arrowprops=arrowprops2) text = ax.annotate("increase in\nvariations *amplitude*", xy=(365*18.5, 7), xytext=(365*14, 50), bbox=bbox2, arrowprops=arrowprops2) show()

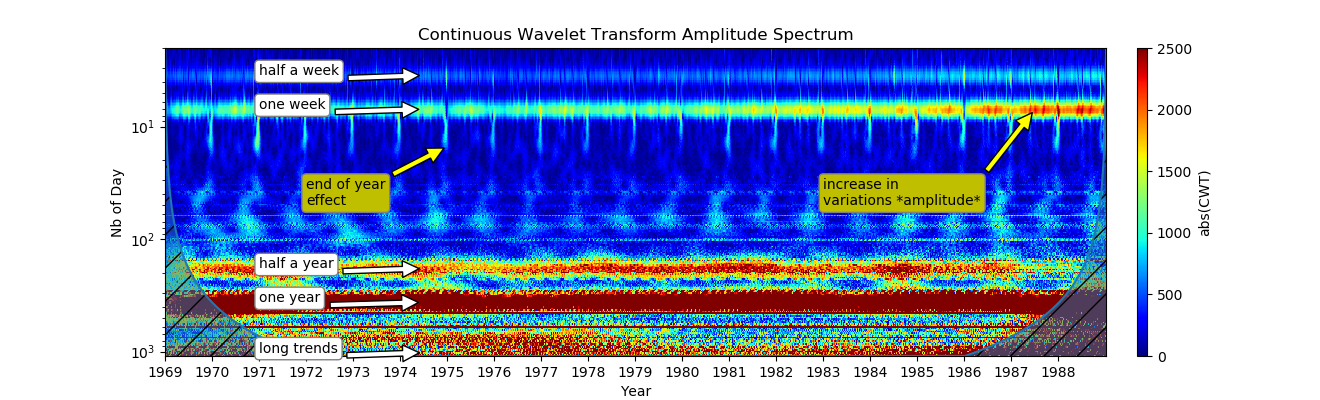CWT révèle beaucoup d'informations en peu de temps:

une variation hebdomadaire montrant les habitudes hospitalières est présente depuis plusieurs décennies;

Dans les années 80, l'indicateur hebdomadaire a augmenté, ce qui peut être dû à un changement des habitudes de travail des hôpitaux, à un changement de la fécondité ou à un simple changement de population;

La deuxième bande semestrielle est clairement la deuxième harmonique. Des motifs flous apparaissent dans la zone de 3 à 1 mois, ce qui peut être dû à la troisième harmonique, car les fluctuations annuelles sont si fortes. Elle peut également être causée par l'effet des vacances sur la fertilité et peut nécessiter un complément d'étude;

L'effet de fin d'année a été constaté à Noël et au 1er janvier. Celui-ci peut être resté invisible avec une autre méthode de fréquence.

Conclusions:

Dans cette publication, nous avons vu comment la forme de base des variations de signal se traduit par un scalogramme. Un exemple d'ensemble de données ordonné dans le temps a ensuite été utilisé pour montrer étape par étape comment CWT est appliqué aux données standard.

La technique ci-dessus peut être étendue pour analyser le trafic réseau et détecter le comportement inhabituel des objets. CWT est un outil puissant qui est de plus en plus utilisé comme entrée pour les réseaux de neurones et peut être utilisé pour créer de nouvelles fonctions pour classer ou détecter les anomalies.

Chaque exemple est implémenté comme un programme indépendant, ce qui vous permet de choisir un exemple pour votre tâche, sans plonger dans les exemples précédents et suivants. L'utilisateur peut essayer n'importe quelle fonction ondelette de la liste donnée au début de chaque programme, par exemple, mexh ou gaus5. Par exemple 1, respectivement:

PS Pour l'utilisation pratique des listes, je donnerai les versions des modules utilisés:

 >>> import scaleogram; print(scaleogram .__version__) 0.9.5 >>> import pandas; print(pandas .__version__) 0.24.1 >>> import numpy; print(numpy .__version__) 1.16.1 >>> import matplotlib; print(matplotlib .__version__) 3.0.2

Pour un ensemble indépendant de données dans le fichier * .csv, j'apporte la structure des données (dans une colonne):
année, mois, jour, sexe, naissances
1969,1,1, F, 4046
1969,1,1, M, 4440
1969,1,2 , F, 4454
1969.1.2, M, 4548
...
Pour les pandas de la version 0.24.1, vous devrez enregistrer explicitement les convertisseurs matplotlib.

Pour enregistrer des convertisseurs:

 from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()

Analyse des ondelettes. 3e partie

Présentation

Ondelette - Scalogrammes de signaux simples

Formes d'onde spéciales du signal ondelette

Scalogrammes de chronologie d'ondelettes

Conclusions:

More articles: