ARA: algorithme pour trouver le nombre maximum de points sur une ligne droite

Récemment, je suis tombé sur une tâche classique pour les entretiens: rechercher le nombre maximum de points se tenant sur une ligne droite (sur un plan, coordonnées entières). L'idée d'une recherche exhaustive m'est immédiatement venue à l'esprit, qui a une complexité temporelle évidente en O (n ^ 2), mais il me semblait qu'il devrait y avoir autre chose, au moins une alternative en O (n * log (n)) . Après une demi-heure, même quelque chose de mieux a été trouvé!



_{Une description plus détaillée du problème avec des exemples d'entrée-sortie se trouve sur GeeksForGeeks et LeetCode}

Au début, j'ai remarqué que vous pouvez facilement résoudre le problème uniquement pour les lignes horizontales ou verticales, en ajoutant le X / Y de chaque point dans le dictionnaire. Et quelle est la différence entre les autres lignes? Juste une pente? .. Mais c'est réparable!

J'ai donc décidé qu'il était possible de faire le tour de toute la liste de points plusieurs fois en les faisant pivoter. Et la solution dans O (n) est obtenue! Bien qu'avec un grand coefficient. J'espère vraiment que je n'ai pas inventé un vélo :)

# ***  *** #   #    = 180/ROT_COUNT  # #      12, #  180*4    (6% ), #  180*20   (0% ). # ó    . #     - . ROT_COUNT = 180*10 #  #        , #       1 / MULT_COEF. #    4  . #   MULT_COEF   ROT_COUNT. # ó    - . #     - . MULT_COEF = 2 ** 3 angles = list(map(lambda x: x*180.0/ROT_COUNT, range(ROT_COUNT))) def mnp_rotated(points, angle): """Returns Maximum Number of Points on the same line with given rotation""" #   rad = math.radians(angle) co = math.cos(rad) si = math.sin(rad) #      counts = {} for pair in points: #    nx = pair[0]*co - pair[1]*si #       , #      #       #      nx = int(nx * MULT_COEF) #   if nx in counts: counts[nx] += 1 else: counts[nx] = 1 #    return max(counts.values()) def mnp(points): """Returns Maximum Number of Points on the same line""" res = 0 best_angle = 0 #      for i in angles: current = mnp_rotated(points, i) #  ,     if current > res: res = current best_angle = i return res 

Visualisé, il ressemble à ceci:
_{mon premier GIF fait maison, ne gronde pas :)}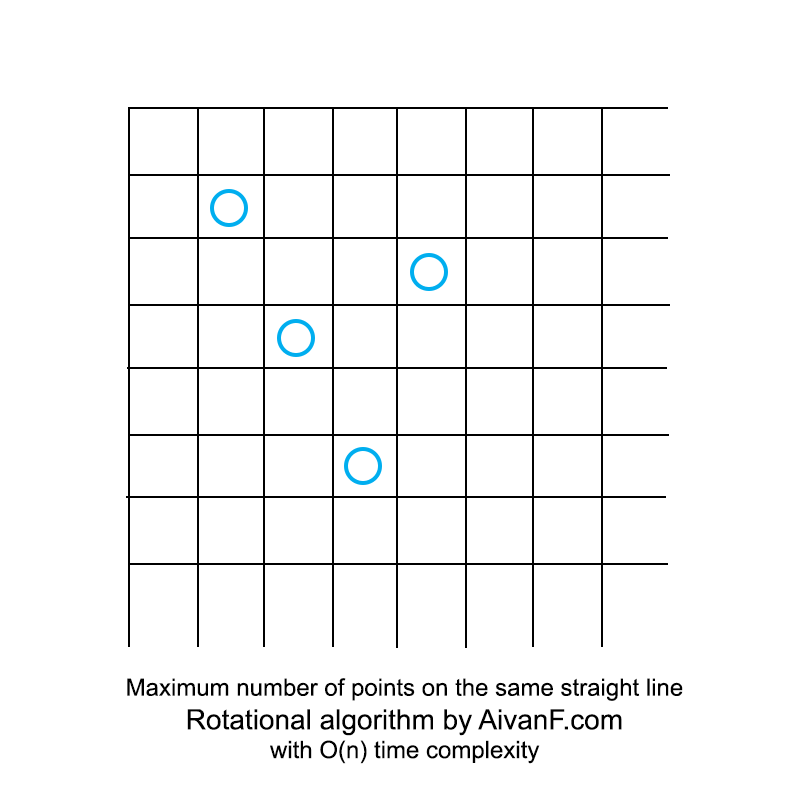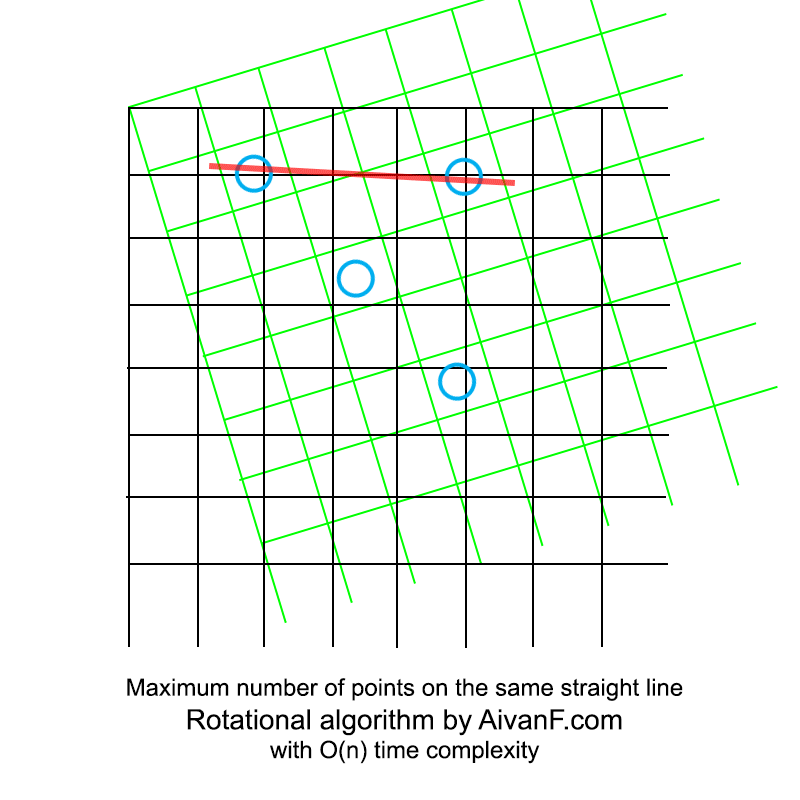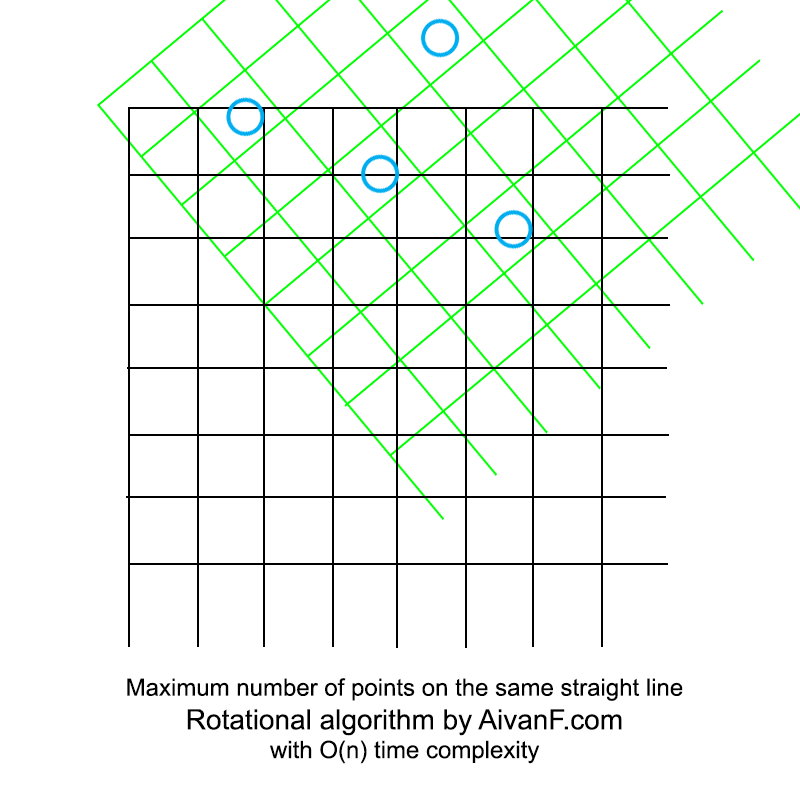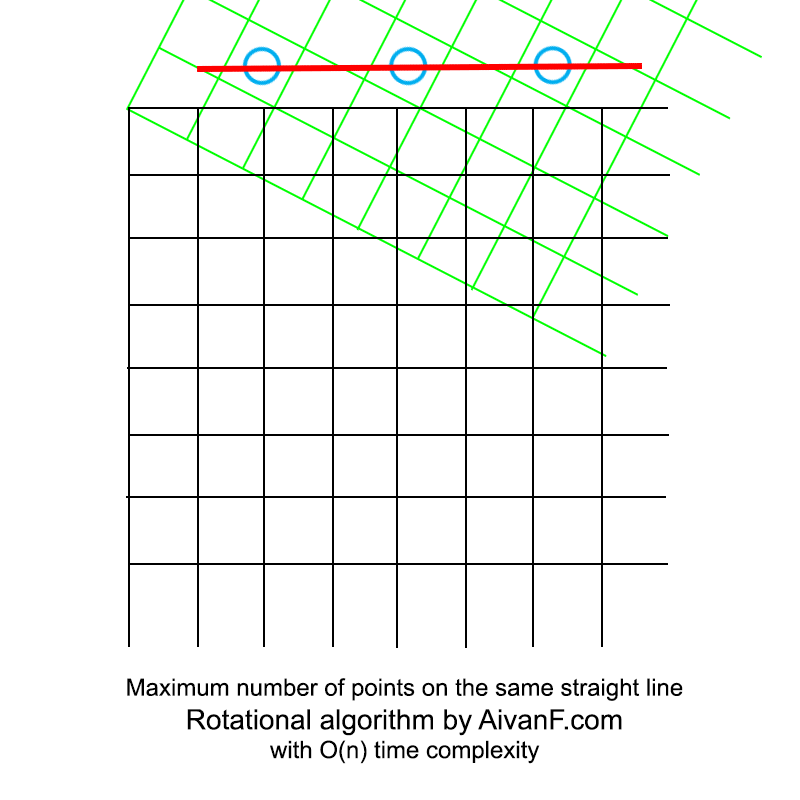



Il est intéressant de noter que la mise en œuvre ultérieure de la recherche exhaustive a pris plus de lignes de code.

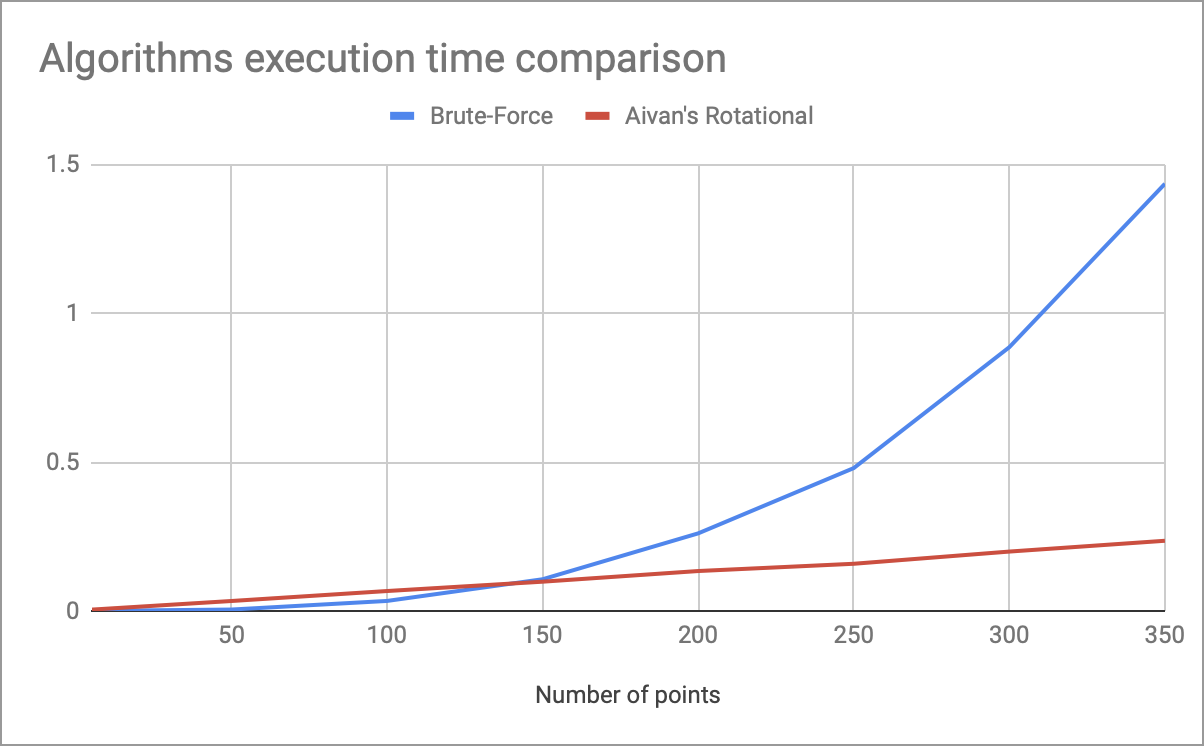
Le graphique avec les mesures de l'exécution de mon algorithme de rotation et l'énumération complète en fonction du nombre de points se trouve dans l'en-tête.


Environ 150 points montrent l'avantage de la complexité linéaire dans le temps (avec les coefficients utilisés dans le code ci-dessus). Par conséquent, cet algorithme présente les inconvénients suivants:

• La précision n'est pas absolue.
• Le temps d'exécution sur de petits ensembles de points est long.
  _{En général, cela est facilement corrigé par une sélection compétente de coefficients: pour les ensembles simples, ROT_COUNT = 36 plutôt que 2000 est assez suffisant, ce qui accélère le code 50+ fois.}

Et de tels avantages:

• Il fonctionne calmement avec des coordonnées fractionnaires.
• La complexité temporelle est linéaire, ce qui est visible sur les grands ensembles de données.

Un tableau des mesures est disponible ici . Le code source entier du projet avec les deux algorithmes et divers contrôles est sur le GitHub .

Mettre à jour Je veux encore une fois noter que cet algorithme a à la fois des avantages et des inconvénients, je ne le préconise pas comme un remplacement idéal pour la force brute, je viens de décrire une alternative intéressante intéressante, qui dans certains cas peut être plus appropriée.