
Comment faire un solveur nonogram pour Python, réécrivez-le dans Rust pour l'exécuter directement dans le navigateur via WebAssembly.
TL; DR
Commencer
À propos des mots croisés japonais (nonogrammes) sur le Habré, il y avait déjà plusieurs messages. Exemple
et un de plus .
Les images sont cryptées avec des numéros situés à gauche des lignes, ainsi qu'au-dessus des colonnes. Le nombre de nombres indique le nombre de groupes de cellules noires (ou leur couleur, pour les mots croisés de couleur) dans la ligne ou la colonne correspondante, et les nombres eux-mêmes - combien de cellules fusionnées chacun de ces groupes contient (par exemple, un ensemble de trois nombres - 4, 1 et 3 signifie que dans cette ligne, il y a trois groupes: le premier - à partir de quatre, le second - à partir d'un, le troisième - à partir de trois cellules noires). Dans un puzzle de mots croisés en noir et blanc, les groupes doivent être séparés par au moins une cellule vide, en couleur, cette règle ne s'applique qu'aux groupes monochromes, et les groupes multicolores peuvent être étroitement espacés (les cellules vides peuvent également se trouver le long des bords des lignes). Il est nécessaire de déterminer l'emplacement des groupes de cellules.
L'un des points de vue les plus généralement acceptés est que les mots croisés «corrects» ne peuvent être appelés que ceux qui sont résolus de manière «logique». Ceci est généralement appelé la méthode de solution, dans laquelle les dépendances entre différentes lignes et / ou colonnes ne sont pas prises en compte. En d'autres termes, une solution est une séquence de décisions indépendantes de lignes ou de colonnes individuelles jusqu'à ce que toutes les cellules soient remplies (en savoir plus sur l'algorithme ci-dessous). Par exemple, seuls de tels nonogrammes peuvent être trouvés sur le site Web http://nonograms.org/ ( http://nonograms.ru/ ). Les nonogrammes de ce site ont déjà été cités en exemple dans l'article Résoudre les mots croisés de couleur japonaise à la vitesse de la lumière . À des fins de comparaison et de vérification, mon solveur a également ajouté un support pour le téléchargement et l'analyse des mots croisés à partir de ce site (merci à KyberPrizrak pour la permission d'utiliser les matériaux de son site).
Cependant, le concept de nonogrammes peut être étendu à un problème plus général, lorsque la méthode "logique" habituelle conduit à une impasse. Dans de tels cas, il faut faire une hypothèse sur la couleur d'une cellule et, après avoir prouvé que cette couleur conduit à une contradiction, marquer la couleur opposée pour cette cellule. La séquence de ces étapes peut (si vous avez la patience) nous donner toutes les solutions. Cet article portera principalement sur la résolution d'un cas plus général de mots croisés.
Python
Il y a environ un an et demi, je suis tombé accidentellement sur un article qui décrivait une méthode pour résoudre une seule ligne (comme il s'est avéré plus tard, la méthode était plutôt lente).
Lorsque j'ai implémenté cette méthode en Python (mon principal langage de travail) et ajouté une mise à jour séquentielle de toutes les lignes, j'ai vu que tout cela n'était pas résolu très rapidement. Après avoir étudié le matériel, il s'est avéré que sur ce sujet, il existe de nombreux travaux et implémentations qui proposent différentes approches pour cette tâche.
Il m'a semblé que le travail le plus ambitieux sur l'analyse de diverses implémentations de solveurs a été effectué par Jan Wolter, publiant sur son site (qui, à ma connaissance, reste le plus grand référentiel public de nonogrammes sur Internet), une étude détaillée contenant une multitude d'informations et de liens qui peuvent aider à créer votre propre solveur.
En étudiant de nombreuses sources (elles seront à la fin de l'article), j'ai progressivement amélioré la vitesse et la fonctionnalité de mon solveur. En conséquence, j'étais accro et j'étais engagé dans la mise en œuvre, la refactorisation, le débogage d'algorithmes pendant environ 10 mois dans un temps libre du travail.
Algorithmes de base
Le solveur résultant peut être représenté sous la forme de quatre niveaux de décision:
( ligne ) solveur linéaire: en entrée, une ligne de cellules et une ligne de description (indices), en sortie, une ligne partiellement résolue. Dans la solution python, j'ai implémenté 4 algorithmes différents (3 d'entre eux sont adaptés aux mots croisés couleur). Le plus rapide s'est avéré être l'algorithme BguSolver, nommé d'après la source d'origine . Il s'agit d'une méthode très efficace et pratiquement standard pour résoudre des chaînes de nonogrammes en utilisant la programmation dynamique. Le pseudocode de cette méthode se trouve, par exemple, dans cet article .
( propagation ) nous mettons toutes les lignes et colonnes dans une file d'attente, nous les parcourons avec un solveur linéaire, lorsque nous recevons de nouvelles informations lors de la résolution d'une ligne (colonne), nous mettons à jour la file d'attente, respectivement, avec de nouvelles colonnes (lignes). Continuez jusqu'à ce que la ligne soit vide.
Exemple et codeNous prenons la tâche suivante à résoudre à partir de la file d'attente. Soit une chaîne vide (non résolue) de longueur 7 (nous la désignons comme ??????? ) avec une description des blocs [2, 3] . Le solveur linéaire produira une chaîne partiellement résolue ?X??XX? où X est la cellule remplie. Lors de la mise à jour de la ligne, nous voyons que les colonnes avec les numéros 1, 4, 5 ont changé (l'indexation commence à 0). Cela signifie que de nouvelles informations sont apparues dans les colonnes indiquées et peuvent être renvoyées au solveur «linéaire». Nous mettons ces colonnes dans la file d'attente des tâches avec une priorité plus élevée (afin de les donner ensuite au solveur linéaire).
def propagation(board): line_jobs = PriorityDict() for row_index in range(board.height): new_job = (False, row_index) line_jobs[new_job] = 0 for column_index in range(board.width): new_job = (True, column_index) line_jobs[new_job] = 0 for (is_column, index), priority in line_jobs.sorted_iter(): new_jobs = solve_and_update(board, index, is_column) for new_job in new_jobs:
( sondage ) pour chaque cellule non résolue, nous trions toutes les options de couleur et essayons la propagation avec ces nouvelles informations. Si nous obtenons une contradiction, nous jetons cette couleur hors des options de couleur pour la cellule et essayons d'en profiter à nouveau en utilisant la propagation. S'il est résolu jusqu'au bout, nous ajoutons la solution à la liste des solutions, mais continuons d'expérimenter avec d'autres couleurs (il peut y avoir plusieurs solutions). Si nous arrivons à une situation où il est impossible de résoudre davantage, nous ignorons simplement et répétons la procédure avec une couleur / cellule différente.
CodeRenvoie True si une contradiction est reçue à la suite de l'échantillon.
def probe(self, cell_state): board = self.board pos, assumption = cell_state.position, cell_state.color
( retour arrière ) si pendant le sondage vous n'ignorez pas un puzzle partiellement résolu, mais continuez à invoquer récursivement la même procédure, nous obtenons un retour arrière (en d'autres termes, une marche complète dans la profondeur de l'arbre de décision potentiel). Ici, un grand rôle commence à jouer, laquelle des cellules sera choisie comme la prochaine extension de la solution potentielle. De bonnes recherches sur ce sujet figurent dans cette publication .
CodeLe retour arrière est assez compliqué avec moi, mais ces deux fonctions décrivent approximativement ce qui se passe lors d'une recherche récursive
def search(self, search_directions, path=()): """ Return False if the given path is a dead end (no solutions can be found) """ board = self.board depth = len(path) save = board.make_snapshot() try: while search_directions: state = search_directions.popleft() assumption, pos = state.color, state.position cell_colors = board.cell_colors(pos) if assumption not in cell_colors: LOG.warning("The assumption '%s' is already expired. " "Possible colors for %s are %s", assumption, pos, cell_colors) continue if len(cell_colors) == 1: LOG.warning('Only one color for cell %r left: %s. Solve it unconditionally', pos, assumption) try: self._solve_without_search() except NonogramError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The path %s is invalid", assumption, pos, path) return False if board.is_solved_full: self._add_solution() LOG.warning( "The only color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True continue rate = board.solution_rate guess_save = board.make_snapshot() try: LOG.warning('Trying state: %s (depth=%d, rate=%.4f, previous=%s)', state, depth, rate, path) success = self._try_state(state, path) finally: board.restore(guess_save) if not success: try: LOG.warning( "Unset the color %s for cell '%s'. Solve it unconditionally", assumption, pos) board.unset_color(state) self._solve_without_search() except ValueError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The whole branch (depth=%d) is invalid. ", assumption, pos, depth) return False if board.is_solved_full: self._add_solution() LOG.warning( "The negation of color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True finally:
Ainsi, nous commençons à résoudre notre puzzle de mots croisés à partir du deuxième niveau (le premier ne convient que pour le cas dégénéré, alors que dans le puzzle de mots croisés entier, il n'y a qu'une seule ligne ou colonne) et montons progressivement les niveaux. Comme vous pouvez le deviner, chaque niveau provoque le niveau sous-jacent plusieurs fois, donc pour une solution efficace, il est impératif d'avoir des premier et deuxième niveaux rapides, qui peuvent être appelés des millions de fois pour des puzzles complexes.
À ce stade, il s'avère (plutôt attendu) que python n'est pas du tout l'outil qui convient aux performances maximales dans une telle tâche gourmande en CPU: tous les calculs y sont extrêmement inefficaces par rapport aux langages de bas niveau. Par exemple, le solveur BGU le plus proche algorithmiquement (en Java), selon les résultats des mesures, s'est avéré 7 à 17 (parfois jusqu'à 27) fois plus rapide sur une variété de tâches.
Plus de détails pynogram_my BGU_my speedup
Danseur 0,976 0,141 6,921986
Cat 1.064 0.110 9.672727
Skid 1.084 0.101 10.732673
Bucks 1.116 0.118 9.457627
Bord 1,208 0,094 12,851064
Fumée 1,464 0,120 12.200000
Nœud 1,332 0,140 9,514286
Balançoire 1,784 0,138 12,927536
Maman 2.108 0.147 14.340136
DiCap 2.076 0.176 11.795455
Tragic 2,368 0,265 8,935849
Merka 2.084 0.196 10.632653
Petro 2,948 0,219 13,461187
M&M 3,588 0,375 9,568000
Signé 4.068 0.242 16.809917
Léger 3,848 0,488 7,885246
Forever 111.000 13.570 8.179808
Centre 5,700 0,327 17,431193
Chaud 3.150 0.278 11.330935
Karaté 2.500 0.219 11.415525
9-Dom 510.000 70.416 7.242672
Drapeau 149.000 5.628 26.474769
Lion 71,000 2,895 24,525043
Marley 12.108 4.405 2.748695
Chose 321.000 46.166 6.953169
Nature inf 433.138 inf
Sierp inf inf NaN
Gettys inf inf NaN
Les mesures ont été effectuées sur ma voiture, les puzzles sont tirés de l'ensemble standard que Jan Wolter a utilisé dans sa comparaison
Et c'est déjà après avoir commencé à utiliser PyPy, et sur CPython standard, le temps de calcul était plus long que sur PyPy 4-5 fois! Nous pouvons dire que les performances d'un solveur Java similaire étaient 28 à 85 fois supérieures à celles du code CPython.
Les tentatives pour améliorer les performances de mon solveur à l'aide du profilage (cProfile, SnakeViz, line_profiler) ont conduit à une certaine accélération, mais bien sûr, elles n'ont pas donné un résultat étrange.
+ le solveur peut résoudre tous les puzzles des sites https://webpbn.com , http://nonograms.org et son propre format (basé sur l'ini)
+ résout les nonogrammes en noir et blanc et en couleur avec n'importe quel nombre de couleurs (le nombre maximum de couleurs rencontrées est de 10)
+ résout des puzzles avec des tailles de blocs manquantes (blott). Un exemple d'un tel puzzle .
+ peut restituer des puzzles à la console / aux curses / fenêtre du navigateur (lors de l'installation de l'option pynogram-web supplémentaire). Pour tous les modes, la visualisation de la progression de la solution en temps réel est prise en charge.
- calculs lents (par rapport aux implémentations décrites dans l'article-comparaison des solveurs, voir tableau ).
- retour arrière inefficace: certains casse-tête peuvent être résolus pendant des heures (lorsque l'arbre de décision est très grand).
Rouille
Au début de l'année, j'ai commencé à étudier Rust. J'ai commencé, comme d'habitude, avec The Book , j'ai découvert WASM, j'ai suivi le tutoriel proposé . Cependant, je voulais une tâche réelle dans laquelle vous pouvez vous impliquer dans les points forts du langage (principalement sa super-performance), et non des exemples inventés par quelqu'un. Je suis donc retourné aux nonogrammes. Mais maintenant, j'avais déjà une version de travail de tous les algorithmes en Python, il ne restait plus qu'à "réécrire".
La bonne nouvelle m'attendait depuis le tout début: il s'est avéré que Rust, avec son système de type, décrit parfaitement les structures de données pour ma tâche. Par exemple, l'une des correspondances de base BinaryColor + BinaryBlock / MultiColor + ColoredBlock vous permet de séparer de façon permanente les nonogrammes noir et blanc et couleur. Si, quelque part dans le code, nous essayons de résoudre une chaîne colorée à l'aide de blocs de description binaires ordinaires, nous obtenons une erreur de compilation sur la non-concordance de type.
Les types de base ressemblent à ceci pub trait Color { fn blank() -> Self; fn is_solved(&self) -> bool; fn solution_rate(&self) -> f64; fn is_updated_with(&self, new: &Self) -> Result<bool, String>; fn variants(&self) -> Vec<Self>; fn as_color_id(&self) -> Option<ColorId>; fn from_color_ids(ids: &[ColorId]) -> Self; } pub trait Block { type Color: Color; fn from_str_and_color(s: &str, color: Option<ColorId>) -> Self { let size = s.parse::<usize>().expect("Non-integer block size given"); Self::from_size_and_color(size, color) } fn from_size_and_color(size: usize, color: Option<ColorId>) -> Self; fn size(&self) -> usize; fn color(&self) -> Self::Color; } #[derive(Debug, PartialEq, Eq, Hash, Clone)] pub struct Description<T: Block> where T: Block, { pub vec: Vec<T>, }
Lors du portage du code, certains points ont clairement indiqué qu'un langage typé statiquement tel que Rust (enfin, ou, par exemple, C ++) est plus approprié pour cette tâche. Plus précisément, les génériques et les traits décrivent un domaine mieux que les hiérarchies de classes. Donc, dans le code Python, j'avais deux classes pour un BguSolver linéaire, BguSolver et BguColoredSolver qui résolvaient respectivement une ligne en noir et blanc et une ligne en couleur. Dans le code Rust, j'ai toujours la seule struct DynamicSolver<B: Block, S = <B as Block>::Color> générique struct DynamicSolver<B: Block, S = <B as Block>::Color> , qui peut résoudre les deux types de tâches, selon le type passé lors de la création ( DynamicSolver<BinaryBlock>, DynamicSolver<ColoredBlock> ). Bien sûr, cela ne signifie pas que quelque chose de similaire ne peut pas être fait en Python, juste dans Rust, le système de type m'a clairement indiqué que si vous n'alliez pas de cette façon, vous auriez à écrire une tonne de code répétitif.
De plus, quiconque a essayé d'écrire dans Rust, a sans aucun doute remarqué l'effet de la «confiance» dans le compilateur, lorsque le processus d'écriture du code se résume à l'algorithme pseudo-méta suivant:
write_initial_code
while (compiler_hints = $ (cargo check))! = 0; faire
fix_errors (compiler_hints)
fin
Lorsque le compilateur cesse d'émettre des erreurs et des avertissements, votre code sera cohérent avec le système de type et le vérificateur d'emprunt et vous préviendrez à l'avance l'occurrence d'un tas de bogues potentiels (bien sûr, sous réserve d'une conception soignée des types de données).
Je vais donner quelques exemples de fonctions qui montrent à quel point le code Rust peut être concis (par rapport aux équivalents Python).
unsolved_neighboursDonne une liste de "voisins" non résolus pour un point donné (x, y)
def unsolved_neighbours(self, position): for pos in self.neighbours(position): if not self.is_cell_solved(*pos): yield pos
fn unsolved_neighbours(&self, point: &Point) -> impl Iterator<Item = Point> + '_ { self.neighbours(&point) .into_iter() .filter(move |n| !self.cell(n).is_solved()) }
partial_sumsPour un ensemble de blocs décrivant une ligne, donnez des sommes partielles (en tenant compte des espaces requis entre les blocs). Les indices résultants indiqueront la position minimale à laquelle le bloc peut se terminer (cette information sera utilisée plus tard pour un solveur linéaire).
Par exemple, pour un tel ensemble de blocs [2, 3, 1] nous avons à la sortie [2, 6, 8] , ce qui signifie que le premier bloc peut être déplacé au maximum vers la gauche afin que son bord droit occupe la 2e cellule, de même pour le reste blocs:
1 2 3 4 5 6 7 8 9
_ _ _ _ _ _ _ _ _ _
2 3 1 | _ | _ | _ | _ | _ | _ | _ | _ | _ |
^ ^ ^
| | |
fin d'un bloc | | |
fin du bloc 2 -------- |
fin du bloc 3 ------------
@expand_generator def partial_sums(blocks): if not blocks: return sum_so_far = blocks[0] yield sum_so_far for block in blocks[1:]: sum_so_far += block + 1 yield sum_so_far
fn partial_sums(desc: &[Self]) -> Vec<usize> { desc.iter() .scan(None, |prev, block| { let current = if let Some(ref prev_size) = prev { prev_size + block.0 + 1 } else { block.0 }; *prev = Some(current); *prev }) .collect() }
Lors du portage, j'ai apporté plusieurs modifications
Des outils utiles
- clippy est un analyseur statique standard qui peut même parfois donner des conseils augmentant légèrement les performances du code.
- valgrind est un outil d'analyse dynamique des applications. Je l'ai utilisé comme profileur pour rechercher des botneks (
valrgind --tool=callgrind ) et en particulier des sections de code valrgind --tool=massif ( valrgind --tool=massif ). Astuce: définissez [profile.release] debug = true sur Cargo.toml avant de démarrer le profileur. Cela laissera des caractères de débogage dans l'exécutable. - kcachegrind pour afficher les fichiers de callgrind. Un outil très utile pour trouver les endroits les plus problématiques en termes de performances.
Performances
C'est pour ça que la réécriture sur Rust a commencé. Nous prenons les mots croisés du tableau de comparaison déjà mentionné et les exécutons à travers les meilleurs solveurs décrits dans l'article d'origine. Résultats et description des runs ici . Nous prenons le fichier résultant et construisons quelques graphiques dessus. Comme le temps de résolution varie de quelques millisecondes à des dizaines de minutes, le graphique est fait avec une échelle logarithmique.
courir dans un ordinateur portable jupyter import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline
solveur python
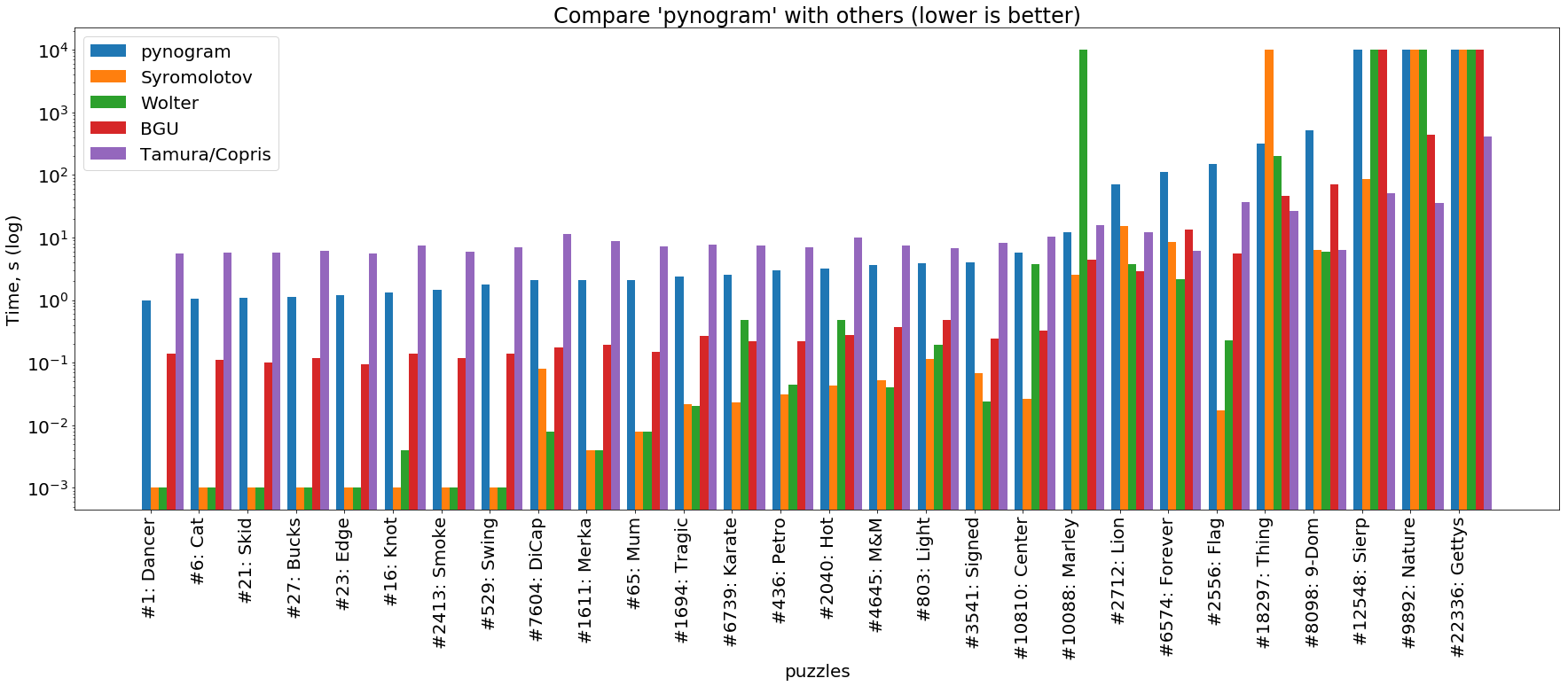
(l' image est cliquable )
Nous voyons que le pynogramme ici est plus lent que tous les solveurs présentés. La seule exception à cette règle est le solveur Tamura / Copris basé sur SAT, qui résout les puzzles les plus simples (la partie gauche du graphique) plus longtemps que le nôtre. Cependant, c'est une caractéristique des solveurs SAT: ils sont conçus pour des mots croisés super complexes dans lesquels un solveur régulier est coincé dans le retour arrière pendant une longue période. Ceci est clairement visible sur le côté droit du graphique, où Tamura / Copris résout les puzzles les plus difficiles des dizaines et des centaines de fois plus rapidement que tout le monde.
solveur de rouille
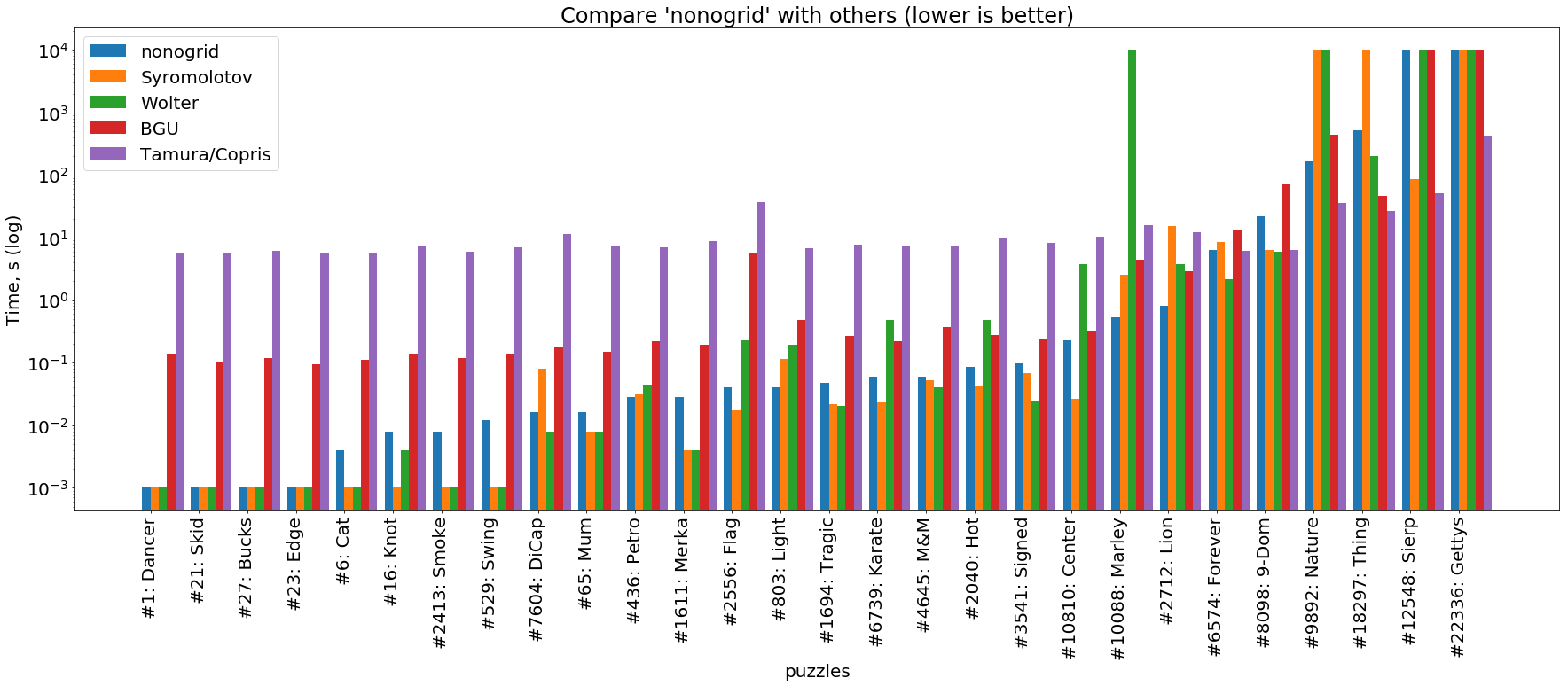
(l' image est cliquable )
Ce graphique montre que les non - grids sur des tâches simples supportent également ou légèrement pire que les solveurs hautes performances écrits en C et C ++ ( Wolter et Syromolotov ). Avec la complication des tâches, notre solveur répète approximativement la trajectoire du solveur BGU (Java), mais presque toujours devant lui d'environ un ordre de grandeur. Sur les tâches les plus difficiles, Tamura / Copris est toujours en avance sur tout le monde.
rouille vs python
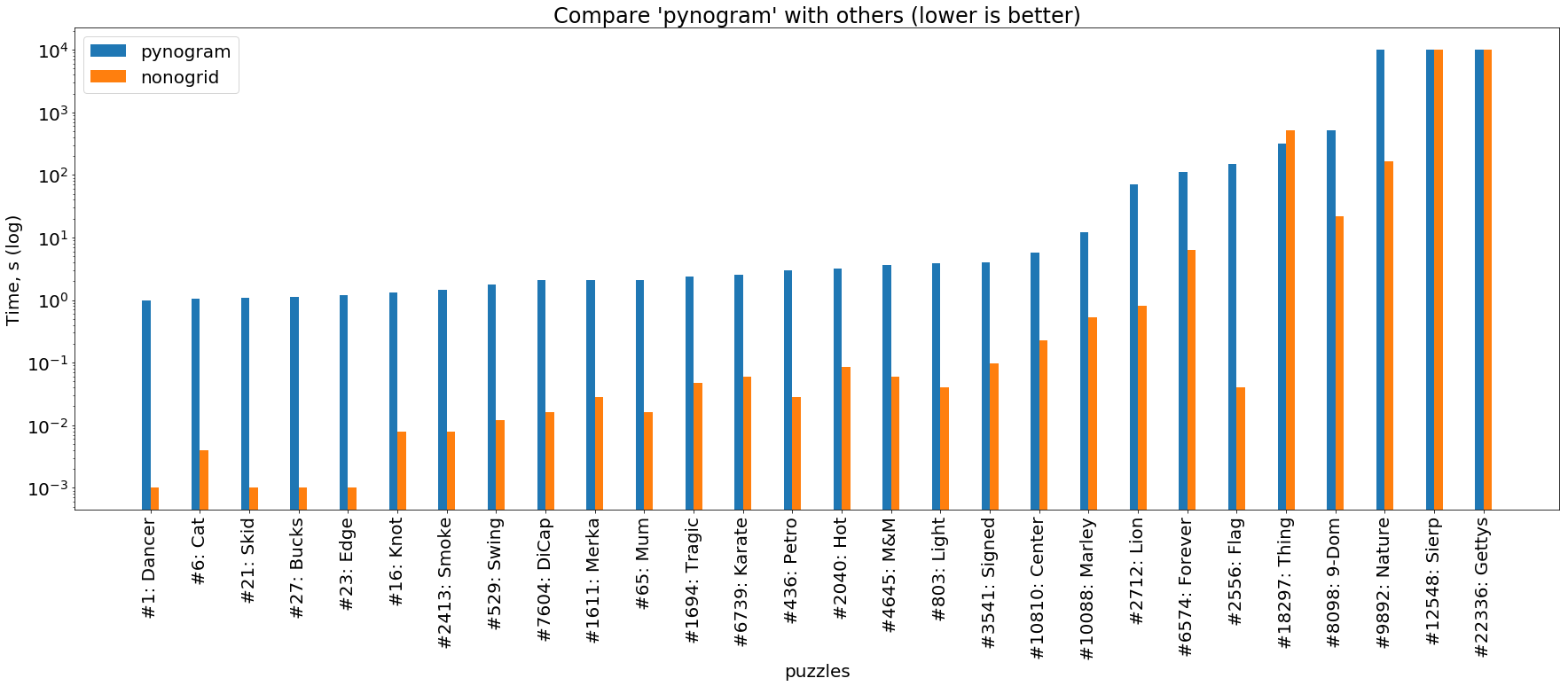
(l' image est cliquable )
Et enfin, une comparaison de nos deux solveurs décrits ici. On peut voir que le solveur Rust est presque toujours à 1 à 3 ordres de grandeur devant le solveur Python.
+ le solveur peut résoudre tous les puzzles des sites https://webpbn.com (sauf buvard - avec des tailles de bloc partiellement masquées), http://nonograms.org et son propre format (basé sur TOML)
+ résout les nonogrammes noir et blanc et couleur avec n'importe quel nombre de couleurs
+ peut rendre des puzzles sur la console (la couleur c webpbn.com dessine la vraie couleur)
+ fonctionne rapidement (en comparaison avec les implémentations décrites dans l'article-comparaison des solveurs, voir tableau).
- le retour en arrière est resté inefficace, comme dans la solution Python: certains casse-tête (par exemple , un tel 20x20 inoffensif ) peuvent être résolus pendant des heures (lorsque l'arbre de décision est très grand). Peut-être qu'au lieu de revenir en arrière, vous devriez utiliser les solveurs SAT déjà mentionnés sur le concentrateur . Certes, le seul solveur SAT que j'ai trouvé sur Rust à première vue semble inachevé et abandonné.
Webassembly
La réécriture du code dans Rust a donc porté ses fruits: le solveur est devenu beaucoup plus rapide. Cependant, Rust nous offre une autre fonctionnalité incroyablement cool: la compilation dans WebAssembly et la possibilité d'exécuter votre code directement dans le navigateur.
Pour implémenter cette fonctionnalité, il existe un outil spécial pour Rust qui fournit les liants nécessaires et génère un passe-partout pour que vous puissiez exécuter sans douleur les fonctions Rust en code JS - ce wasm-pack (+ wasm-bindgen ). La plupart du travail avec celui-ci et d'autres outils importants est déjà décrit dans le didacticiel Rust et WebAssembly . Cependant, il y a quelques points que j'ai dû comprendre par moi-même:
lors de la lecture, cela donne l'impression que le tutoriel est principalement écrit pour un développeur JS qui souhaite accélérer son code avec Rust. Eh bien, ou du moins pour quelqu'un qui connaît bien npm . Pour moi, en tant que personne loin du front-end, il était surprenant de constater que même l'exemple standard du livre ne voulait pas fonctionner avec un serveur Web tiers différent de npm run start .
Heureusement, wasm-pack dispose d'un mode qui vous permet de générer du code JS standard (qui n'est pas un module npm). wasm-pack build --target no-modules --no-typescript ne donnera que deux fichiers dans la sortie: project-name.wasm - le binaire du code Rust compilé dans WebAssembly et project-name.js . Le dernier fichier peut être ajouté à n'importe quelle page HTML <script src="project-name.js"></script> et utiliser les fonctions WASM sans se soucier de npm, webpack, ES6, des modules et autres joies du développeur JS moderne. Le mode no-modules est idéal pour les développeurs non frontaux lors du développement d'une application WASM, ainsi que pour les exemples et les démos, car il ne nécessite aucune infrastructure frontale supplémentaire.
WebAssembly convient aux tâches trop lourdes pour JavaScript. Tout d'abord, ce sont des tâches qui effectuent de nombreux calculs. Et si c'est le cas, une telle tâche peut être effectuée pendant longtemps même avec WebAssembly et ainsi violer le principe asynchrone du web moderne. Je parle de toutes sortes d' avertissement: script ne répondant pas que j'ai observé lorsque mon solveur fonctionnait. Pour résoudre ce problème, vous pouvez utiliser le mécanisme de travail Web . Dans ce cas, le schéma de travail avec les fonctions WASM "lourdes" peut ressembler à ceci:
- à partir du script principal d'un événement (par exemple, en cliquant sur un bouton) envoyer un message au travailleur avec la tâche de lancer une fonction lourde.
- , .
- - ()
WASM- JS, WASM . - ( ), HashMap , . ( JS) , / .
, Mutex , thread-safe. smart- . thread-safe Rc Arc RefCell RwLock . : 30%. --features=threaded thread-safe , WASM-.
6574 8098 ( 10 ):
, - 40..70% , , (32..37%) thread-safe ( cargo build --release --features=threaded ).
Firefox 67.0 Chromium 74.0.
WASM- ( ). https://webpbn.com/ http://www.nonograms.org/
TODO
"" /, / .
, . "" , , . .
( , 3600 ). WASM , ( , (!) , , WASM). , , - , nonogrid .
. : , , WASM . , ( ) , JS , .
JS. backtrace, .
( TOML- )
Résumé
, (, , etc).
Rust 1-3 PyPy 1.5-2 ( ).
Python Rust , Python (, , comprehensions), Rust-.
Rust WebAssembly . Rust , WASM, ( 1.5 ).
- The 'pbnsolve' Paint-by-Number Puzzle Solver by Jan Wolter and the survey
- The BGU Nonograms Project
- Solving Nonograms by combining relaxations
- An Efficient Approach to Solving Nonograms
- Color and black and white Japanese crosswords on-line
- 'Nonolib' library by Dr. Steven Simpson
- Rust and WebAssembly